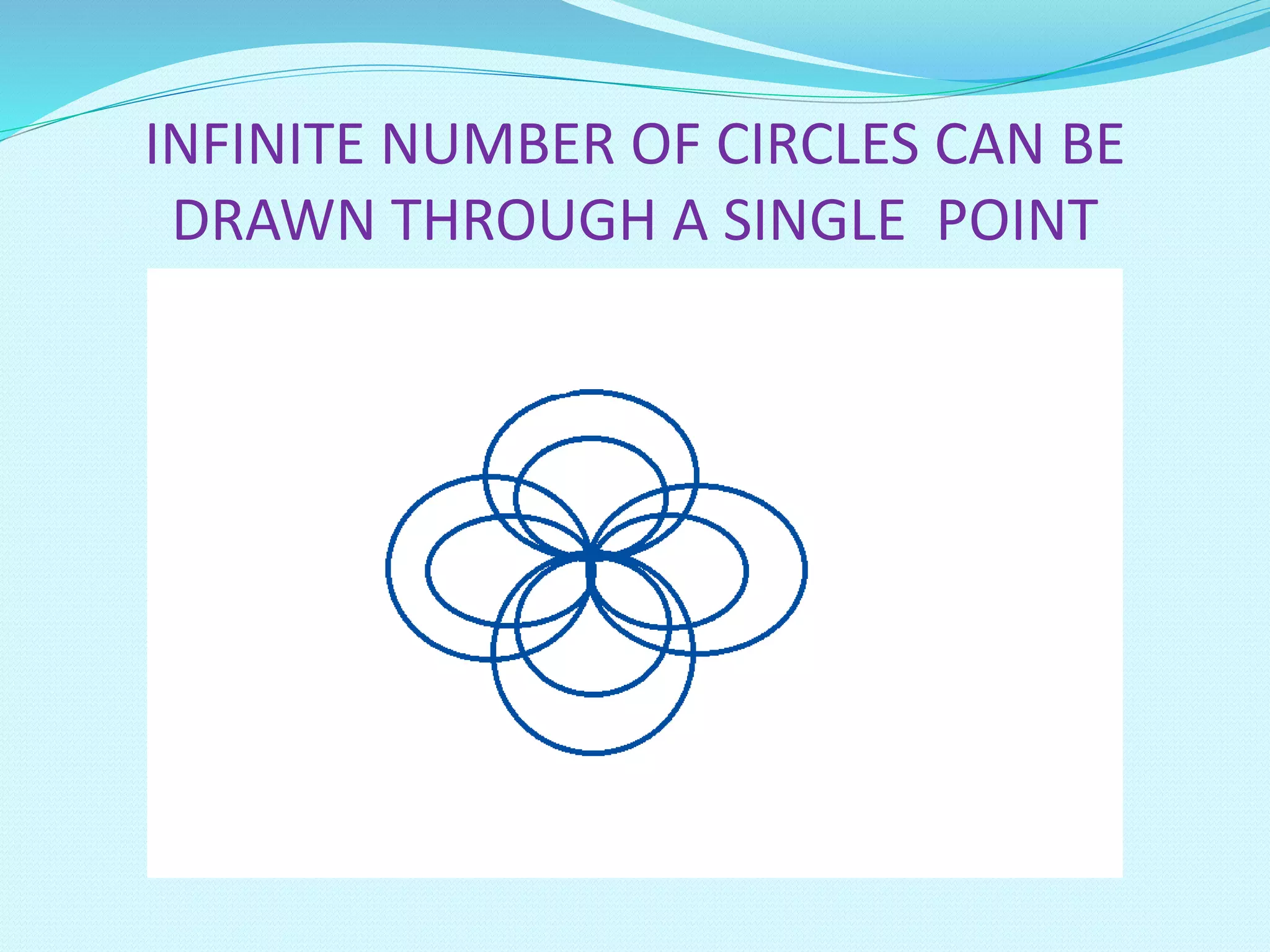
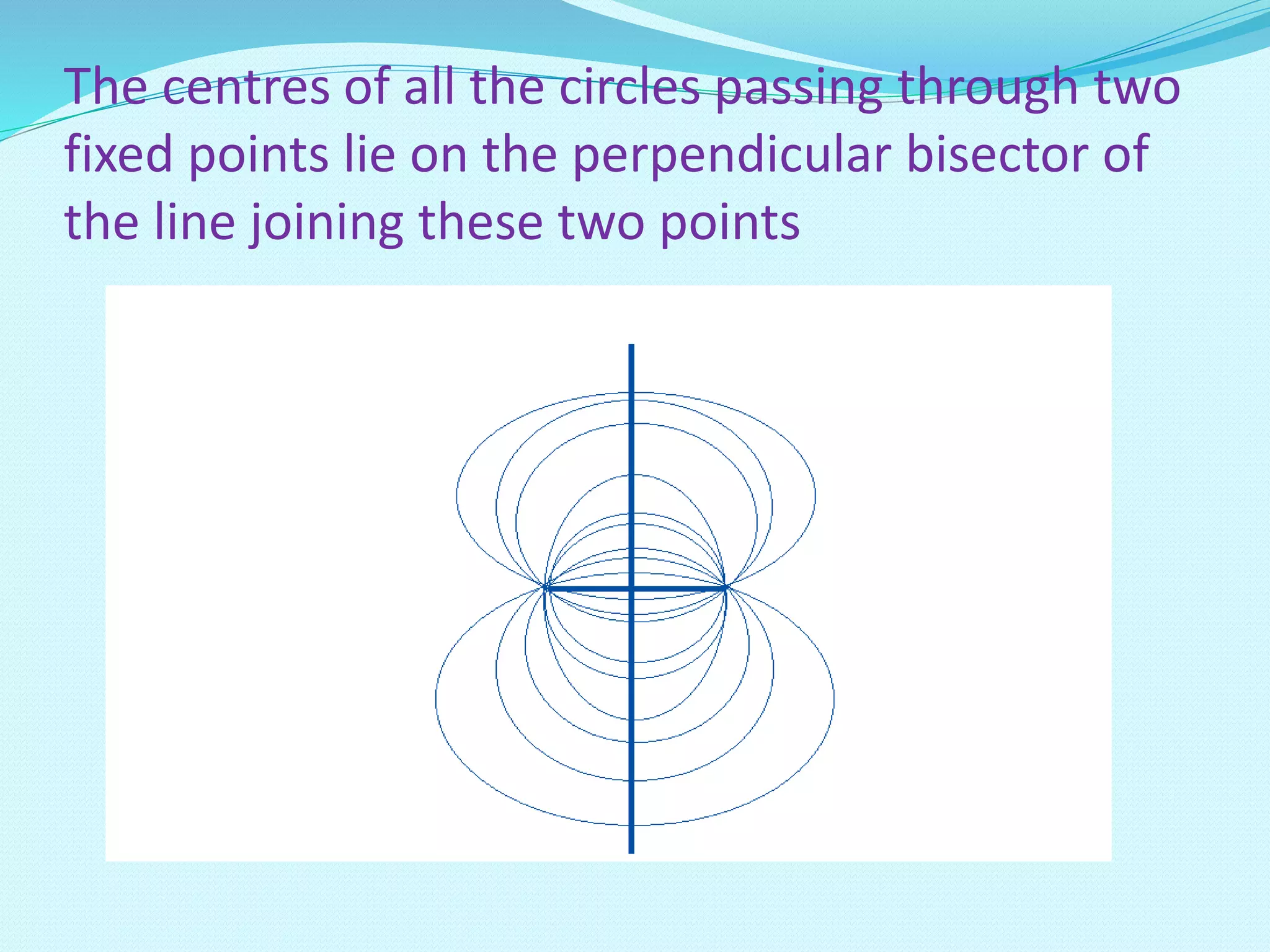
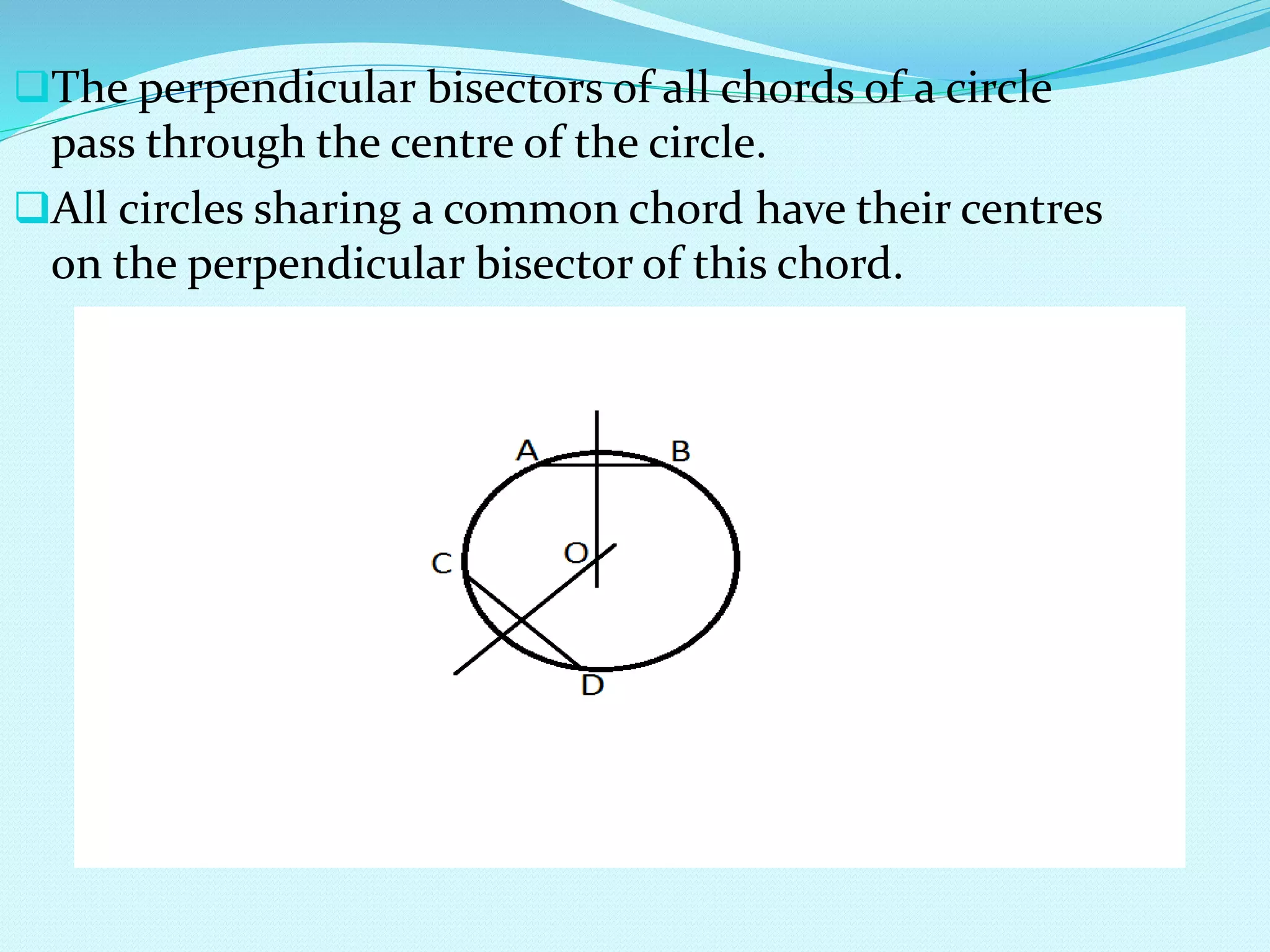
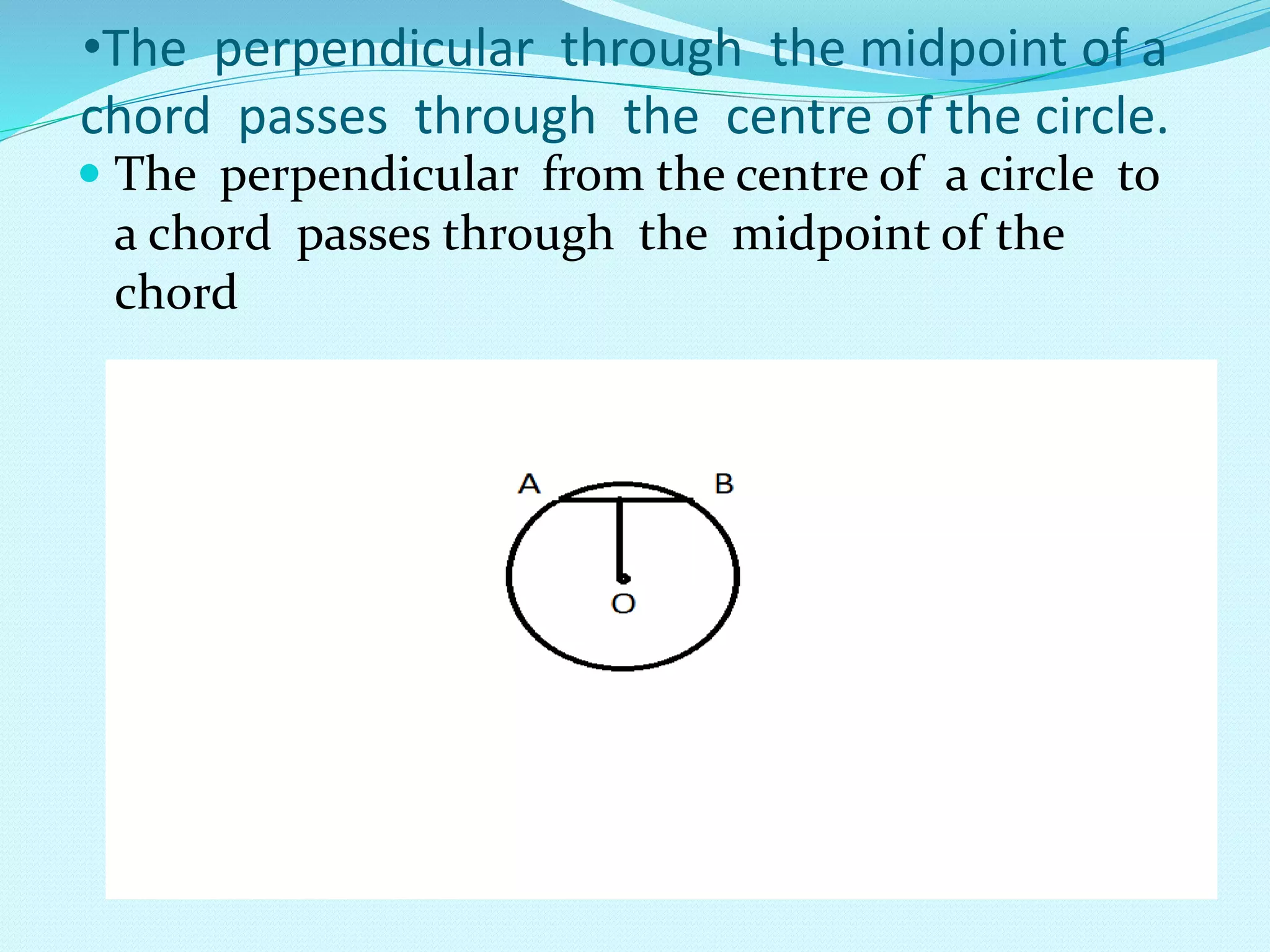
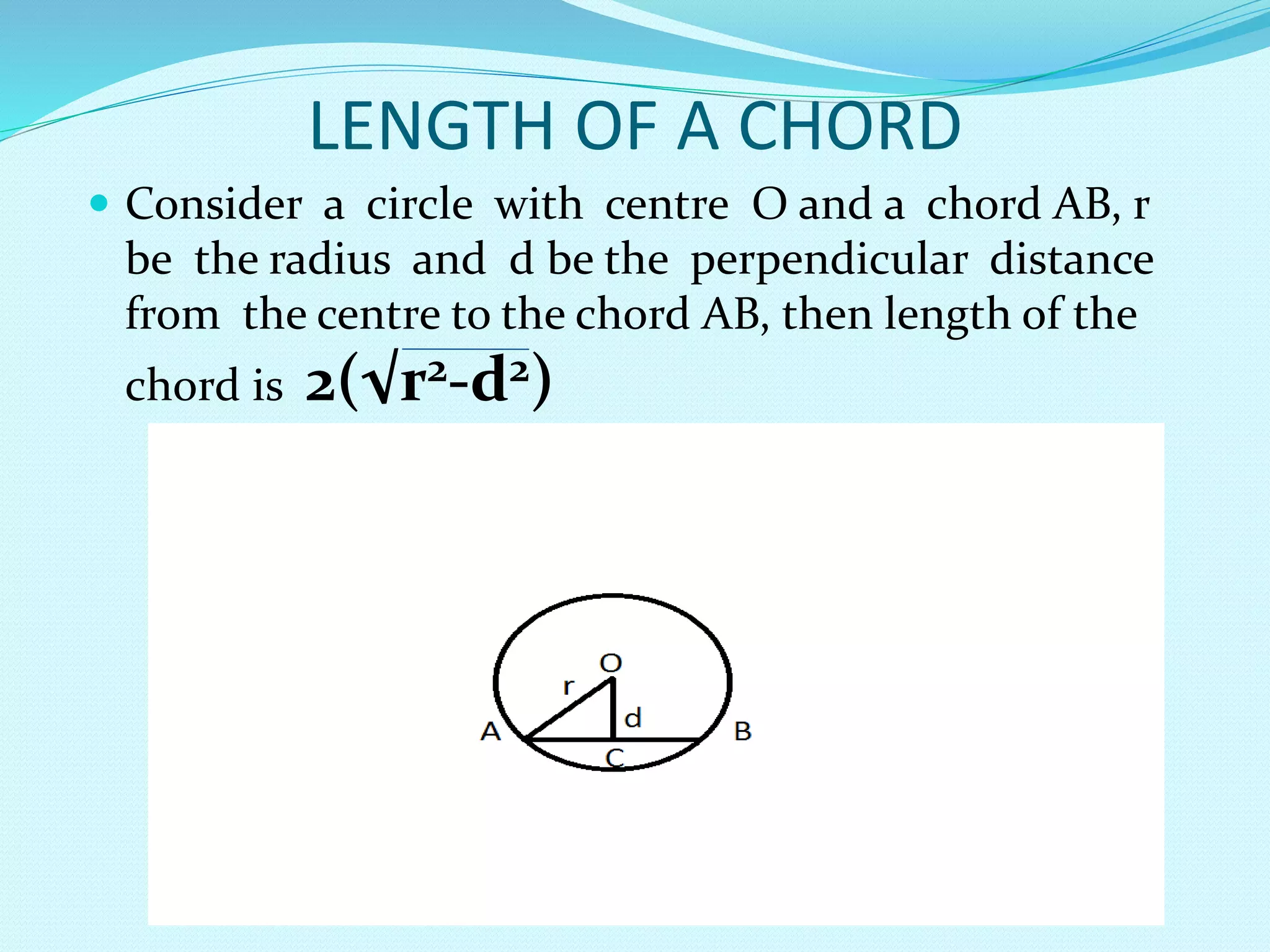
An infinite number of circles can be drawn through a single point. The centers of these circles all lie on the perpendicular bisector of the line connecting the two points. Additionally, the perpendicular bisectors of all chords of a circle pass through the center of the circle, and all circles sharing a common chord have centers on the perpendicular bisector of that chord. The document also discusses properties relating the length of a chord to the radius and distance from the center, as well as defining the circumcircle of a triangle.

2. INFINITE NUMBER OF CIRCLES CAN BE
DRAWN THROUGH A SINGLE POINT

3. The centres of all the circles passing through two
fixed points lie on the perpendicular bisector of
the line joining these two points

4. The perpendicular bisectors of all chords of a circle
pass through the centre of the circle.
All circles sharing a common chord have their centres
on the perpendicular bisector of this chord.

5. •The perpendicular through the midpoint of a
chord passes through the centre of the circle.
 The perpendicular from the centre of a circle to
a chord passes through the midpoint of the
chord

6. LENGTH OF A CHORD
 Consider a circle with centre O and a chord AB, r
be the radius and d be the perpendicular distance
from the centre to the chord AB, then length of the
chord is 2(√r2-d2)

7. CIRCUMCIRCLE
 The circle which passes through all the three vertices
of a triangle is known as the circumcircle.
 The centre of the circumcircle is the circumcentre
and radius of the circumcircle is the circumradius.

8. THANK YOU