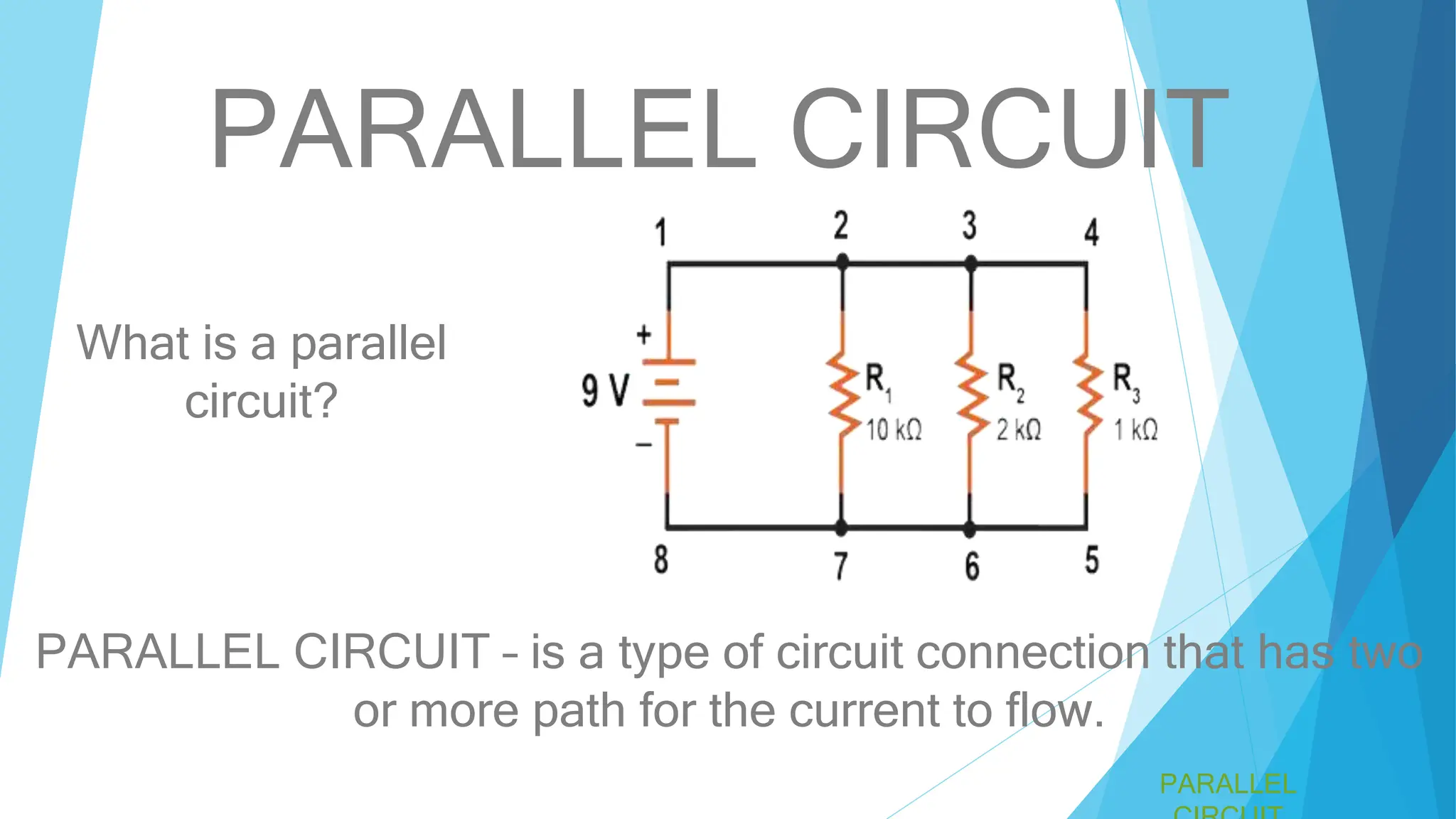
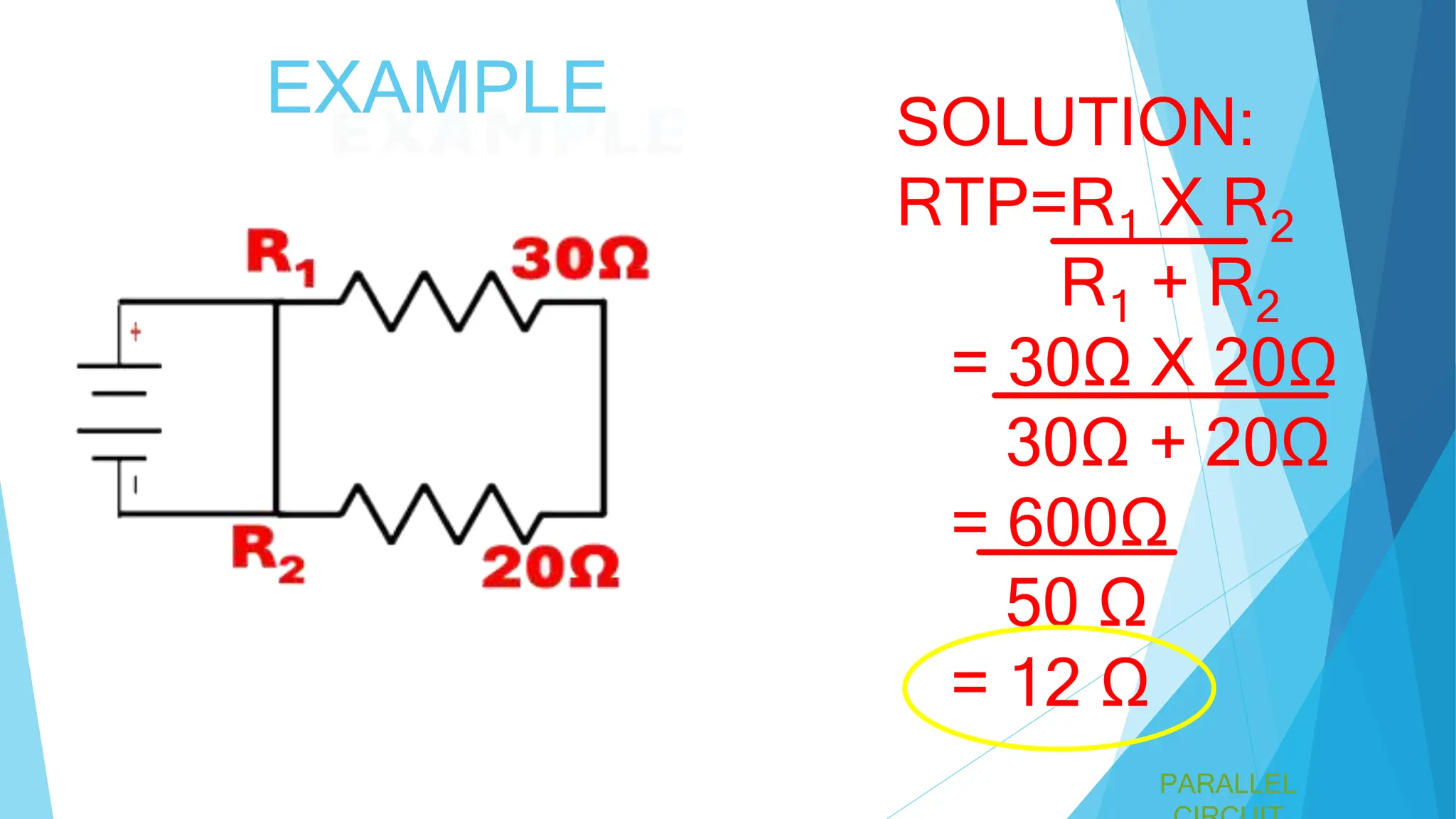
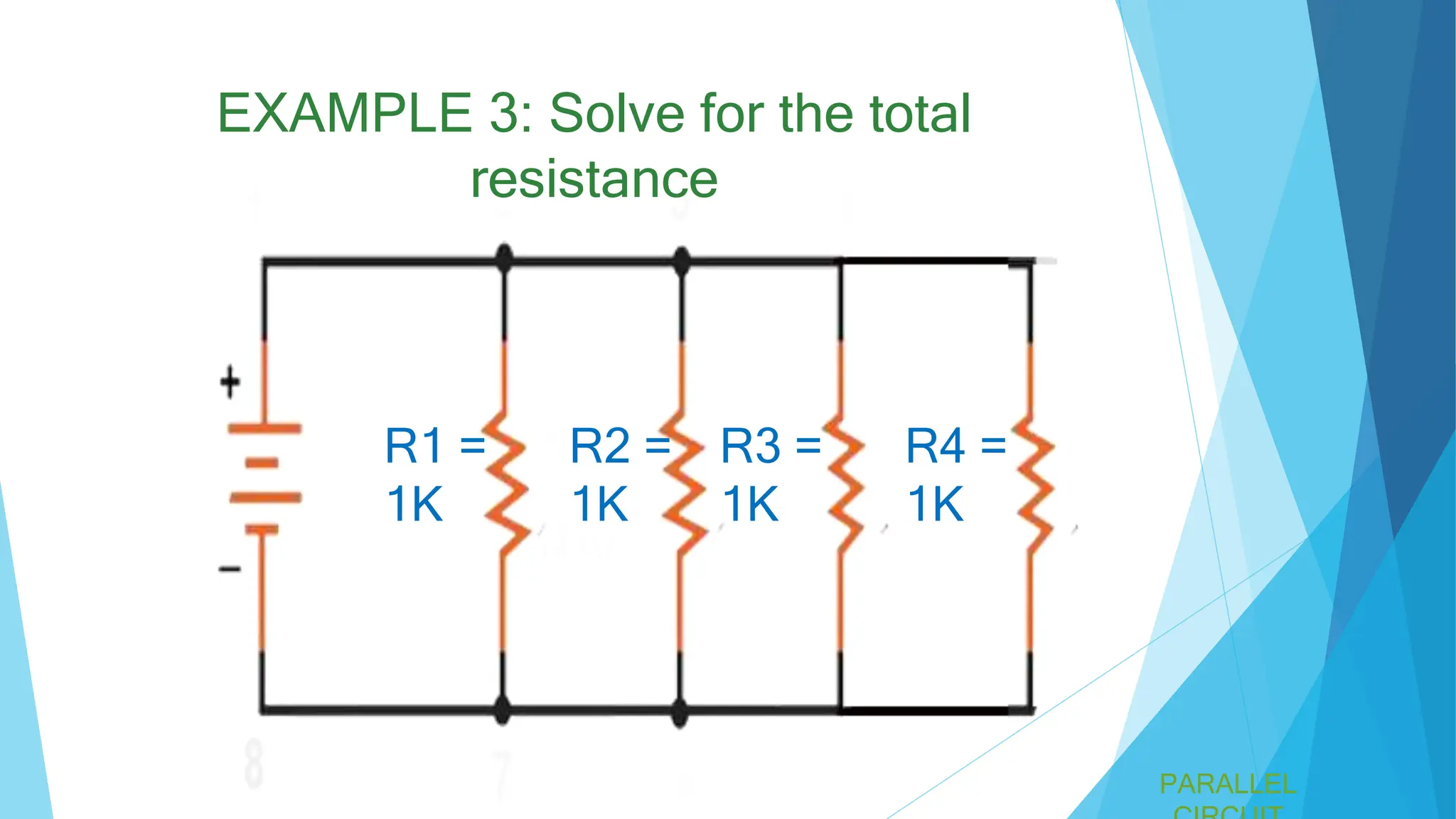
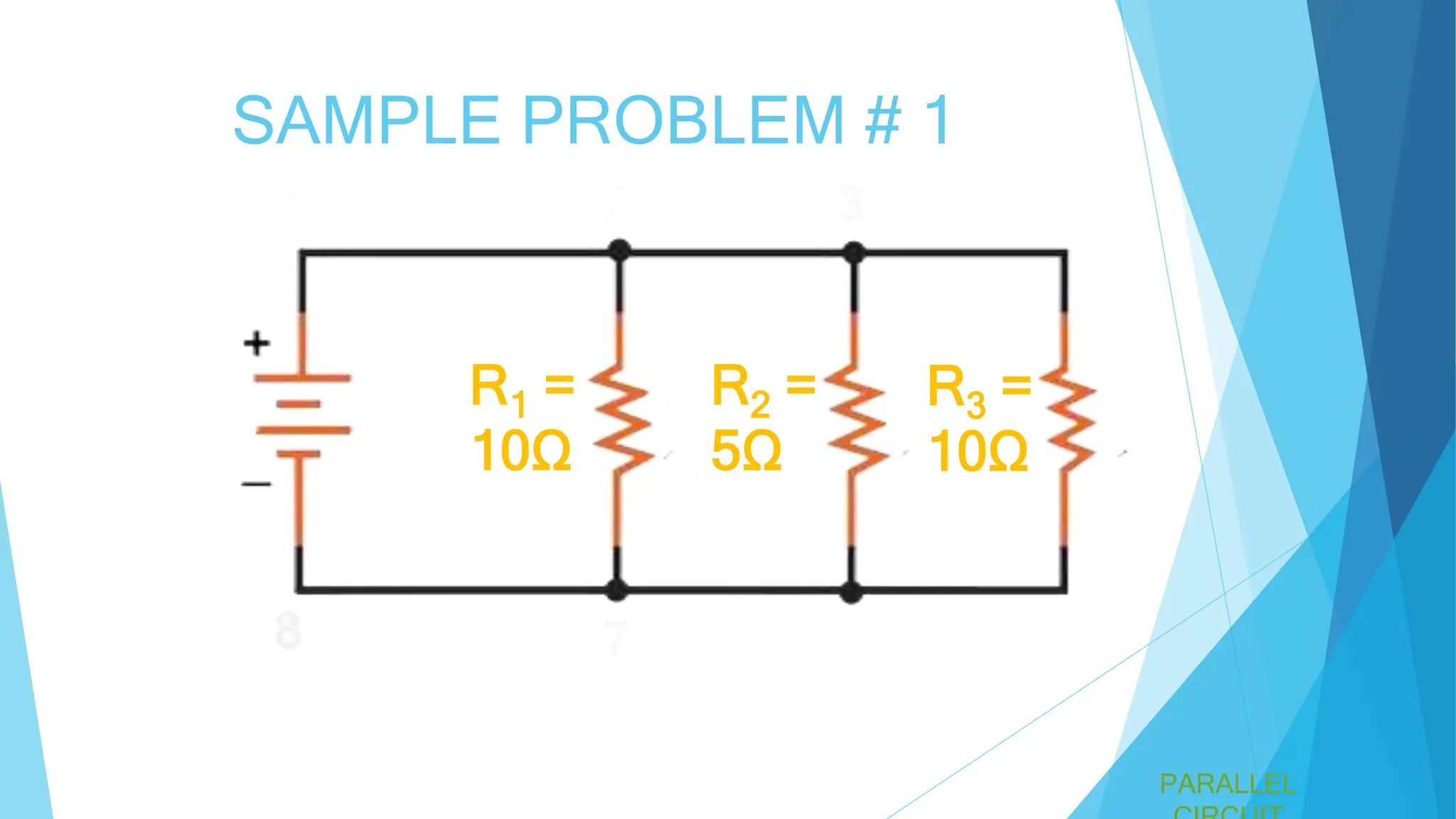
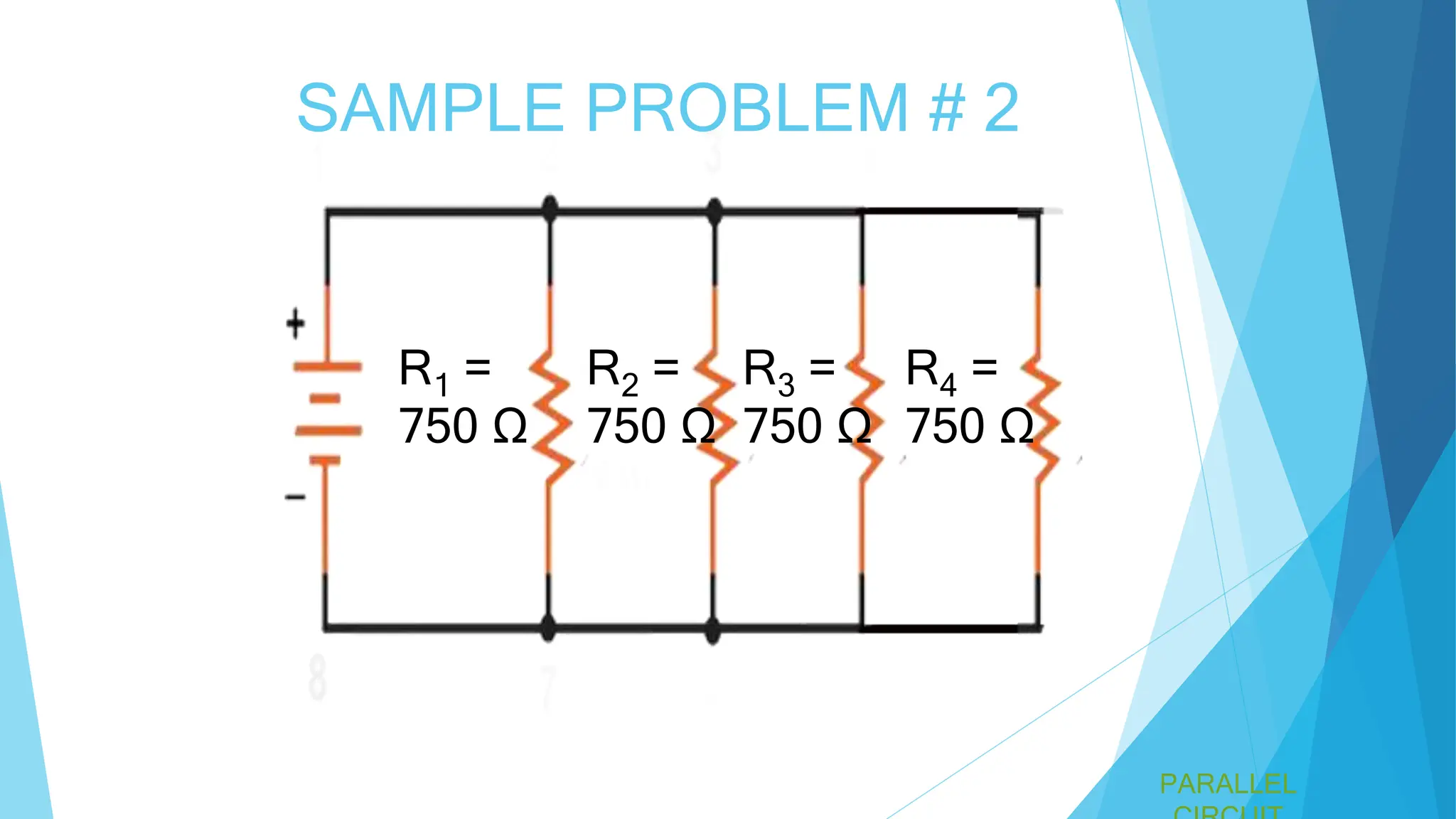
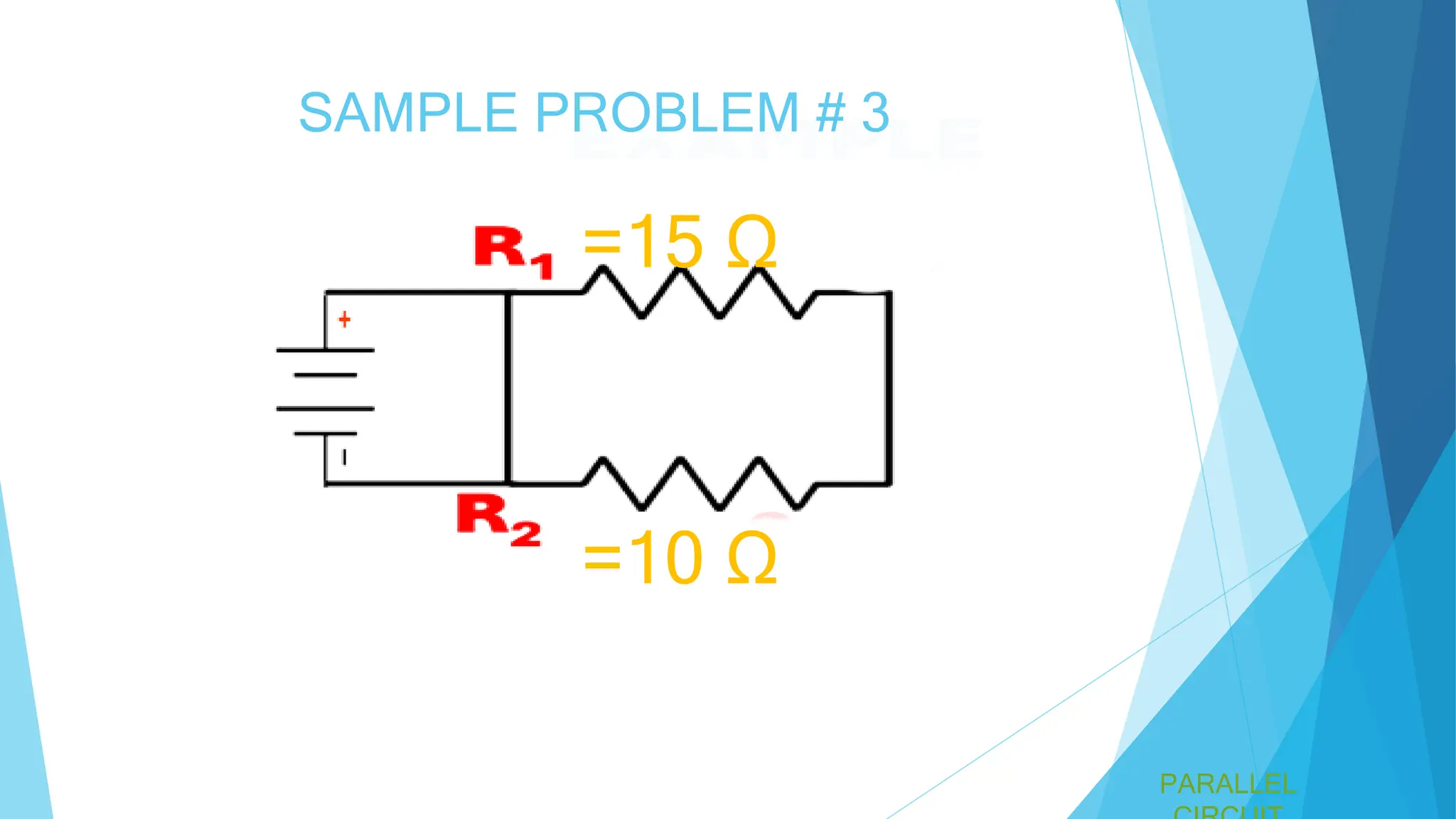
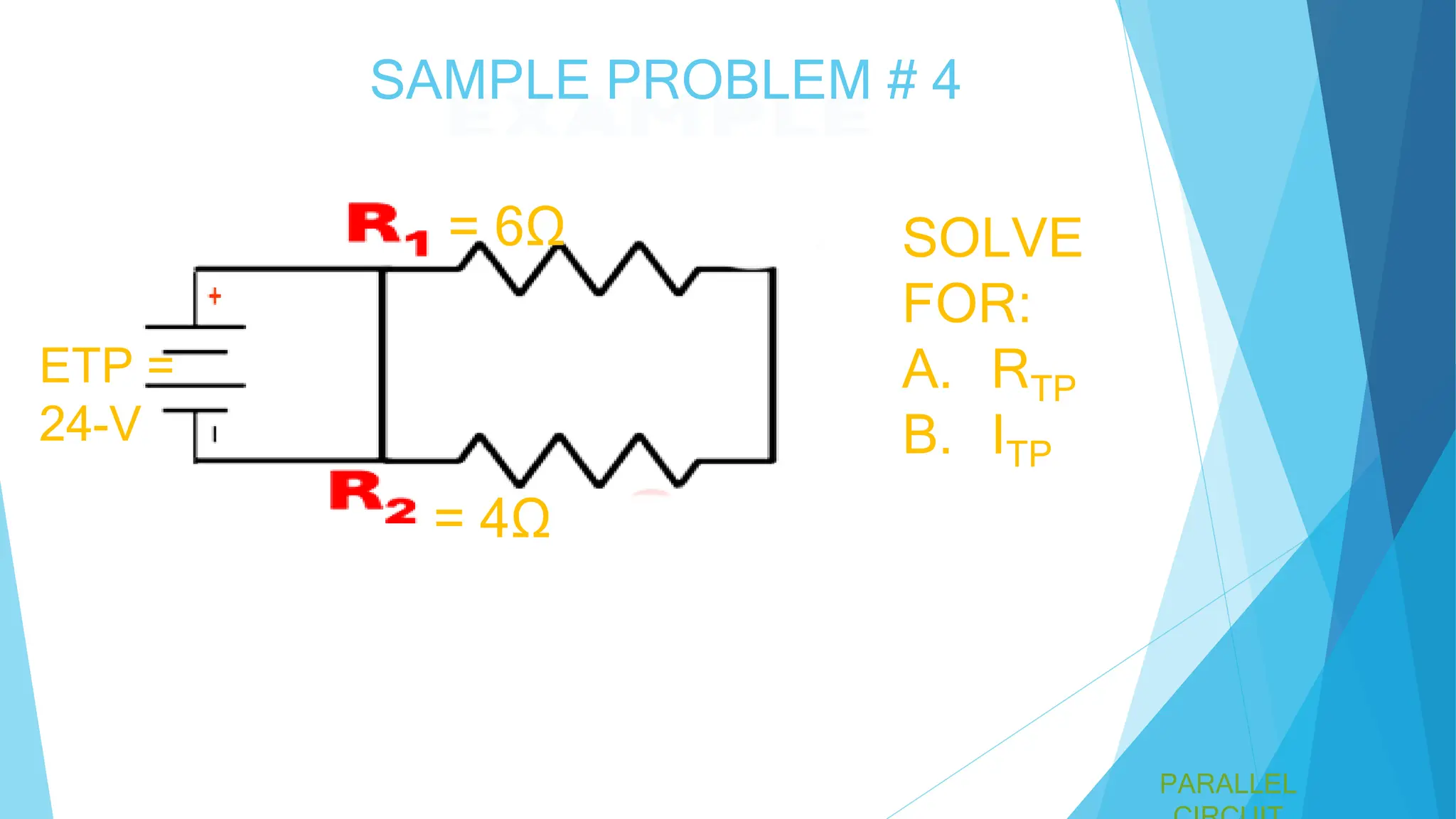
A parallel circuit involves multiple paths for current, with all components operating at the same voltage. The total current is the sum of the currents through each component, and the total resistance is less than the smallest individual resistance. Specific formulas and examples, including calculations for total resistance in various configurations, are provided.

1. PARALLEL CIRCUIT
PARALLEL
PARALLEL CIRCUIT – is a type of circuit connection that has two
or more path for the current to flow.
What is a parallel
circuit?

2. VOLTAGE
All components in parallel circuits operates at
the same voltage, it is expressed by the
following equation.
ETP=E1 =E2 =E3 =EN
Where:
ETP=total voltage in parallel
E1 =E2 =E3 =voltage across each resistor
EN=voltage drop at the last resistor
PARALLEL

3. PARALLEL
CURRENT
The components in a parallel circuit operates independently from one
another. Each component takes current in accordance with each
resistance. The number of separate path for current is equal to the
number of component in parallel. The total current in parallel circuit is
equal to the sum of the currents in parallel components.
ITP=I1 + I2 + I3 + IN
Where:
ITP=total current in parallel
I1, I2, I3 =current passing each resistor
IN=current passing at the last resistor

4. PARALLEL
RESISTANCE
The total resistance in parallel resistors is lower
than the lowest value of any individual resistor.
RTP=---------------
Where:
RTP=total resistance in parallel
R1 & R2 =value of individual resistor

R1 x R2
R1 + R2
Set A
Total
Resistance
of two
parallel
resistors

5. PARALLEL
EXAMPLE SOLUTION:
RTP=R1 X R2
R1 + R2
= 30Ω X 20Ω
30Ω + 20Ω
= 600Ω
50 Ω
= 12 Ω

6. PARALLEL
RESISTANCE: Set B
Total Resistance of two or more parallel resistors with
different value.
=
Where:
RTP= total resistance in parallel
R1, R2 & R3 = value of individual
resistor
Rn = value at the last resisor
+
1
____
_
RTP
1
___
R1
1
___
R2
1
___
R3
+ +
1
___
Rn

7. EXAMPLE 2: Solve for
the total resistance
R1 =
10Ω
R2 =
20Ω
R3 =
30Ω
PARALLEL

8. PARALLEL
SOLUTION:
1
---
RTP
=
1
---
10Ω
1
---
20Ω
+ +
1
---
30Ω
1
---
RTP
=
6 + 3 + 2
----------
60
1
---
RTP
=
11
---
60
11RTP
= 60
RTP =
60
---
11
RTP = 5.45Ω

9. PARALLEL
RESISTANCE: Set C
Total Resistance of two or more parallel resistors with
the same value.
R1
RTP = -----
RN
Where:
RTP=total resistance in parallel
R1 =value of resistors
Rn = number of resistors connected in parallel

10. EXAMPLE 3: Solve for the total
resistance
PARALLEL
R1 =
1K
R2 =
1K
R3 =
1K
R4 =
1K

11. SOLUTION:
PARALLEL
RTP =
R1
----
Rn
=
1000
------
4
= 250Ω

12. SUMMARY
VOLTAGE: ETP = E1 = E2 = E3 = . .
. En
CURRENT: ITP = I1 + I2 + I3 + In
RESISTANCE:
PARALLEL
R1 x R2
---------
R1 +
R2
RTP=
A: B:
1
----
RTP
=
1
----
R1
+
1
----
R2
+
1
----
R3
+
1
----
Rn
C: RTP=
R1
------
Rn

13. SAMPLE PROBLEM # 1
R1 =
10Ω
R2 =
5Ω
R3 =
10Ω
PARALLEL

14. PARALLEL
SOLUTION:
1
---
RTP
=
1
---
10Ω
1
---
5Ω
+ +
1
---
10Ω
1
---
RTP
=
1 + 2 + 1
----------
10
1
---
RTP
=
4
---
10
4RTP
= 10
RTP =
10
---
4
RTP = 2.5Ω

15. PARALLEL
SAMPLE PROBLEM # 2
R1 =
750 Ω
R2 =
750 Ω
R3 =
750 Ω
R4 =
750 Ω

16. SOLUTION:
PARALLEL
RTP =
R1
----
Rn
=
750 Ω
------
4
= 187.5Ω

17. SAMPLE PROBLEM # 3
PARALLEL
=15 Ω
=10 Ω

18. SOLUTION: RT
P
=
R1 x R2
-------------
R1 + R2
=
10 Ω x 15 Ω
-------------
10 Ω + 15
Ω
=
150 Ω
--------
25 Ω
= 6 Ω
PARALLEL

19. PARALLEL
SAMPLE PROBLEM # 4
ETP =
24-V
= 6Ω
= 4Ω
SOLVE
FOR:
A. RTP
B. ITP

20. SOLUTION:
PARALLEL
A. RTP =
R1 x R2
-------
R1 + R2
=
6 x 4
-------
6 + 4
=
24
-------
10
=2.4Ω
B. ITP =
ETP
----
RTP
=
24-V
-------
2.4 Ω
= 10A

21. SELF - CHECK
PARALLEL
1. FOUR 12Ω RESISTORS ARE CONNECTED IN
PARALLEL. CALCULATE THE TOTAL CIRCUIT
RESISTANCE.
2. FOUR RESISTORS CONNECTED IN PARALLEL. THE
RESISTANCE VALUES ARE 4 Ω, 8 Ω, 12 Ω & 16 Ω.
CALCULATE THE TOTAL CIRCUIT RESISTANCE.
3. DETERMINE THE TOTAL RESISTANCE OF A 10 Ω & 30
Ω RESISTORS CONNECTED IN PARALLEL.