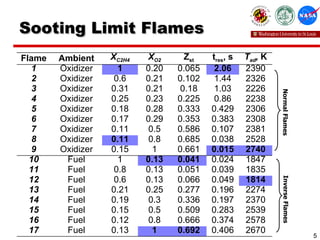
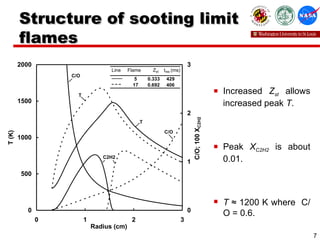
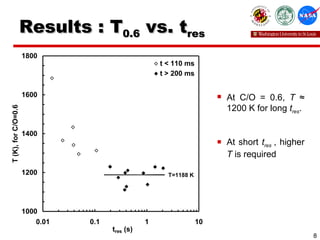
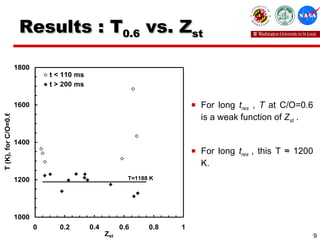
This study investigated the sooting limits of spherical diffusion flames of ethylene fuel in microgravity conditions. Numerical simulations using detailed chemistry models were performed to analyze the effects of local carbon-to-oxygen ratio, temperature, and residence time on 17 limit flames identified in previous experiments. The results show that for flames with residence times over 0.2 seconds, the critical temperature for sooting at a carbon-to-oxygen ratio of 0.6 is approximately 1200K, regardless of strain rate. For very short residence times under 0.1 seconds, higher temperatures are required at this carbon-to-oxygen ratio for sooting to occur.

1. A computational investigation of sooting limits of spherical diffusion flames V.R. Lecoustre 1 , B.H. Chao 2 , P.B. Sunderland 1 , D.L. Urban 3 , D.P. Stocker 3 , R.L. Axelbaum 4 1 University of Maryland, College Park, MD ; 2 University of Hawaii, Honolulu, HI ; 3 NASA Glenn Research Center, Cleveland, OH ; 4 Washington University, St. Louis, MO This work was supported by NASA. We thank S.A. Skeen for helpful discussions . 5 th U.S. National Combustion Meeting March 27, 2007

2. Background The critical soot formation T is 1250 – 1650 K (Glassman, 1998) in diffusion flames. Short t res can prevent soot formation. Microgravity offers strain-free 1D diffusion flames (Law, Axelbaum, Atreya, co-workers). 17 sooting limit microgravity flames were identified by Sunderland et al. (2004). Experiments: local critical C/O ratio of about 0.6 has been identified for ethylene spherical diffusion flames. Agrees with the global C/O ratio for premixed flames (Haynes and Wagner, 1981, Glassman, 1988).

3. Objectives Investigate sooting limits of microgravity C 2 H 4 diffusion flames, focusing on the effects of: local C/O atom ratio, local T , t res This numerical investigation uses detailed chemistry to study flame structure.

4. Identification of Sooting Limits Tests performed in NASA Glenn 2.2 s drop tower. Fuel – C 2 H 4 oxidizer – O 2 diluent – N 2 d at 2 s – 20 - 40 mm (a) 18% C 2 H 4  27% O 2 (b) 18% C 2 H 4  28% O 2 30 mm (c) O 2  12% C 2 H 4 (d) O 2  13% C 2 H 4

5. Sooting Limit Flames 2670 0.406 0.692 1 0.13 Fuel 17 2578 0.374 0.666 0.8 0.12 Fuel 16 2539 0.283 0.509 0.5 0.15 Fuel 15 2370 0.197 0.336 0.3 0.19 Fuel 14 2274 0.196 0.277 0.25 0.21 Fuel 13 1814 0.049 0.066 0.13 0.6 Fuel 12 1835 0.039 0.051 0.13 0.8 Fuel 11 1847 0.024 0.041 0.13 1 Fuel 10 2740 0.015 0.661 1 0.15 Oxidizer 9 2528 0.038 0.685 0.8 0.11 Oxidizer 8 2381 0.107 0.586 0.5 0.11 Oxidizer 7 2308 0.383 0.353 0.29 0.17 Oxidizer 6 2306 0.429 0.333 0.28 0.18 Oxidizer 5 2238 0.86 0.225 0.23 0.25 Oxidizer 4 2226 1.03 0.18 0.21 0.31 Oxidizer 3 2326 1.44 0.102 0.21 0.6 Oxidizer 2 2390 2.06 0.065 0.20 1 Oxidizer 1 T ad , K t res , s Z st X O2 X C2H4 Ambient Flame Normal Flames Inverse Flames

6. Numerical methods Sandia’s PREMIX code was modified to model steady-state or transient solutions of spherical laminar diffusion flames. Detailed chemistry (GRI Mech. 3.0, 53 species, 325 reactions) and transport properties were used. Optically thick radiation modeled. Ignition was via a steady state solution for a small domain (~1.2 cm) with adiabatic boundaries (Tse et al., 2001). At time zero, the transient computation commenced over an extended domain (100 cm) with radiation.

7. Structure of sooting limit flames Increased Z st allows increased peak T . Peak X C2H2 is about 0.01. T ≈ 1200 K where C/O = 0.6.

8. Results : T 0.6 vs. t res At C/O = 0.6, T ≈ 1200 K for long t res . At short t res , higher T is required

9. Results : T 0.6 vs. Z st For long t res , T at C/O=0.6 is a weak function of Z st . For long t res , this T ≈ 1200 K.

10. Conclusions Sooting-limit diffusion flames with t res > 0.2 s have T ≈ 1200 K where C/O=0.6, independent of Z st . Flames with t res < 0.1 s require increased T at this location. X C2H2 is a reasonable surrogate for soot precursors here. Peak X C2H2 ≈ 0.01 is predicted at the sooting limits.