Документ представляет собой дидактические материалы по алгебре и началам анализа для 9 класса, созданные для учителей и рекомендованные Министерством просвещения СССР. Он содержит самостоятельные и контрольные работы, а также материалы для итогового повторения, направленные на повышение уровня математической грамотности учащихся. В конце пособия представлены ответы на большинство заданий и рекомендации для учителей.













![С—31
Исследуйте на возрастание (убывание) и экстремумы функцию
f ( x ) = ± - x — x3.
С -3 2
1. Исследуйте квадратичную функцию у — З а
стройте ее график.
2. Решите неравенство:
Юлг-ЬЗ и по-
а) х2— 17л:— 1 8 ^ 0 ; б) 9л:2— 12х + 4 > 0 .
С -3 3
Исследуйте функцию
г / 2х—3 1
f M - 2 + х 1
и постройте ее график.
С—34
1. Найдите наибольшее и наименьшее значения функции
II
1
00
Xю
на отрезке [— 1; 2].
2. Разбейте число 10 на два неотрицательных слагаемых так,
чтобы сумма квадратов этих слагаемых была наименьшей.
С -3 5
1. Проверьте, является ли функция у — s i n решением диф
ференциального уравнения у" = — —•у.
2. Напишите дифференциальное уравнение гармонического
колебания у — 2 cos (х —л). Чему равны амплитуда, частота и на
чальная фаза этого колебания?
12](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-14-320.jpg)

![Найдите производную функции: а) 2x6+ 20y*; б) x c tg * ;
в) tg у -; г) cos х2', д) у —-р-.
С -4 0
С - 4 1
1. Найдите тангенс угла наклона касательной к графику функ
ции / (*)=cos (лг+ З) в точке с абсциссой х — — 3.
2. Вычислите приближенно:
а) 1,000000730°; б) sin ^ , считая я «3,1416.
С— 42
1. Исследуйте функцию f (х) = х3-~3х — 5 и постройте ее
график.
2. Найдите наибольшее и наименьшее значения функции
у = 4 х + — на отрезке [0,5; 4].
3. Материальная точка массой 3 кг движется по прямой
согласно уравнению s (<)= 2/3—2/ + 3 (s измеряется в метрах,
t — в секундах). Найдите действующую на нее силу в момент
времени / = 5 с.
Вариант 2
С — 1
1. Выразите в радианной мере величины углов 75° и 168°.
5зх 17я
2. Выразите в градусной мере величины углов у и — .
3. С помощью таблиц или калькулятора найдите радианную
меру угла:
а) 31°; б) 86°23'.
Найдите значения синуса и косинуса этих углов.
4. С помощью таблиц или калькулятора найдите градусную
меру угла:
а) 0,5400; б) 1,4327.
14](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-16-320.jpg)







![С—33
Исследуйте функцию
/ W - *+31— 2х
и постройте ее график.
С -3 4
1. Найдите наибольшее и наименьшее значения функции
у — 2х* —8х
на отрезке [—2; 1].
2. Разбейте число 18 на два неотрицательных слагаемых
так, чтобы произведение квадрата первого слагаемого и вто
рого слагаемого было бы наибольшим.
С—35
1. Проверьте, является ли функция y = sin 2х решением диф
ференциального уравнения у" = —2у.
2. Напишите дифференциальное уравнение гармонического
колебания у = 3 cos (х + я). Чему равны амплитуда, частота и
начальная фаза этого колебания?
С—36
1. Найдите tg ^ a + -j-^ , если известно, что c o s a = - ^ ,
0 < « < f .
2. Упростите выражение
sin a cos (я + «) cos (л — 2a)
cos 4a
3. Найдите без таблиц
sin 75° —sin 15°.
22](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-24-320.jpg)

![С—41
1. Найдите тангенс угла наклона касательной к графику функ
ции f (x)= sin (х — 3) в точке с абсциссой х0= 3.
2. Вычислите приближенно:
а) -/0>99999996; б) sin , считая я«3,1416.
С—42
1. Исследуйте функцию f(x)— x3—3x-j-5 и постройте ее
график.
2. Найдите наибольшее и наименьшее значения функции
4
У = х - - — на отрезке [1; 4].
3. Материальная точка массой 4 кг движется по прямой со
гласно уравнению s (t) = 3t + 2t3 (s измеряется в метрах, t — в
секундах). Найдите действующую силу в момент времени t = Зс.
Вариант 3
С -1
1. Выразите в радианной мере величины углов 64°, 160°.
2. Выразите в градусной мере величины углов l-j-я .
О 4
3. Отметьте на единичной окружности точку Р3п . Назовите
т
абсциссу и ординату этой точки, sin и cos .
С—2
1. Дано: sin а = —4~, 1 8 0 °< а < 2 7 0 °. Найдите cos а и ctg а.
5
2. Докажите тождество
16 sin4а — (sin2 а — 3 cos2 а)2 = 24 sin2 а — 9.
24](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-26-320.jpg)

![1. Вычислите:
a) sin (-1470°); б) cos (-6 9 0 °); в) tg (-1 3 2 0 °).
2. Упростите выражение
2 cos ^ cos а
cos (n + a )-sin 3^ - ^ - + a ^ — sin (л — a) cos3^ - ^ + a ^
С—8
С—9
Начертите график функции y = sinx на отрезке [—л; 2,5л].
Отметьте на этом графике множество точек, для которых выпол
няются условия: а) sin лг= 0,5; б) s in x = 'l; в) sin x > 0 ,5 . Вы
пишите соответствующие значения х, при которых выполняется
каждое из условий.
С—10
Начертите график функции у = cos х на отрезке [—л; 2,5л].
Отметьте на этом графике множество точек, для которых выпол
няются условия: а) cosx = 0,5; б) c o s x = l; в) c o sx > 0 ,5 . Вы
пишите соответствующие значения х, при которых выполняется
каждое из условий.
С—11
Начертите график функции y = t g x на отрезке [—л; 1,5л].
Отметьте на этом графике множество точек, для которых выпол
няются условия: а) t g x = l ; б) t g x < l . Выпишите соответ
ствующие значения х, при которых выполняется каждое из
условий.
С—12
Вычислите: а) ar csi n^— ; б) arctg УЗ;
в) sin^arccos^ —^ 0 ) ; г) tg ^ 2 arcsin^ •
26](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-28-320.jpg)


![С—24
1. Найдите область определения функции У ~ ^ 9Л ■
2. Найдите <р'(—•1), если ф (дс)= (5 + блс)1°.
С—25
1. Найдите производную функции:
а ) f (х) = 3 cos 2 л:; б ) <p (*) = 4 tg Зх.
Вычислите Г ( —у ) и <р'^
2. Решите уравнение g ' (х)=0, если g (x) = sin х + 0,5 sin 2х.
С—26
Решите неравенство:
a) - y f ,-— < 0 ; б) (х--2)-л]х2— 1> 0 .
С—27
Дана функция f (х)= — + + 4.
а) Составьте уравнение касательной к графику данной функ
ции в точке его с абсциссой хо= —2.
б) Выполните рисунок.
в) Вычислите площадь треугольника, ограниченного отрез
ками касательной и осей координат.
С—28
Вычислите приближенно:
а) Т48Д6; б) sin 1,03; в) cos 43°.
С—29
Основание параллелограмма а изменяется по закону а = 2 + 5/,
а высота b — по закону 6 = 2 + 6/. Вычислите скорость изменения
его площади в момент t — Зс. Основание а и высота b изме
ряются в сантиметрах.
29](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-31-320.jpg)
![Найдите промежутки возрастания и убывания функции:
а) / (х) — х2+ Зх 6; б) ф {х) = хъ+ 2 х — 1;
в) g (х)= х3— Злг2+ 5.
С—31
Исследуйте на максимум и минимум функцию:
a) f(x) = x* — 8х2; б) Ф( * )= - J - + i- .
С—32
Исследуйте функцию f ( х ) = —х2(х2—4) с помощью произ
водной и постройте ее график.
С—33
Исследуйте функцию f{x)— -^-x5— ?—х3 с помощью произ-
р О
водной и постройте ее график.
С—30
С—34
Найдите наибольшее и наименьшее значения функции
/ (x) = cos х — 5- cos Зл:
на отрезке
[ 0: т ] ■
С—35
1. Дана функция f (х) = 6 sin . Найдите f ' (х), f" (х),
f ' ( - n ) , f " ( f ) •
2. Напишите три отличных от нуля решения дифференциаль
ного уравнения у " = — 9у.
30](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-32-320.jpg)



![С—8
1. Вычислите:
a) sin (-1860°); б) cos (-4 2 0 °); в) ctg( —930°).
2. Упростите выражение
cos | | sin3 (л — а ) - -cos (л + а) sin3 1
(¥-•)2 sin a sin |
(т -“)1
С—9
Начертите график функции г/= sin л: на отрезке [—0,5л; Зл].
Отметьте на этом графике множество точек, для которых вы
полняются условия:
a) sin х = 0,5у/2; б) s in x = — 1; в) sinx> 0,5V 2.
Выпишите соответствующие значения х, при которых выпол
няется каждое из условий.
С—10
Начертите график функции у — cos х на отрезке [—0,5л; Зл].
Отметьте на этом графике множество точек, для которых выпол
няются условия:
a) cos х = 0,5у/3; б) c o s x = — 1; в) cos х>0,5-/3.
Выпишите соответствующие значения х, при которых выпол
няется каждое из условий.
С - 1 1
Начертите график функции у — tg х на отрезке [— 1,5л; л].
Отметьте на этом графике множество точек, для которых выпол
няются условия:
a ) tg х = — 1; б) t g x > — 1.
Выпишите соответствующие значения х, при которых выпол
няется каждое из условий.](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-36-320.jpg)













![1. Исследуйте квадратичную функцию и постройте ее график:
у = —0,5х2+ 2х + 2,5.
2. Решите неравенство:
а) Здс2—2х + 1> 0 ; б) 9х2- 18х + 4 < 5 х 2- 6 х + 11.
С—32
С— 33
Исследуйте функцию и постройте ее график:
у = хА~ 2 х 2~-1.
С -3 4
1. Найдите наибольшее и наименьшее значения функции
f (х)=Зх5- 5 х 3+
на отрезке [—2; 2].
2. Разбейте число 6 на два неотрицательных слагаемых так,
чтобы произведение квадрата первого слагаемого и второго
слагаемого было наибольшим.
С— 35
1. Проверьте, является ли функция jc(/) = sin5f решением
дифференциального уравнения х" ( t ) = —25x(t).
2. Запишите дифференциальное уравнение гармонического
колебания х (/) = 3 cos (-/2 t — 1). Укажите амплитуду, частоту
и начальную фазу этого колебания.
С—36
1. Найдите sin (а + Р), если известно, что sin а = ~ , —■< а < л;
О Z
cos р = g—, л < р < у - .
2. Упростите выражение
cos2( —- -2ос^ 2
V2 2 cos2 — 2 sin2-2-) .
cos2(л—а) ’ V 2 27
3. Найдите tg 22°30' и sin 22°30'.
48](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-50-320.jpg)

![1. Исследуйте функцию у = 4х — х4 и постройте ее график.
2. Найдите наибольшее и наименьшее значения функции
/ (x)=p-Ly на отрезке [— 1; 0,5].
С—42
Вариант 6
С -1
1. Выразите в радианной мере величины углов 42° и 130°.
2. Выразите в градусной мере величины углов - - и л.
3. С помощью таблиц или калькулятора найдите радианную
меру угла:
а) 57°; б) 88°55'.
Найдите значения синуса и косинуса этих углов.
4. С помощью таблиц или калькулятора найдите градусную
меру угла:
а) 0,8796; б) 2,3422.
С— 2
1. Докажите справедливость равенства
j . cos4 а + sin2 a cos2 а 1
sin2а ‘ sin2 а
2. Определите знак выражения:
„ч sin 110° cos 220° п i л
а) ~ctg 330° ; б> sin 2 -ctg 4.
3. Найдите sin а и ctg а, если известно, что t g a = 3 и а
не лежит в III четверти.
50](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-52-320.jpg)

![1. Докажите, что функция у = х3—Зх убывает на проме
жутке [— 1; 1].
2. Найдите нули функции у — —0,5х2+ 2л: и координаты ее
вершины. Начертите схематически график данной функции
и с его помощью найдите промежутки возрастания и убывания
этой функции.
С - 7
С— 8
1. Пользуясь периодичностью, четностью или нечетностью со
ответствующей тригонометрической функции, запишите данное
значение так, чтобы аргумент был выражен наименьшим положи
тельным числом градусов или радиан: a) sin 312° 19'; б) cos 5042°;
В) C t g f .
2. Вычислите cos (—30°) -f- sin 660° + ctg (—510°).
3. Найдите наименьший положительный период функции:
a) y = tg (1 —Зх); б) i/ = sin4x + cos4х.
С—9
1. Отметьте на единичной окружности множество точек Pt,
для которых соответствующие значения синуса удовлетворяют
неравенству sin / > 4 ~.
2. Найдите точки максимума и минимума функции / (*)=
= s in (2* + f ) .
3. Расположите в порядке убывания числа
sin (—300°); sin (—250°); sin (— 150°); sin 20°; sin 40°.
С— 10
1. Расположите в порядке возрастания числа
cos 10°; cos 70°; cos (—20°); sin 15°.
2. Отметьте на графике функции у — cos л: множество точек,
для которых соответствующие значения косинуса удовлетворяют
неравенству cos х > —
3. Найдите промежутки возрастания и убывания функции
» - « • ( ■ § — пг) ■
52](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-54-320.jpg)



![С—30
1. Найдите промежутки возрастания и убывания функции
f (х) = 2х3+ Зх2— 12х.
2. Найдите критические точки функции
f {х)=2х—л[х.
Укажите, какие из этих точек — точки максимума функции,
а какие — точки минимума.
С—31
Исследуйте на возрастание (убывание) и экстремумы функцию
f (х) = 2 х2—х4+ 3.
С—32
1. Исследуйте квадратичную функцию и постройте ее график:
у — —0,5х2+ * + 1,5.
2. Решите неравенство:
. а) 2х2- х + 1 < 0 ; б) 16x2+ 6* + 3 > 7 x 2- 6 x - 1.
С—33
Исследуйте функцию и постройте ее график:
у = 2 х 3—6х2+ 4.
С—34
1. Найдите наибольшее и наименьшее значения функции
f(x) = x* + 20х2+ 3
на отрезке [— 1; 1].
2. Разбейте число 8 на два неотрицательных слагаемых так,
чтобы сумма квадрата первого слагаемого и куба второго сла
гаемого была наименьшей.
57](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-59-320.jpg)

![С -3 9
1. Решите неравенство:
а) х2—6х + 8 > 0 ; б) х2— 12х + 3 6 < 0 .
2. Решите неравенство методом интервалов:
а) (X—1)-(х+ 2 ) ^ 0. б)
х—3 х —j~I х“I-2
С— 40
Найдите производную функции:
а) х7—2х?+ 3 х —3; б) (1+Зх)н/х; в) cos 5х;
г) ctg (y -x + 5) ; д) ( j-x —б)
С— 41
1. Напишите уравнение касательной к графику функции
/ (х) = Зх + 2х2 в точке с абсциссой хо=1.
2. Вычислите приближенно:
а) д/Ь002; б) 0,9999760.
3. Материальная точка движется по прямой согласно уравне
нию
* (0 = * 3+ y * * - 7 f .
Найдите ее скорость и ускорение в момент времени to— 2>.
С— 42
„4
1. Исследуйте функцию у = 8х — — и постройте ее график.
2. Найдите наибольшее и наименьшее значения функции
f (х)— -гт~г на отрезке [—2; 0,5].X -р 1
59](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-61-320.jpg)







![С—34
1. Найдите наибольшее и наименьшее значения функции
f(x) = x3- 2 x 2+ 8 x - 2
на отрезке [—4; 2].
2. В прямоугольный треугольник с гипотенузой 16 см и углом
60° вписан прямоугольник, основание которого лежит на гипоте
нузе. Каковы должны быть размеры прямоугольника, чтобы его
площадь была наибольшей?
С— 35
1. Запишите общий вид решений для дифференциального
уравнения
и " = - и -
2. Напишите дифференциальное уравнение гармонического ко
лебания x(t) = 2 sin Укажите амплитуду, частоту и начальную
фазу этого колебания.
С— 36
5
1. Найдите cos (а + (5), если известно, что cos а = -у,
• л 1 2 /~ . ЗХ ЗХ________
_
о
Р=ТГ' 0 < а < — , у < Р < л .
2. Упростите выражение
8 sin2(л —a) sin2^ y - |- a ) — 1.
3. Найдите sin у - и tg ~ если c o s a = — 0 < а < л .
С— 37
Проведите исследование и постройте график функции:
а) f(x) = cos(^2x— у ) ; б) f ( x ) = y + s i n в) f(x) = 3-
3* 67](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-69-320.jpg)

![С—42
1. Исследуйте функцию f ( x ) = x 4— 8x2 и постройте ее график.
2. Найдите наибольшее и наименьшее значения функции
/ (х) —2 л:3 + Зх2+ 2 на отрезке [—2; 0].
Вариант 8
С— 1
1. Выразите в радианной мере величины углов 48° и 188°.
2. Выразите в градусной мере величины углов ^ и ^-п.
3. С помощью таблиц или калькулятора найдите радианную
меру угла:
а) 23,6°; б) 83°53'.
Найдите значения синуса и косинуса этих углов.
4. С помощью таблиц или калькулятора найдите градусную
меру угла:
а) 0,0995; б) 3,1012.
, „ С— 2
1. Докажите справедливость равенства
sin2 а (1 -f-sin-1 a + ctg а) (1 —sin-1 а -f-ctg а) = 2 sin а cos а.
2. Определите знак выражения:
ч sin 200° cos 20° 1 • о * с
а ) Tg 3 0 0 ° c tg ib 0 ° ; б > cos sin 3 tg 5.
3. Найдите sin а и cos а, если известно, что tgoc = 3 и а не
лежит в I четверти.
1. Вычислите: С—3
a) sin 1935°; б) tg 1395°; в) c o s ^ .
2. Упростите выражение (cos 70° + cos 50°) (cos 310° +
+ cos 290°) + (cos 4 0 ° + cos 160°) (cos 320° —cos 380°).
3. Докажите тождество
tg ( л - а ) ( 1 + t g ( § 4 -a) c t g ( f - + 2a )) = tg (2л - a ) -
- c t g ( | - - 2a) .
69](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-71-320.jpg)






![С—30
1. Найдите промежутки возрастания и убывания функции
/ (х)— х3--Зх—8.
2. Найдите критические точки функции
Укажите, какие из этих точек — точки максимума функции,
а какие — точки минимума.
С—31
Исследуйте на возрастание (убывание) и экстремумы функ
цию
f W = (7 ^ 3 f-
С—32
1. Исследуйте квадратичную функцию и постройте ее график:
f (х)— 3х2— 4х — 7.
2. Решите неравенство:
а) х2— 9х — 2 2 ^ 0 ; б) х2--8х-- 16 > 0 .
С—33
Исследуйте функцию и постройте ее график:
I W x 2 _ i_ g •
С—34
1. Найдите наибольшее и наименьшее значения функции
f (х)= х3—2х2+ 8х —-2
на отрезке [1; 4].
2. В прямоугольный треугольник с катетом 12 см и про
тиволежащим углом 30° вписан прямоугольник, основание ко
торого лежит на гипотенузе. Каковы должны быть размеры
прямоугольника, чтобы его площадь была наибольшей?
76](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-78-320.jpg)

![С—39
1. Решите неравенство:
а) х2—Ъх —7 < 0 ; б) *2+ 6* + 9 > 0 .
2. Решите неравенство методом интервалов:
а ( * — (ЛГ+ 3 ) 8 A . g 5 . 6 о
а) зТ+Т ^ и’ ' зГГГ+ 2ГГТ< ’3-
С—40
Найдите производную функции:
а) Зх — 7x3+ - i- x 8+ *9; б) x ^ j5 + x ; в) cos 0,3л:;
г) c tg ( ^ — Зл:) ; д) (5*2— I)8.
С—41
1. Напишите уравнение касательной к графику функции
f (х) = х2— Зх — З в точке пересечения графика с осью ординат.
2. Вычислите приближенно:
а) -уд/0,999996 ; б) 0,99997350.
3. Материальная точка движется по прямой согласно урав
нению
Найдите ее скорость и ускорение в момент времени to==1.
С -4 2
1. Исследуйте функцию / (х) = 2х2— х4 и постройте ее график.
2. Найдите наибольшее и наименьшее значения функции
/ (л:)= 2 + 3х2—х3 на отрезке [—2; 2].
78](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-80-320.jpg)


![С — 8
1. На рисунке 7 приведена часть гра
фика периодической функции, имеющей
период Т. Продолжите график на отре
зок [—2Г; 3Т].
2. Найдите наименьший положитель
ный период функции:
а ) / (х) = Isinxl + tg 2х;
б) f (x) = cos(^j2 х — .
/1 1 Л ,
-т т 0
2
Т Т х
2
Рис. 7
3. Докажите,
= COS XCOS (■>/2х ) -
что функция: а) / (x) = sin х2; б) f (х) =
■не является периодической.
С—9
1. Отметьте на единичной окружности множество точек Р>,
для которых соответствующие значения синуса удовлетворяют
1 /о
неравенству у - < Isin /| •
2. Найдите область значений функции
f (х) = sin2х —2sin л:+ 3.
3. Определите знак числа (sin 2 —sin 4) (sin 3 —sin 5).
С—10
1. Отметьте на графике функции у = cos х множество точек,
для которых соответствующие значения косинуса удовлетво
ряют неравенству
Icos х | .
2. Пользуясь возрастанием (убыванием) функции y = sirix
{у — cos х) на отрезке J^O; -p-J , докажите, что
cos sin у - > sin cos ~ .
3. Найдите область определения функции
/ W = ----- 1— г -
cos22 х —
4
4 Заказ 68 81](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-83-320.jpg)








![1. Найдите область определения функции, заданной фор
мулой:
0,5х2~ х + 2 х 3 _________
a) f(x) = — — l — б) f (*)—д/3 Ал[х .
х (4 —л/х— 1)
2. Дана функция
{( ч / 2jc2+ 1 при |* |< 3 ,
IVе)— Зх —7 при х ^ 3 .
а) Вычислите /( —3), /(2), /(5), /(* 2+ 4).
б) Начертите график данной функции.
С—5
С— 6
1. Может ли уравнение f (х)— 0 иметь в точности 6 корней,
если / всюду определенная и: а) четная функция; б) нечетная
функция?
2. Докажите, что любая функция с симметричной относи
тельно точки О областью определения может быть представлена
в виде суммы четной и нечетной функций, причем единственным
образом.
С— 7
1. Найдите промежутки возрастания и убывания функции:
а) f {х) = Зх2—4л:+ 5;
б) ( W = T T ? -
2. Пусть функции / и g возрастают на всей числовой прямой.
Приведите примеры, показывающие, что функция / —g может:
а) возрастать на всей числовой прямой;
б) убывать на всей числовой прямой;
в) быть убывающей на (— оо; 0] и возрастающей на [0; оо);
г) иметь бесконечно много промежутков возрастания и убы
вания.
91](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-93-320.jpg)
![1. На рисунке 9 приведена
часть графика периодической
функции, имеющей период Т.
Продолжите график на отрезок
[ — ЗТ; 2Т].
2. Найдите наименьший по
ложительный период функции:
а) /( x ) = |c o s x |+ c tg y - ;
б) f(*) = sin(V 3*—f-)-
а) / W = sin д/|х|;
б) / (х) = cos х + cos д/2х — не является периодической.
С - 8
С - 9
1. Отметьте на единичной окружности множество точек Pt,
для которых соответствующие значения синуса удовлетворяют
неравенству -5- ^ Isin t ■< 1.
2. Найдите область значений функции
/ (х) = 5 —4 sin х —sin2х.
3. Определите знак числа (sin 2 —sin 1) (sin 4 —sin 3).
С—10
1. Отметьте на графике функции у = cos х множество точек,
для которых соответствующие значения косинуса удовлетво
ряют неравенству
|cos х < 1.
2. Пользуясь возрастанием (убыванием) функции у = sin х (у =
= cos х) на отрезке ^0; -|-j, докажите, что cos (sin l)> s in (cos 1).
3. Найдите область определения функции
/ М = — — - ■2 *COS^X——
'Т _ 2 Т Т 0
3 3
I 2 J т
J 3
Рис. 9
3. Докажите, что функция:
92](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-94-320.jpg)









![4. Исследуйте функцию / (х)= х3+ х и постройте эскиз ее
графика (без использования производной).
Опишите схему исследования функции.
5. Расположите в порядке возрастания числа sin 2, sin 4,
sin 6.
Перечислите основные свойства функции синус.
6. Найдите наименьший положительный период функции:
a) /(x ) = s in ( 3 x + y - ) ; б) f (х) = tg 2( * ~ у-)-
7. Вычислите: a) tg -/2+ tg (—д/2); б) t g ^ - c t g ^ .
Перечислите основные свойства функции тангенс.
/з
8. Найдите arccos (— 1); arccos^-.
Сформулируйте определение арккосинуса числа. При каких а
определен arccos а? В каких пределах может лежать arccos а?
9. Решите уравнение: a) tg ^ 2 x — ^ = 1;б) 2 c o s(-|—f-l) = l.
Напишите формулу для решения уравнения sinx = a.
10. Решите неравенство: а) t g 2 x > l ; б) sin — 1.
11. Решите систему
j cos (* + (/)=0,5,
1 sin (х —у)= 1.
Вариант 2
1
1. Изобразите схематически график функции f (х)--
х (х—1) '
Что называют графиком функции?
2. Докажите, что для возрастающей на промежутке I функ
ции / уравнение f(x )= a для любого а имеет не более одного
корня на /. Верно ли аналогичное утверждение для убывающей
функции /?
3. Докажите, что функция f является нечетной:
а) / ( x ) = s i r i б) f (х)= х2tg х; в) / (х) = х7— 5х3.
Какие функции называют четными? нечетными?
4. Изобразите эскиз графика какой-либо функции g, обла
дающей следующими свойствами: 1) g возрастает на проме
жутках (— оо; 1] и [5; оо); 2) g убывает на промежутке [1; 5];
3) х = 1 — точка максимума функции, х= Ъ — точка минимума
функции, при этом g (l) = 4, g (5)—2.
Может ли функция g с указанными свойствами быть четной
или нечетной? Почему?
5. Укажите точки максимума и минимума функции cos ^ 2 х + - ^ .
102](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-104-320.jpg)

![6. Вычислите приближенно л/л/^7-
7. Найдите промежутки возрастания и убывания функции
f (х)= х — 2~фс.
8. Найдите максимумы и минимумы функции
9. Исследуйте функцию f (х)— х3— Зх — 2 и постройте ее
график.
10. Найдите наибольшее и наименьшее значения функции
f( x ) = x - |- i -
на отрезке [1; 3].
11. Запишите дифференциальное уравнение гармонического
колебания у = 2 cos (д/Зх— 1).
Вариант 2
1. Решите неравенство методом интервалов:
а) 3 , - 7 , ’ « 0 ; б) Д £ + 3)> 0 -
2. Напишите уравнение касательной к графику функции
у = 2х2— 1 в точке с абсциссой *о= 3.
3. Найдите производную функции у = 2,5л:2—х5; у = tg 2дс—
—2 c tg -|-. Каков геометрический смысл производной в точ
ке *0?
4. Маховик вращается вокруг оси, поворачиваясь за t секунд
на угол со (t)= 2t4— t (рад). Определите его угловую скорость
в момент времени: a) t; б) 2. В какой момент времени угловая
скорость маховика равна нулю?
5. Известно, что / . Найдите /' (х); f ' (2). Сформу
лируйте теорему о производной частного.
6. Найдите производную функции f (х) = (2х3— I)100.
Запишите формулу для вычисления производной сложной
функции.
7. Найдите промежутки возрастания и убывания функции
у = х3+ х.
8. Найдите максимумы и минимумы функции g (х)—л/х— х.
104](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-106-320.jpg)




![1. Решите уравнение:
a} sin jc= -—1; б) 2 cos2х —cos х — 1= 0 ; в) sin2л:+
+ д/3 sin х cos х = 0.
2. Решите неравенство sin х ^ —0,5.
3. Решите систему уравнений
[ х + у = п,
I sin x + sin у = —-]2.
4. Н е о б я з а т е л ь н о е з а д а н и е . Решите неравенство
|2 sin х — 11<11.
Вариант 2
1. Решите уравнение:
a) c o s x = — 1; б) 2 sin2jc—sin л:— 1= 0; в) cos2* —
— /3 sin х cos * = 0.
2. Решите неравенство cos xsgC—0,5.
3. Решите систему уравнений
( х --у = л ,
1 cos х —cos р = У2.
4. Н е о б я з а т е л ь н о е з а д а н и е . Решите неравенство
|2 cos х -f- 11^ 1.
Вариант 3
1. Решите уравнение:
a) sin * = 0,5д/2; б) 2 sin2x = cos х + 1; в) sin2x —2 sin x X
Xcos x = 3 cos2x.
2. Решите неравенство t g x ^ — 1.
3. Решите систему уравнений
Г х + у = ^ ~ ,
^ sin x + sin у = — Д.
4. Н е о б я з а т е л ь н о е з а д а н и е . Решите неравенство
2 sin2x + sin х — I <i0.
К о н т р о л ь н а я р а б о т а № 3
Вариант 1
Вариант 4
1. Решите уравнение:
а) созх = 0,5д/2; б) 2 cos2х — 1= siri х; в) sin2x +
+ sin х cos х = 2 cos2х.
109](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-111-320.jpg)

![1. Решите уравнение:
a) s in x = — 1; б) 2 cos2х —cos х — 1= 0 ; в) sin2x +
+ -/3 sin х cos х = 0.
2. Решите неравенство sin х ^ —0,5.
3. Решите систему уравнений
( х + у = л,
I sin x + sin у = —-]2.
4. Н е о б я з а т е л ь н о е з а д а н и е . Решите неравенство
|2 sin х — 11^ 1.
Вариант 2
1. Решите уравнение:
a) c o s x = — 1; б) 2 sin2х — sin х — 1= 0 ; в) cos2x —
— [3 sin х cos х = 0.
2. Решите неравенство cos 0,5.
3. Решите систему уравнений
/ х + г/= л,
cos х —cos г/= -у2.
4. Н е о б я з а т е л ь н о е з а д а н и е . Решите неравенство
|2 cos х + 11^ 1.
Вариант 3
1. Решите уравнение:
a) sinx = 0,5y 2; б) 2 sin2x = cos х + 1; в) sin2x —2 sin хХ
Xcos х = 3 cos2х.
2. Решите неравенство t g x ^ — 1.
3. Решите систему уравнений
( x + y = jr >
| sin x + sin у = — л[2.
4. Н е о б я з а т е л ь н о е з а д а н и е . Решите неравенство
2 sin2x + sin х — 1 ^ 0 .
К о н т р о л ь н а я р а б о т а № 3
Вариант 1
Вариант 4
1. Решите уравнение:
a) cosx = 0,5V 2; б) 2 cos2 х — 1= s ir i х; в) sin2 x +
+ sin х cos х = 2 cos2 х.
109](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-113-320.jpg)



![4. Напишите уравнение касательной к графику функции
f(x) — x2--2x в точке его с абсциссой х о = —2. Выполните ри
сунок.
5. Н е о б я з а т е л ь н о е з а д а н и е . Начертите схемати
чески график функции f (х), которая определена на проме
жутке (—5; 4], непрерывна в точке х = 2, но не дифференциру
ема в этой точке. Известно, что х = — 1 — точка максимума и
/ (— 1)=3.
К о н т р о л ь н а я р а б о т а № 6
Вариант 1
1. Исследуйте функцию / (х) = х3— Зх2+ 4 и постройте ее гра
фик.
2. Число 12 представьте в виде суммы двух неотрицатель
ных слагаемых так, чтобы произведение квадрата одного из них
на удвоенное другое слагаемое было наибольшим.
3. Докажите, что функция у (t)=7 cos 8^ является решением
дифференциального уравнения у " = —64 у.
4. Н е о б я з а т е л ь н о е з а д а н и е . Докажите, что функ
ция ф (х)= —4,3 х —cos2лг+ sin2х убывает на множестве действи
тельных чисел.
Вариант 2
1. Исследуйте функцию f (х)— —+ + 3х2—4 и постройте ее
график.
2. Число 9 представьте в виде суммы двух неотрицатель
ных слагаемых так, чтобы произведение квадрата одного из них
на утроенное другое слагаемое было наибольшим.
3. Напишите дифференциальное уравнение гармонического ко
лебания х = 3 cos (2 /+ 0,3).
4. Н е о б я з а т е л ь н о е з а д а н и е . Докажите, что функ
ция /(*) —2 sin л:-sin (0,5л+ х) + 3,2х возрастает на множестве
действительных чисел.
Вариант 3
1. Исследуйте функцию / (х)=-^—х3— 4х — 3 и постройте ее гра
фик.
2. Число 8 представьте в виде суммы двух неотрицательных
слагаемых так, чтобы произведение куба одного из них на дру
гое слагаемое было наибольшим.
3. Напишите дифференциальное уравнение гармонического ко
лебания x(t) = 3 cos 2t.
5 Заказ 68 113](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-117-320.jpg)





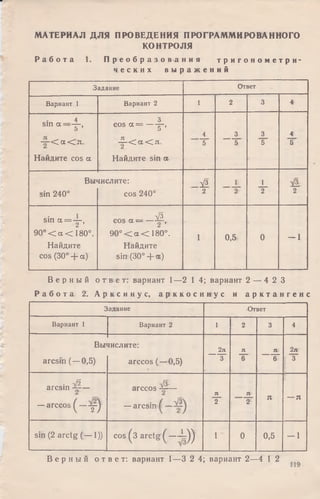
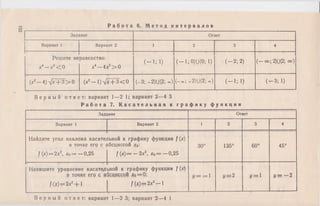
![Р а б о т а 3. О с н о в н ы е с в о й с т в а ф у н к ц и й
Задание Ответ (л£2)
Вариант 1 Вариант 2 1 2 3 4
Найдите облас
функ
и —_V L
у х2— 4
гь определения
ции:
У==Э—х2
x^>-Q, х ф 2 х ^ О , х ф ± 2 х < 0 , х ф —3 х ^ О , х ф ± 3
ц - х~ s m x — 1
у — x+lр COSX+1
х ф л - - 2 лп / ^ 1
Х ф — фпп. хф-^---2лп х ф л - - л п
Найдите промежутки
убывания функции
t/= 2x2—4 х + 1
Найдите промежутки
возрастания функции
у = 0,5х2+ х + 1
’(— оо; — 1] [— 1; оо) [1 ; о о ) ( — о о ; 1]
В е р н ы й о т в е т: вариант 1—1 3 4 ; вариант 2—3 1 2
Р а б о т а 4. Р е ш е н и е п р о с т е й ш и х т р и г о н о м е т р и ч е с к и х у р а в н е н и й
Задание Ответ {n^Z)
Вариант 1 Вариант 2 1 2 3 4
Решите у
sin х - ~ -
равнение
V2
sin X— — — -J-+ 2лт
( - 1 Г х + лга
(_!)«+*
Л 1
+ я п](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-124-320.jpg)
![ОТВЕТЫ И УКАЗАНИЯ
С а м о с т о я т е л ь н ы е р а б о т ы
Вариант 1
С —1.1. - j - и 2. 135° и 50°. 3. а) 0,8552; б) 1,3285. 4. а) 49°16',; б) 70°52'.
С—2. 2. а) Плюс; минус. 3. 0,5. С—3. 1. а) 0,5; б) — - . 2. — 1,— С—4. 1. —
,/3 sin а 2
527 336
2- — 625= 527' 3‘ 3 sin 2а. С - 5 . 1. a) ( - о о ; — 2)U( —2; 2)U(2; оо); б) ( - о о ; -0 ,5 ]U
U[0,5; оо). 2. I и х2 (при х ^ 0 ) . С—7. 1. Убывает на ( — оо;0,25], возрастает на
[0,25; оо). 2. Пусть х? > х и тогда х! >•■*?; складывая эти два неравенства,
получим ;t2+ *2> X i+X i, т. е. / (х2) > / (xi). С—8. 1. а) — cos 3°; б) — sin 79° =
Зл л 2л
= — cos 11°; в) ctg — = t g — . 2. 0. 3. а) Зл; б) -у “, в) Зл. С—9. 2. В озраста
ет на промежутках [— 2л + 8л k; 2л 8лй], k £ Z, убывает на промежутках [2л + 8л&;
6я + 8л£], k ^ Z . 3. [0,5; 1,5]. С—110. 1. /(х )> > 0 на интервалах ^ + БлА;
, fcg-Z, j(<x}c0 :на интервалах 1( 4 р + 6 л & ; -4^—)-&л£^ , k £ Z . 2. Мно-
я , лк „ 2л£ , „
жество всех действительных чисел, кромечисел вида—— Ь-гр-. 3. х = ——, « g z ,—
4 Z о
jt “I- 2 n k
точки максимума; х = -----=---------•, k ^ Z ,— точки минимума. С— 11. 2.(— оо;3].
О
_ _■» ( зт , nk Л Z l k 1 _ _ . _
3. Возрастает на промежутках ( ----- 8~ Т " ’ "*8— ^ — а '
— гг: б) 5 ? -2 . 3. а) — 1,1198; б) 1,3908; в) 0,3082. С— 13. а) ± ^ + 2 л / г ,
о о 4 о
kez; б) --11+ДД., в)- | ^ + л / г , AgZ. С— 14.а ) . [ - ^ + 2лй;
Д — |-2зтЛJ, fe£Z; 6) - £ - + ? ) • k e z - с ” 15- а) ( - 1)4- ^ - + лА'
б) — с- 17- ( х +лй; "I— пй) ’ /г£2‘ С~ 18- а)
g не определена в точке — 1; б) да (в обоих случаях); в) предел / в точке
— 1 не существует; lim g ( x ) = l . С— 19. 1. а) 10; б) 9. 2. а)5; б) 1,4.
Х -+ - — I
С—20. I. — 2Ах; — 0,4. 2. 2х0— 1+'А х; — 0,9; — 0,999; — 0,99999; предел равен
— 1. С— 21. а) — 7; б) — Дт. С—22. 1. а) 5х4— Х- б) -у . 2. — 9; — 297;
3 — 12х2; 3 — 12 (х + 2)2. С—23. а) 1,5; (1,5; оо); { - t o - 1,5); б) 0 , (— оо; — 2,5)1)
и( — 2,5; оо); 0 . С -2 4 . 1. а) ( - оо ; — I ) ( j ( - у ; у ) и ( у ; °о ) ;
123](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-127-320.jpg)
![Рис. 12
Рис. 11
б) ( — 1.5; 1,5). 2. и - y J — T - 3. а)
л/х — 1 ’ х ~ 1л/г
а) 2 cos 2х + 3 sin Зх; б)
300 (Зл — 4)"; б) I. С—25.
cos
1
; в) sin 2jc. С—26. 1. ( — о о ;0).
в 1 п *
(0; 2) и (2; оо). 2. а) ( - о о ; -2 )U (2 ; оо); б) [ - 4 ; — |-)и [2 ;6 ]; в) ( - 4 ; - 2 ) U
U(13; оо). С—27. 1. 27. 2. у = — Зх + 9,5. С—28. 1. 1,0004. 2. 1,035. С—29.
1. — 8; — 24. 2. 180 м. С—30. 1. Возрастает на промежутках ( — оо; — 3) и
(3; оо); убывает на промежутках ( —3; 0) и (0; 3). 2. х = — 5 — точка максимума;
х = 1 — точка минимума. С—31. Убывает на промежутках о о ; — и
Г1 Г 1 11 1H j-; оо 1 , возрастает на промежутке — — ; — ; х = — - — точка минимума;
х — -i точка максимума. С— 32. 1. График изображен на рисунке 11. 2.
а) [— 1; 18]; б) о о ; С—33. График изображен на рисун
ке 12. С—34. 1. m a x J = / ( — 1 ) = — 7-^-; min f = f ( 2 ) = — 32. 2. 5 + 5. С—35.
[ - 1 : 2 1
I. Д а. 2. у " = - у . С -3 6 . 1. 3. 3. VT5- С -3 8 . 1. а) у ; б) ^ . 2 . а) -£ +
+ 2nk, kez- б) - ± + 2nk, (-1)4-^+ лА, kez. 3. а) (у+ л*;у+"*].
*62; б) (л*; -^+ л /г), kez. С—39. 1. а) [—1;2,5]; б) (—о о ; — 2 —У3)и
U ( - 2 + V3; оо). 2. а) [ - 4 ; - 2 ] и х = 3; б) ( - 5 ; - 4 ) U ( - 3 ; 3)U(4; 5). С -4 0 ,
а) 12х5+ - ^ ; б) c tg x — ; в) ----- ?— ; г) — 2х sin х2; д) 4 -—
- fx ' ■7 2 X
7 cos —
С—41. 1. 0. 2. а) 1,00021; б) 0,15708. С—42. 1. Возрастает на (— оо; оо), экстре
мумов нет. 2. min f = f (1 ,5 )= 12; max f = f (0,5)— 20. 3. 180 H.
[0,5; 41 [0,5; 4)
124](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-128-320.jpg)
![Вариант 2
С— 1. 1. и 2. 150° и 85°. 3. а) 0,5411; б) 1,5077. 4. а) 30°56'; б) 82°5'
1Z 1о
С—2. 2. а) Минус; б) плюс. 3. — С—3. 1. а) 0,5; б) - Д 2. — . С—4.
Э COS GC
К 0 ’5- 2- S и ~ Ш 3- 2- С- 5- *• а) ( - ~ ; 0)и(о;4) и ( 4;оо);
4-1 , воз-
8 J
я
2. 0.
5
я k
~~2 ]' 8 +
растает на ["g"’ 00) - ^ *• а ) — tg 41°; б) — cos 43°; в) - s i n -
. 4л л . _ _ Л Л _ Г л , як л ,
3. а) — ; б) — ; в) 6л. С—9. 2. Возрастает на промежутках — —~—— +
о 5 L о 2 о
. nk~] . _ V я , як Ъя , я k~] п г ,
Т г убывает на промежутках I "g"Н—2"J »k ^ z - 3* [— 1; 3].
С— 10. 1. / ( * ) > О на промежутках ^ ; 1 Т + 4 г ) ’ k ^ Z ' на
( f2nk л 2я&
Т " ' Т + ~3~)
промежутках I —|— — ; — — — ), &£Z. 2. М ножество всех действительных
чисел, кроме чисел вида л + 2 яk, где fe£Z. 3. х — 10я£, k £ Z ,— точки макси
мума; х = 5л+ Ю л& , k £ Z ,— точки минимума. С— 11. 2. [3; оо). 3. Возрастает
л Зл
на промежутках (— я + 2яА; я + 2л&), k £ Z . С— 12. 1. а) — — ; б) я. 2. — — .
3. а) 0,9273; б) 1,8473; в) 1,2626. С— 13. а) - у + я £ , fegZ; б) у , * 6 Z,
в) - ^ - + ( - 1 ) ‘ -|- + лй, ££Z . С— 14. а) ^ + 2 я * ;^ ? -+ 2 я й ), ft£Z; б) ( - я +
+ 2лй; — |- + 2 я й ] , £(EZ. С - 1 5 , а) ± ^ + 2лk, AgZ; б) — 2 . + ^ , fegz.
С— 17. 0 2 + 2лй; 2 л й ); (2 л £ ; - ^ + 2л/г), 6 gZ. С— 18. а) / ( 1) = 1; g ( 1 )= 2 ;
б) предел / существует, предела g не существует; в) lim g (x ) = 2, предела f
Х -* ~ 1
в точке 1 не существует. С— 19. 1. а) — 16; б) 40. 2. а) 0; б) 3. С—20. 1. — ЗДх;
— 0,9. 2. 2х0+ 1 + Д х ; 1,1; 1,001; 1,00001; предел равен 1. С—21. а) — 6; б)
2 8х *
С—22. а) 14х6+ — ; б) — г а . 2. 20; 64; 4х + 3х2; 4 (* — 3) + 3 ( х - 3 ) 2.
-у* (■*
С—23. а) — 1,5; (— 1,5; оо); (— оо; — 1,5); б) 0 ; ( — оо ; — 2) (J( — 2; оо)- 0 .
С -2 4 . 1. а) ( - о о ; - 0 , 2 5 )U (-0 ,25; 0,25)11(0,25; оо); б) Г— ; -^-1. 2. Х 2 ± 1
/-------- L 3 3 J л/х + 2-[х--2
. 3. а) 320 (2х — З)159; б) - . С -2 5 , а) - 2 sin 2 х - 3 cos Зх;
с+2 Yi^ 3 ?
б) ~ 7 “ в) - s i n 2 x . С—26. 1. (— оо; — 2), ( — 2; 0) и (0; оо).
-л / х + 1
И Vjc+ 2
2. а) (— 3; 3); б) ( — со ; —3]U( — 0,5; 1]U[5; оо); в) (— 5; — 2)U(11; оо). С—27.
1. 27. 2. i/= 6x + 11. С—28. 1. 0,999992. 2. 0,999988. С—29. 1. 3; - 1 8 . 2. 80 м.
С—30. 1. Возрастает на (— оо; — 2] и на [2; оо), убывает на [— 2; 0) и на (0; 2].
2. х — — 1 — точка максимума; х = 5 — точка минимума. С—31. Убывает на
( — о о ; — 4] и на [4; оо), возрастает на [— 4; 4]; х — — 4 — точка минимума;
х — 4 — точка максимума. С—32. 2. а) ( — оо; — 16]U[1; «=); б) jc = — 1,5. С—33.
Убывает на промежутках (— оо;0,5) и (0,5; оо); экстремумов нет. С—34.
125](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-129-320.jpg)
![1. m ax f — f (— 2) = 48; min f = / ( 1 ) = — 6. 2. 12 + 6. C—35. J. Нет. 2. y” = - y .
[-2; II [—2; I]
C—36. 1. 3. 2. 0,25 tg 4a. 3. C—38. 1. a) у ; 6 ) y . 2. а) у + 2лА, A+Z;
6) - g - . k £ Z . 3. a) |д £ + л*; + > * £ 2 ; б) + k £ Z . C—39.
1. a) [ - 2; 5]; 6 ) ( - oo; 3 - V8)U(3+ 7 » ; °°)- 2. a) [1; 4] и x = - 2; 6) ( - o o ; — 4]U
U ( - 3 ; -2 )U (2 ; 3)U[4; о о ).-C -4 0 . a) 7x6-----% ; 6 ) tg jM ^ - 1 в) - ■ '
C° S X ' 3 s in 2 4 '
•J
8 4
r) 2XCOSX2; Д ) y —y . C—41. 1. 1. 2. a) 0,99999998; 6 ) 0,031416. C—42.
1. Возрастает на ( — оо; — 1] и на [1; оо), убывает на [— 1; 1]; х — — 1 — точка
максимума; х = 1 — точка минимума. 2. max f = f ( l ) = f (4)= 5; min f — f (2) = 4.
3. 144 Н. [1;*! ,fl;41
Вариант 3
С - 1 . 1. 1,1170; 2,7925. 2. 108°; 315°. 3. . С - 2 . 1. — 4-1 4 - - С - 3 .
2 2 5 4
1. - - L - . 2. 2. С - 4 . 1. а) _ § ; б) - Ц ± ± ; в) - ± . С - 5 . 1. а) 0; - 2
1; 4. 2. [0; V ^ 5 ) U ( ^ 5 , _<х>). С—6. а) Четная; б) нечетная. С—7. 0 ^ х < 4
С - 8. 1. а) — 1 ; б) Щ -, в) -л /3 . 2. tg 2а. С - 9 . а) у ; у ; 2 - 1 я; б) у
о 1 ч Л ^ ^ 5 л о 1 ^ i Г »» ч Л Я , 2 „ 1
2 у л ; в) у < * < у ; 2 у я < * < 2 у л . С -Г 0 . a) - у ; у ; 1 у л ; 2 у л
б) 0; 2л;в) — y C x c - i , 1 я < л : < 2 у л. С -1 1 , а) - у
ч Зл л я "Я , 1 — . л .
б) — л < х < — —; —— < х < — ; у < К 1— л. С— 12. а) -
в) г) д/З. С— 13. а) - у + 2ля, h 6 Z; б) 2л7е, A+Z; в) - у + у " ’ " eZ
г) ( — l)" д ) 2лн, — ^- + 2лл, n£ Z . С— 14. а) у + 2 я л < л :<
Зл л 2л л , л ,
< — 4- 2ля, б ) у 4- я л < ; л : < ~ 4-я /1., в) — — 4- л п < х < — + пп,
л л 2л
n £ Z . С— 15. а) гЬ-тг-4-ял,ti£Z б) (-— )п — ~~лп, n ^ Z в) ± - т 4 - 2 л я , n£ Z .
о Ъ о
С— 16. а) —-?";ь 4 г ,!’ n €Z; б) — ^- + яя, arctg 5 + лл, ng'Z. С— 17. а) +
8 2 4 12
+ 2лл, у + 2 я л , n£Z ; б) ля, — ^- + ля, n £ Z . С— 18. а)Возрастаетна [0; 1),
убывает на ( — оо;0] и [1; оо); .-б) lim /( * ) = 1 ; в) не существует. С — 19.
x-^—I
1. (1,95; 2,05). 2.а) 5; б) - 1 2 ; в) 10. С— 20. 1. 3. 2. 2,6. С—21. 1. — 8. 2. —у .
С—22. I. 0; - 1 . 2. 8 х; 2. 3. а) •2 2; б) (— оо; 1>Н(1; оо). С—23. 1. 7 [? , 189.
(I ■X)
2. [ — 3 ; 4 ] - 3‘ а С —24. 1. [— 4; 2)U(2; 4]. 2. — 60. С—25. 1. а) —6sin 2х
—Зл/5; б > !f - ; 12. 2. л + 2 л й . ± ^ - + 2nk, A+Z. С—26. а) (1; 3); б) ( - 2 ; - 1)U
COS ОХ о
U(l; оо). С—27. a) </=4* + 8; в) 8. С—28. а) 6,933; б) 0,8573; в) 0,7314.
126
я
1— л
т 4
я л
У ’ б) У
+ —
^ 2 л, n g Z](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-130-320.jpg)
![С—29. 202 см2/с. G—30. а). Возрастает на [— 1,5; оо); убывает на ( — оо; — 1,5];
б) возрастает на Л; в) возрастает на ( — о о ;0 ] и [2; оо), убывает на [0; 2].
С—31. а) Х— — 2 и х = 2 — точки минимума, /(-— 2 )= /(2 )Г = — 16; х — 0 — точка
максимума, f ( 0) —0; б) х = — 4 — точка максимума, / ( —4):= —2; х = 4 — точка
минимума, f(4 )= 2 . С—32. х — — /2 и х = ф 2 — точки максимума, / ( — /2) =
— — 4; x = Q — точка минимума, / ( 0) = 0. С—33. х = — 2,—- точка макси-
4 4
мума, / ( —2) = 4 — ; х — 2 — точка минимума, / ( 2 ) = — 4— ; х = 0 — точка
15 ч 15
перегиба, / ( 0) = 0. С—34. т а х f ( x )= f = min / (х) = / ( - ^ Л = 0 .
, , ИК HI ,С -3 5 . 1. 12 c o s ( 2* + y ) , - 2 4 з г п ( 2 * + у ) , бфЗ, — 1 2 ^ С -3 6 . 2. + Щ -
С—38. 1. — ^ -+ я п , n£Z: 2. — ^ + я т г ^ х ^ —у п + я л , n ^ Z . 3. л + 2лл, rr£Z.
о 1*2 12
С—39. а) (— оо; — 4]U(0; 2)U[4; оо); б) ( — оо; — 2]U[2; 5]. С—40. 1. а) — Y '
cos Зх *
cos х 2х sin х
б) — ; в) sin 2х; г) —9.sin Зх (cos Зх + 6)2. 2. — 8. С—41. 1. Точка
2-ух
с координатами (1;0). 2. у = х — 1. С—42. 1. Слагаемые 4 и 4. 2. х = 0 — точка
максимума, f ( 0) = 0; х — 1 — точка минимума, /(L )= — 1.
Вариант 4
С— 1. 1. 0,9774; 2,9671. 2. 150°, 390°; 3. С -2 - 1- X , - ^ г .
б 2 20 Z4
' О , г л Т 4 + 3 V 3 . 1
cos а ' 25 ’ 10 ’ 7
2. (— о о ; — — /2i 0]. С—6. а) Нечетная; б) четная. С—7. 0^Сх<Г2.
С—8. 1. а) — у ; б). у 7 в), —л/ i 2. —e tg 2 a . С—9. а) у , у , 2 у я,
« 3 , , я З я , я Зя „ 1 „ 3 „ , я я
2 т я; б) у ; в) т < Ж у ,. г у Ж ж г у я . С -1 0 , а) - у . у .
, 5 _ 1 , я я , 5 1 _ , 1
1— я, 2 -2-л ; б) я, Зя; в) — т < х < -~Г • и < Ж 2 - ^ - я . С— 11. а) — 1— я,
О О 0 0 0 0 4
л Зя , , , 1 я я я Зя ^ „
— Г - т • б) — 1— я < х < — — , — —< х < , ------ < х < я . С— 12.
4 4 4 2 4 2 4
а) — ; б) у ; в) —л/3; г) — i - . С— 13. а) я + 2ял, n £ Z ; б) у + 2ля, n g Z ;
в) —- у + у " , " € Z ; г) ± у + ^ , ngZ ; д) 2лл, у + 2лл, ng Z . С— 14. а) —у +
л 5л - л л
+ 2лл < * < - - } - 2лп, rt£Z; б) —- ^ - - л п С х < С — j --fro * , n£Z; в) — —-f л л <
< т < у + лл, H6 Z. С -1 5 , a) d r y + ЯЛ, n £ Z ; б) (— 1)*+' у + л£, fc£Z; в) ± у +
+ 2лл, n £ Z . С— 16. a) y + y n > n £Z; б) — ^ -+ я л ;. — arctg 3 + лл, n £ Z .
2л л
С— 17. а) — + 2ял, n fZ ; 6) ял, ——|-л я, n £ Z . С— 181 а) Возрастает на каждом
о 4
из промежутков- ( — оо; — 1) и [0; оо); убывает на промежутке- [т— f,.0];
29 1
б) lim / (лг)=0,5; в) не существует. С— 19. 1. 1— < х < 2 — . 2. а) 6; б) — 18;
х-» 5 0 30
1 fi
в) 2. С—20. 1. 2. 2. 1,4. С—21. 1. — 18. 2 .— . С—22; 1. 0; 1. 2. 8х; 4. 3. а) 7- 7- 775;
-фс (х ~ г 1Г
127](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-131-320.jpg)
. 3. 4. С—24.
1. (— оо; —7)U( — 7; — 5](J[5; оо). 2. — 24. С—25. 1. а) 10 cos 5*; 5; б) — - J j ^ ;
—6. 2. лп, ngZ. С—26. а) (—2; — 1); б) (— оо; — 1)(J(1; 3). С—27. а) у = —4л:—8;
в) 8. С—28. а) 6,085; б) —0,4699; в) 0,6018. С—29. 603 см2/с. С—30. а) Воз
растает на промежутке ( — оо; 2], убывает на [2; оо); б) возрастает на Л; в) воз
растает на каждом из промежутков (— оо;0] и [1; оо), убывает на [0; 1].
С—31. а) х = — 1 и х = 1 — точки минимума, / ( — 1)= /(1 )= — 1; х = 0 —
точка максимума, f(0)=l; б) х = —6 — точка максимума, (( —6 ) = —3;
х = 6 — точка минимума, / ( 6) = 3. С—32. х = —у/2 и х = д/2— точки минимума,
/ ( — [ 2 ) = f (-/2)= 0; х = 0 — точка максимума, /(0) = 4. С—33. х = — 1 — точка
минимума, / ( — 1)= — 1-— ; х — 1 — точка максимума, /(1 )= 1 — ; х = 0 — точка
О О
перегиба, / ( 0)= 0. С—34. max / (х) = / f-?-') = 1 4 -; min ( М = /(0) = 0.
И ] И ]
С—35. 8 c o s^ 4 x + -|- ); - 3 2 sin (4х + у ) ; 4; - 1 6 . С—36. 2. . С—38.
1. — g- + n п> n ^ Z - 2' + ’ n ^ Z ‘ 3' — т у + 2ля, n£Z . С—39.
а) [ - 3 ; 0)U[3; 5); б) [ - 5 ; -4]U [4; оо). С -4 0 . 1. а) - - ^ ; б) -*‘£ £ ± ^ 5 -21 ? ;
в) —sin 2х; г) 6 cos 2х (sin 2х —5)2. 2. 8. С—41. 1. Точка с координатами (1; 0).
2. у = —х + 3 . С—42. 1. Слагаемые 9 и 3. 2. х = —2 — точка максимума,
/ ( —2)= 4; х = 0 — точка минимума, /( 0) = 0.
Вариант 5
С— 1. 1. ~ и 2. 165° и 517°30'. 3. а) 1,3788; б) 0,6696. 4. а) 43°24';
5 У
б) 116°4Г. С—2. 2. а) Плюс; б) минус. 3 . С—3. 1. а )
б) ^ ; в) 2‘ - f sin22“- с- 4- *• 2- - W 3- - cos4“'
С—5. 1. а) (— оо; 1)U(1; 6)U(6; оо); б) (— оо; —2)11(2; оо). 2. - 1 5 ; х3+ Зх2+
+ 6х + 3. С—7. 1. Для любых х2> х , > 1 имеем: / (х2)—f(xl) = x2—Зх2—х3+
+ 3 x i= (x 2—Х|)(х2+ х,х2+ х1 —3 )> 0 , так как х2—х , > 0 и х2+ х,х2+ х ?> 3 .
2. Возрастает на ( — оо; 1], убывает на [1; 0). С—8. 1. а) —sin 34°43';
б) sin 0° = 0; в) t g 4 r - 2. —л/З. С—9. 2. х = ^ + ^ , AgZ, — точки макси-
7Т О ттЬ
мума, х = |— -— , k £ Z ,— точки минимума. 3. sin 100°, sin 150°, sin (—200°),
42 3
sin 10°, sin (— 100°). С— 10. 1. cos 70°, sin 40°, cos 40°, sin 70°. 3. Убывает
на промежутках - A n k ^ - + 4 n f tj , fcgZ, возрастает на промежутках
£ — ^ - + 4 n * j , k £ Z . С— 11. 2. Возрастает на промежутках
— - —р — ; “ + , ft£Z. 3. М ножество всех действительных чисел, кроме
8 2 8 2 /
чисел вида -т—Ь -тг» k £ Z . С— 12. 1. а) б) 0,1. 2.— . 3. а) 1,1130;
4 2 о 4
C j. 5л лА?
б) 2,4544; в) — 1,3258.С -1 3 , a) ± - ^ - + 2 n k , k £ Z ; б) — + 2л/г, k £ Z; в) — ,
, г, ^ . . ч ( л , 5л 2л& , , , г , Г л л/г л л/г
* € Z . С - 1 4 , а) ( т + — 1 ! - + — ) . ^€ Z ; б) [ - - + - у = T + t ) ’ ^
128](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-132-320.jpg)
. С—27. 1. у = х + 2. 2. у = —^ х + ^ - я + -^ -. С—28. 1. 5,9925.
32
2. 0,16. С—29. 1. 6Н. 2. 2 — м. С—30. 1. Возрастает на ( — оо; — 1] и на [2; оо),
4 5 ^
убывает на [— 1; 2]. 2. х = 1 — точка максимума. С—31. Убывает на (— оо;0]
и [3; 6]; возрастает на [0; 3] и на [6; оо); х = 0 и * = 6 — точки минимума; х = 3 —
точка максимума. С—32. 1. Возрастает на (— оо;2], убывает на [2; оо); х = 2 —
точка максимума. 2. а) ( — оо; оо); б) [— 0,5; 3,5]. С—33. Убывает на (— оо; — 1]
и на [0; 1], возрастает на [— 1; 0] и на [1; оо); * = ± 1 — точки минимума;
х = 0 — точка максимума. С—34. 1. min / = / ( — 2 )= — 55; max f = f (2) = 57.
[ - 2; 2] [ - 2; 2]
2. 4 + 2. С—35. 1. Д а. 2. х " = — 2х; А = 3; to = ->/2; ф = 2 я — 1. С—36. 1. 0.
„ , „ /к . v 2 — /2 _ „ , 2я „ л , л „ , л л
2. 4. 3. у/2— 1 и ' — - . С—38. 1. а) — ;б) — ; в) — — . 2. a) - g - ± —
+ я£, k£Z ; б) - j —(-лй, хо + л&, A+Z, хо = arctg 3 я; 1,249. 3. а) ^ — j —[
8 8
як
2 ’
k £ Z ; б) ^ + 2 л А ; - ^ + 2 л * ) , k £ Z . С—39. 1. а) [1; 3];
б) (— оо; 3)U(3; оо). 2. а) [1; 3); б) (1; 1,25)U(2; 3). С—40. а) 6х5- 1 2 х 3+ 6х2;
б) — ; в) 2 cos 2х; г) у — — г ; д) 34 (2х— I)16. С—41. 1. 1/ = х + 1 .
Л
1ЛМ8 1 2 )
-fx 3 cos'
( t - 0
2. a) 0,999; 6 ) 1,015. 3. 7; 8. С—42. 1. Возрастает на промежутке ( — оо; 1],
убывает на промежутке [1; о о ) ; х = 1 — точка максимума. 2. min / = / ( — 1)= 0,5;
m ax f = / ( 0 ) = l . 1- 1: 0,51
[- 1 :0 ,5 1
Вариант 6
С— 1. 1. -^ -и 2. 105° и 945°. 3. а) 0,9948; б) 1,5519. 4. а) 50°24'; б) 134°12'.
129](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-133-320.jpg)
![С—2. 2. а), б) Плюс. 3. -jL r; 4 “ - С —3- 1. a) 4 r i б) в) 1— . 2. 1.
УЙ) 3 2 . 2 -л/3
С - 4 . 1. ?-V t ± 3 g . 2. 3. 1. С - 5 . 1. а) ( - оо; 2)U(2; 3)U(3; оо);
б) (— 4; 4). 2. 4; 2л:3— блг' + бл:-!- 4. С—7. 1. Пусть 1^ jc2> jci ^ — 1. Тогда
f { x e b ~ x i ) ( x l - { - x 2xi + xi — 3 ) < 0 , так как x2— x > 0 , a xi + x2xi +
+ jc?< 3 (лг1^ 1, лс?<М, x 2x <C 1). 2. Возрастает на ( — oo;2], убывает на [2; оо).
С—8. 1. а) — sin 47°41у; б) cos 2°; в) c tg - J - . 2. У3- С—9. 2. x = ^ - - - n k ,
О ZU
fegZ,— точки максимума; х = —^ + л£, ftgZ ,— точки минимума. 3. sin (— 250°);
sin ( — 300°); sin 40°; sin 20°; sin ( — 150°). С— 10. 1. sin 15°; cos 70°; co s( — 20°);
cos 10°. 3. Убывает на промежутках —f-блЛ; —|-6n&J , fcgZ; возрастает на
промежутках £ — -i-jp -+ 6nfe; - ^ - + 6nftJ , fegZ. C— 11. Убывает на промежутках
^ ^ —(-2лб; Д ^ -+ 2 л /г ^ , k £ Z . 3. М ножество всех действительных чисел,
кроме чисел вида k £ Z . С— 12. 1. а) — б) — 0,3. 2. — 3. а) —0,8271;
о о о
б) 3,0641; в) 1,3068. С— 13. а) { - 1)*+‘ -j~ + n k , k £ Z; б) 2лА; — ^-+ 2 л Л ,
kez- в) у + ^ , * 6 Z. С -1 4 , а) ( - ^ —Ьл£; ^ + я * ) . * 6 2 ; б) ( — £ +
+ ^ ; 1 + + + Ч , * £ 2 . С -1 5 . а) -Т -+ Л *; х0+ лй, ft£Z, х0= arctg 3 « 1,249;
о «зо о / 4
б) - ■ ^ + Л Й , ft€2. С - 1 7 . ( ^ - + л А : + ^ ; _ . £ - + * * — у - ) , *£Z , n£Z .
С— 18. 1. а) 1; 2; б) 1; — 1. 2. 0,001. С— 19. 1. а) — 5; б) — 0,2. 2. а) 53;
Д у
б) — 2. С—20. 1. 0,5Длс; 0,1. 2. 3 —х0— g -; 3,95; 3,999; 3,999995; предел равен 4.
С -2 1 , a) б) 2х. С -2 2 . 1. а) 7*б+ 1 0 х 4— ; б) - £ ± g + l . 2. 1;
* 4 - ( - - • Ч М 4 - ~ М - т •
4 - ) ; б) 0 ; ( - 00; — 1)U( — 1; оо); 0 . С -2 4 . 1. а) [0; 4]; б) ( - 00; 1)U(2; 00).
/------
2. .1 + i L и V 1+ - - - 3. а) 191 (5х4- 4 х ) ( х 5- 2 х 2)190; б) "*■■■■ С -2 5 .
1 — 2 л/х 1 —2лс У 1 - х 2
2
а) 4 sin (3 —4х); б) -—а ; в) cosxcos(2x — 3) — 2 sin лсsin (2л: — 3) = cos(3x —
— 3)— sin л:sin (2л: — 3). C -2 6 . l . ( - o o ; — 1), (— 1; Г), (1; 3) и (3; оо). 2. а) ( - 00; 1)U
U(2; оо); б) ( - 3 ; — 1)U(— 1; 2); в) ( - 3 ; - |-)и [2 ; 6]. С - 2 7 . 1. у = х + ^ - ^ - .
2. г / = — 0,5х — 2. С—28. 1. 7,005. 2. 0,3. С—29. 1. 0. 2. 4,3375 м. С—30. 1. Воз
растает на (— оо; — 2] и на [1; оо), убывает на [— 2; 1]. 2. лс= — — точка минимума.
С—31. Возрастает на ( — 00; — 1] и на [0; 1], убывает на [— 1; 0) и на [1; оо).
С—32. 1. Возрастает на ( — 00; 1], убывает на [1; 00); х = 1 — точка максимума.
2. а) 0 ; б) (— оо; оо). С—33. В озрастает на ( — оо;0] и на [2; оо), убывает
на [0; 2]; лс= 0 — точка максимума; х = 2 — точка минимума. С—34. 1. m in^/ =
= f (0) = 3; m ax f = j { 1)= 24. 2. 6 + 2. С—35. 1. Нет. 2. х " = - 3 х ; Л = 4 ~ ;
130](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-134-320.jpg)
![и
ш = УЗ; ч = 2 . С—36. 1. —Ц . 2. — cos 8а. 3. 2 — л/3 и У2 + ^ • С—38. 1.
а) ; б) -g~: в) — 2. а) — у + ( — 1)*-^—-2nk, ££ Z ; б) -^ -+ л й ; х0+
+ л/г, fc£Z, хо = a rctg 0,32. 3. а) —(-2лА; л + 2лА ^, k £ Z ; б) ^
+ 2л*; ^ j - + 2 n k ) , fe£Z. С—39. I. a) (-o o ;2 )U (4 ; оо)-, б) 6. 2. а) ( - о о ; -2 ]U
U(3; оо) и х = 1 ; б) ( - о о ; - 2 ) U ( - 1 ,5 ; -1 )U (1 ; оо). С—40. а) 7х6- 1 0 х 4+ 3;
б) _ L d l^ . в) _ 5 s in 5 x ; г ) ------------------- г-;д) —6^ . С—41. 1. у =
2 V* 2 sin2 ( 4 _ + 5j W 7
= 7х— 2. 2. а) 1,001; б) 0,9982. 3. 23; 19. С—42. 1. Возрастает на промежутке
( — оо, 2], убывает на промежутке [2; оо); х = 2 — точка максимума. 2. min f =
[-2 ; 0,51
= / ( — t ) = — I; max f = f (0,5)=0,8.
I—2: O.Sj
Вариант 7
С— 1. t. 4 ^ и 4 т ^ - 2. 50° и 1740°. 3. a) 1,2462; б) 0,5111. 4. a) 2°6'; б) Г14*47'
oU 15
C—2. 2. а), б)Плюс. 3. — . C—3. 1. a) -y= ; 6) 0; в)— 1. 2. 1.
■■ ^ - # ■ з- й Н - ■> [ f = 2)
U(2; oo); 6 ) [2; 2,5). 2. a) — 1; 3; 0; — 1. С—7. 1. Убывает на ( — оо; 1) и на
(1,оо). У к а з а н и е . ^ 7 = 3 + — -. 2. х = 1 ,2 5 — точка максимума.
С—8.1. а) — cos41°43'; б) - c o s 20°; в) - t g Щ -= - c t g . 3. а) б) я.
О I (J Z
С—9. 2. sin 4; sin 3;sin 1; sin 2. 3.£ —у ^ -+ 2 л £ ; ^ - + 2 n * J , k £ Z . C— 10.
Л 2nk 71
2. — -— — , fegZ. 3. — + 2 л k, &£Z. С— 11. 1. М ножество всех действитель-
л nk / 2л
ныхчисел, кроме чисел вида ——|—— ,A£Z. 3.Возрастает на ( -------- -—-2nk;
Д.ТГ ТГ 7Я
— 4 -2 я Ы , k £ Z . С— 12. 1. а ) — — ; б) . 2. Первое меньше. 3. а) —0,3275;
б) 2,4966; в) 1.2729. С -1 3 , а) - ~ + п к , * € Z ; б) _ -£ - + ( - 1)“ ~ + nk, A£Z;
в) ^ + * 6 Z. С -1 4 , а)[ _ ^ + 4л*; _ ^ + 4я*] , k £ Z ; б) ( з - ^ +
+ 3лк-, З - ^ + З л ф k £ Z . С— 15. а) —у + 2лА>, k £ Z б) л*; - | - + л *. *£Z .
С— 17. ^ у + 2 л й ; 4 4 + 2 я л ^ ; + 2л£; у + 2 л л ^ , A£Z, n £ Z . С— 18. 1. а) — 0,5;
—0,5; б) 0,5; — 1,5. 2. 0,002. С— 19. 1. а) — 1 4 - ; б) 1 2. а) —6,5; б) 0.
3 * 8
С—20. 1. (2 х о -3 ) Дх + А х 2; а) -1 ,2 5 ; б) - 6. 2. ЗхК- 5 + Зх0Ах + Дх2. С -2 1 .
а) - 5 ; б) 2 х —4. С— 22. 1. а) 7х6- 15х4— б) 3* + 5 , 2. - 1 3 ; — - ;
хл[х 2 -у/х 13 ’
131](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-135-320.jpg)
![- , '4"ЕД ; - l4 . С -2 3 , а) 0; ± 0 .5 ; ( - 0 ,5 ; 0)U(0,5; оо); ( - о о ; -0 ,5 )U (0 ; 0,5);
(х + 5) х
б) 0 ; ( — оо; 2)U(2; оо);0 . С—24. 1. а) [3; 4)U(4; оо); б) [0; 41 2. sin3 x + 2 s i n x
и sin (x 3+ 2x). 3. а) 2020 (*3- * 4)(5*4- 4 х 5)100; б) ‘Л С -2 5 .
Ух —2х
2 / 2 3
а) — — sin ( -л -х — 1 I ; б) 3 cos Зх; в) —sin х cos 2х — 2 cos х sin 2 х гтг-.
3 3 / cos3 2х
С - 2 6 . 1. ( — оо; 0), (0; 1), (1; 6), (6; оо). 2. а) [ - 8; -2 )(J[9 ; оо); б) ( - 3 ; 4).
С—27. 1. У= 7 Г + - ^ ( х —у ) • 2- У= 2х — 4. С—28. 1. 4,01. 2. 2. С—29.
1. — 3 2 ^ ' 2‘ а ) "(Г ’ ^ с' ^ в о з р а с т а е т на ^ — оо; — y j и
на [1; оо), убывает на —у ; 1j . 2. х = ± У б — точки минимума. С—31. Убы
вает на (— оо; 1), возрастает на (1; оо), экстремумов нет. С—32. 1. Убывает на
( — оо;0,3], возрастает на [0,3; оо); х = 0 ,3 — точка минимума. 2. а) (— 2; — 0,5);
б) 6. С—33. Убывает на ( — оо; — 3] и на [5; оо), возрастает на [— 3; 5]; х = — 3 —
точка минимума; х = 5 — точка максимума. С—34. 1. min / = / ( — 4 )= — 130;
[ — 4; 2]
m ax f = f (2 )= 14. 2. 8 см; 2-/3 см. У к а з а н и е (рис. 13). Решим задачу в
более общем виде. Пусть в треугольник с основанием а и высотой Л вписан
прямоугольник наибольшей площади; найдем стороны прямоугольника и его
площадь: И з подобия треугольников А Р К и А С В имеем: (h —y):h = x'.a, откуда
x==a { h - y ) _ S = xy= zay ( ° - J } .' S ' и S '( y ) = 0 при y = j - . Д алее,
S (0) = S (Л)= 0, поэтому m ax S = S ^ y ^ = y . При этом x = 0 ,5 a , г/= 0,5/г. С—35.
1. у = А cos . 2. х" = — А = 2, о) = у , <Р= у • С—36. 1. — 1
2. — cos 4а. 3.
2 гг __ . . л л . Зл Зл&
у и У2. С—38. 1. а) л; б) — у ; в) - у . 2. а) — у - , A£Z;
б) ( - 1 ) * у + я £ ; (— 1)*+ 1хо+ л £ , ££Z , x0= arcsin 0,75яй0,8481. 3. а) ( —
у + у ) . &6 Z; б) ( ^ + л й ; ^ J + л / г ) , fe£Z. С - 3 9 . 1. а) ( _ о о ; ^ = ^ ) и
и № - ) = »»
з) [ — 5; у ) и х = 3; б) ( -
и(Чт;-т)и(1;оо>-
а) 8х7- 1 8 х 5+ 6х; б)
-4; - 3 ] . 2.
I)U
1 х
в) - у cos - у ;
С -4 0 .
Зх+ 6
2Vx+ 3’
2
Рис. 13
cos2(2x—у)
д) - 2 1 0 х ^ у - З х 2) 3’ • С - 4 1 . 1. у =
= — 2 х + 3 . 2. а) 1,00001; б) 1,015.
132](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-136-320.jpg)
![3. ; ~ ^ 2 ■ С —42. 1. Убывает на ( — оо; — 2] и на [0; 2], возрастает на
[—2; 0] и на [2; оо); х = ± 2 — точки максимума; х = 0 — точка максимума.
2. ш ах / = / (-—1) ==3; min /= = /( —2) = — 2.
1-2; 0] [—2; 0]
Вариант 8
4л 47л
С— 1. 1. и 2. 33°45' и 440°. 3. а) 0,4119; б) 1,4640. 4. а) 5°42';
б) 177°4Г. С—2. 2. а), б) Минус. 3 . -----; ----------- L . С—3. 1. а) ^ ; б) - 1 ;
уП) yio 2
■’ i - с - ' '■ J r i ' 2- 3- с- 5- '• ■' - 'W
астает наи ( — 1; 0°); б) ( - о о ; - 2 ) и [ у ; ° ° ) . 2. а) 1; 0; 0; 1. С—7. 1. Возр
( — оо; — 1) и на (— 1; оо). 2. лг= 1,5 — точка максимума. С—8. !. a) cos 33° 17';
б) tg 6 0 ° = y 3 ; в) cos — . 2. — /3. 3. а) 6л; б) л. С—9. 2. sin 1,5; sin 0,5;
sin 3; sin 4,5. 3. |Д + 2л£; ~ + 2 n * j , k £ Z . С— 10. 2. ^ + 6л*, k£ Z . 3. +
+4л& , k £ Z . С— 11. 1. М ножество всех действительных чисел, кроме чисел вида
^р + 3л£, k £ Z . 3. Возрастает на ^ k ^ 2" С— |2 - '• а )
б) 12° = - ^ . 2. arccos 1 < arctg 1. 3. а) 1,4279; б) 1,9538; в) — 1,3977. С— 13.
a) - y + nfe, А е г; б) Щ + 2л/г, £ 6 2 ; в) - у + ( - 1 )4 у + 2 я й , AgZ. С -1 4 .
. / я , л& я , л £ , _ , , Г 7я , 11я , ,1 , „
а) ( (Г Т : 12 " 3 ) ’ 6 ; б) |_24 ~24 ^ С- 15-
а) я + 2лА, £ £ Z ; б) лА; - 4 + я *. С— 17. + I -т- + 2 я я —
3 4 2 4 2 /
&6 Z, n ^ Z . С— 18. 1. а) 0; не определена; б) 1; 1. 2. 0,006. С— 19. 1. а) — 3 -}г ;
о
9
б) не существует. 2. а) — 163; б) —— . С—20. 1. 2хоАх + 2Ах + Ах2; а) —5;
б) - 1 у - 2. З х З -И + ЗхоДх + Дх2. С - 2 1 , а) - 7 ; б) 2х + 3. С -2 2 .
,. . ) 8, ' - 1 2 ^ 2 . 5 ^ « А Ь й . 2. ± ; J g ; ' ;
С -2 3 . . ) 0; ± 1 ; о ) и ( | ; « ) ; ( - - ± ) и (о ; ± ) ; б) - 3 и
7 ; ( — оо; — 3)U(7; оо); ( - 3 ; 2)U(2;7). С - 2 4 . 1. а) [ - 2 ; 14)U(14; оо); б) [0; 25).
2. (cos х + I)4— 2 cos х — 2 и cos (х4— 2 х ) + 1. 3. а) 3633 (х2—х6) (7х3— Зх7)'72;
Зх? з 3 /3 v I
б) — ------ . С— 25. а) — cos ( — + I ) ; б) — 2 sin 2х; в) --- *— (-cos х sin 2х +
2 У х ^ У к 7 V 7 т У
+ 2 sin х cos 2х. С—26. 1. ( — оо;0), (0; 2)- (2; 3); (3; оо). 2. а) (— оо; —2)U(0; t]U
U[3; 5]; б) ( — 2; 3). С—27. 1. у = “ у ( х - у ~ 2 ^ • 2. у = - 2 х + 2. С—28.
2 8 о
1- 9-^-—. 2. 0,0014. С—29. 1. —зс=Н. 2. 1,04 — ; 25с. С—30. 1. Возрастает на
300 27 с
( — со; оо). 2. х = ± У б — точки минимума. С—31. Возрастает на ( — оо ; 3),
убывает на (3; оо), экстремумов нет. С —32. 1. Убывает на возрастает
133](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-137-320.jpg)
![на оо^ ; точкаминимума. 2. а) [—3. 11]; б) ( — оо; — 4)U( —4; оо).
С—р33. Убывает на ( — оо; — 2] и на [4; оо), возрастает на [— 2; 4]; х — — 2 — точка
минимума; х = 4 — точка максимума. С— 34. 1. m in / = / (1 )= 5 ; m ax f —J (4)= 62.
(I; 4] [1; 4]
2. 12 см, 3V3 см. У к а з а н и е. См. указание к вар. 7. С—35. 1. у = 4 cos ^2х + - ^ .
2. х " = - 9 х . С—36. 1. 2 + ^VlO 2 _ J _ cos4(X. з. - д / l ; J j L . С—38. 1.
9 4 V JO V 3
. 5л л . л л . зх , л к л . л к . , _ л; , _ .. , _ _
а) -6 ; б) ~ Т : в) Т - 2- а) -6-+ y ; Т 8 + Т ’ ckeZ; б) ±-з+2п*’ *ег-
3. а) ^— я + 2я/г; - y + 2 n f c j , * 6Z ; б) ^ + п* )> С—39. 1.
„ ( ± - Е , 5 ± з И ) , о , г. { - о о ; - 1 ) и [ 8 ; ~ > ; 6, ( - » 4 ) и
u f - ^ ; 4-^U (2; оо). С -4 0 , а) 3 — 21хг + 2хг+ ’9 ^ б) 3^,+ 10 ; в) - 0 ,3 sin 0,Зх;
*о * / 2-yjc тЬ 5
г) 3------ -- ; д) 80х (5х2— I)7. С—41. 1. у = — Зх— 3. 2. а) 0,999999; б) 0,9895.
sin2 ( ^ — Зх)
2 4
3. — ; —ТоЕ- С—42. 1. Возрастает на (— оо; — 1] и на (0; 1], убывает на [— L; 0]
ZO 1ZJ
и на [1; оо); х = ± 1— тонки максимума; х = 0 — точка минимума. .2. т а х ^ / =
= / ( — 2) = 22; min / = / ( 0) = 2.
1— 2 ; в ]
Вариант 9
л 9зс 9л
с — 1. 1. ~ . 2. а) - 7 2 ° ; б) — 4248°. 3. 22°30'; 52°30'; 127°30'; 157°30';
0,3927. 4. 35°25'; 21°53'. С—2. 2. а) Минус; б) плюс. 3. 2 ctg а ; — 1. С—3. 1. 1.
2 .1 . С—4. 1 -4 - ..2. - 2 4 - . 3. cos 8а. С— 5. 1. a ),[— 1; 0)11(0; 3)У(3; оо); б) [0; 20,25].
О 4
2. а) 8; 5; 3; х2. С —6. 1. а ), б) Д а. С—7. 1. а) Убывает на ^ — оо; , возрастает
на ° ° ) 1 0) возрастает на ( — оо; — 1] и на [1; оо), убывает на [— 1; 0) и на
(0; 1]. 2. а), в), д) Возрастает; г) убывает. С—8. 1. См. рис. 14. 2. а) я; б) я-/2.
3. а) Р е ш е н и е. Пусть Т > 0 — период функции f (x) = sin х2. Тогда f ( T ) = f (0) =
= 0 , поэтому 7 имеет вид -1лпо, где (так как sin х2= 0 при х2= л я , т. е.
х — +л[лпо)- Но тогда на интервале (0; 7) функция имеет (по—Т) нулей (в част
ности, при по— 1 ни одного нуля), а на интервале (Г; 27) имеет 4по — по— 1— Зпо— 1
нулей. Следовательно, Зло— 1 = п о —1, откуда яо = 0, что невозможно, так как](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-138-320.jpg)
![по — натуральное число; б) у к а з а н и е : / (х) = 1 только при х = 0, это сле
дует из иррациональности -у2. С—9. 2. [2; 3]. 3. Плюс. С— 10. 2. Решение.
л л _ л л л л ,
sin , поэтому cos sm — -> co s — , a c o s — > sin cos — (так как x > s m x,
где x — cos-y-)- 3. М ножество всех действительных чисел, кроме чисел вида
, k£Z. С— 11. 1. D (/) совпадает с D (tg) £ (/)— (0; 1]. 3. tg 5; tg:2;
tg 10; tg 7. С — 12. 1. a) 0,96; б) З л — 10. 2. Р е ш е н и е . ■— — arcsin xg[Q; л] и
cos — arcsin x^ = s in (arcsin x) = x. 3. a) — 0,8223; 6) 0,8025. С— 13.
Л Jlk л zzk
а) ( — l)t + 1т п + т г • k£Z] б) -Г5-+ - 5- , k ^ Z . У к а з а н и е . Уравнение приводится
12-; 2 1x5 о
к виду tg Зх—~ , после решения которого, надо проверить, что при получен-
л/з
л it Ttk~ ( 9л
ных значениях определены t g x и tg 2х; в) 42 ± ;'д ‘ + _з ' • kZ Z . С— 14. а) f —
tS+"*) ;(Й+^;т +лк) ' ( т +лй: ш +лк) :{т£+л*;й +л*) -*е2-
У к а з а н и е . Неравенство приводится к виду tg ( х - Ь - ^ < - 4 . после решения
L 5Я , и Л ,которого из полученного множества надо исключить числа вида — + як, ~у~г
+ л к , при которых не определен t g^ 3xH— или tg 2х; б) + ,
* 6Z. С— 15. а) хо~-—у , ftgZ, x0= y a rc tg ( — ^ « . —0,58; б) — ^- + 2лк
( - l f ^ + л к , k £ Z . С -1 7 . ( ( — I)4 -g -+ „ n ; ( - l ) * J L + f 0 С -1 8 . 1. а) 1; 3;
б) не существует; 1; в) ( — 2; 2] и точка 3. 2. 0,39. С — 19. 1.а) 2,5; б) 6. 2. а) 4;
3
б) — . С—20. 1. Второе больше (в обоих случаях). 2. Зх2— 4хо + 4+{Зхо — 2) Дх +
+ Дх2; Зхо —4хо + 4. С—21. а) 4=.— Зх2; б) -— Ц , . С—22. 1. а) 2 - л [ х -
, л/х (х ~ Н 2
1 Sjc -1-9г
—— 5.4*17; б) —— . 2. 0. У к а з а н и е . /( * ) = * х и / ' (0) =
2 -Д* 2 у х
— lim — — - — lim lim k l = 0 (так как функция g -(* )= U j непре-
Xr-^ 0 X х-*-0 X х-»-0
рывна в точке 0). С—23. а) ± 2 ; ( — оо-; — 2)U(2; оо); ( — 2; 2); б) 0; (0)1);
( — оо; 0)U(1; <»)• С —24. 1. а) ( —л/П ; —л/7)U(л/7: л/ГТ); б) [4; оо) и точка 0.
2. fn (х)— 1— — при ri = 3k — 2, f„ (х )= — * t при ti — 3 k — , f„{x) = x при /г— Зй,
*€Л7; D (/) = ( — оо; 0)U(0; оо); D (/„) = ( — оо; 0)U(0; 1)U(1; °°) при п^=2. 3.
а) — ----; б) 27 ( х 2— 4 V *) (*3—^ V*)8- С—25. а)5 cos 5х; б) 0 при
2.л/Зх?-1-2х2- 12 V 2 /
xZD(J) в) З-у’г з ш 4 x s in (2 x — . С—26. 1. При 0 < а < 4 . 2. a) [—V2; — 1]U
и ( - Т ; т ) и (1 :^ ); б) ( _ 4 ; — 3)U( — 2.5; - 2 ) . С -2 7 . 1. 2. у =
= _ L _ 4 ? j x - Л). С—28. 1. 1,012. 2. 0,9009. С—29. 1. 4с; 2 1 — . 2. Р е ш е н и е .
у/2 6 с
135](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-139-320.jpg)
![S' (0= - 7 7 ^ W '' * ' ( 0 = Л а ; f = m 0s "(0 =
6т 0
(t—2)3 ’ " w _ (<-2)4’ 4V_(<-2)4 -
= 6mos2 (1). С —30. 1. Возрастает на ( — оо; оо). 2. х =
= — 4 + л^. ^ 6 ^ ,— точки максимума; х = -^ - + лй, ft£Z,—
о о
точки минимума. С —31. Убывает на (— оо; 1) и н а |^ ^ I °°у .
возрастает на 1 х = ~ ^ — точка максимума. С—32.
1. Возрастает на ( ~ " 001'[У > убывает на
x — j 2 — точка максимума. С—33. Убывает на (— оо; — 1],
возрастает на [— 1; оо); х = — 1 — точка максимума.
С—34. 1. max/ = / ( l ) = l ; m in / = / ( — 1 ) = — 1. 2. 3 м2.
R R
X co s ^ 2 / + - ^ . Р е ш е н и е . Х (< )+ х2 (0= 3 ^cos 2/ +
+ c o s ^ 2 < + - = 6 cos ( 2/ + - ^ c o s ^ - . 2. ± 3-/3.
С — 36. —Щ . 3. tg 7 5 ° = 2 + V 3 и cos 7 5 ° = ^ ~ л /2. С — 38. 1. а) | | ;
б) у . 2. а) k e Z , к ф 7 п (где я £ 2 ). K Z ; б) - J + y ;
Т + Т ;М+ Й ’ *€Z- 3- а) ( ~ т +2я*; Т +2я* ) ’ б) [ ~ Т +
+ 2я&; 2nftj ,j^^-)-2nfe; n + 2nfej , k £ Z . С—39. 1. a) (— 0 0 ; —8]U
U[-4;4]U[8; 00); 6) (3; 4). 2. a) ( - 2 ; - 1)U(2; 00); 6) ( - 0 0 ; - 7 ) U ( - 4 ; - 2 ) .
C—40. 1. a) — 4 — 4 — % J 6) -------- * — ; в) x2 sin x ; r) 66 (3x2— 2x) (x3—
X X X x2 Ух2-)- 1
—x2)65.2. (— oo; 0)U(2; 00). С—41. 1. y = 1 и y = — 8x + 9. У к а з а н и е . За
пишите уравнение касательной, проходящей через точку (хо; — Хо— 2хо). (Это
уравнение имеет вид у+Хо+2хо = (—2хо — 2) (х—х0), т. е. у = ( — 2х0—2) х+х§.)
После этого найдете х0 из условия у (1)= 1, откуда х0= — 1 или хо= 3. 2. а) 1,0004;
3
б) 0,5302. 3. — jg Н. С —42. 1. См. рис. 15. 2. Правильный.
Вариант 10
тг ТГ 4ТТ.
С— 1. 1. -£•; -£• ; 1L■; -Д.■. 2. а) — 144°; б) —4176°. 3. 40°; 65°; 115°; 140°; 2,4435.
о о о Ь 2
4. 89°28/; 139°43'. С — 2. 2. а); б) Минус. 3. 1—sin а ; 1-1—- . С—3. 1. 1. 2. cos 2а.
т/5
С -4 . 1. - - 1 . 2. - 1 ^ - 3 . - 2 sin22а. С -5 . 1. а) [1; 17)U(17; 00 ); б) [ о ; •
2. — 16; 9; 8; Зх2+ 5. С—7. 1. а) Убывает на ( — 0 0 ; y j , возрастает на ; оо^ ;
б) убывает на (— 0 0 ; — 1] и на [1; оо), возрастает на [— 1; 1] 2. Например,
136](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-140-320.jpg)
![У
5 7 "_ 4Т -Т 2 Т Т О
~3 3 ' з "з
Г / Г У Г У Г
Т 2Т Т 4 7 5 7
3 5 5 5
Рис. 16
a) f[x) = 2x, g ( x ) = x ; б) f{ x ) = x g (x) = 2x в) / ( х ) = 2 х + х ; g (х)= 2х;
г) f {х) = 2jc+ sinjc; g (x ) = 2x. С—8. 1. Рис. 16. 2. а) Зл; б) з. а) У к а з а -
О
н и е. Пусть 7 "> 0 — период функции. Тогда f(T )= f(0 ), поэтому Т имеет вид
Т — л 2п2, где n £ N , f (2 T )= f (Т) = 0, поэтому 2Т имеет вид л 2*2, где * 6Л Но
тогда 2л2п2= л 2*2, откуда ->j2— ~ , что противоречит иррациональности у/2. Другой
способ рассуждений: период не меньше расстояния между двумя соседними нулями
функции, а это расстояние (л2 (* + I)2— л 2*2= (2* + 1) л2) можно выбрать большим
любого наперед заданного числа Г > 0 (взяв достаточно большое к ) ; б) у к а з а
н и е . / (х) = 2 только при х = 0; это следует из иррациональности у/2. С—9. 2. [0; 8].
3. Минус. С— 10. 2. У к а з а н и е , cossin l > c o s l> s in c o s 1 (подробнее см. ре
шение вар. 9). 3. М ножество всех действительных чисел, кроме чисел вида
* 6 Z. С— 11. 1. D (/) совпадает с D (tg); £ ( / ) = [ — 1;1]. 3. tg 12; tg 9; tg 6; tg 3.
С— 12. 1. a) 0,28; б) 4 л — 10. 2. Р е ш е н и е . a r c c tg x = —— arctg х, поскольку
9906.ctg — arctg x^ = tg a r c tg x = x и 0 < -^ - — arctg x < n . 3. a) 0,7622; 6) 0;
C -1 3 . a) ( - l ) ‘+ ' 4 + ^ , *gZ ; 6) - У + n k , ^ + лk, * 6 2 . У к а з а н и е .
О 2 12 12
Уравнение приводится к виду tg З х = — 1, из множества решений которого (это
31 I пп п , яп
множество чисел вида — ’ п ^ ' надо исключить числа вида ~ —-— ,
n £ Z , при которых не определен tg 2х, и проверить, что при полученных значениях
1 г; П 1 n k Я t Zlk ЗЛ , Jlk . _ _
определен tg 5х; в) g j + ^ g . k £ Z . С -1 4 , a) ; 2 8 + ~ 2 / ’ 6 ’ У К а '
з а н и е (см. указание к вар. 9); б) |^ - + я*; ^ + n*J , * 6 2 . С— 15. а) у + 2я*;
. 5я , „ , , л , 2л* „ / я , л/г я , я* ,
± -g - + 2n*, * €Z; б) 2л*; -g--|— g- . С— 17. ^ л я ; - ^ - + - < r + n n )>
« 6 2 . С— 18. 1. а) 0; 0,5; б) не существует; в) ( — 1; 2,5) и точка 3. 2. 0,36.
7 1
С — 19. 1. а) — ; б) 10. 2. а) ; б) —42. С—20. 1. Первое больше в обоих слу
чаях. 2. Зхо + 4*о — 5 + (Зхо + 2) Дх + Дх2; 3xo-f*4xo — 5. С—21. а) 2 х ;
1 1 5 ^
б) - Т - - а . С - 2 2 . 1. а ) - - ---- — + 1 0 U 100; б) 7,5л:у/х-3,5х*-фс. 2. 0.
4 х ^ х 2-yJx
У к а з а н и е , f (х )= х 2х и / ' (0 )= lim ^ ^ — lim хх — 0. С—23. а) — 2
Jt-vO х х-*-0
и 1; ( —оо; —2) и (1; оо); (—2; 1); б) - З и —1; ( —3; —2) U(— 2; —1); ( —оо; — 3)U
137](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-141-320.jpg)
![U(— I; оо). С—24. 1. a) (--*/5; -2 ]U [2 ; у/5); б) [1; оо) и точка 0. 2. /„ (*) = j------
X — 1
при n — 3* — 2; U {x)— —^r~ при n = 3 k — 1; f„ (x )= x при n = 3 k , k £ N , D (/) =
= ( — oo; 1)U(1; оо); О (Jn)— ( — оо; 0)U(0; 1)U(1; оо) при n ^ 2 . С—25. a) — 5 sin 5*;
6) — . ; в) —4x sin (4x2—6) cos2 (2x? — 3). C -2 6 . 1. При a > 2,25. 2.
sin (2* -f-2)
a) ( - o o ; - 2 ) U ( - V 2 ; - 0 , 5 ] u [ y ; V 2 )u (2 ; °o); 6) (2; 2.5)U(3; 4). C -2 7 . 1.
(M 3) ‘ + T - -
. C —28. 1. 0,9976. C—29. 1 .7 c; 23,5 — . 2. P e in e-
12 с
и и e. s' (/)= —
(21-1)'
16
F = moa-
16m0
(2/ —1)'
= 2m 0s 3 (t).
3-V3 .C —30. 1. Возрастает на ^ — oo; ^ з ^ ~ ] и lla | * ~ • 00 ) ■убывает на
• 2. х = я£, fcgZ,— точки минимума; х = - ^ - + л к , k £ Z ,— точки макси
мума.С—31. Возрастает на ^ — ° ° ; — 4 и на ( — 2; оо), убывает на
—4 - i - ; — 2 ^ ; х — — 4-^ точка максимума. С —32. 1. Возрастает на
^ - оо; — j , убывает на £ — ' ° ° ) ’ х ~ — ^ ~ точка максимума.
2 р — 2 ^3 _ 3 + 2V 3) ^ у (х) _ 2 [х— 1)2> 0 при х ф , поэтому / возрастает
на ( — оо; 1], в частности, f ( x ) < f ( t) = - |- при х < 1 . С—33. Убывает на ( — оо; — 2)
и на [2; оо), возрастает на ( — 2; 2]; х = 2 — точка максимума. С —34. 1. D (/) =
= [ - 2 ; 1], ш ах / = / ( - 0 , 5 ) = 1,5; min / = / ( —2) = '
[-2: 1] [-2; 11
= f ( l ) = 0. 2. 40 см.У к а з а н и е . Обозначим боль
шее основание через 2х. Тогда Л = У 2 02—(10— x f =
= У 3 0 0 + 2 х -л г !; 5 (x)==2 f ± 2 2 A = (x + 10).y300 + 2 0 * -
.S' (*) = 400 + 2* ,...? £ L и S '(^ ) = 0 при дсг= 20. Д алее,
у з о о + 20* - +
D (S) = [10; 30], S (20) = 300УЗ > S (10) = 400, S (30) = 0.
Чя
С—35. 1. 2 cos — cos
о
2. 0. Решение.
x(t) = 2 cos (51 + <р), при этом х(0) = 2, т. е. c o sq > = l.
Д алее xf (t)= — 10 sin (5/+<р) и xf (0 )= — 10 sin <p=0.
-|^ .3 .tg l5 ° = 2-y3; -cos.5° = - ^ ± ^ .C—36. 1.
С —38. I. a> i g ; б) Y . 2. a) 2nk, AgZ; б) . як, k £ Z .
3. a) ( - i + 2nft; Y + 2 afe), k £ Z ; 6) | - + 2лй; y +
+ 2 n k , ] ^ + 2nk у + 2jia] , k £ Z . С —39. 1. a) [ - 6; -2 ]U
U[2; 6i 6) ( - oo; 0)U(0; 3>U(5; oo). 2. a) ( - 2 ; 0)u[-|; 2) ;
138](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-142-320.jpg)
![Ч 4 Ч 1 -4- Ч г 2
б) ( - 3 ; —2)U(— 1; оо)- С -4 0 . 1. а) - 4 + 4 - 4 ; б) г ‘; * - ■; в) *2Х
х х х У х (1— х2)2
X cos х; г) 42(4х3— Зх2)(х, — х 3)4'. 2. [— 1; 0)U(0; 1]. С—41. 1. у = и i / = — 8х — 7.
2. а) 1,0016; б) 1,1047. С —42. 1. 3. У к а з а н и е . Функция f{x) = x 3— 9 * + 1 0
возрастает на промежутках ( — оо; — ^3], [УЗ; оо), убывает на промежутке
[— [3^[3] (рис. 17), поэтому она имеет на каждом из этих промежутков не
более одного корня. При этом корень существует на каждом из этих промежут
ков, так как функция непрерывна и, например, / ( * ) < 0 при больших по модулю
отрицательных х, a f ( —-у 3 )> 0 . 2. Правильный.
П р о в е р о ч н ы е р а б о т ы
П Р — 1. Вар. 1. 1. 0,6; — 0,8; sin я = 0; cos я = — I; sin (— 630°)= 1.
2. у см. з, ± у * . 4. 0. 6. Минус. 7. Например, /(х ) = х3. 8. 0,75. 9. 0. 10. 2.
Вар. 2. 1. у ; у ; t g y = l ; c t g y = l ; ctg ( —450°) = 0; tg 5 4 0 ° = 0 . 2. 2,45 м2.
3. ± 4 - - 4. 5 sin a cos а (т. е. 2,5 sin 2а). 6. Плюс. 7. Например, / ( х ) = х 2.
У3 ,—8. 2,7. 9. У0,1 . 10. 2 cos (р — a )c o s(P + a).
П Р — 2. Вар. I. D (/) = (— оо; оо); Е (f) — (0; 1]. 2. Убывает на ( — оо; 1],
возрастает на [1; оо). 4. Возрастает на ( — оо; оо), экстремумов нет. 5. sin 4;
sin 6; sin 2. 6. а) ~ ; б) я. 7. а) 0; б) 1. 8. л; 9. а) 4 + 4 . &€Z;
3 о 1о 2
б) - 2 ± у + 4 л * , kez. ю . а) ( у + у ; т + т ) ’ ft€Z; б) _ т + 2л*> fefEZ
11. ( J ^ + nk + nri; —^ + л й — я n j ^ —- ^ + л £ + я л ; —^ + л£ — лл^ , £gZ ,
n(:Z. Вар. 2. 5. х = — -^r+ n k, k £ Z ,— точки максимума; x = ^ + nk, &6 Z ,— точ-
1и о
ки минимума. 6. а) 4л; б) л. 7. — . 8. а) Д а; б) нет. 9. 4-{-( — 1)*
. 4 Ь о
A+Z; б) ± у + у . b t z . 10. а) ( _ у + 2лк; у + 2л* ) , *£Z ; б) ( - у + у ;
у + у ] , 11- ( у + 2лк-, у -2 л й ) , *gZ.
ПР — 3. Вар. I. 1. а) ( — oo;0,5]U [l; <»); б) (— 1,5; 1)U(2; 4). 2. 1/ = — 4х — 4.
3. 9х2— 9х; - 4 - sin 4 — 2 cos 2х. 4. а) (12/3—6#*)— ; (3612— 1 2 1 )4 . 5. З х + 2 ;
, С С 2У х+ 1
2,75. 6. 2 2 , 0 3 . 7. Убывает на [0; 1], возрастает на [1; оо). 8. х — — точка
32 3
максимума; х ~ — точка минимума. 9. Возрастает на ( — оо; — 1] и на [1; оо),
убывает на [— 1; 1]; х = — 1 — точка максимума; х = 1 — точка минимума.
10. min f = f (2) = 4; гтшх / = / (1 )= 5 . И . у " = — 3у. Вар. 2. 1. а) ( — оо; 0 ] ll[ y - ; ° ° ) ;
б) ( оо; 3)(J( 1; 2)U(6; оо). 2. « /= 1 2 х -1 9 . 3. 5 х - 5 * 4; _ 2 + ^ —
COS Z a . п X
Sin2 у
1 о __ у
4. а) 8/3— 1; б) 63 р ад/с; со(1)= 0 при t — -^ -. 5 .-------- - ; 0. 6. 600х2 (2х3— 1)"
2 2 х 2 У х — 1
139](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-143-320.jpg)
![7. Возрастает на R . 8. х = 0,25— точка максимума. 9. Возрастает на (— оо; —2]
и на [0; оо), убывает на [—2; — 1) и на (— 1;0]. !0. а) 12+ 0; б) 6 + 6.
11. у = A cos (0,5х + ф).
П р и м е р н ы е к о н т р о л ь н ы е р а б о т ы
К— 1. В а р , 1. 1. а) —- у ; б) - Щ - в) 2. а) - 0 ,8 ; б) - Ц М .
4. т 2— 1; У2. В а р . 2. 1. а) — 0,5; б) - у ; в) — УЗ. 2. а) 4 ; б) -—
4. 1 - л 2; -л /2 . В а р . 3. 1. а) — Д б) в) Щ . 2. а) -0 ,6 ; б) - 7 . 4. р = - 2 ,
n €Z. В а р . 4 . 1. а ) ^ ; б) - 0 ,5 ; в) у . 2. а) -0 ,8 ; б) - 7 . 4. р =
^ "У3
= х + 2, х ф 2 , х ф - ^ п , n £ Z .
К—2. В а р . 1. 1. [ - 2 ; 3)U(3; оо). 2.0,5. 5. [о; у ) ( j ( y ; у ) и ( у ; &]■ В а р . 2.
1. [- 0 ,5 ; 2)U(2; оо). 2. 1,5. 5.[ - 4 ; - я ) 1 1 ( - я ; 0).В а р . 3. 1. ( - оо; 0)U(0; 1].
2 . ^ . В а р . 4. 1. ( - о о ; —3)U( —3; -1 ] . 2. -1 ,5 .
я 2л
К—3. В а р . 1 . 1. а) — —+ 2лл, n £ Z б) 2лл, ± у + 2 л л , n £ Z ; в) ял,
— -7-+ ЛЯ, n£Z. 2. — ^- + 2 л л ^ х < 4 + 2ял, a£Z. 3. ( — ^- + 2лл; 4 —2ллУ
о 6 6 4 4 /
n£Z ; ^ —у + 2 л £ ; у — 2nk^ , k £ Z . 4. 2лл =£(х л + 2лл , a£ Z . Вар. 2. 1. а) л +
+ 2лл, n£ Z ; б) у + 2лл, (— 1)"+ | у + лл, a(EZ;в) у + лл, у + лл, n £ Z .
2. у + 2 л л ^ х ^ у + 2лл, ngZ. 3. + 2ял; у — 2лл^ , n£Z; ^ — у + 2лк
у —2лk j , ftigZ. 4. у + 2лл < + < у + 2лл, п 6 Z. Вар. 3. 1. a) ( — l)" у + лл, л £Z;
б) я + 2лл, ± у + 2лл, a£Z; в) —у + лл, arctg 3 + лл, agZ. 2. — ^ - + л л ^ х <
< 4 г + я л > n£Z. 3. ( 4 л + 2лл; — л —2лл ), ngZ. 4. —4 + 2 я я ^ х ^ 4 г +
2 4 4 / 6 6
+ 2яя, ngZ. Вар. 4. 1. а) ± у + 2лл, ngZ; б) —у + 2ля, (— 1 ) " у + ля, n£Z;
тг я л / Зл
в) у + л л , —arctg 2 + лл, ngZ. 2. — —+ ял < х г ^ у + лл, n£Z. 3. +
+ 2 ял; 4 + 2 ллУ n £ Z . 4. —^ + 2 я я < л : < ^ + 2яя, agZ.
4 / 3 3
6 3
К—4. В а р . 1 . 1. 1,56. 2. а) х2+ 2х + 2; б) —у — ^л/х; в) g ' (х)=4 cos х,
g ' ( - y ) = - 2 ; г) А ' ( х ) = - £ - р ] , ; А' ( 1)= 8. 3. 2. 4. / ' ( * ) - - |х|.
/ ' ( 0) = 0. Вар. 2. 1. 1,12. 2. а) - 2 * 2+ 4 х - 1 ; б) - ) ^ + y V x ; в) g ’ (х)=
= —3 sin х, g ' ( - ^ ) = l,5; г) А'(х) = - ^ 4 _ 5; Л '( 1 ) = - 7 . 3. 3. 4. /'(*) =
= 4 |х|, Г(0) = 0. Вар. 3. 1. 5,25. 2. а) 2х2- 2 х - 7 ; б) - 4 r + - | j = : в) g ' (х)=
хх З у х
140](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-144-320.jpg)
![- s h ' « ' ( ~ т ) - 4; г) * 'и - 5 Т з ? ' 3- 4- «• гМ -л 5 = Т
4 3 4 / 2лЛ
Вар. 4 1.2,78. 2. а) - * 2+ 8* + 2; б) в) * ' (*) = , г ' ( ~ т ) =
= - 5 у ; г) Л 'W = - ( ^ j 5. Л '( 4 ) = - 1 3 . 3. 2. 4. * ( * ) = У ? + 2 .
К—5. Вар. /. 1. (— с» ; — 3)U(3; 5). 2. 6 см/с. 3. - j - . 4. у = 2х. 5. ( — оо; — 1];
х = 1 . Вар. 2. 1. (— 5; — 2)U(2; оо). 2. 8 см/с. 3. - j - . 4. у — — 2 х — 2. 5. [0; 5];
х = — 5. Вар. 3. 1. ( — оо; — 1,5]U[1; 5). 2. 36 см /с2. 3. — . 4. у = 2 х — 4. Вар. 4.
1. [ — 3,5; 2]U(4; оо). 2. 36 см /с2. 3. у . 4. у = - 2 х - 4 .
К—6. Вар. /. 1. Возрастает на ( — оо;0] и [2; оо); убывает на [0; 2]; х = 0 —
точка максимума; х = 2 — точка минимума; f(0) — 4, / ( 2) = 0. 2. Слагаемые 8 и 4.
4. —6 ,3 < ! ф '( д :К — 2,3; ф '(л:)<;0 для любого действительного х. Вар. 2. 1. Убы
вает на ( — оо; 0] и [2; оо); возрастает на[0; 2]; х = 0 — точка минимума;
х — 2 — точка максимума, /( 0 ) = — 4, / ( 2) = 0. 2. Слагаемые 6 и 3. 3. х" =
= —4лг. 4. 1,2sg;/' ( х ) ^ 5,2; f (х) > 0 для любого действительного х.Вар. 3.
1. Возрастает на (— о о ; —2] и [2; оо); убывает на [— 2; 2]; х — — 2 — точка
максимума; х = 2 — точка минимума. / ( —2) = 2-^-, / ( 2 ) = — . 2. Слагаемые
О о
6 и 2. 3. У ' = —4х. 4. Уравнение имеет один корень, если с > 2 ~ - или с < — 8-^-;
о О
два корня, если с — 2-^- или с = —8-^-; три корня, если — 8-^- < с С 2 -j-. Вар. 4.
О о о о
1. Убывает на ( — оо; — 2] и [2; оо), возрастает на [—2; 2J, х — 2 — точка макси
мума; х = —2 — точка минимума, / ( —2 )= — 2 -r-, f (2) = 8-5-. 2. Слагаемые 9 и 3.
О О
3. Например, при А = 1, ф = 0, y = cos It. 4. Уравнение имеет один корень, если
т > 8-^- или т < — 2-^-; два корня, если т = 8-^- или т — — 2-^-; три корня,
если —2- ^ - < m < 8- i - .
К—7. Вар. 1. 1. а) | + | л , « € 2 ; б) ~ + | я , n € Z. 2. - 2 . 3. а) - - £ • +
+ 2ля < х < - ^ - + 2 л п , ng Z ; б) ( — 00; 0]U[2; 4). 4. Возрастает на ( — оо;0] и
[2; оо), убывает на [0; 2]; х — 0 — точка максимума; х = 2 — точка минимума,
/ (0 )= 1 -i-, f(2 )= 0 , 0 < f ( r ) < l - |- , если — l ^ x ^ 3 . 5. х2+ х + 1 > 0 для всех х,
О О
поэтому 4Х2— 9 < 0 , — 1 ,5 < л г< 1,5, c o s x > 0 . Вар. 2. 1. a) « 6 2 ;
б) | + | n , ng Z . 2. 1. 3. а) -^- + 2 л п < х < ^ + 2лп, n £ Z б) ( — 1;0]U[4; 00).
4. Возрастает на (— оо;0] и [1; оо), убывает на [0; 1]; х = 0 — точка макси-
1 2
мума; х — 1 — точка минимума, f (0)= — 1— , / ( 1) = — !— , —3 < / ( х ) ^ 0 , если
о О
— 1 ^ х ^ 2 . 5. х 2—х + 1 > 0 для всех х, поэтому х 2— 3 х < 0 , 0 < х < 3 , s i n x > Q .
Вар. 3. 1. а) ± ~ + лп, n £ Z б) —^ + «■ « 6 2 . 2. — I. 3. а) ^р + 2 я п ^ х <
5Я
+ 2лл, n g Z ; б) ( — 1;0)U(0; 1)U(3; оо). 4. Возрастает на (— оо;0] и [1; оо),
141](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-145-320.jpg)
![убывает на [0; 1]; * = 0 — точка максимума; х = 1 — точка минимума, / ( 0 )= 5 ,
/(1 ) = 4. Корень уравнения — 1. 5. х2+ 1 > 0 для всех х, поэтому х —5х + 6 < 0 ,
2 < х < 3 , 1 < -^ -< 1 ,5 , s in -^ -> 0 . Вар. 4. 1. а) ± - ^ - + л л , n £ Z б)
n£ Z . 2. — 2,5. 3. а) ^ + 2лл + 2лп, n £ Z ; б) ( - оо; — 3)U(— 1; 0)(J
U(0; 3). 4. Убывает на ( — оо; — 1] и [1; оо), возрастает на [ — 1; I]; х = — 1 —
точка минимума; х = 1 — точка максимума, / ( — 1 )= 0 , /(1 ) = 4. Корни уравне
ния — 1 и 2. 5. х* + 3 > 0 для всех х, поэтому х3 — 10х + 2 4 < 0 ; 4 < х < 6 ;
2 < - |- < 3 ; c o s -^ -< 0 .
М а т е р и а л д л я и т о г о в о г о п о в т о р е н и я
Вариант 1. 1. -^- + лл; + 2 л п , n £ Z . 2. —- ^ + cos 2х. 3.
U ^ -^ -;3 j. 4. ( — оо; — 2)U[0; 3). 5. х = 0 — точка максимума, у ( 0) = 0; х = 2 —
точка минимума, у ( 2 ) = — 4. Графики имеют три общие точки.
Вариант 2. 1. —^ + 2 л л < х < - ^ + 2лл, n £ Z . 2. —-^--f sin 0,5х. 3. у =
= Л cos (5/ + <р). Например, у = cos 51, у = 2 cos ^ 5 / + - ^ . 4. ( — оо; — 5)U(0; 3].
5. max y = i/(3 )= 2 1 , min у = у { ) = .
- и— oo;3)U (3; оо). 3. sin х. 4. Объединение трех прямых:
у — 1, х = 6, х — — 3. 5. х = 0 и х — 2 — точки минимума, f( 0 ) = f( 2 ) = 0 ; х = t —
точка максимума, / (1) ===4.
Вариант 4. 1. — 2. 2. 120 см/с, 168 см /с2. 3. — cos х. 4. х = 0 и х = 4 —
точки минимума, f(0) = f(4) = 0; х — 2 — точка максимума, / (2) = 4. 5. +
+ 2лл; — ^— 2л л ^ , n ^ Z .
Вариант 5. 1. tg а. 2. — arctg 4 + лл, ~ + лп, n £ Z . 3. — 12. 4. (— 8; —3)U
U(3; оо). 5. Возрастает на каждом из промежутков (— оо; — 1] и [1; оо), убы
вает на [— 1; 1]; х = — 1 — точка максимума, / ( — 1)= 8; х = 1 — точка мини
мума, / ( 1)= 0.
Вариант 6. 1. 1. 2. у = 2х — 8. 3. ( — оо; — 1]U(2; 3]. 4. arctg 3 + лп, — ^- +
+ лл, n£ Z . 5. Возрастает на каждом из промежутков [— 1; 0] и [1; оо), убыва
ет на каждом из промежутков ( — оо; — 1] и [0; !]; х = — 1 и х = I — точки ми
нимума, / (— 1 )= /(1 1 = 2; х = 0 — точка максимума, / ( 0 )= 3 .
24
Вариант 7. 1. —— . 3. — 1. 4. а) ( — оо; 2)(J( — 2; 2)U(2; оо); б) возрастает
на каждом из промежутков [1; 2) и (2; 4]. 5. Слагаемые 24; 12; 18.
Вариант 8. 1. — I- Возрастает на каждом из промежутков ( — оо; — 1]
и [1; <*)"■ убывает на [— 1; 1]. 3. ~ - - 2 л п , ( — 1)'1 + |-^- + л л , n£ Z . 5. Слагаемые
16, 16, 16.
Ь Н fВариант 3. 1. 2. 2. Г
142](https://image.slidesharecdn.com/algebra9klass-150908130547-lva1-app6892/85/9-146-320.jpg)



