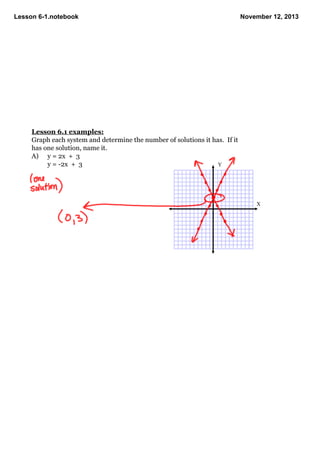
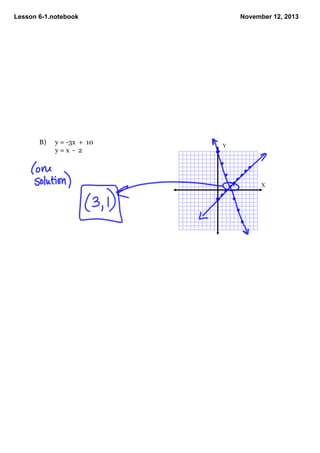
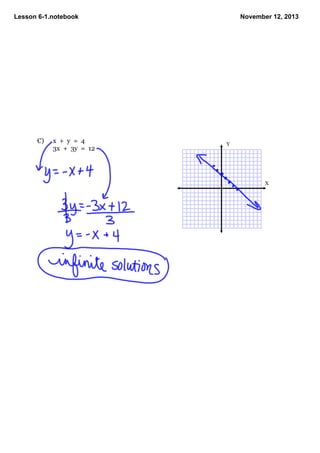
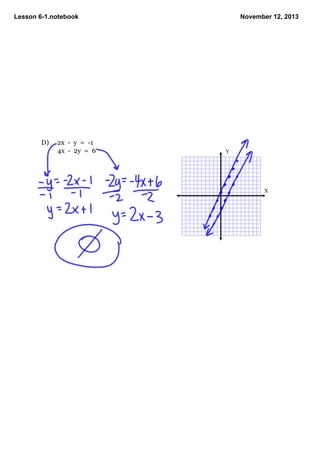
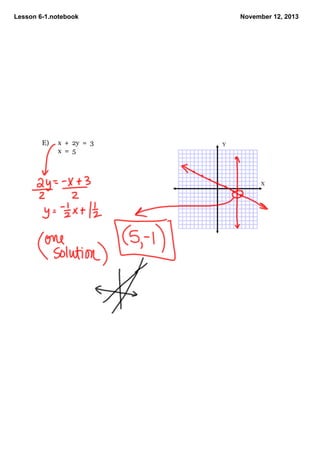
This document contains notes from a math lesson on solving systems of linear equations and inequalities. It includes examples of solving compound inequalities and graphing systems of equations. Key points covered are: systems can have one solution, infinite solutions, or no solutions; if they have one solution they are consistent and independent; if they have infinite solutions they are dependent; if they have no solution they are inconsistent. The lesson concludes with examples of graphing different systems of equations and determining the number of solutions.

1. Lesson 6­1.notebook
November 12, 2013
Assignment:
1­­>L6.1, pg. 336­337, #16 ­ 24 (evens) & #28 ­ 40 (evens) ­ Due THURSDAY (11/14)

2. Lesson 6­1.notebook
November 12, 2013
Lesson 6.1 WarmUp:
Solve each inequality.
1) ­2x + 4 > ­6
2)
5n ­ 3(n ­ 6) > 0
3)
23 ­ t < 2(t ­ 9) ­ 3(t + 2)
Solve each compound inequality. Then graph the solution on a number line.
4) m + 3 > 5 and m + 3 < 7
5)
­n > 2 or 2n ­ 3 > 5

3. Lesson 6­1.notebook
November 12, 2013
Lesson 6.1:
*FYI...the solution for a system of equations is the ordered pair that is a solution for
all of the equations....
...and... systems of equations can have one solution, an infinite number of solutions,
or no solutions....
**IF the system has one solution, it is called consistent. [the graphs intersect at
one point or are the same line]
***IF the consistent system has EXACTLY one solution, it is called independent.
[the graphs intersect at exactly one point]
****IF the consistent system has an INFINITE number of solutions, it is called
dependent. [the graphs are the same line(s)]

4. Lesson 6­1.notebook
November 12, 2013
*****IF the system has no solution, it is called inconsistent. [the
graphs are parallel]
­­>Look at the Concept Summary chart on page 333 in your
book!
ONE way to solve a system of linear
equation is to GRAPH them!

5. Lesson 6­1.notebook
November 12, 2013
Lesson 6.1 examples:
Graph each system and determine the number of solutions it has. If it
has one solution, name it.
A) y = 2x + 3
y = ­2x + 3
Y
X

6. Lesson 6­1.notebook
B)
y = ­3x + 10
y = x ­ 2
November 12, 2013
Y
X

7. Lesson 6­1.notebook
C)
x + y = 4
3x + 3y = 12
November 12, 2013
Y
X

8. Lesson 6­1.notebook
D)
2x ­ y = ­1
4x ­ 2y = 6
November 12, 2013
Y
X

9. Lesson 6­1.notebook
E)
x + 2y = 3
x = 5
November 12, 2013
Y
X