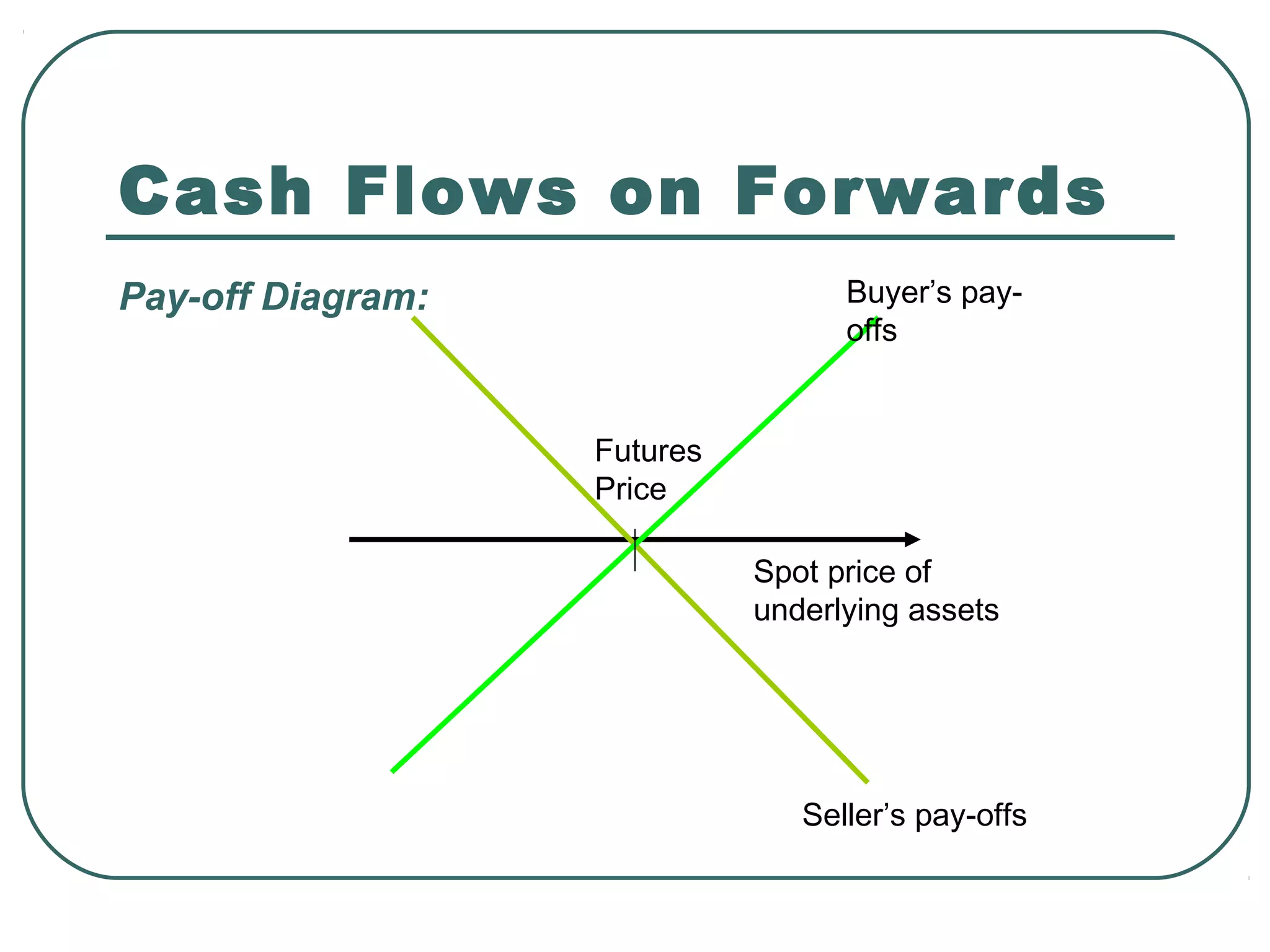
Futures and forwards are contracts that require deferred delivery of an underlying asset or cash settlement at a future date. A future is traded on an exchange and has standardized terms, while a forward is a customized over-the-counter contract. Forwards are useful when futures do not exist for a commodity or financial or when standard futures terms differ from needs. Euro-rate differentials futures contracts are tied to interest rate differentials between currencies and used to hedge currency exposures. Foreign exchange agreements allow hedging of exchange rate movements through a single cash settlement without a currency swap.

1. Futures and Forwards
A future is a contract between two
parties requiring deferred delivery of
underlying asset (at a contracted price
and date) or a final cash settlement.
Both parties are obligated to perform
and fulfill the terms. A customized
futures contract is called a Forward
Contract.

2. Cash Flows on Forwards
Pay-off Diagram:
Spot price of
underlying assets
Seller’s pay-offs
Buyer’s pay-
offs
Futures
Price

3. Why Forwards?
They are customized contracts unlike Futures
and they are:
 Tailor-made and more suited for certain
purposes.
 Useful when futures do not exist for
commodities and financials being
considered.
 Useful in cases futures’ standard may be
different from the actual.

4. Futures & Forwards
Distinguished
FUTURES FORWARDS
They trade on exchanges Trade in OTC markets
Are standardized Are customized
Identity of counterparties is
irrelevant
Identity is relevant
Regulated Not regulated
Marked to market No marking to market
Easy to terminate Difficult to terminate
Less costly More costly

5. Important Terms
 Spot Markets: Where contracts for
immediate delivery are traded.
 Forward or Futures markets: Where
contracts for later delivery are traded.
 Both the above taken together constitute
cash markets.

6. Important Terms
 Futures Series: All with same delivery
month with same underlying asset.
 Front month and Back month.
 Soonest to deliver or the nearby contract
 Commodity futures vs. financial futures.
 Cheapest to deliver instruments.
 Offering lags.

7. Important Terms
 Variation Margin
 Deliverables
 Substitute for Future Cash Market
Transactions
 Settlement in Cash

8. Interest Rate Futures
Two factors have led to growth:
 Enormous growth in the market for
fixed income securities.
 Increased volatility of interest rates.

9. Futures & Risk Hedging
 Interest Rate Risk
 Exchange Rate Risk
 Commodity Price Risk
 Equity Price Risk

10. Hedging Interest Rate Risk
A CFO needs to raise Rs.50 crores in February
20XX to fund a new investment in May 20XX, by
selling 30-year bonds. Hedge instrument
available is a 20-year, 8% Treasury -bond based
Future. Cash instrument has a PV01 of
0.096585, selling at par and yielding 9.75%. It
pays half-yearly coupons and has a yield beta of
0.45. Hedge instrument has a PV01 of 0.098891.

11. Hedging Interest Rate Risk
Hence, FVh= FVc × [PV01c / PV01h] × βy
= 50 × [0.096585 / 0.098891] × 0.45
= Rs.21.98 Crores
If FV of a single T-Bond Future is Rs.10,00,000
then, Number of Futures (Nf) = 21.98/0.1
= 219.8 Futures

12. Hedging Interest Rate Risk
If corporate yield rises by 80bp by the time of
actual offering, it has to pay 10.55% coupon
semi-annually to price it at par. Thus, it has to pay
Rs.50,00,00,000 × 0.0080 × 0.5 = Rs.20,00,000
more every six months in terms of increased
coupons.
This additional amount will have a PV at 10.55%
= 20,00,000 × PVIFA5.275%, 60
= Rs.3,61,79,720 ≅ Rs.3.618 Crores

13. Hedging Interest Rate Risk
Since corporate yield increases by 80bp, T-Bond
yield will increase by 178bp resulting in an
increased profit on short position in T-bond
futures
= 22,00,00,000 × 0.0178 × 0.5
= Rs.19,58,000 half yearly, which has a PV
= 19,58,000 × PVIFA4,89%,40
= Rs.3,41,09,729
= Rs.3.411 Crores

14. Why Not perfect Hedge?
 PV01 provides accurate and effective hedge for
small changes in yields.
 PV01s of cash and hedge instruments change
at different rates.
 PV01s need to be recalculated frequently
(practice is every 5bps). This can change the
residual risk profile.
 Additional costs related to recalculations need to
be kept in mind.

15. A Transaction on the Futures
Exchange
.
Buyer Buyer’s
Broker
Futures
Exchange
3
Buyer’s Broker’s
Commission Broker
Futures
Clearing
House
Buyer’s Broker’s
Clearing Firm
Buyer’s Broker’s
Clearing Firm
Seller’s Broker’s
Commission Broker
Seller’s
Broker
Seller
1a 1b Buyer and seller instruct their respective brokers to conduct a futures transaction.
2a 2b Buyer’s and seller’s brokers request their firm’s commission brokers execute the transaction.
3 Both floor brokers meet in the pit on the floor of the futures exchange and agree on a price.
4 Information on the trade is reported to the clearinghouse.
5a 5b Both commission brokers report the price obtained to the buyer’s and seller’s brokers.
6a 6b Buyer’s and seller’s brokers report the price obtained to the buyer and seller.
7a 7b Buyer and seller deposit margin with their brokers.
8a 8b Buyer’s and seller’s brokers deposit margin with their clearing firms.
9a 9b Buyer’s and seller’s brokers’ clearing firms deposit premium and margin with clearinghouse.
1a
6a
7a
2a
5a
48a 8b
9a 9b
2b
5b
1b
6b
7b
Note: Either buyer
or seller (or both)
could be a floor
trader, eliminating
the broker and
commission
broker.

16. Exchange Rate Risk
Hedging
Currency hedge is a direct hedge and not
a cross hedge as in case of interest rate
risk hedging. Hence, a hedge ratio of 1:1
works very well.

17. Forward Rate Agreements
(FRAs)
FRAs are a type of forward contract wherein
contracting parties agree on some interest rate to
be paid on a deposit to be received or made at a
later date.
The single cash settlement amount is determined
by the size of deposit (notional principal), agreed
upon contract rate of interest and value of the
reference rate prevailing on the settlement date.
Notional principal is not actually exchanged.

18. Determination of Settlement
Amount
Step-1:Take the difference between contract rate and
the reference rate on the date of contract settlement
Step-2: Discount the sum obtained using reference rate
as rate of discount.
The resultant PV is the sum paid or received. The
reference rate could be LIBOR (most often used) or
any other well defined rate not easily manipulated.

19. Hedging with FRAs
Party seeking protection from possible
increase in rates would buy FRAs (party is
called purchaser) and the one seeking
protection from decline would sell FRAs
(party is called seller).
These positions are opposite of those
employed while hedging in futures.

20. Illustration
A bank in U.S. wants to lock-in an interest rate for
$5millions 6-month LIBOR-based lending that
commences in 3 months using a 3×9 FRA. At the time
6-month LIBOR (Spot Rate) is quoted at 8.25%. The
dealer offers 8.32% to commence in 3 months. U.S. bank
offers the client 8.82%. If at the end of 3 months, when
FRA is due to be settled, 6-month LIBOR is at 8.95%,
bank borrows at 8.95% in the Eurodollar market and
lends at 8.82%.

21. Illustration
Profit/Loss= (8.82-8.95) × 5 millions × 182/360
= - $3286.11
Hedge Profit/Loss = D×(RR-CR)×NP×182/360
= 1 × (8.95-8.32) × 5 millions×182/360
= $15925
Amount Received/Paid
= $15925/1.04525= $15235.59
Note: 8.95 × 182/360 = 4.525

22. Index Futures Contract
It is an obligation to deliver at
settlement an amount equal to ‘x’
times the difference between the
stock index value on expiration date
and the contracted value
On the last day of trading session the
final settlement price is set equal to
the spot index price

23. Illustration (Margin and
Settlement)
The settlement price of an index futures contract on a
particular day was 1100. The multiple associated is 150.
The maximum realistic change that can be expected is 50
points per day. Therefore, the initial margin is 50×150 =
Rs.7500. The maintenance margin is set at Rs.6000. The
settlement prices on day 1,2,3 and 4 are 1125, 1095,
1100 and 1140 respectively. Calculate mark-to-market
cash flows and daily closing balance in the account of
Investor who has gone long and the one who has gone
Short at 1100. Also calculate net profit/(loss) on each
contract.

24. Illustration
Long Position:
Day Sett. Price Op. Bal. M-T-M CF Margin Call Cl. Bal
1 1125 7500 + 3750 - 11250
2 1095 11250 - 4500 - 6750
3 1100 6750 + 750 - 7500
4 1140 7500 + 6000 - 13500
Net Profit/(loss) = 3750-4500+750+6000 = Rs. 6000
Short Position:
Day Sett. Price Op. Bal. M-T-M CF Margin Call Cl. Bal
1 1125 7500 - 3750 2250 6000
2 1095 6000 + 4500 - 10500
3 1100 10500 - 750 - 9750
4 1140 9750 - 6000 2250 6000
Net Profit/(loss) = -3750+4500-750-6000 = (-) Rs. 6000

25. Pricing of Index Futures
Contracts
Assuming that an investor buys a portfolio
consisting of stocks in the index, rupee
returns are:
RI = (IE – IC) + D, where
RI = Rupee returns on portfolio
IE = Index value on expiration
IC = Current index value
D = Dividend received during the
year

26. Pricing of Index Futures
Contracts
If he invests in index futures and invests
the money in risk free asset, then
RIF = (FE – FC) + RF,
where
RIF = Rupee return on alternative investment
FE = Futures value on expiry
FC = Current futures value
RF = Return on risk-free investment

27. Pricing of Index Futures
Contracts
If investor is indifferent between the two
options, then
RI = RIF
i.e. (IE-IC) + D = (FE-FC) + RF
Since IE = FE
FC = IC + (RF – D)
(RF – D) is the ‘cost of carry’ or ‘basis’ and
the futures contract must be priced to
reflect ‘cost of carry’.

28. Stock Index Arbitrage
When index futures price is out of
sync with the theoretical price, the an
investor can earn abnormal risk-less
profits by trading simultaneously in
spot and futures market. This process
is called stock index arbitrage or
basis trading or program trading.

29. Stock Index Arbitrage: Illustration
Current price of an index = 1150
Annualized dividend yield on index = 4%
6-month futures contract price = 1195
Risk-free rate of return = 10% p.a.
Assume that 50% of stocks in the index will
pay dividends in next 6 months. Ignore
margin, transaction costs and taxes. Assume a
multiple of 100. Is there a possibility of stock
Index arbitrage?

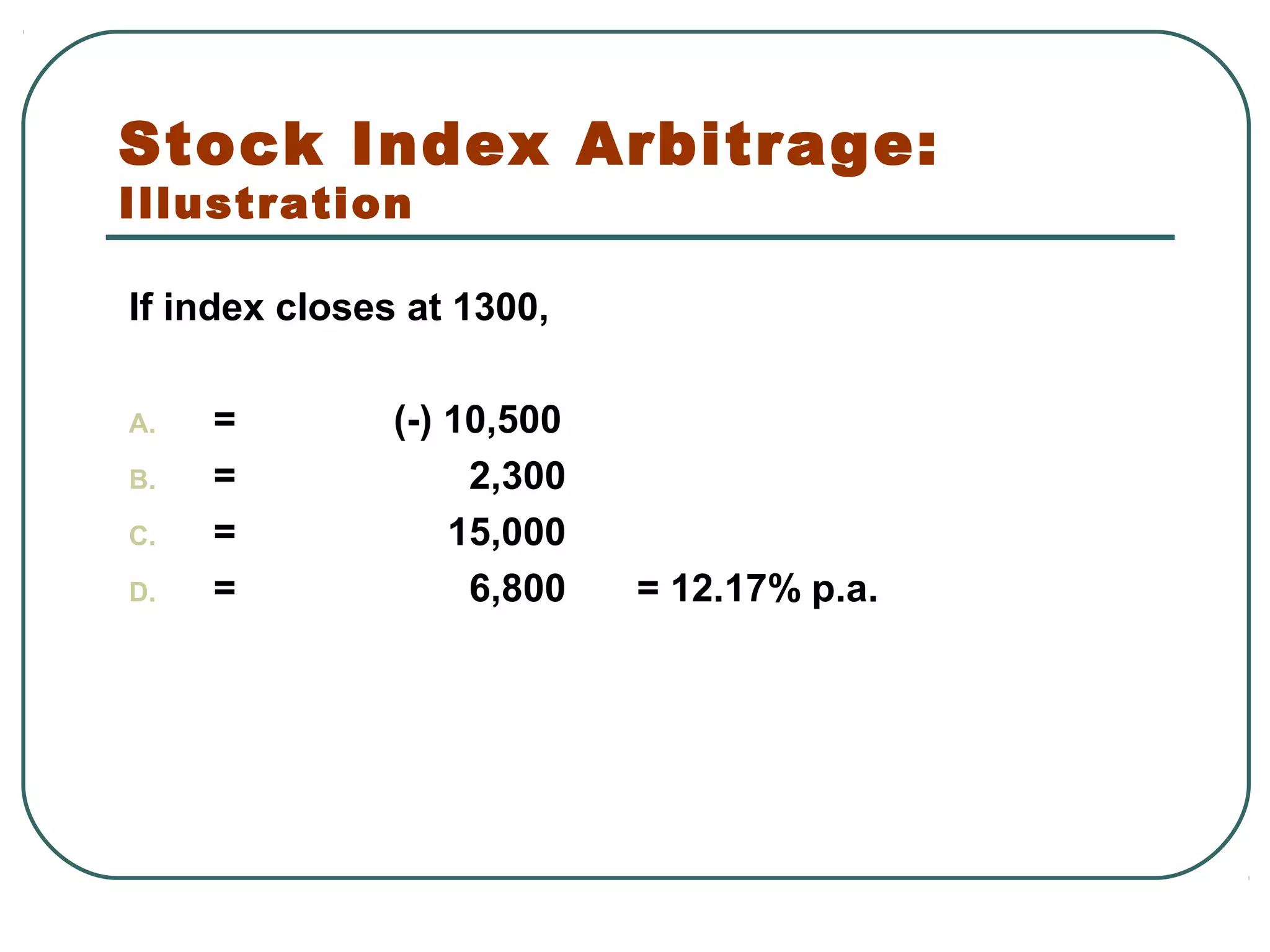
30. Stock Index Arbitrage: Illustration
Fair price of index future
FC = IC + (RF – D)
= 1150 + [(1150×0.10×0.5)-(1150×0.04×0.5)]
= 1150 + 34.5 = 1184.5 (hence it is overpriced)
Investor can buy a portfolio identical to index and
short-sell futures on index.
If index closes at 850 on expiration date, then
A. Profit on short sale of futures (1195 – 850) ×100 = Rs.34,500
B. Cash Div recd on port. (1150 × 0.04 × 0.5 × 100 = Rs. 2,300
C. Loss on sale of port. (1150 – 850) ×100 = ( - ) Rs.30,000
D. Net Profit = 34,500 +2,300 – 30,000 = Rs.6,800
E. Half yearly return = 6800 ÷ (1150×100)=0.0591 = 5.91%
F. Annual return (1.0591)2
– 1 = 0.1217 = 12.17%

31. Stock Index Arbitrage:
Illustration
If index closes at 1300,
A. = (-) 10,500
B. = 2,300
C. = 15,000
D. = 6,800 = 12.17% p.a.

32. Application of Index Futures
In passive Portfolio Management:
An investor willing to invest Rs.1 crore can buy
futures contracts instead of a portfolio, which mimics
the index.
Number of contracts (if Nifty is 5000)
= 1,00,00,000/5000 ×100 = 20 contracts
Advantages:
 Periodic rebalancing will not be required.
 Potential tracking errors can be avoided.
 Transaction costs are less.

33. Application of Index Futures
In Beta Management:
In a bullish market beta should be high and in a
bearish market beta should be low i.e. market timing
and stock selection should be used.
Consider following portfolio and rising market forecast.
Equity : Rs.150 millions
Cash Equivalent : Rs.50 millions
Total : Rs.200 millions
Assume a beta of 0.8 and desired beta of 1.2

34. Application of Index Futures
The Beta can be raised by,
a. Selling low beta stocks and buying high beta stocks
and also maintain 3:1 ratio. Or,
b. Purchasing ‘X’ contracts in the following equation:
150 × 0.8 + 0.02 × X = 200 × 1.2
i.e. X = (200 × 1.2 – 150 × 0.8) / 0.02
= 6000 contracts, assuming
Nifty future available at
Rs.5000, multiple of 4 and
beta of contract as 1.0
No. of contracts will be 600 for a multiple iof 40 and
240 for a multiple is 100.

36. Euro-rate Differentials (Diffs)
Introduced on July 6, 1989 in US, it is a
futures contract tied to differential between
a 3-month non-dollar interest rate and
USD 3-month LIBOR and are cash settled.

37. Euro-rate Differentials (Diffs)
Example: If USD 3-month LIBOR is 7.45 and
Euro 3-month LIBOR is 5.40 at the settlement
time, the diff would be priced at 100 – (7.45 –5.40)
= 97.95. Suppose in January, the March
Euro/dollar diff is prices at 97.60, this would
suggest that markets expects the differential
between USD LIBOR and Euro LIBOR to be
2.40% at settlement in March.

38. Euro-rate Differentials (Diffs)
They are used for:
1. Locking in or unlocking interest rate differentials when
funding in one currency and investing in another.
2. Hedging exposures associated with non-dollar interest-
rate sensitivities.
3. Managing the residual risks associated with running a
currency swap book.
4. Managing risks associated with ever changing interest-
rate differentials for a currency dealer

39. Foreign Exchange Agreements
(FXAs)
They allow the parties to hedge movements
in exchange rate differentials without
entering a conventional currency swap. At
the termination of the agreement, a single
payment is made by one counterparty to
another based on the direction and the
extent of movement in exchange rate differentials.