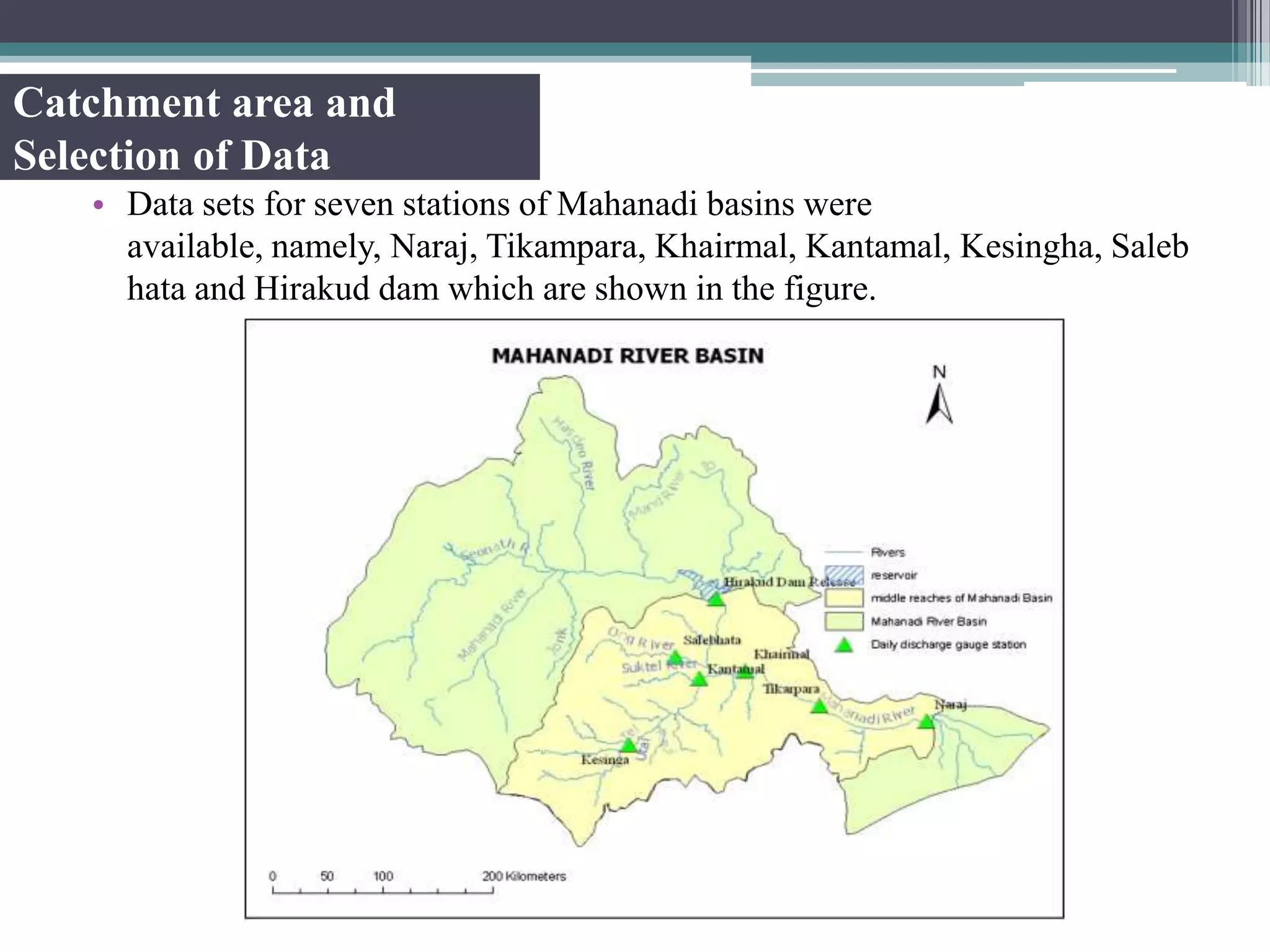
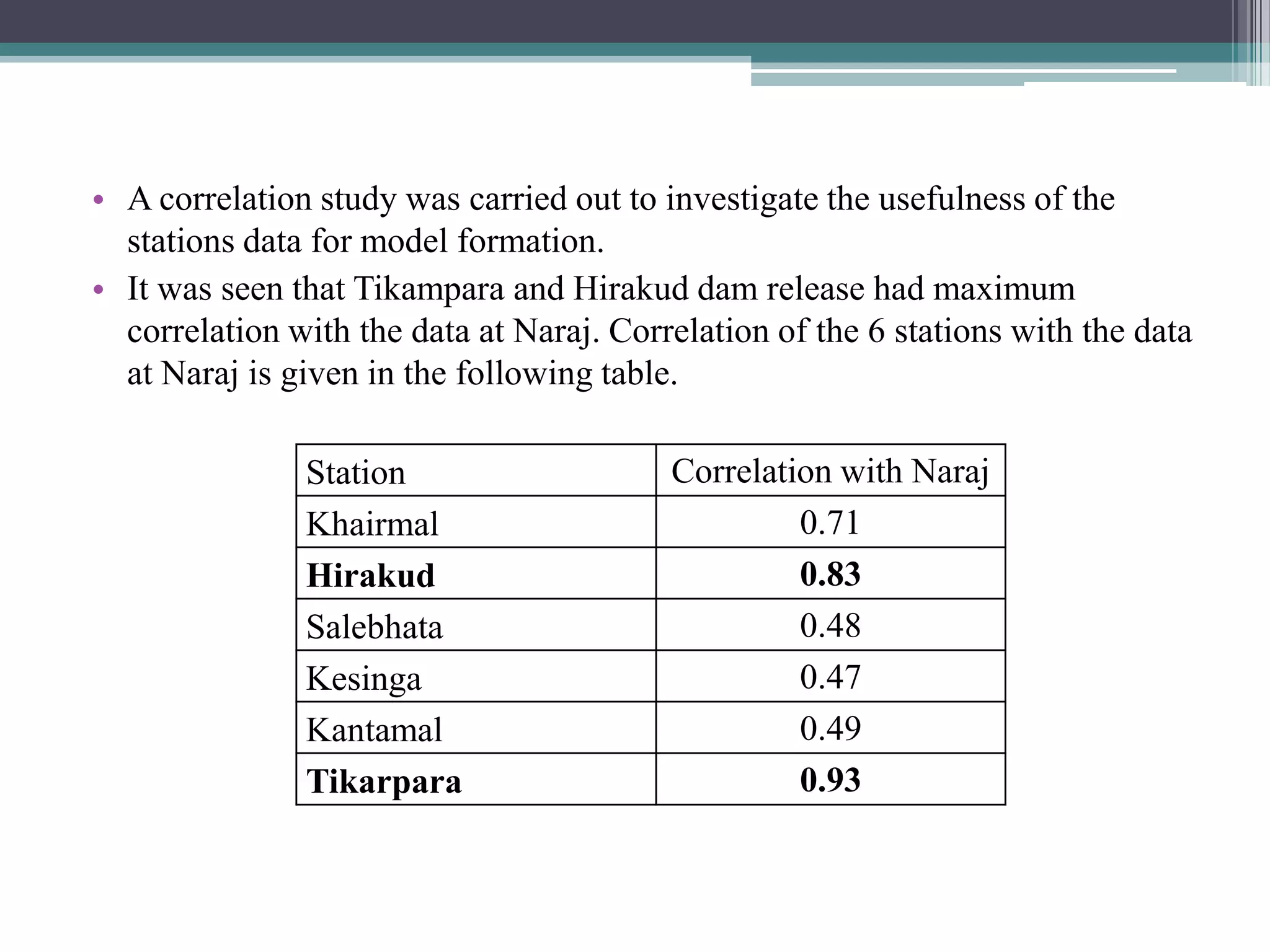
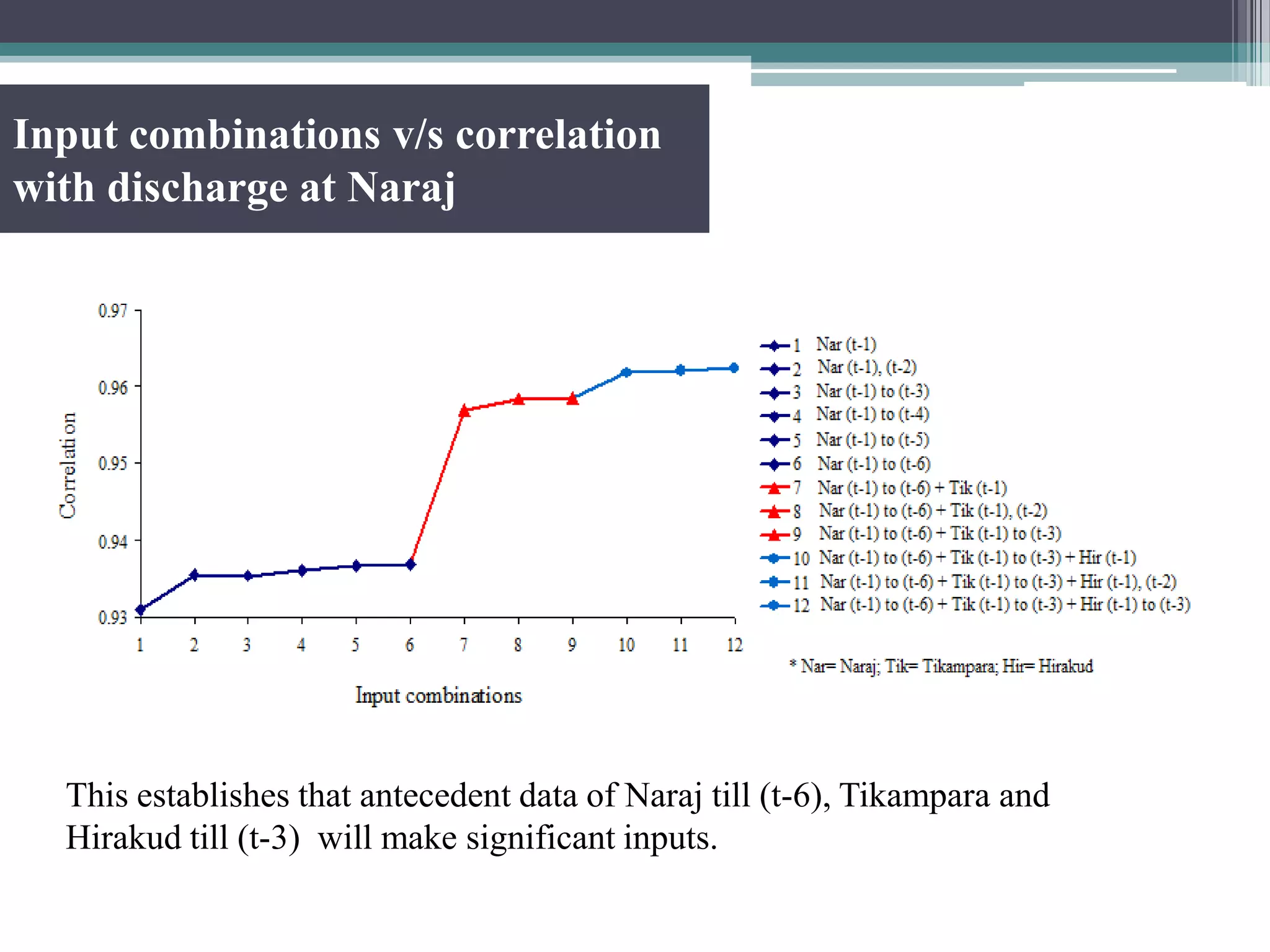
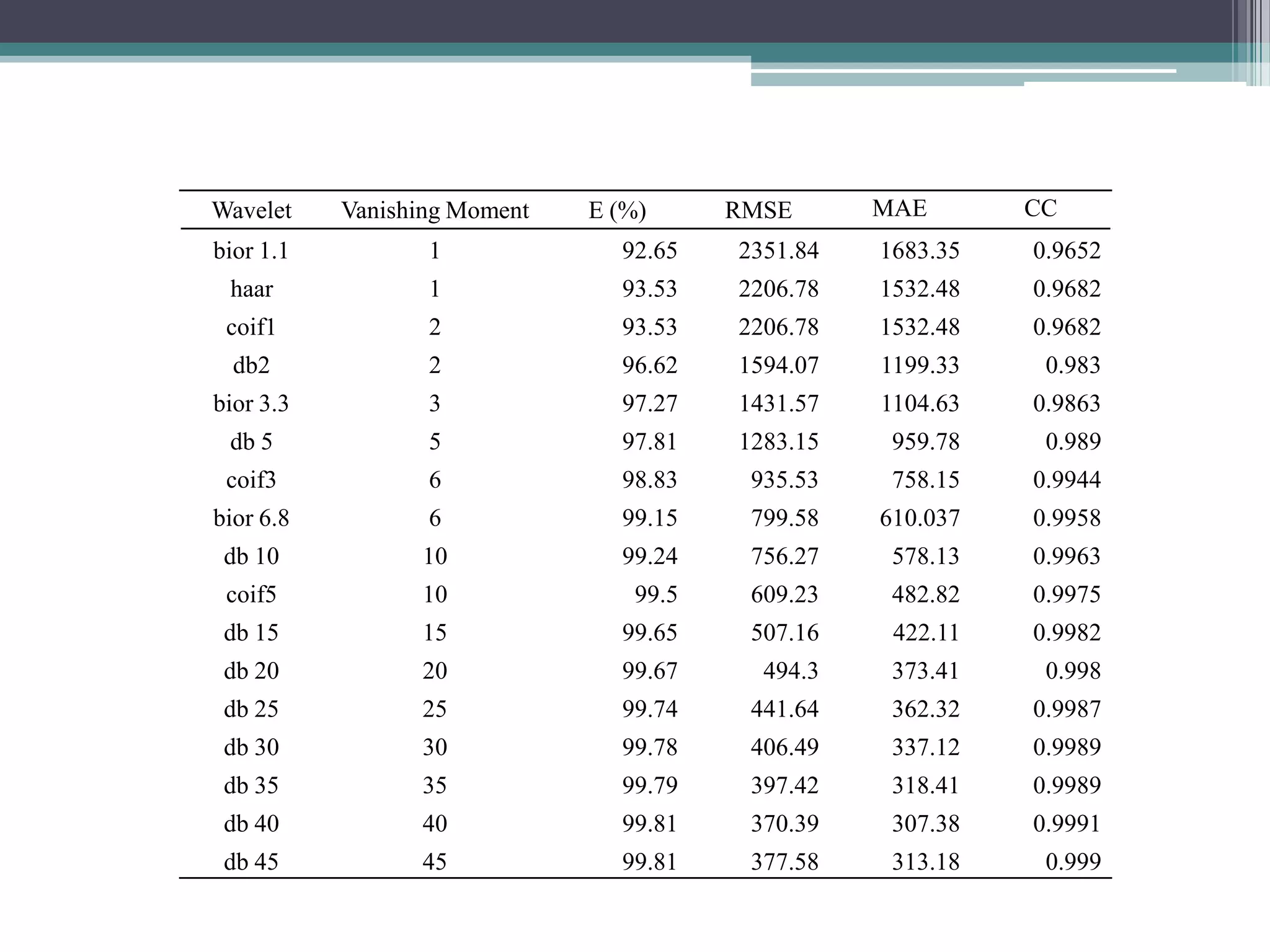
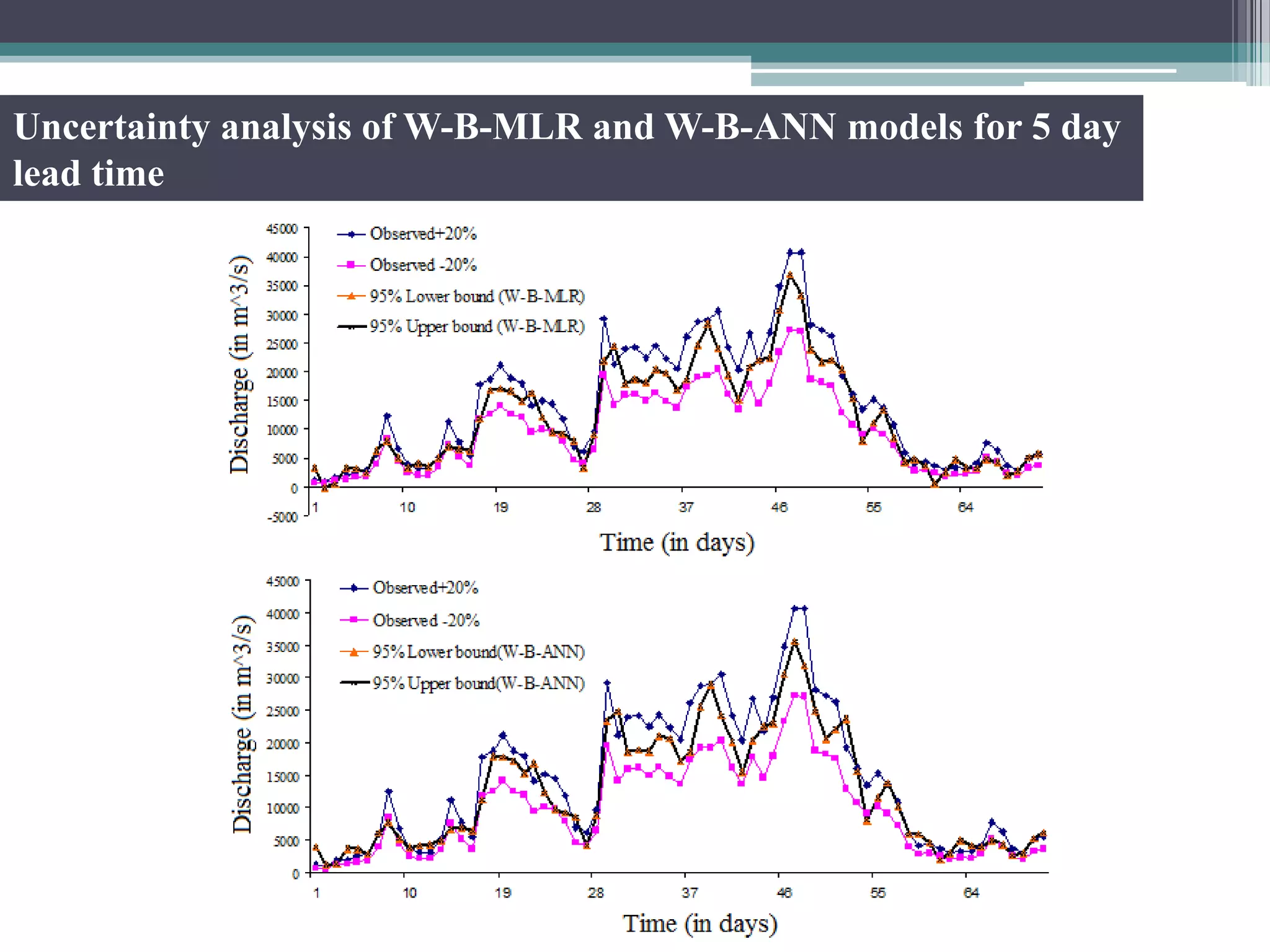
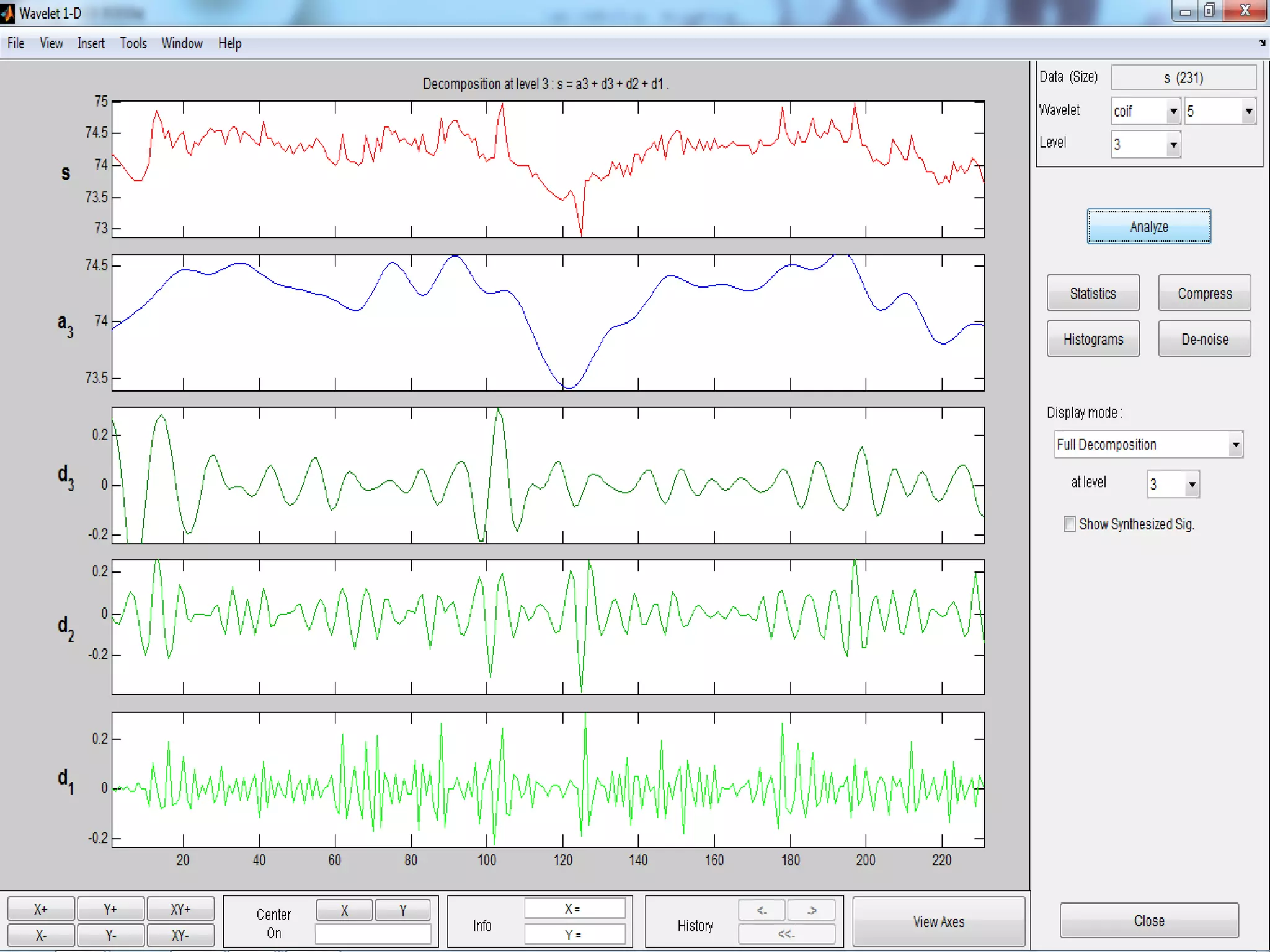
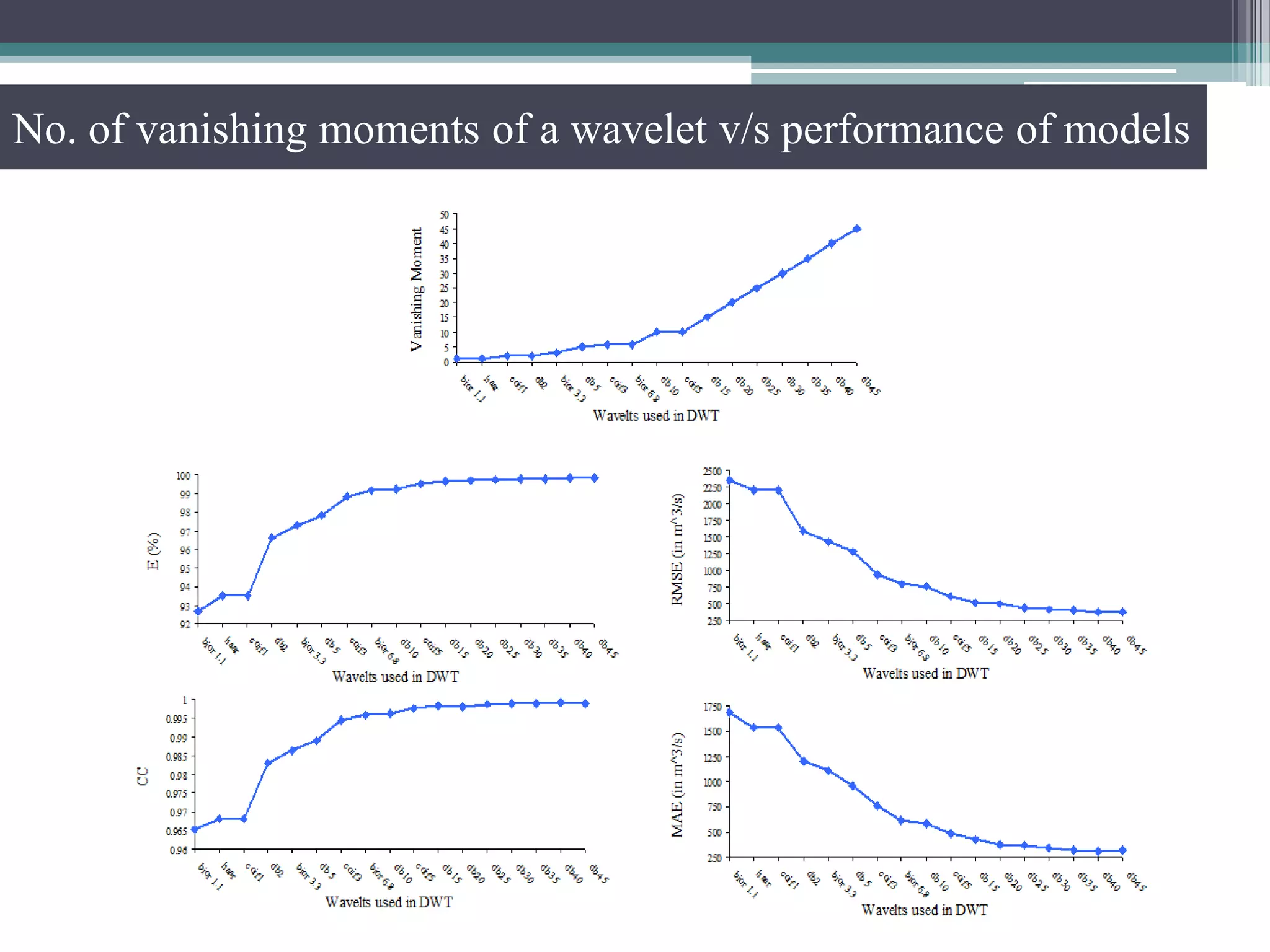
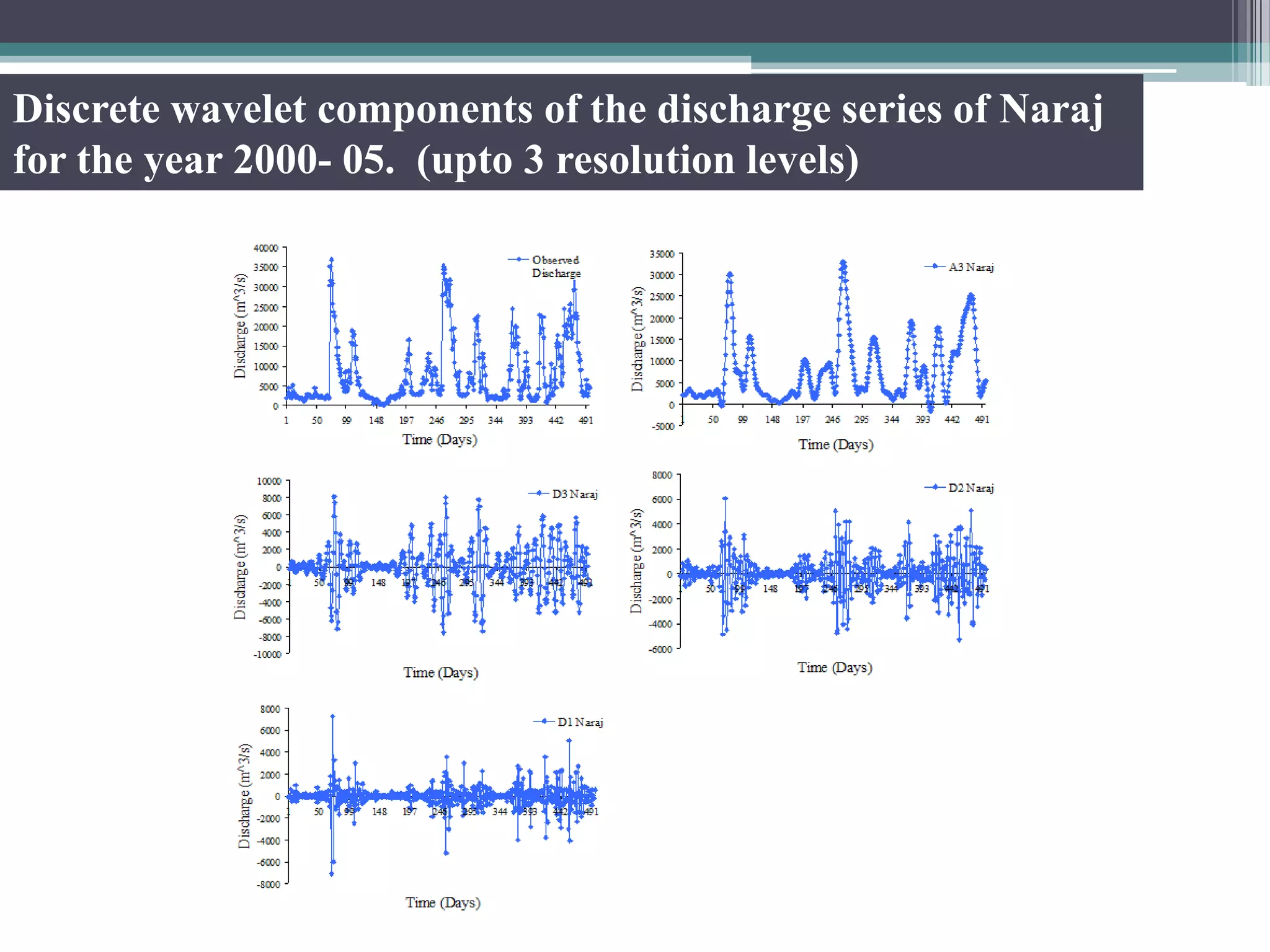
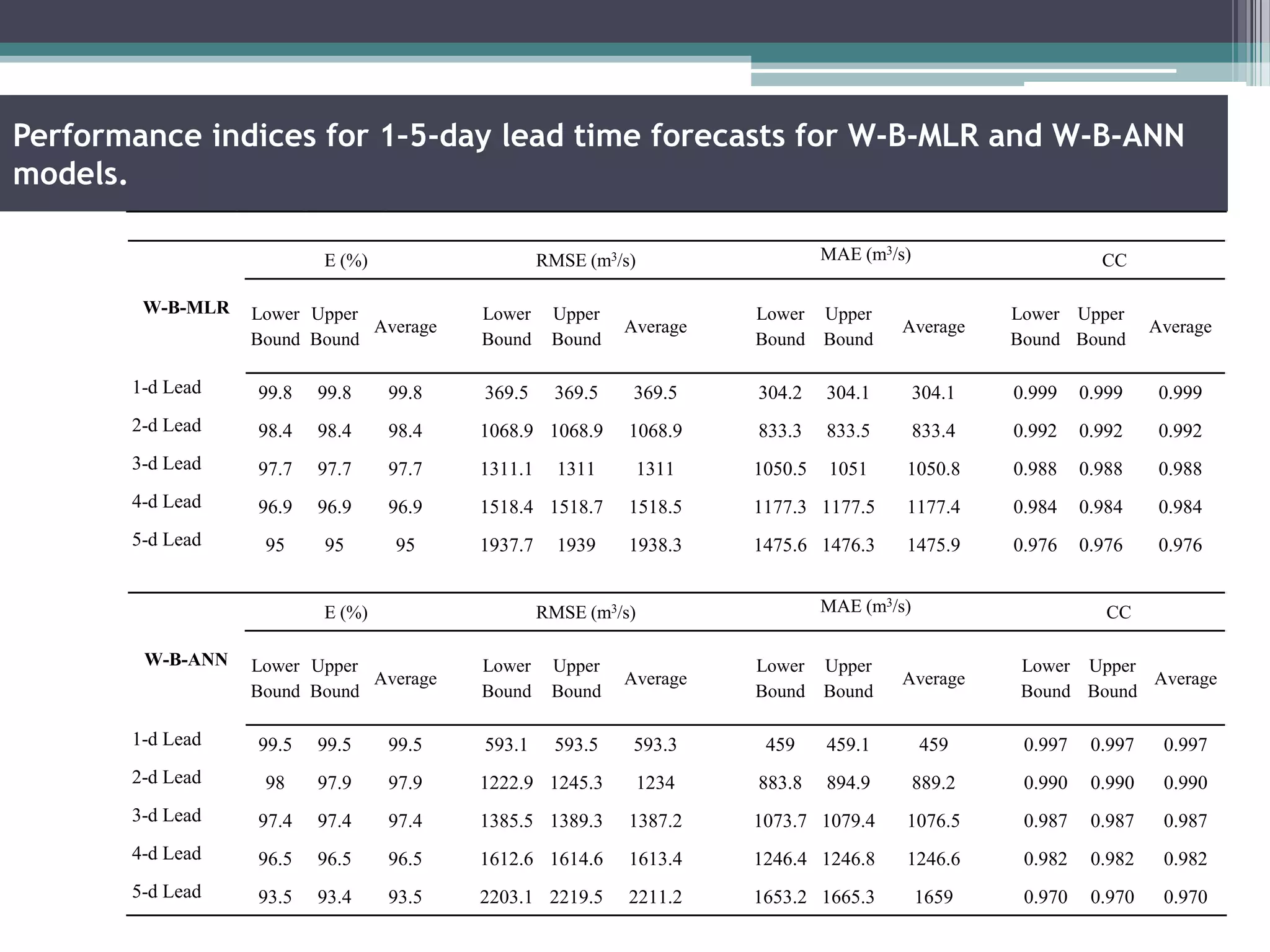
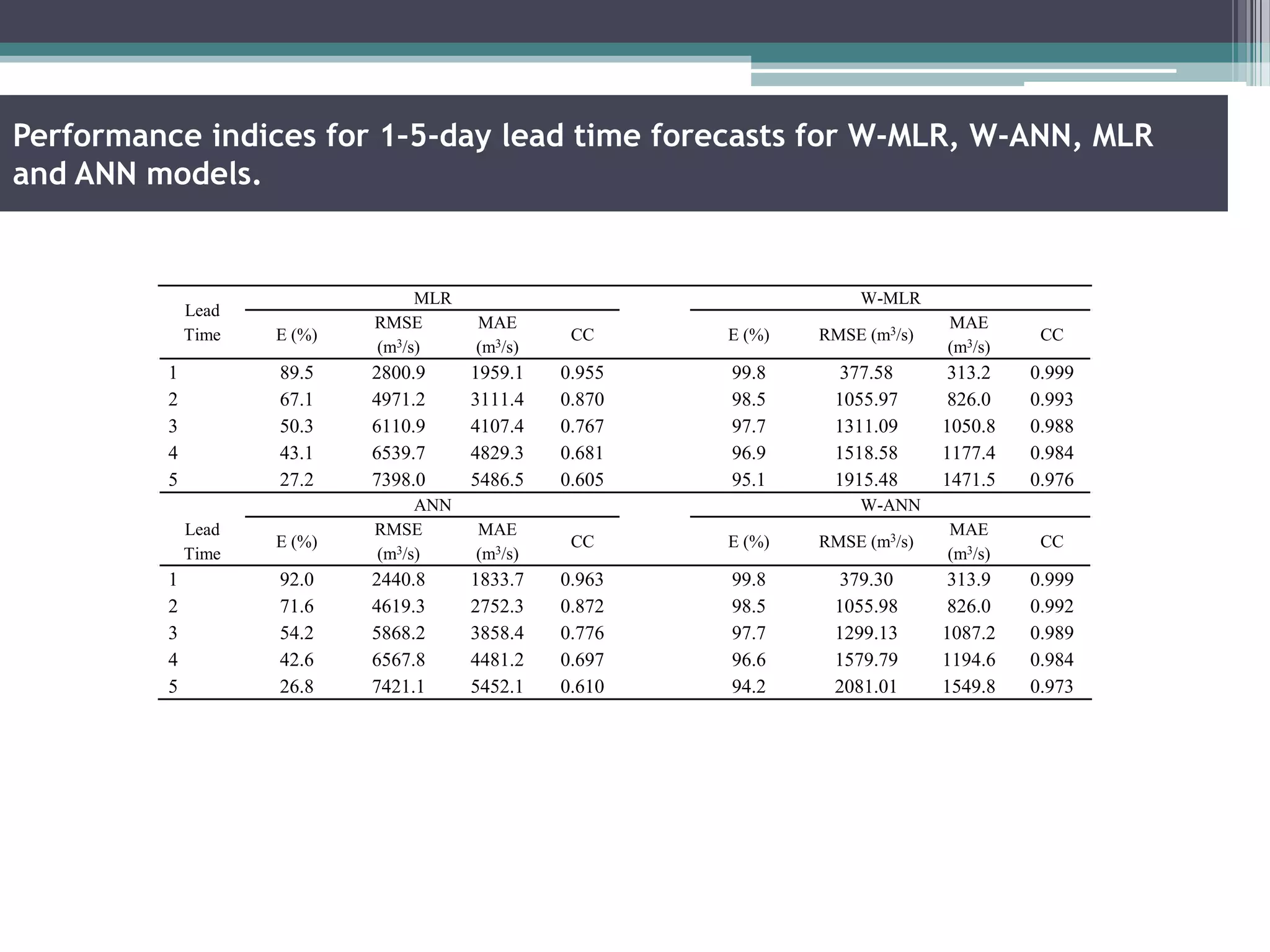
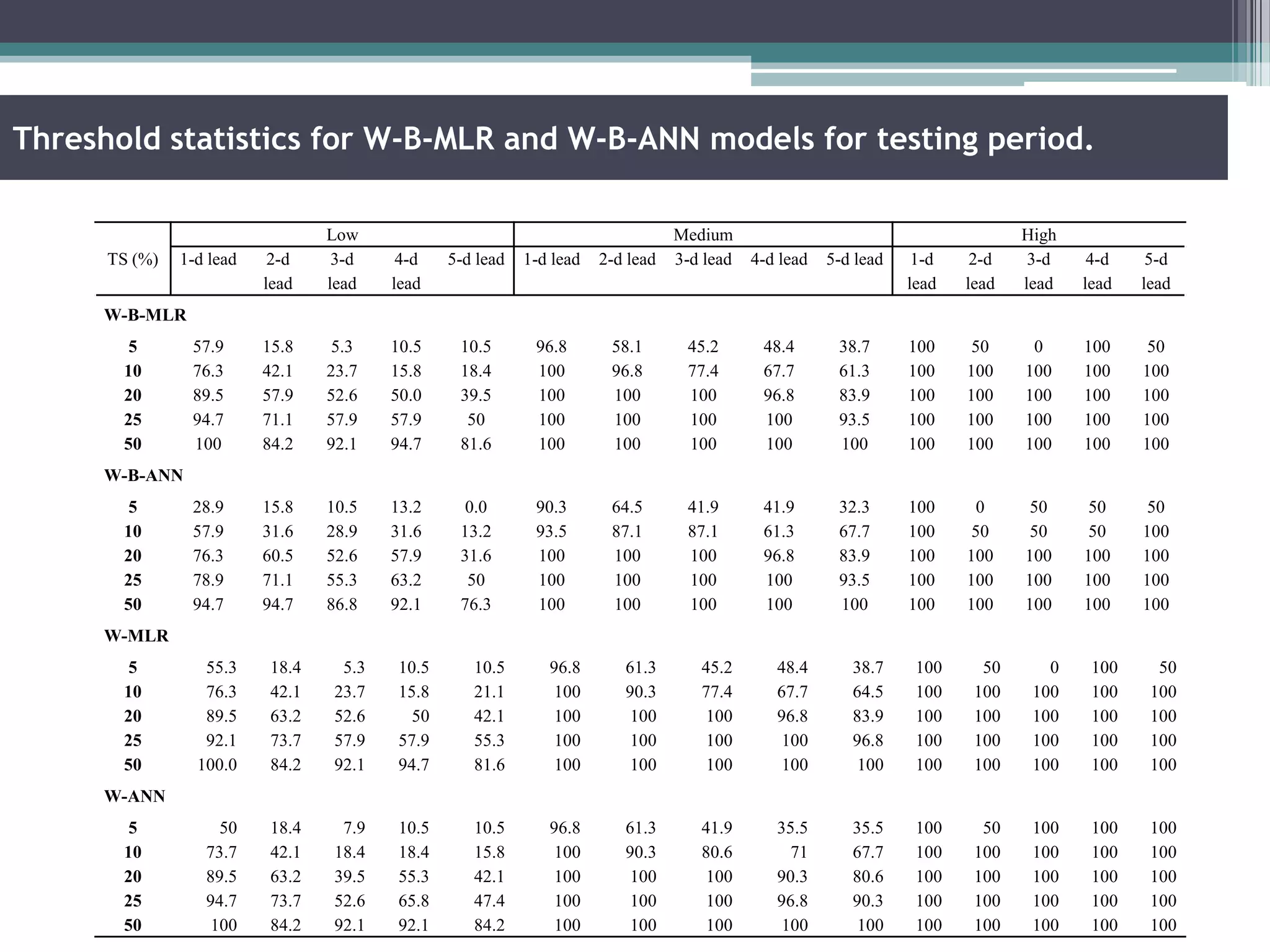
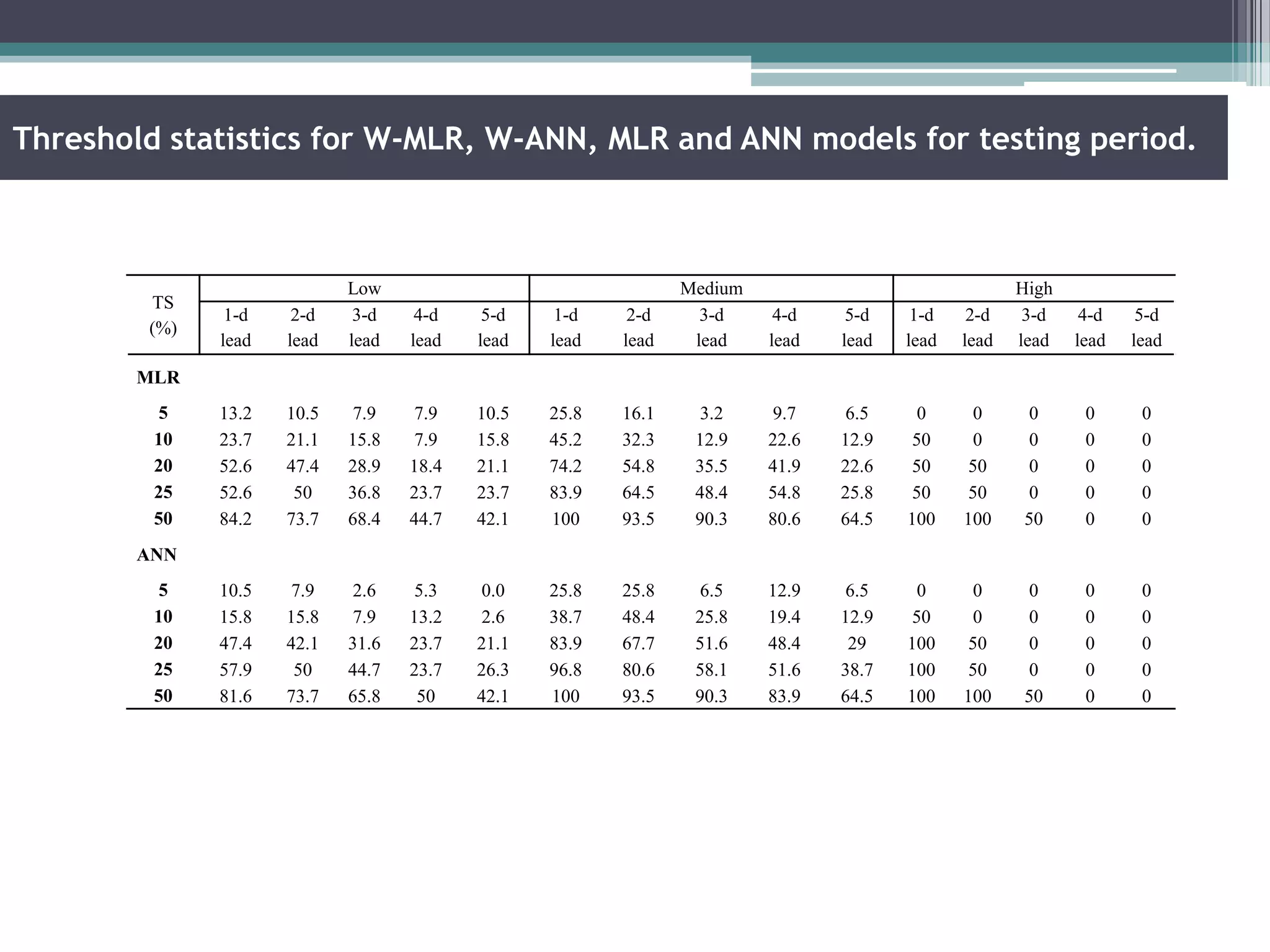
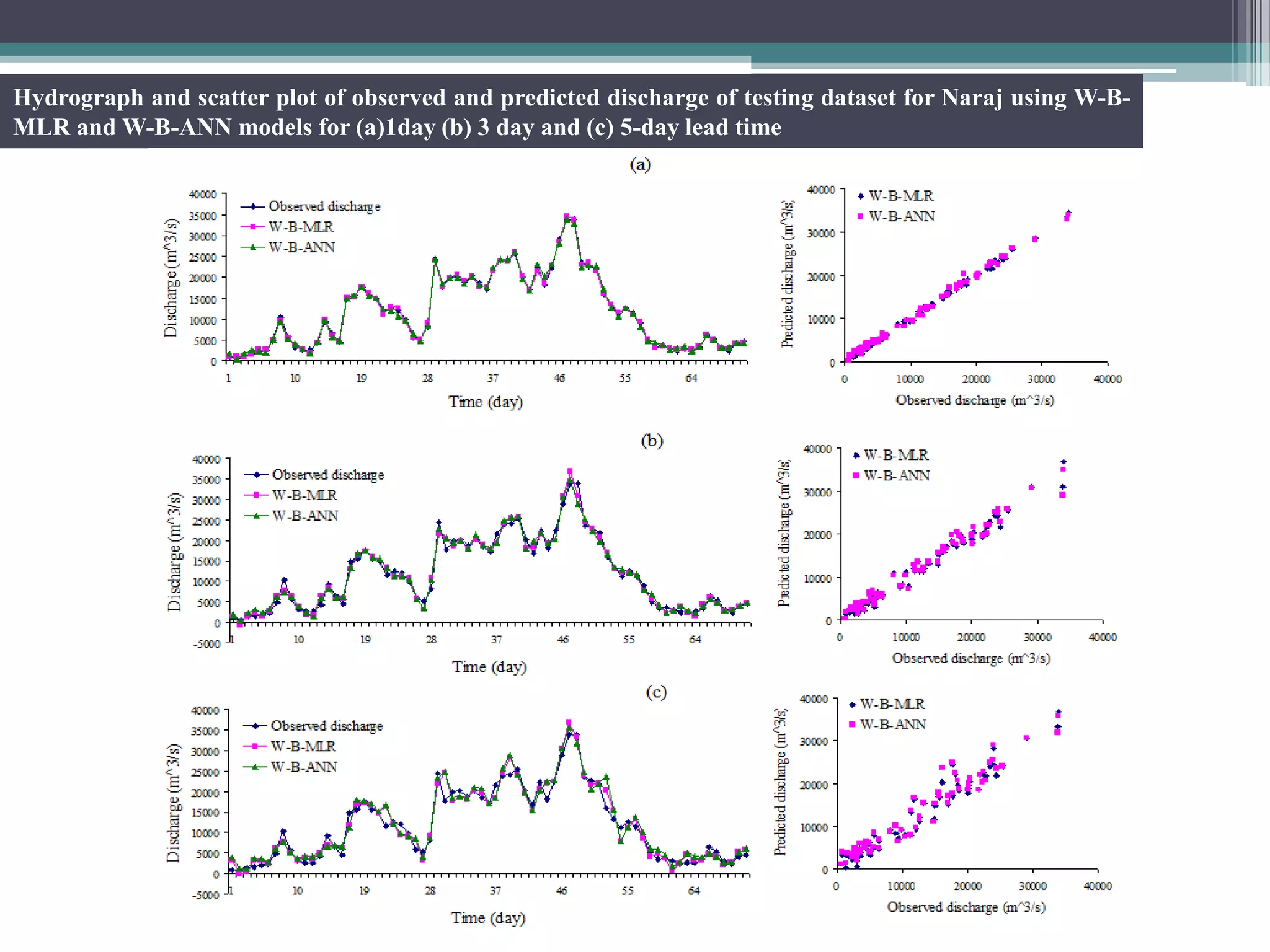
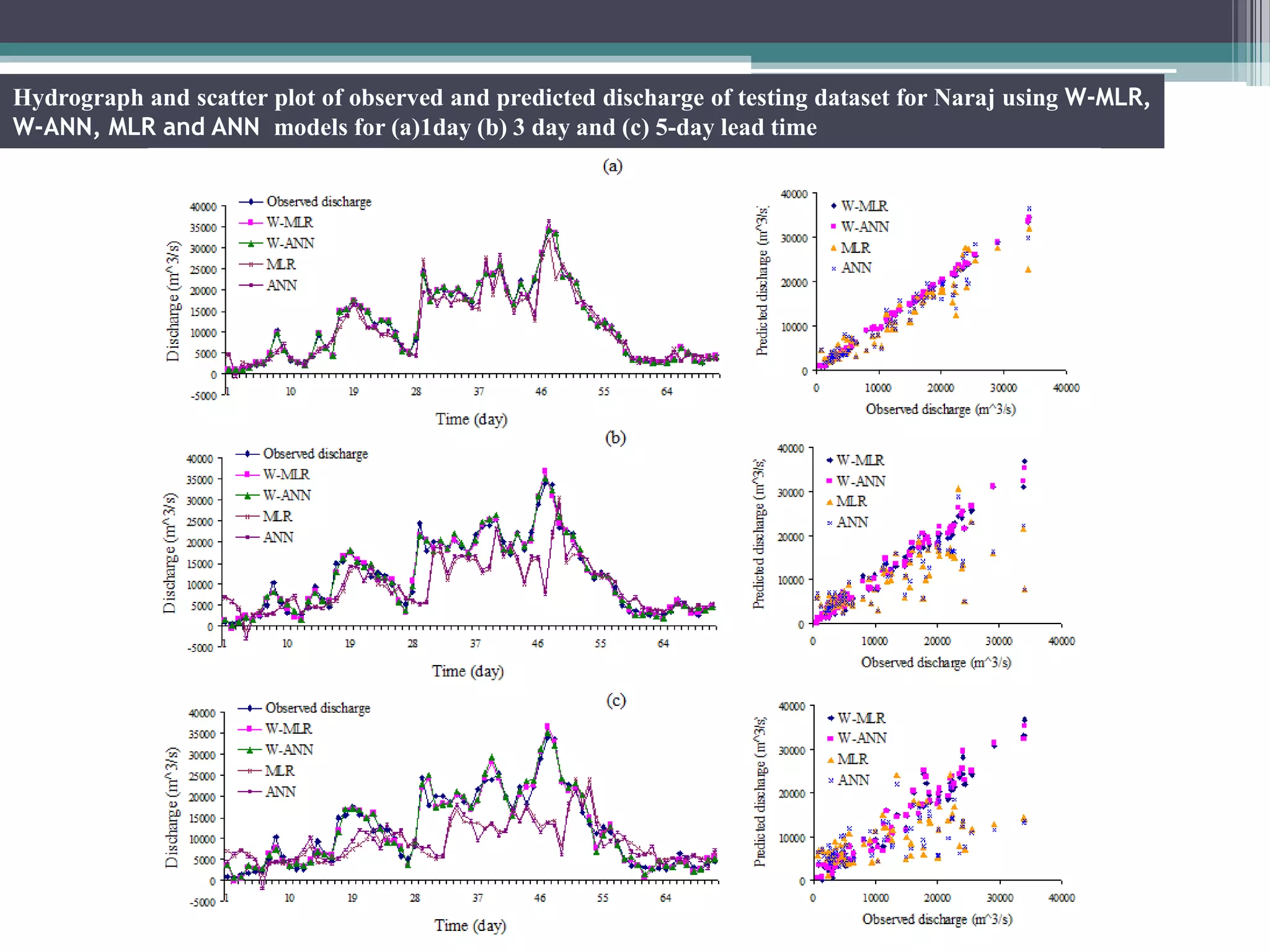
This document summarizes a study that developed and compared multiple linear regression models using wavelet transforms and bootstrap techniques for flood forecasting in the Mahanadi river basin in India. Key aspects of the study included: (1) Selecting significant input variables and wavelets for model development based on correlation analysis, (2) Developing wavelet-bootstrap and wavelet models and comparing their performance to traditional models over lead times of 1-5 days, (3) Finding that wavelet-bootstrap models using the db45 wavelet and incorporating antecedent data outperformed other models with errors below 5% and RMSE below 400 m3/s for 1-day forecasts.

1. Wavelet - Bootstrap based Multiple
linear regression models for flood
forecasting in Mahanadi basin.
- Vinit Sehgal Under The guidance of:
4th year UG Student Dr. C. Chatterjee
Department Of Civil Engineering Agril. & Food Engg. Department
Birla Institute of Technology Indian Institute of Technology
Mesra, Ranchi Kharagpur

2. Problem statement
• The aim of the study was to
(a) develop accurate and reliable models for daily discharge forecasting
based on Wavelet and bootstrap soft computing techniques using the
minimum possible data and
(b) to compare the results with the previous studies on the Mahanadi basin.

3. I

4. Catchment area and
Selection of Data
• Data sets for seven stations of Mahanadi basins were
available, namely, Naraj, Tikampara, Khairmal, Kantamal, Kesingha, Saleb
hata and Hirakud dam which are shown in the figure.

5. • A correlation study was carried out to investigate the usefulness of the
stations data for model formation.
• It was seen that Tikampara and Hirakud dam release had maximum
correlation with the data at Naraj. Correlation of the 6 stations with the data
at Naraj is given in the following table.
Station Correlation with Naraj
Khairmal 0.71
Hirakud 0.83
Salebhata 0.48
Kesinga 0.47
Kantamal 0.49
Tikarpara 0.93

6. • Only discharge at Tikampara and Hirakud release were found to be in good
correlation with the discharge at Naraj.
• Further correlation analysis showed that keeping other stations in the
model formation wont help improve the results (results not shown).
• The correlation study was extended further to decide the significant
antecedent time series from each station in the formation of models.

7. Input combinations v/s correlation
with discharge at Naraj
This establishes that antecedent data of Naraj till (t-6), Tikampara and
Hirakud till (t-3) will make significant inputs.

8. II

9. Selection of Wavelet for DWT
• Selection of wavelets if an important factor on which the performance of
wavelet based models depend.
• Wavelets with high vanishing moments are believed to be more sensitive
towards high frequencies, and hence, are more suitable for application in
hydrological forecasting problems.
• A novel study was carried out in which wavelet based simple MLR models
were formed using 17 wavelets of various families to forecast 1- day ahead
discharge at Naraj using the DWC’s of the significant inputs as described
in slide 6 and the results were tabulated as follows.

10. Wavelet Vanishing Moment E (%) RMSE MAE CC
bior 1.1 1 92.65 2351.84 1683.35 0.9652
haar 1 93.53 2206.78 1532.48 0.9682
coif1 2 93.53 2206.78 1532.48 0.9682
db2 2 96.62 1594.07 1199.33 0.983
bior 3.3 3 97.27 1431.57 1104.63 0.9863
db 5 5 97.81 1283.15 959.78 0.989
coif3 6 98.83 935.53 758.15 0.9944
bior 6.8 6 99.15 799.58 610.037 0.9958
db 10 10 99.24 756.27 578.13 0.9963
coif5 10 99.5 609.23 482.82 0.9975
db 15 15 99.65 507.16 422.11 0.9982
db 20 20 99.67 494.3 373.41 0.998
db 25 25 99.74 441.64 362.32 0.9987
db 30 30 99.78 406.49 337.12 0.9989
db 35 35 99.79 397.42 318.41 0.9989
db 40 40 99.81 370.39 307.38 0.9991
db 45 45 99.81 377.58 313.18 0.999

11. No. of vanishing moments of a wavelet v/s performance of models

12. Conclusion on selection of wavelet for DWT
• It was served that the wavelets from db family performed better than other
family wavelets as they have maximum vanishing moments for a given
support width of a wavelet.
• Greater the vanishing moment of the wavelet used for DWT, better is the
performance of wavelet based models.
• Hence db 45 was considered to be the best wavelet for the model
formation.

13. Discrete wavelet components of the discharge series of Naraj
for the year 2000- 05. (upto 3 resolution levels)

14. III

15. Wavelet- Bootstrap Model formation and performance analysis
• After the significant inputs were decomposed upto 3 levels using db 45
wavelet, these DWC’s were used in the formation of models instead of the
original time series.
• The study compares 6 models namely:
(1) Wavelet- Bootstrap –Multi Linear Regression models (W-B-MLR)
(2) Wavelet- Bootstrap –Neural network models (W-B-ANN)
(3) Wavelet- Multi Linear Regression models (W-MLR)
(4) Wavelet-Neural network models (W-ANN)
(5) Multi Linear Regression models (MLR)
(6) Neural network models (ANN)

16. Performance indices for 1–5-day lead time forecasts for W-B-MLR and W-B-ANN
models.
W-B-MLR
E (%) RMSE (m3/s) MAE (m3/s) CC
Lower
Bound
Upper
Bound
Average
Lower
Bound
Upper
Bound
Average
Lower
Bound
Upper
Bound
Average
Lower
Bound
Upper
Bound
Average
1-d Lead 99.8 99.8 99.8 369.5 369.5 369.5 304.2 304.1 304.1 0.999 0.999 0.999
2-d Lead 98.4 98.4 98.4 1068.9 1068.9 1068.9 833.3 833.5 833.4 0.992 0.992 0.992
3-d Lead 97.7 97.7 97.7 1311.1 1311 1311 1050.5 1051 1050.8 0.988 0.988 0.988
4-d Lead 96.9 96.9 96.9 1518.4 1518.7 1518.5 1177.3 1177.5 1177.4 0.984 0.984 0.984
5-d Lead 95 95 95 1937.7 1939 1938.3 1475.6 1476.3 1475.9 0.976 0.976 0.976
W-B-ANN
E (%) RMSE (m3/s) MAE (m3/s) CC
Lower
Bound
Upper
Bound
Average
Lower
Bound
Upper
Bound
Average
Lower
Bound
Upper
Bound
Average
Lower
Bound
Upper
Bound
Average
1-d Lead 99.5 99.5 99.5 593.1 593.5 593.3 459 459.1 459 0.997 0.997 0.997
2-d Lead 98 97.9 97.9 1222.9 1245.3 1234 883.8 894.9 889.2 0.990 0.990 0.990
3-d Lead 97.4 97.4 97.4 1385.5 1389.3 1387.2 1073.7 1079.4 1076.5 0.987 0.987 0.987
4-d Lead 96.5 96.5 96.5 1612.6 1614.6 1613.4 1246.4 1246.8 1246.6 0.982 0.982 0.982
5-d Lead 93.5 93.4 93.5 2203.1 2219.5 2211.2 1653.2 1665.3 1659 0.970 0.970 0.970

17. Performance indices for 1–5-day lead time forecasts for W-MLR, W-ANN, MLR
and ANN models.
Lead
Time
MLR W-MLR
E (%)
RMSE
(m3/s)
MAE
(m3/s)
CC E (%) RMSE (m3/s)
MAE
(m3/s)
CC
1 89.5 2800.9 1959.1 0.955 99.8 377.58 313.2 0.999
2 67.1 4971.2 3111.4 0.870 98.5 1055.97 826.0 0.993
3 50.3 6110.9 4107.4 0.767 97.7 1311.09 1050.8 0.988
4 43.1 6539.7 4829.3 0.681 96.9 1518.58 1177.4 0.984
5 27.2 7398.0 5486.5 0.605 95.1 1915.48 1471.5 0.976
Lead
Time
ANN W-ANN
E (%)
RMSE
(m3/s)
MAE
(m3/s)
CC E (%) RMSE (m3/s)
MAE
(m3/s)
CC
1 92.0 2440.8 1833.7 0.963 99.8 379.30 313.9 0.999
2 71.6 4619.3 2752.3 0.872 98.5 1055.98 826.0 0.992
3 54.2 5868.2 3858.4 0.776 97.7 1299.13 1087.2 0.989
4 42.6 6567.8 4481.2 0.697 96.6 1579.79 1194.6 0.984
5 26.8 7421.1 5452.1 0.610 94.2 2081.01 1549.8 0.973

18. Threshold statistics for W-B-MLR and W-B-ANN models for testing period.
TS (%)
Low Medium High
1-d lead 2-d
lead
3-d
lead
4-d
lead
5-d lead 1-d lead 2-d lead 3-d lead 4-d lead 5-d lead 1-d
lead
2-d
lead
3-d
lead
4-d
lead
5-d
lead
W-B-MLR
5 57.9 15.8 5.3 10.5 10.5 96.8 58.1 45.2 48.4 38.7 100 50 0 100 50
10 76.3 42.1 23.7 15.8 18.4 100 96.8 77.4 67.7 61.3 100 100 100 100 100
20 89.5 57.9 52.6 50.0 39.5 100 100 100 96.8 83.9 100 100 100 100 100
25 94.7 71.1 57.9 57.9 50 100 100 100 100 93.5 100 100 100 100 100
50 100 84.2 92.1 94.7 81.6 100 100 100 100 100 100 100 100 100 100
W-B-ANN
5 28.9 15.8 10.5 13.2 0.0 90.3 64.5 41.9 41.9 32.3 100 0 50 50 50
10 57.9 31.6 28.9 31.6 13.2 93.5 87.1 87.1 61.3 67.7 100 50 50 50 100
20 76.3 60.5 52.6 57.9 31.6 100 100 100 96.8 83.9 100 100 100 100 100
25 78.9 71.1 55.3 63.2 50 100 100 100 100 93.5 100 100 100 100 100
50 94.7 94.7 86.8 92.1 76.3 100 100 100 100 100 100 100 100 100 100
W-MLR
5 55.3 18.4 5.3 10.5 10.5 96.8 61.3 45.2 48.4 38.7 100 50 0 100 50
10 76.3 42.1 23.7 15.8 21.1 100 90.3 77.4 67.7 64.5 100 100 100 100 100
20 89.5 63.2 52.6 50 42.1 100 100 100 96.8 83.9 100 100 100 100 100
25 92.1 73.7 57.9 57.9 55.3 100 100 100 100 96.8 100 100 100 100 100
50 100.0 84.2 92.1 94.7 81.6 100 100 100 100 100 100 100 100 100 100
W-ANN
5 50 18.4 7.9 10.5 10.5 96.8 61.3 41.9 35.5 35.5 100 50 100 100 100
10 73.7 42.1 18.4 18.4 15.8 100 90.3 80.6 71 67.7 100 100 100 100 100
20 89.5 63.2 39.5 55.3 42.1 100 100 100 90.3 80.6 100 100 100 100 100
25 94.7 73.7 52.6 65.8 47.4 100 100 100 96.8 90.3 100 100 100 100 100
50 100 84.2 92.1 92.1 84.2 100 100 100 100 100 100 100 100 100 100

19. Threshold statistics for W-MLR, W-ANN, MLR and ANN models for testing period.
TS
(%)
Low Medium High
1-d
lead
2-d
lead
3-d
lead
4-d
lead
5-d
lead
1-d
lead
2-d
lead
3-d
lead
4-d
lead
5-d
lead
1-d
lead
2-d
lead
3-d
lead
4-d
lead
5-d
lead
MLR
5 13.2 10.5 7.9 7.9 10.5 25.8 16.1 3.2 9.7 6.5 0 0 0 0 0
10 23.7 21.1 15.8 7.9 15.8 45.2 32.3 12.9 22.6 12.9 50 0 0 0 0
20 52.6 47.4 28.9 18.4 21.1 74.2 54.8 35.5 41.9 22.6 50 50 0 0 0
25 52.6 50 36.8 23.7 23.7 83.9 64.5 48.4 54.8 25.8 50 50 0 0 0
50 84.2 73.7 68.4 44.7 42.1 100 93.5 90.3 80.6 64.5 100 100 50 0 0
ANN
5 10.5 7.9 2.6 5.3 0.0 25.8 25.8 6.5 12.9 6.5 0 0 0 0 0
10 15.8 15.8 7.9 13.2 2.6 38.7 48.4 25.8 19.4 12.9 50 0 0 0 0
20 47.4 42.1 31.6 23.7 21.1 83.9 67.7 51.6 48.4 29 100 50 0 0 0
25 57.9 50 44.7 23.7 26.3 96.8 80.6 58.1 51.6 38.7 100 50 0 0 0
50 81.6 73.7 65.8 50 42.1 100 93.5 90.3 83.9 64.5 100 100 50 0 0

20. Hydrograph and scatter plot of observed and predicted discharge of testing dataset for Naraj using W-B-
MLR and W-B-ANN models for (a)1day (b) 3 day and (c) 5-day lead time

21. Hydrograph and scatter plot of observed and predicted discharge of testing dataset for Naraj using W-MLR,
W-ANN, MLR and ANN models for (a)1day (b) 3 day and (c) 5-day lead time

22. Uncertainty analysis
• CWC suggests that 20 % (plus or minus) error in forecasting discharge is
acceptable. So the pattern of the 95% upper and lower bands of the
predictions using Bootstrap methods was studied with respect to the 20%
upper and lower band of the original discharge at Naraj.

23. Uncertainty analysis of W-B-MLR and W-B-ANN models for 5 day
lead time