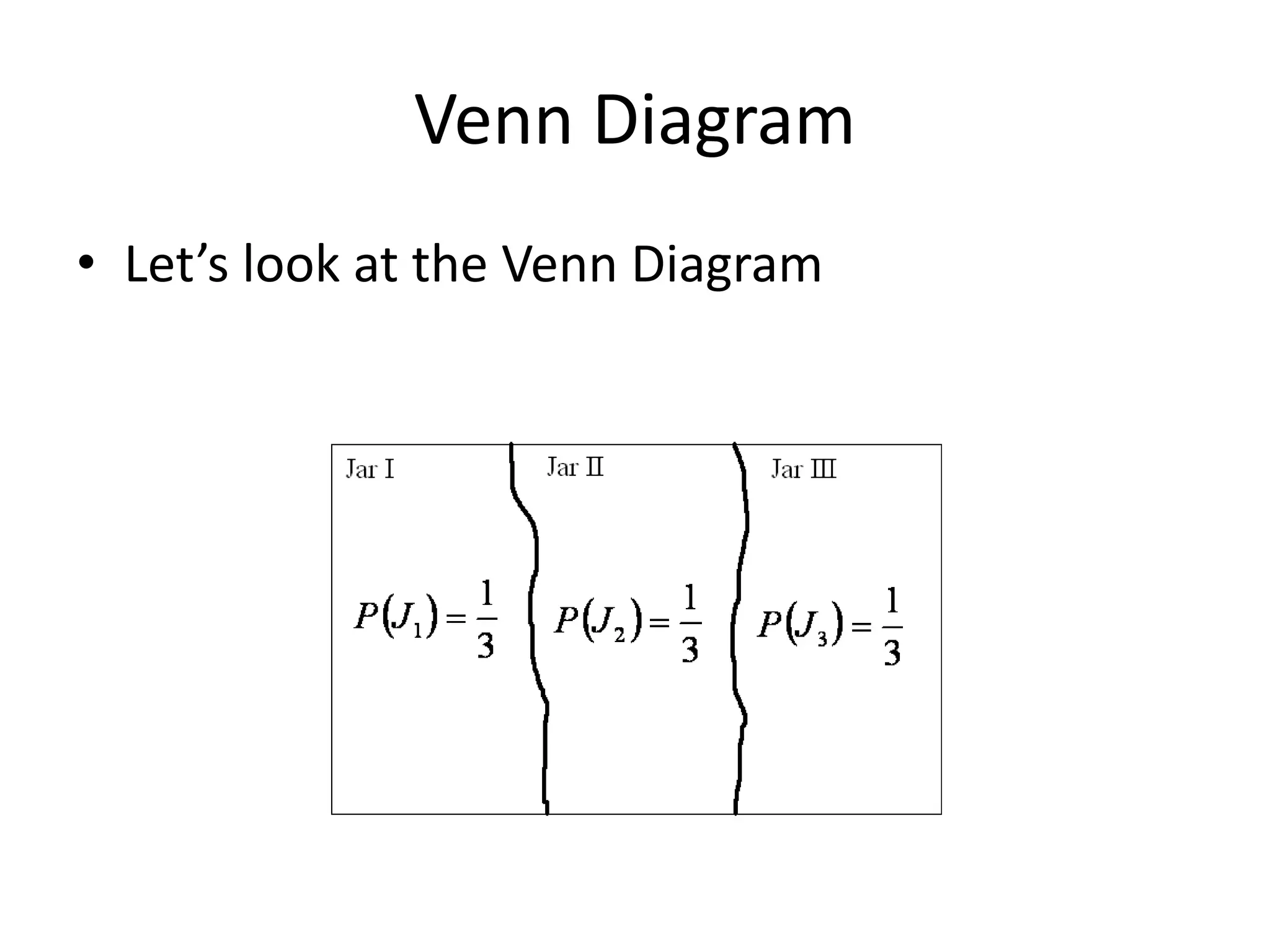
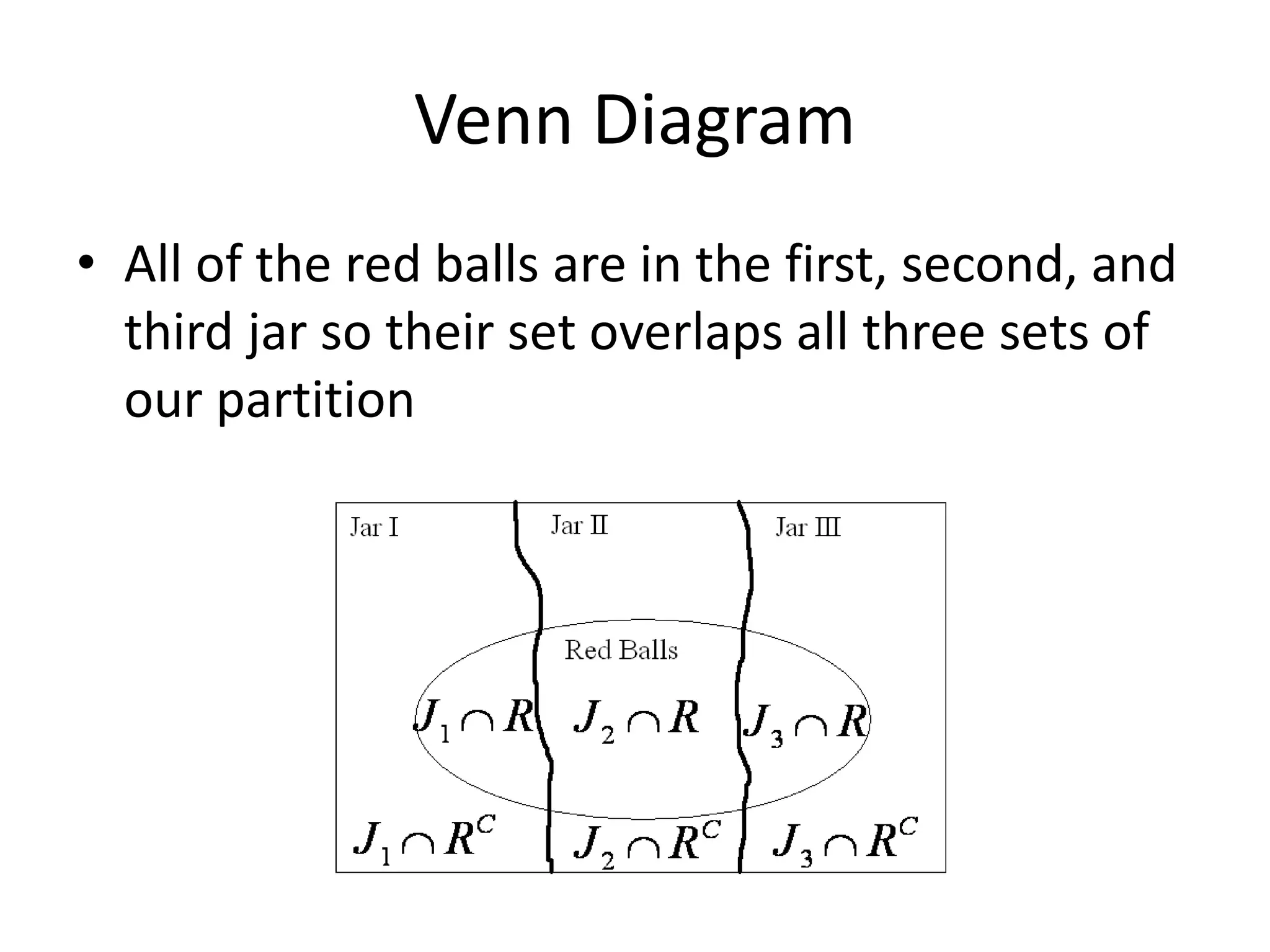
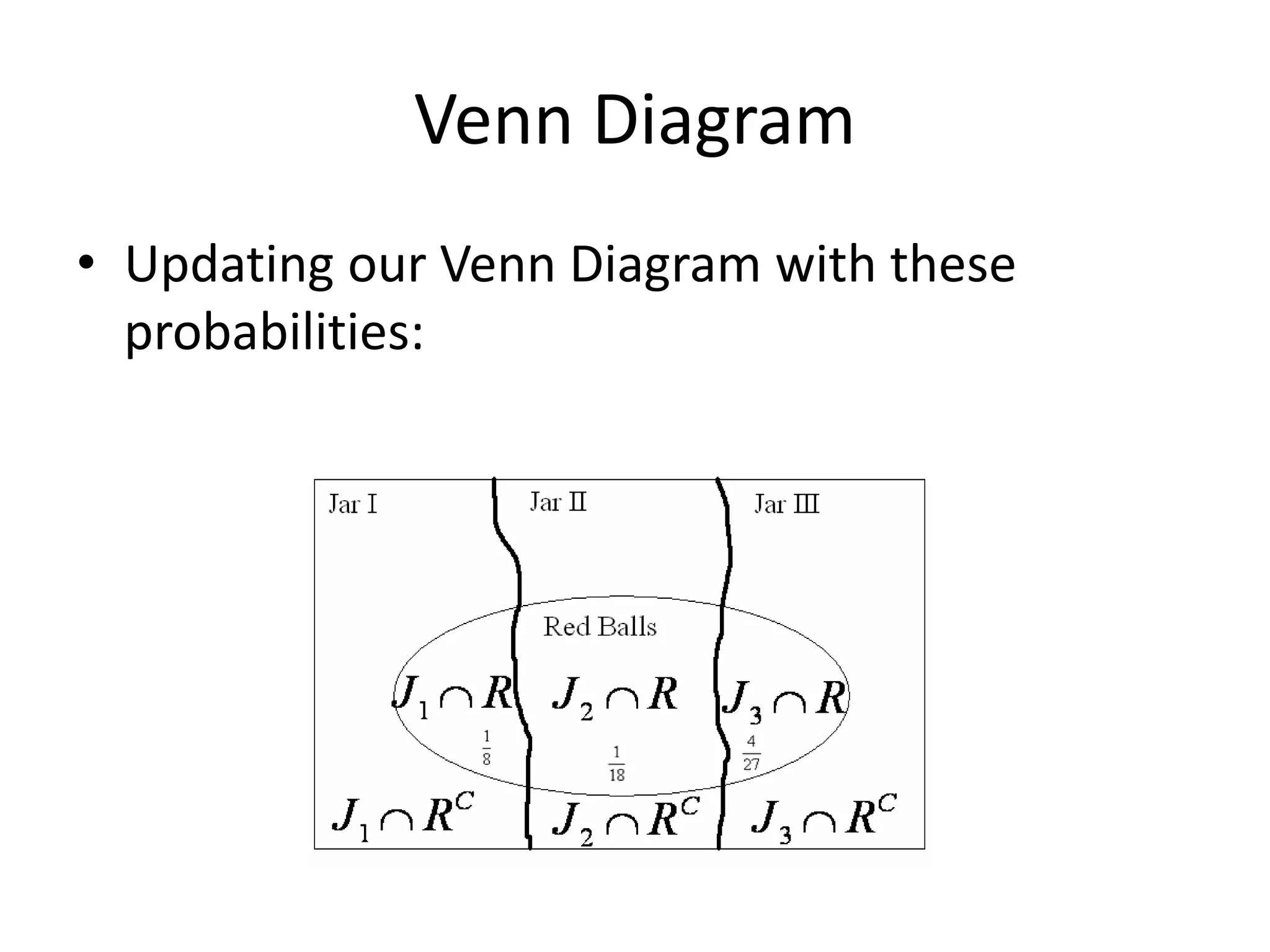
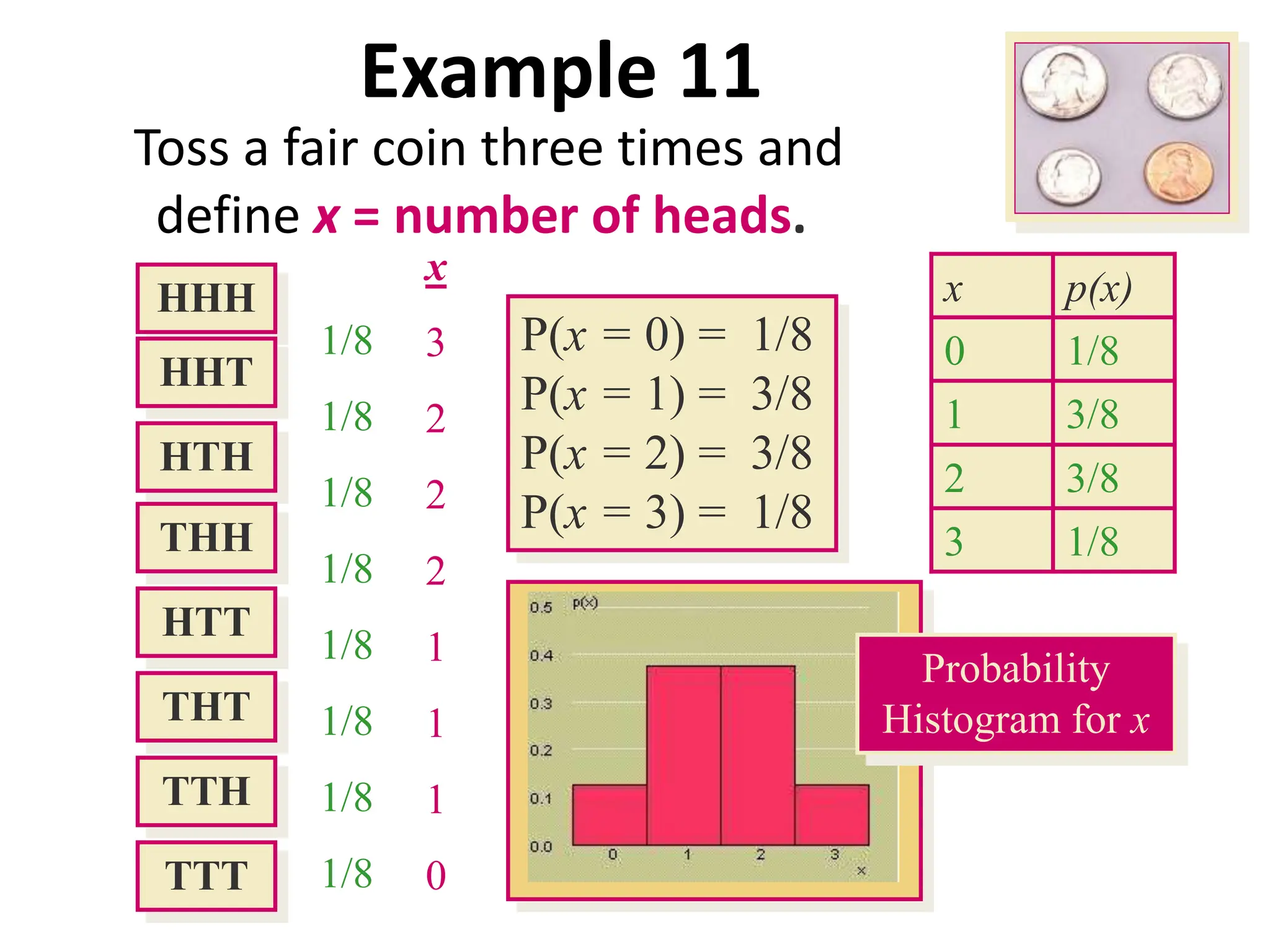
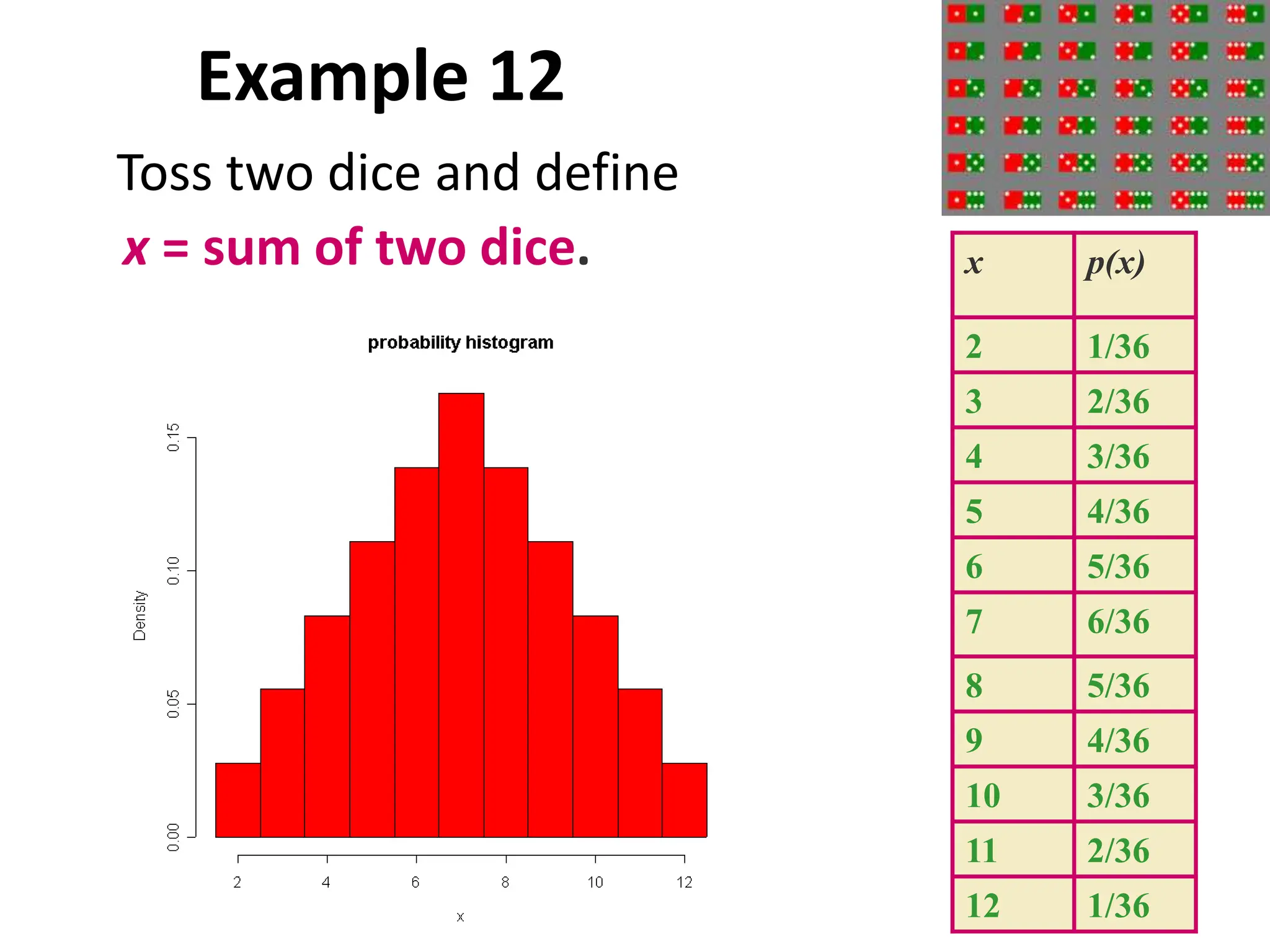
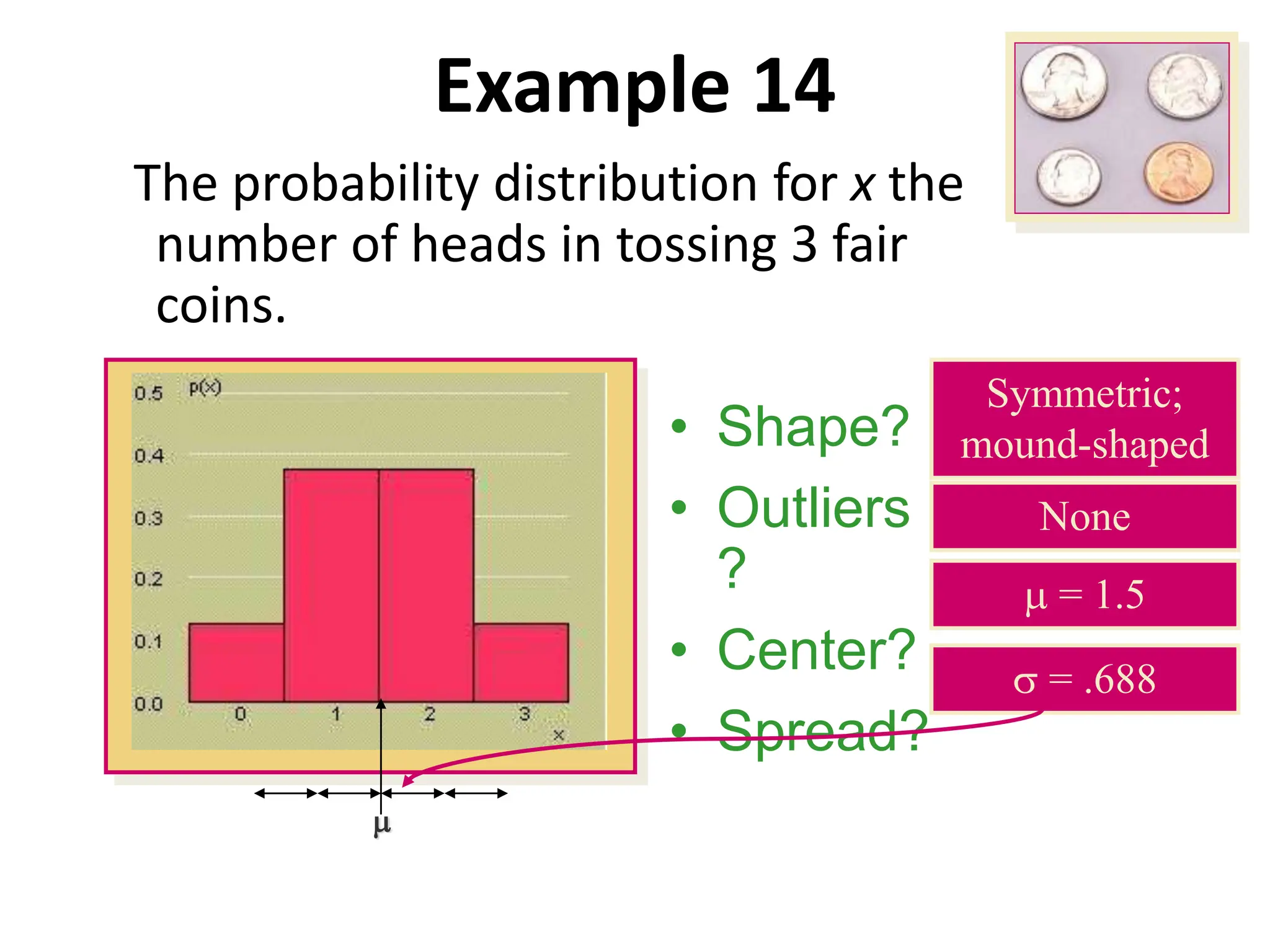
The document provides a summary of topics related to conditional probability, Bayes' theorem, and independent events. It includes examples and formulas for conditional probability, multiplication rule of probability, total probability rule, Bayes' rule, and independent events. It also discusses pairwise and mutually independent events. The document concludes with examples demonstrating applications of conditional probability, Bayes' theorem, multiplication rule, total probability rule, and independent events.









![Example 5
Two coins be tossed, let
A={H in the 2nd throw}
B={ H in the 1st throw}, Are A and B independent events?
Sol:
Ω={HH,HT,TH,TT}
A={HH,TH} P(A)=2/4=1/2
B={HH,HT} P(B)=2/4=1/2
A∩B={HH] p(A∩B)=1/4
P(A|B)=
p(A∩B)
𝑃(𝐵)
=
1/4
1/2
= 1/2 i.e P(A|B)= P(A)
P(A).P(B)=(1/2).(1/2)=1/4
Then : A and B are independent events](https://image.slidesharecdn.com/lecture5conditionalprobabilitybayest-231117072614-ef77cde4/75/Lecture_5Conditional_Probability_Bayes_T-pptx-10-2048.jpg)