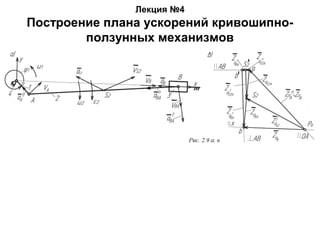
Документ описывает методику построения планов ускорений для кривошипно-ползунных механизмов, включая векторные уравнения для определения линейных и угловых ускорений звеньев механизма. Уделяется внимание нормальным, тангенциальным и кориолисовым ускорениям, а также графико-аналитическим методам для определения скоростей и ускорений центров тяжести. Приведены формулы и методы вычисления различных составляющих ускорений и скоростей звеньев, что позволяет проводить кинематический анализ механизмов с гидроцилиндром.

1. Лекция №4
Построение плана ускорений кривошипноползунных механизмов

2. Векторное уравнение для построения плана ускорений
Построение плана ускорений позволяет определить линейные ускорения точек А, В и S2 ,
а также угловое ускорение звена 2.
n
Ускорение точки А кривошипа складывается из суммы нормальной a A и тангенциальной
t
a A составляющих
n
t
a A = aA + a A,
(2.42)
n
2 t
где a A =  1ω1 ; a A =  1ε1. = 0, если ω1 = const.
Ускорение точки В, принадлежащей звену 2, можно представить в виде векторной суммы
ускорений переносного и относительного движений
(2.43)
a B = a Bе + a Br ,
где a Bе = a A ; a Br = a BA .
Относительное ускорение точки В также состоит из двух составляющих
n
t
a BA = a BA + a BA ,
(2.44)
t
n
2
где aBA =  2ω2 ; a BA =  2ε 2 .
dω1
С учетом приведенных выше формул и в случае = ε1 = 0
окончательно получим
dt
n
n
t
a B = a A + a BA + a BA .
(2.45)
// х // OA // AB ⊥ BA

3. Построение плана ускорений
Построение плана ускорений начинаем с выбора масштабного коэффициента плана
n
n
ускорений K a по любой известной величине – либо по a A , либо по aВA. Пусть
n
aA
(2.46)
Ka = n ,
ZaA
n
n
где Z a A - длина отрезка, изображающего ускорение a A .
n
n
n
n
Z a BA, изображающего известное ускорение aBA , будет Z a BA = a BA .
Тогда величина отрезка
Ka
t
t
aBA = K a ⋅ Z aBA и aB = K a ⋅ Z aB .
Так как вектор ускорения a B направлен в сторону отрицательной полуоси х, то знак
ускорения a B будет отрицательным.
aв
Соединив прямой точки а и b плана ускорений, получим отрезок , изображающий полное
BA
относительное ускорение
. Его aвеличина будет
aBA = K a ⋅ aв.
Величина углового ускорения звена 2 определяется из уравнения
t
aBA
ε2 =
, ε 2 < 0.
(2.47)
2
Ускорение точки S2 определяется из векторного уравнения
n
aS 2 = a A + a S 2 A.
(2.48)
// OA // a BA
Величина относительного ускорения aS 2 A находится аналогично скорости υS2 A - методом
aBA
пропорционального деления отрезка
ab, изображающего относительное ускорение
(2.49)
 AS 2 
 AS 2 
a S 2 A = a BA 
 или на рис. 2.9, в a S 2 = аb
.
AB 
 AB 

Полное ускорение точки
определяется как aS 2 = Z aS 2 ⋅ K a .
S2

4. Графоаналитический метод кинематического анализа
механизма с гидроцилиндром
План положений

План положений механизма для заданного значения обобщенной координаты 21 показан
 AB
ϕ4
на рис. 2.10, а. По известным длинам звеньев ,  3 =  BC ,  4 =  AC
и углу определяются
угловые положения звеньев 1-2 и 3 ϕ1 и ϕ3 На рисунке точка S3 является центром тяжести
.
звена 3, положение которого определяется углом α и длиной  CS3 , а точки Sц и Sn - центры
тяжести соответственно цилиндра и поршня со штоком. План положений построен в
соответствии с масштабным коэффициентом K  , определенным по длине какого-либо звена
механизма.

5. План механизма с гидроцилиндром
План скоростей позволит определить угловые скорости звеньев 1-2 и 3, линейные скорости центров
тяжести всех звеньев по заданным кинематической схеме механизма, построенной в масштабе (рис. 2.10,
а) и закону движения начального звена, например υ21 = const.
Абсолютная скорость υB 2
точки, принадлежащей звену 2, равна геометрической сумме переносной
υBе и относительной υBr скоростей этой точкиυB 2 = υ Bе + υBr .
(2.50)
При определении переносной скорости точки предполагается, что относительное движение точки
остановлено. Переносной скоростью точки В звена 2 является движение со скоростью точки В,
принадлежащей звену 1 υB1, а относительной скоростью является поступательное движение звена 2
относительно звена 1, т.е. υ Bе = υ B1 и υBr = υ21.
υ B3 = υ B1 + υ 21.
С учетом равенства υB2 = υB3 векторное уравнение скоростей будет иметь вид ⊥ BC ⊥ AB // AB (2.51)
Данное векторное уравнение решается, поскольку оно имеет не более двух неизвестных –
определению подлежат модули абсолютных скоростей точек B1 и B3 υ B1 и υ B3 .
Масштабный коэффициент плана скоростей K υ =
υ21
.
Zυ21
B
Неизвестные скорости определяются как υB1 = K υ ⋅ Zυ B1 ; υυ3 = K υ ⋅ ZυB3 .
υ B1
; ω3 = B 3 , ω1 < 0, ω3 > 0
ω1 и ω3 равны ω1 =
Угловые скорости звеньев
 AB
3
(2.53)

6. Линейные скорости центров тяжести звеньев
Линейная скорость центра тяжести цилиндра Sц (звено 1) как точки, лежащей на звене АВ,
находится методом пропорционального деления отрезка p υв1, изображающего скорость υB1:
 AS 
ZυSц = ZυB1  ц 
 AB  .
Sn
Линейная скорость центра тяжести поршня (звено 2), совершающего сложное движение,
определяется, как и для точки , суммированием переносной и относительной скоростей
υSn = υSne + υSnr
или
υSn = υSn1 + υ 21 ,
(2.54)
⊥ АВ ⊥ АВ
где υSn1 - вектор скорости точки, принадлежащей цилиндру и лежащей на расстоянии
 ASn от точки А, определяется аналогично скорости точки центра тяжести цилиндра S ц .
Численные значения скоростей равны
υSц = Кυ ⋅ ZυSц ; υSn = Кυ ⋅ ZυSn .
Вектор линейной скорости центра тяжести третьего звена S3 направлен перпендикулярно
линии CS3 в соответствии со знаком угловой скорости . ω3
Величина скорости определяется как
υS3 = lcs 3 ⋅ ω3
.

7. Векторное уравнение для построения плана
ускорения механизма с гидроцилиндром.
План ускорений механизма с гидроцилиндром позволяет определить угловые ускорения звеньев 1-2 и
3, а также линейные ускорения центров тяжести всех звеньев.
При составлении уравнения ускорений следует учитывать, что абсолютное ускорение a B 2 точки В,
принадлежащей второму звену, складывается из геометрической суммы трех ускорений – переносного
вместе с первым звеном a Bе , относительного a Br и кориолисова ускорения a K , которое появляется в том
случае, если переносноеnдвижение оказывается вращательным:
t
a B 2 = a Bе + a Br + a K = a Bе + a Bе + a Br + a K ,
(2.55)
n
t
где a Bе и a Bе - соответственно нормальное ускорение точки В в переносном вращательном движении,
направленное по радиусу вращения точки к центру вращения А, и касательное ускорение, направленное
перпендикулярно радиусу вращения.
n
n
2
t
t
При этом a Bе = a B1 = ω1  AB ; a Bе = a B1 = ε1 ⋅  AB ; a Br = a21 = 0, т.к.υ 21 = const; aK = 2ω е ⋅ υ r = 2ω1 ⋅υ 21.
Направление кориолисова ускорения определяется поворотом в плоскости чертежа относительной

скорости υ21
в направлении переносной угловой скорости ω1 на 90 . Для положительной скорости
υ21 направление a K будет
Если учесть, что
n
t
a B 2 = a B3 = a B3 + a B3 ,
n
2
t
aB 3 = ω3 ⋅  3 ,aB 3 = ε3 ⋅  3 ,
то окончательно уравнение плана ускорений будет иметь вид
n
t
n
t
a B 3 + a B 3 = a B1 + a B1 + a K .
// BC ⊥ BC // AB ⊥ AB ⊥ AB
(2.56)

8. План ускорений механизма с гидроцилиндром

9. Графическое решение уравнения плана ускорений
Графическое решение уравнения состоит в определении неизвестных касательных
t
t
составляющих линейных ускорений aB1 и aB 3 .
Масштабный коэффициент плана ускорений K a можно назначить, исходя из наибольшего
известного значения ускорения. Пусть
n
aB3
Ka =
,
(2.57)
n
Z aB3
n
n
где Z a B 3 - отрезок, изображающий ускорение a B 3 на плане ускорений.
Тогда отрезки, пропорциональные значениям остальных известных
определятся как:
n
ускорений,
a B1
a
; Za K = K .
Ka
Ka
t
t
t
= K a ⋅ Z a B1 ; a B 3 ⋅ Z a B 3 .
n
Z a B1 =
t
a B1
Угловые ускорения звеньев 1-2 и 3 равны
t
t
aB3
a B1
ε1 =
; ε2 =
.
 AB
3
(2.58)
ε3
Для определения знака углового ускорения
следует перенести касательную
t
составляющую ускорения a B 3из плана ускорений в точку В механизма. Действие ускорения по
часовой стрелке определяет его отрицательный знак (рис. 2.10, а). Аналогично определяется
ε1 > 0.
направление ускорения

10. Линейные ускорения центров тяжести звеньев
Линейное ускорение центра тяжести S3 звена 3 определяется уравнением
n
(2.59)
t
aS3 = aS3 + aS3,
// CS 3 ⊥ CS 3
где aS 3 = ω3  CS 3 ; aS 3 = ε 3 ⋅  CS 3 .
Ускорение центра тяжести Sц цилиндра 1 определяется методом пропорционального
′
деления отрезка в1′в2 , изображающего абсолютное ускорение точки B1 , принадлежащей
цилиндру
 AS 
 AS 
(2.60)
a Sц = а В1  ц 
Z aSц = Z a B1  ц .
 АВ 
 АВ 

 или


Ускорение центра тяжести Sц поршня со штоком определяется уравнением
(2.61)
a Sn = a Sn1 + a K ,
n
2
t
// в1// в 2 ⊥ АВ
где a Sn1 - ускорение точки цилиндра 1, располагающейся в точке Sn , и определяется
aSц
аналогично
ускорению
 AS n 
(2.62)
a Sn1 = a B1


 AB 
или Z aSn1 = Z aB1  AS n .


 AB 
Для наглядности ускорения точек Sц и Sn показаны на рис. 2.10, г, который является
фрагментом плана ускорений и изображен не в масштабе.
Действительные значения ускорений центров тяжести звеньев определяются
уравнениями
a S 3 = K a ⋅ Z aS 3 ; a Sц = K a ⋅ Z aSц ; aSn = K a ⋅ Z aSn .