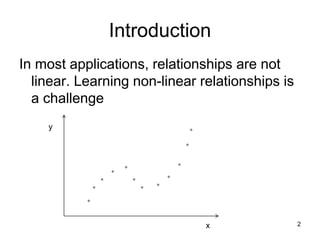
The document discusses the application of machine learning in civil engineering, focusing on learning non-linear relationships through feature space analysis. It emphasizes the importance of feature selection and provides examples of how feature vectors can be used to understand relationships in data, such as beam deflection and text classification. Additionally, it touches on regression with binary variables and the use of principal components for dimensionality reduction.

1. 1
Machine Learning in Civil
Engineering:
Learning in Feature Space
Dr. Benny Raphael
Professor
Civil Engineering Department
IIT Madras

2. Introduction
In most applications, relationships are not
linear. Learning non-linear relationships is
a challenge
2
x
y

3. Exercise: beam deflection
The deflection at the midspan of a beam of span L,
under a point load P at the midspan depends on
the Young’s modulus E, Moment of Inertia I, load
P and span L. If experiments are conducted
under different combinations of values of
parameters, how can the relationship between
deflection and the other parameters be
determined through regression?
3
What about the case with point load and UDL?

4. Feature space
One method of handling nonlinearity is by learning
in the feature space. The feature space contains
the set of all possible values for the “features”
extracted from raw data. If the original data
consists of vectors X = (x1, x2, … xn), we extract
features from the data as vectors of the form
(φ1(X), φ2(X), …, φm(X) ). The relationship
between the output variable y and the features
could be learnt by linear regression
4
Selection of good features is the most important phase of any
machine learning!

5. Feature vector in a quadratic
relationship
• x1
2
• x2
2
• x1 x2
• x1
• x2
5

6. Questions
• How many elements are in the feature vector when there
are N input variables in a quadratic relationship?
• How many elements are in the feature vector when there
are N input variables in a polynomial relationship of
degree m?
• How many elements in the feature vector of degree m?
• How many data points are needed for effective learning
in the above situations?
6

7. Exercise
• How many ways of distributing 10
chocolates to 4 children?
7

8. Regression with binary
variables
• Boolean relationships such as AND, OR
and XOR can also be learnt using
regression
8
X1 X2 Y
0 0 0
0 1 1
1 0 1
1 1 0

9. Exercise
What feature vector will you use for text
classification? (What features will you extract
from a text string in order to learn a relationship
between the text and some output variable).
Give examples of feature vectors extracted from
the data below. Add your own data to this set.
Explain how documents are classified using the
extracted feature vectors.
9
Data:
Text Score
Construction management 1
Management 0.5
Construction Industry 0.5
Construct buildings 0.3

10. Principal Components
• If you want to learn in a low dimensional
feature space, you can select a few
principal components as features
• Principal components are eigen vectors of
the covariance matrix
10

11. Further reading
• John Shawe-Taylor & Nello Cristianini,
2000. Support Vector Machines and other
kernel-based learning methods,
Cambridge University Press.
11