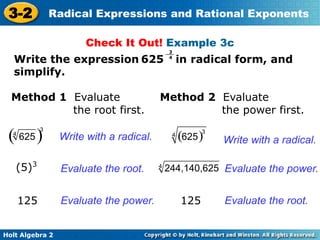
This document discusses radical expressions and rational exponents. It covers rewriting radical expressions using rational exponents, simplifying expressions with radicals and rational exponents, and properties of radicals and rational exponents such as the product, quotient, and power properties. Examples are provided to demonstrate evaluating radical expressions, simplifying expressions, and rationalizing denominators.