This document discusses the response of 1-degree-of-freedom systems to harmonic excitation. It covers: 1) The response of an undamped system, which has a steady state solution that is the sum of the homogeneous and particular solutions. The maximum amplitude is proportional to the force amplitude divided by the spring stiffness. 2) The response of a damped system, where the maximum amplitude depends on the frequency ratio and damping ratio. It is highest at resonance when the forcing frequency matches the natural frequency. 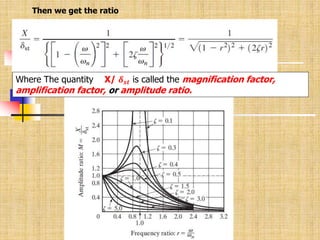3) Applications to damped systems subjected to harmonic base motion, rotating unbalance, or other periodic excitations. The ratio of response amplitude to static deflection is called the magnification or amplification factor

1. Forced vibration of 1DOF
• 1-Response of an un-damped system to harmonic excitation
•2- Response of a damped system to harmonic excitation
•
•Applications on Forced Damped
•Response of a damped system to harmonic base motion or
Excitation
• Response of a damped system to rotating unbalance

2. 1- Response of Forced Un-damped System Subjected to
(Harmonically excited vibration)
 In this part we will study the dynamic response of a single degree of
freedom system subjected to a harmonic force,
)
cos(
0 t
F
F 

)
cos(
0 t
F
kx
x
m 




 The general solution of the differential equation has two parts:
homogeneous solution and particular solution.
)
sin(
)
cos(
)
( 2
1 t
C
t
C
t
x n
n
h 
 

 The homogeneous [𝒙𝒉(𝒕)]solution will be on the form
:
m
k
n 

Let the excitation force is given by:
Then the equation of motion is given
by:

3. )
cos(
)
( t
X
t
xp 

 The particular [𝒙𝒑(𝒕)]solution (i.e Steady state Solution
)
cos(
0 t
F
kx
x
m 




)
cos(
)
( 2
0
t
m
k
F
t
x p 



 By substituting [𝑥𝑝(𝑡)] in the equation of
motion,
Let
So,
denotes the static deflection of the
mass under a force because 𝐹0is a
constant staticforce.
 Then the max amplitude of steady state Response is given by
 The amplitude of steady state solution is given by
Divid by
𝐹0
𝑘
= 𝛿𝑠𝑡

4. )
cos(
)
sin(
)
cos(
)
( 2
0
2
1 t
m
k
F
t
C
t
C
t
x n
n 







The general solution or total Response will be
in the form

5. The constants 𝐶1 𝑎𝑛𝑑 𝐶2 are obtained
from the initial conditions
)
cos(
)
sin(
)
cos(
)
( 2
0
0
2
0
0 t
m
k
F
t
x
t
m
k
F
x
t
x n
n
n 




 












0
0
)
0
(
)
0
(
x
x
x
x

 

The quantity X/ 𝛿𝑠𝑡 is called the magnification factor, amplification
factor, or amplitude ratio.
The max amplitude of steady state response
Divide by 𝛿𝑠𝑡

6. The harmonic response of the
system 𝑥𝑝(𝑡) is said to be in
phase with the external force.
The frequency ratio r =
𝝎
𝝎𝒏
has 3 cases

7. The harmonic response of the system 𝑥𝑝(𝑡) is
said to be 1800 out of phase with the external
force, as
𝜔
𝜔𝑛
→ 0, 𝑋 → 0 , thus at very high
frequency the response is close to zero.

8. This condition for which, the forcing frequency
𝜔 is equal to the natural frequency of the
system 𝜔𝑛, is called Resonance.

9. 2. Response of Forced damped System subjected to
(Harmonic excitation)

10. Forced damped System
The max amplitude is given by

11. The max value of steady state response of Forced damped System is given
by
Substitute in the above equation by the given values and
divide by 𝛿𝑠𝑡

12. Then we get the ratio
Where The quantity X/ 𝜹𝒔𝒕 is called the magnification factor,
amplification factor, or amplitude ratio.

13. Forced damped System