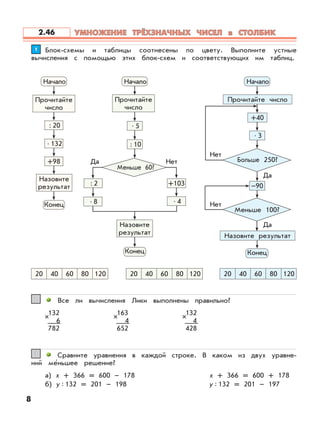
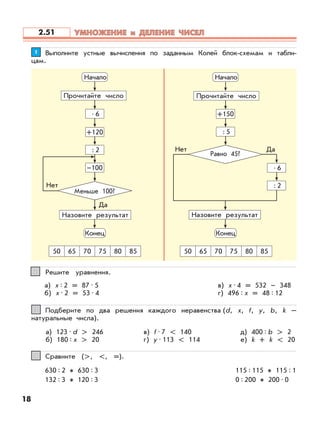
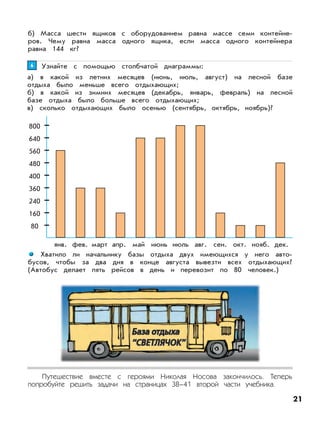
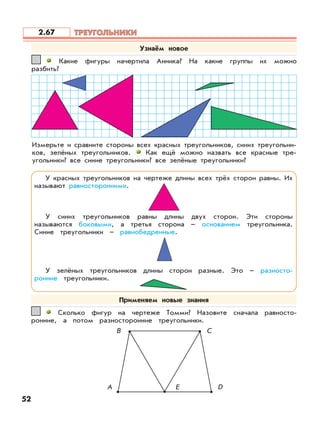
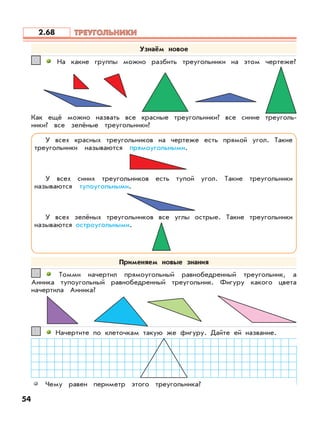
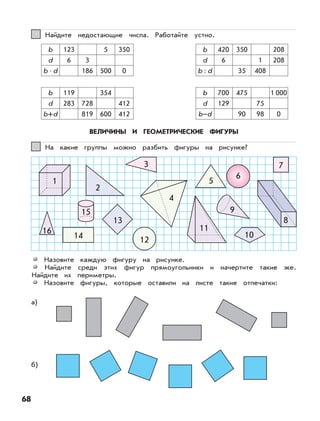
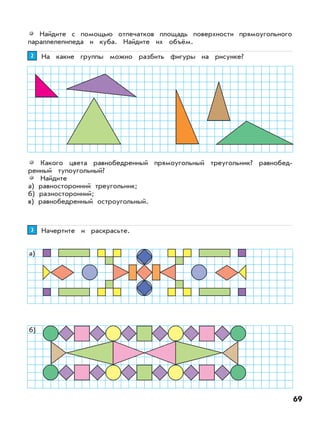
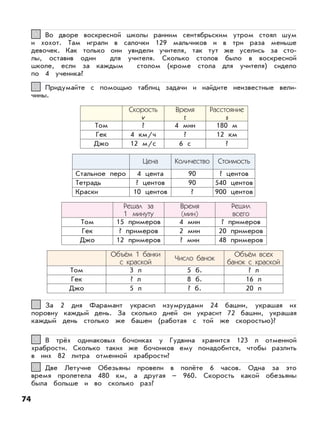
Документ описывает федеральный государственный образовательный стандарт для образовательной системы «школа 2100», акцентируя внимание на методиках и задачах по математике для 3 класса. Приведены примеры решений задач, а также практические подходы к обучению умножению и делению. Основное внимание уделяется формированию умений работать с числами и решать практические задачи.

1. Федеральный государственный образовательный стандарт
Образовательная система «Школа 2100»
Москва
2016
Т.Е. Демидова, С.А. Козлова, А.П. Тонких
Условные
обозначения
– этапы урока (организация де-
ятельности). Цветом обозначены
задания:
11 – на развитие предметных умений
(необходимый уровень);
11 – на развитие умений работать с
информацией: самостоятельно
осмысливать и использовать её
(повышенный уровень, – мак-
симальный уровень);
– на развитие умений общаться и
взаимодействовать (рекомендуются
для работы в паре, группе).
3 класс Часть 3

2. В роще на берегу озера 132 берёзы, это третья часть всех
деревьев, растущих на берегу озера. Сколько деревьев растёт на бере-
гу озера?
11
Лика записала решение так:
132•3 = (100 + 30 + 2)•3 = 300 + 90 + 6 = 396 (д.)
Объясните, как она нашла значение выражения.
Майя записала решение так:
132•3 = 396 (д.)
Сформулируйте ответ на основной вопрос урока.
132
3
396
Выполните умножение столбиком с объяснением.33
412•2 123•3 221•2 112•4
На большой берёзе около ручья Костя нашёл старое гнездо
аиста. В этом гнезде 122 толстые ветки, это в два раза меньше, чем
тонких. Сколько всего веток в этом гнезде?
Какое из этих выражений составлено к задаче?
122 + 122•2 (122 + 122)•2
Придумайте свою задачу к любому из этих выражений.
44
Знакомимся с основным вопросом урока
Как сделать вычисления??!
Узнаём новое
22
Письменно умножение выполняют, чаще всего используя запись
столбиком. Рассуждать при этом можно так:
Запишем числа в столбик: второй множитель под первым,
единицы под единицами;
умножим число 132 на 3 в столбик;
начинаем умножать с единиц: 2•3 = 6;
записываем в произведении в разряде единиц 6;
умножаем десятки: 3•3 = 9;
записываем в произведении в разряде десятков 9;
умножаем сотни: 1•3 = 3;
записываем в произведении в разряде сотен 3;
читаем ответ: 396.
Знак « » – это знак действия умножения.
132
3
396
Применяем новые знания
2
УМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИКУМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИК2.43

3. Выберите уравнение к задаче и решите его.55
х:231 = 500 – 498 231:х = 500 – 498 х:231 = 500 + 498
Утром к воротам турбазы вышла лосиная семья. Смотреть на неё на
площадку перед воротами сбежались 500 взрослых и детей. Через
некоторое время часть детей ушла в дом, и тогда на площадке
остались 498 человек. Сколько детей выбежали вначале на открытую
площадку смотреть на лосиную семью?
1
231
Расшифруйте слово. Хатку какого животного увидела Майя возле
ручья? Работайте в тетради.
66
408 – 260:130•204
(356 + 207) – 60•6:90
Ё
О
483 + 257 – 6•111
30•8:2 + (621 + 199)
Б
Р
74 559 74 940
Найдите объём прямоугольного параллелепипеда, если его длина
равна 30 м, ширина – 10 м, а высота – 2 м. Чему равна площадь
основания этого параллелепипеда?
77
Витя, Костя, Коля, Мишка, Майя и Лика отправились в дальний
поход к сосновому бору. Витя идёт перед Костей, а Коля – впереди
Мишки. Лика идёт позади Мишки, но перед Витей. Майя идёт позади
Кости. В каком порядке идут ребята?
88
Костя показал ребятам математический фокус. Он предложил им
сначала задумать трёхзначное число, у которого число сотен на 1
меньше числа единиц, а затем другое трёхзначное число, которое запи-
сывается теми же цифрами, но в обратном порядке, и вычесть из
большего числа меньшее. Какое число получится в результате? Верно
ли, что всегда будет получаться одно и то же число?
99
Выбираем задания и тренируемся
3

4. В сосновом бору ребята нашли 314 кустарничков черники и в
3 раза больше кустарничков брусники. Сколько кустарничков брусники
нашли ребята в сосновом бору?
11
Витя записал решение так:
314•3 = (300 + 10 + 4)•3 = 900 + 30 + 12 = 942 (к.)
Костя записал решение так: 314•3 = 942 (к.)
314
3
942
Объясните эти записи. Что нового появилось в алгоритме умножения?
Сформулируйте ответ на основной вопрос урока.
Выполните умножение столбиком с объяснением.33
452•2 123•4 121•6 86•4 92•2
Какие уравнения придумала Майя? Запишите и решите их:
а) неизвестное число разделили на 5 и получили разность 200 и 85;
б) на какое число нужно умножить 46, чтобы получить разность
чисел 100 и 8?
44
Знакомимся с основным вопросом урока
Как выполнить вычисления??!
22
Рассуждать можно так:
запишем числа в столбик: второй множитель под первым,
единицы под единицами;
умножим число 314 на 3 в столбик;
начинаем умножать с единиц: 4•3 = 12;
12 ед. – это 1 д. 2 ед.;
записываем в произведении в разряде единиц 2, а
1 д. запоминаем;
умножаем десятки: 1•3 = 3. После этого к 3 десяткам
прибавляем 1 десяток, полученный при умножении единиц.
Записываем в произведении в разряде десятков 4;
умножаем сотни: 3•3 = 9;
записываем в произведении в разряде сотен 9;
читаем ответ: 942.
314
3
942
Применяем новые знания
4
Выбираем задания и тренируемся
Узнаём новое
УМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИКУМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИК2.44

5. 5
В 12 рюкзаках мальчиков лежит по 4 банки тушёнки в каждом,
а в 8 рюкзаках девочек по 2 банки. Сколько банок тушёнки захва-
тили наши путешественники?
Лика задала Вите вопрос, ответить на который он сможет, найдя значение
выражения: 4•12 – 2•8.
Какой вопрос задала Лика?
55
От остановки автобуса до лесной опушки, где ребята решили устро-
ить привал, – 900 м. Они прошли 120 м по просёлочной дороге и
в 5 раз больше по лесной тропинке. Какое расстояние им осталось
пройти?
66
У путешественников есть два ведра: объёмом 4 л и 7 л. Смогут ли они
с помощью этих вёдер и большой бочки, врытой путниками у ручья, набрать
8 л воды, 5 л, 3 л, 6 л, 1 л, 2 л, 9 л?
Смогли бы они набрать такое же количество воды, если бы их
вёдра имели объём 4 л и 6 л?
77
Вечером у костра Костя рассказал друзьям старинную задачу.
Золотошвея разместила в комнатах своего дома 20 учениц так, как
показано на рисунке:
По вечерам она проверяла, чтобы в комнатах на каждой стороне
дома было 7 девочек. Однажды в гости к ним приехали 4 подружки.
а) Как им всем разместиться так, чтобы золотошвея опять насчи-
тала вдоль каждой стороны дома по 7 девочек?
б) На следующий день 4 девочки ушли провожать 4 подруг. Как
оставшимся девочкам разместиться так, чтобы золотошвея опять насчи-
тала вдоль каждой стороны дома по 7 девочек?
88
2 3 2
3 3
2 3 2
Расшифруйте название посёлка, где мастерицы вышивают жемчугом
и бисером. Работайте в тетради.
99
(362 + 208) – 50•4:20
516 + 287 – 2•214
Р
О
390:130•332 – 700С
342 + 568 – 112•4
221•2 + 123•3
Н
И
603 – 140:70•214Ф
296 375 175 560 811 462 375

6. 6
Вычислите. Какие вычисления вы смогли выполнить устно?
125•3 126•2 120•3 248•3 310•2 372•3
11
Сравните (>, <, =).22
3•224 224•4
131•7 101•7
191:1 202•1
0•230 0•23
Надо ли было искать значения этих выражений, чтобы выполнить
сравнение?
Какие из высказываний Кости истинные?
а) Число 106 является решением неравенства х•2 < 212.
б) Число 194 является элементом множества решений неравенства
х•3 > 482.
в) Число 302 является решением уравнения (х + 98)•2 = 600.
33
Какие из этих уравнений имеют одинаковое решение?44
х•2 + 196 = 600 (х + 98)•2 = 600 х•2 = 600 – 196
Как Майе поставить скобки и знаки действий между некоторыми
числами так, чтобы у неё получились верные равенства?
55
5 5 5 5 5 = 105
5 5 5 5 5 = 500
5 5 5 5 5 = 10
5 5 5 5 5 = 220
Решите задачи.
а) Возраст дуба, под которым путешественники построили свой шалаш, –
320 лет, а возраст берёзы, которая растёт рядом, в 2 раза меньше. На
сколько возраст берёзы меньше возраста дуба?
б) Рядом с шалашом растут 3 берёзы и 2 дуба. Каждая из этих
берёз в сутки поглощает из почвы 40 л воды, а каждый дуб в 2
раза больше. Сколько литров воды поглощают за сутки эти 3 берёзы
и 2 дуба?
66
Постарайтесь найти несколько способов.
УМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИКУМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИК2.45

7. 7
Какой кусок проволоки нужно взять Косте, чтобы сделать тре-
угольную подставку для котелка?
77
1
2
У путешественников есть консервы для
супа трёх видов: из курицы с рисом, из
говядины с вермишелью и из свинины с
горохом. Ещё есть четыре вида крупы для
каши на второе: гречка, пшено, овсянка и
перловка. На третье они могут сварить:
компот из яблок, компот из черники, зава-
рить чай из брусничных листьев.
Сколько дней они могут готовить обед
из трёх блюд так, чтобы ни в один из
этих дней обед не повторялся?
99
Какой длины эта проволока, если все размеры на рисунке уменьшены
в 10 раз?
Вычислите.88
315•2 + 123•3
124•8 – 78•4
97•(41 – 13•3)
(132•3 – 295)•5
45•9 – 29•7
205•4 + 37•3

8. 8
Блок-схемы и таблицы соотнесены по цвету. Выполните устные
вычисления с помощью этих блок-схем и соответствующих им таблиц.
11
•8
:2
•4
+103
Начало
•5
:10
Меньше 60?
Да Нет
Конец
Начало
+40
•3
–90
Больше 250?
Меньше 100?
Нет
Нет
Да
Да
Конец
20 40 60 80 12020 40 60 80 120 20 40 60 80 120
Начало
:20
•132
+98
Конец
Все ли вычисления Лики выполнены правильно?22
132
6
782
163
4
652
132
4
428
Сравните уравнения в каждой строке. В каком из двух уравне-
ний ме’ньшее решение?
33
а) х + 366 = 600 – 178
б) у:132 = 201 – 198
х + 366 = 600 + 178
у:132 = 201 – 197
Назовите
результат
Прочитайте
число
Прочитайте
число
Назовите
результат
Прочитайте число
Назовите результат
УМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИКУМНОЖЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ в СТОЛБИК2.46

9. 9
Какое из этих уравнений составлено к задаче?
Под древним дубом Костя нашёл глиняный кувшин с русскими моне-
тами 17 века: сначала там было 366 медных и несколько золотых
монет. Когда 178 медных алтынов из кувшина достали, в нём осталось
600 монет. Сколько золотых монет было в этом глиняном кувшине?
Сколько копеек составляют 178 алтынов, если 1 алтын = 3 коп.?
Придумайте задачу по уравнению х + 366 = 600 + 178 и схеме.
600 + 178
х 366
Сравните (>, <, =).44
2 р. 24 коп. 242 коп.
2 суток 72 часа
100 мм 1 дм
100 см2 4 дм2
1 дм3 100 см3
340 кг 3 ц 4 кг
600 с 6 мин
800 дм3 1 м3
Решите задачи.55
а) Лика во вторник помогала Косте чистить старинные монеты и за-
тратила на это от половины суток, а Майя в среду затратила на
такую же работу от третьей части суток. Сколько времени каждая
из них помогала Косте?
б) Костя подсчитал, что в кувшине хранилось 900 медных копеек. Хва-
тило бы этих денег владельцу клада на покупку парика, если парик
в 17 веке стоил 10 рублей?
1
3 1
2
Можно ли сделать такие рисунки одним движением руки, не обво-
дя ни одной линии дважды?
66
Вычислите.77
462•2 – 124•4
131•7 + 96•3
106•(131 – 128) – 32•5
47•(320 – 42•7) + 65
163•5 – 86•6
67•4 + 204•3
а) б) в)

10. Какую форму записи использовали мальчики?
Сформулируйте ответ на основной вопрос урока.
10
Как Лика и Майя искали значения выражений? Как они рассуж-
дали? Какие записи здесь пропущены?
84:4 = (80 + 4):4 = … 963:3 = (900 + 60 + 3):3 = …
22
Костя и Витя записали эти вычисле-
ния так:
33 963 3
9 321
6
6
3
3
0
–
–
–
84 4
8 21
4
4
0
–
–
Знакомимся с основным вопросом урока
Вычислите: 63:2; 264:2.11
Как выполнить деление??!
Узнаём новое
Такая запись называется деление уголком. Делимое 84 располо-
жили слева от «полочки-уголка». На «полочке» записан делитель 4,
а под «полочкой» будем записывать частное. Деление начинаем с
выбора первого неполного делимого. Движемся от старшего разряда
(слева направо). Мы делим на однозначное число, поэтому сначала
возьмём одну цифру делимого (первую слева). Сравним записанное
этой цифрой однозначное число с делителем. Если оно больше дели-
теля или равно ему, то именно это число и будет первым непол-
ным делимым. Случай, когда оно меньше делителя, будет рассмотрен
позже. Часто первое неполное делимое отделяют чёрточкой сверху.
После того как выбрано первое неполное делимое,
намечаем количество цифр в частном: их количество
на единицу больше, чем количество цифр справа от
первого неполного делимого (от чёрточки). В нашем
случае 8 > 4, значит, 8 и есть первое неполное
делимое. Справа от него стоит ещё одна цифра,
значит, в частном намечаем две цифры.
Делим 8 на 4 и получаем в частном 2. Два в
частном умножаем на делитель 4, получаем 8. Из 8
вычитаем 8, получаем 0, который по традиции не
записываем. Сносим следующую цифру делимого, полу-
чаем второе неполное делимое. Делим 4 на 4, полу-
чаем в частном 1. Один в частном умножаем на
делитель 4, получаем 4. Из 4 вычитаем 4, полу-
чаем 0. Последний нуль по традиции записываем.
Читаем ответ: 21.
84 4
8 21
4
4
0
–
–
–
84 4
••
ДЕЛЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛДЕЛЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ
на ОДНОЗНАЧНОЕ ЧИСЛОна ОДНОЗНАЧНОЕ ЧИСЛО
2.47

11. 11
Расскажите, как Витя разделил 963 на 3.44
Выполните деление двумя способами с объяснением и проверкой.55
682:2 999:3 844:4 468:2 693:3
Сравните уравнения в каждой строке. В каком из двух уравне-
ний бо’льшее решение?
66
а) х + 100 = 484:2
б) у•2 = 109 + 113
х + 100 = 484:4
у•2 = 109 + 313
Придумайте задачу по уравнению у•2 = 109 + 113 и схеме.
109 + 113
y y
Костя и Мишка собрались на рыбалку. Костя разложил поровну в
два пакета 228 горошин, а Мишка в три пакета – 336 горошин.
В чьём пакете горошин больше и на сколько? Сколько горошин мог
бы положить Костя в четыре таких же пакета?
77
Для ловли рыбы Витя и Коля хотят устроить 4 закидушки длиной
по 8 м каждая. Хватит ли им для этого двух мотков лески по
16 дм каждая и ещё одного мотка длиной 264 см?
88
Мальчики отправились ловить рыбу на прямоугольном плоту, пери-
метр которого равен 12 м. Каких размеров мог быть этот плот?
99
Применяем новые знания
Выбираем задания и тренируемся

12. Выполните деление с остатком.
5:4 3:2 8:3 10:4 12:5 53:7
Какие остатки могут получиться при делении чисел на 3? на 4? на 5? на 7?
11
Правильно ли Мишка выполнил деление? Как он мог при этом
рассуждать?
33
Как Костя и Витя искали значения выражений? Как они могли
при этом рассуждать? Какие записи здесь пропущены?
542:2 = (400 + 140 + 2):2 = … 434:2 = (400 + 20 + 14):2 = …
44
Лика и Майя записали эти вычисления так:55
542 2
4 271
14
14
2
2
0
–
–
–
434 2
4 217
3
2
14
14
0
–
–
–
Как они могли рассуждать? Сформулируйте ответ на основной вопрос урока.
Вспоминаем то, что важно для урока
Знакомимся с основным вопросом урока
Вычислите.
72:3; 723:3.
22
Как выполнить деление??!
Узнаём новое
42 3
3 14
12
12
0
72 3
6 24
12
12
0
–
–
–
–
Рассуждать можно так: надо число 542 разделить на 2.
Определяем количество цифр в частном. Первое непол-
ное делимое – 5 с. При делении сотен получатся сотни,
значит, первая цифра частного будет записана в разряде
сотен. Если число начинается с сотен, то это – трёхз-
начное число. Намечаем три цифры в частном.
Делим сотни: в делимом 5 с.; 5:2. Подбираем частное:
2 с. Записываем.
Делаем проверку: умножаем 2 с.•2 = 4 с.,
вычитаем 5 с. – 4 с. = 1 с. Одна сотня в остатке.
542 2
•••
12
ДЕЛЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛДЕЛЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ
на ОДНОЗНАЧНОЕ ЧИСЛОна ОДНОЗНАЧНОЕ ЧИСЛО
2.48

13. 13
Разделите 434 на 2 уголком с объяснениями.66
Выполните деление двумя способами с объяснением и проверкой.77
782:2 984:3 944:4 456:2 543:3
Выпишите и решите те уравнения, в которых последнее действие,
которым находят неизвестное, – действие деления.
88
х:6 = 210 – 90
х•6 = 210 – 90
5•х = 415 – 265
х:5 = 415 – 265
Чтобы пробежать расстояние от лагеря до ручья, Косте надо в 3
раза меньше времени, чем Майе. Сколько времени надо каждому из
них, чтобы пробежать расстояние от лагеря до ручья, если Майя тра-
тит на это на 20 с больше, чем Костя?
Выберите схему.
99
а)
К.
М.
с
с
с
б)
М.
К.
с
с
с
Сравниваем остаток с делителем: 1 < 2.
Делим десятки: в делимом 4 десятка и ещё осталось
разделить 1 сотню. 1 с. и 4 д. – это 14 д.,
14:2 = 7. В частном 7 д. Записываем. Делаем проверку:
умножаем 7 д.•2 = 14 д., вычитаем 14 – 14 = 0, оста-
ток 0 не записываем.
Делим единицы: в делимом 2 единицы. 2 ед.:2 = 1 ед.,
в частном 1 ед. Записываем. Делаем проверку:
умножаем 1•2 = 2, вычитаем 2 – 2 = 0, записываем в
остатке 0. Читаем ответ: 271.
542 2
4 271
14
14
2
2
0
–
–
–
Применяем новые знания

14. Коля не записал в равенствах остаток. Запишите верные равенства.
36:8 = 4 (ост. ...) 36:7 = 5 (ост. ...)
36:4 = 9 (ост. ...) 5:36 = 0 (ост. …)
К какому из равенств Витя составил уравнение, в котором остаток
обозначил буквой х?
36 – х = 8•4
Как мог рассуждать Витя, составляя это уравнение?
11
Все ли записи Майи верные? Исправьте ошибки, если они есть.
12:5 = 2 (ост. 1) 24:3 = 7 (ост. 3) 4:9 = 2 (ост. 1)
22
Выполните деление двумя способами с объяснением и проверкой.33
995:5
Витя: Костя:
741:3 380:4
Если вы не смогли найти значение выражения 380:4, по-
смотрите, как значение этого выражения искали Витя и Костя, и объ-
ясните, как они рассуждали.
44
380:4 = (360 + 20):4 = …. 380 4
36 95
20
20
0
–
–
Вспоминаем то, что важно для урока
Знакомимся с основным вопросом урока
Как выполнить деление??!
Узнаём новое
Сформулируйте ответ на основной вопрос урока.
Костя мог рассуждать так:
определяем количество цифр в частном. Намечаем
первое неполное делимое. Попробуем взять первое
неполное делимое 3 с.: 3:4 = 0 (ост. 3). Начинать
запись многозначного числа с 0 нельзя, значит, 3 с. не
подходят.
Запись частного начнётся с десятков, поэтому в част-
ном намечаем две цифры.
Делим десятки: 38 д.:4. Частное: 9 д. Записываем.
Делаем проверку: умножаем 9 д.•4 = 36 д.,
вычитаем 38 д. – 36 д. = 2 д. Два десятка в остатке.
Сравниваем остаток с делителем: 2 < 4.
Делим единицы: 2 д. – это 20 ед. 20 ед.:4 = 5 ед.
Записываем остаток 0, в частном записываем 5 ед.
Читаем ответ: 95.
14
380 4
36 95
20
20
0
–
–
380 4
••
ДЕЛЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛДЕЛЕНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ
на ОДНОЗНАЧНОЕ ЧИСЛОна ОДНОЗНАЧНОЕ ЧИСЛО
2.49

15. 15
Вычислите с объяснением и проверкой.
72•5 252•3 112•4 252:4 474:3
55
Решите задачу, построив и заполнив схему.
Путешественники за пятницу, субботу и воскресенье собрали 980 ягод
земляники. В пятницу и субботу они собрали 725 ягод. Сколько ягод
они собирали в каждый из этих дней, если в субботу они собрали
на 123 ягоды больше, чем в воскресенье?
66
я.
пятница суббота воскресенье
я.? я.? я.?
я.
я. большена
Витя и его друзья занимались сборами и уборкой поляны. В пят-
ницу они занимались этим 40 минут, в субботу на 360 минут больше,
а в воскресенье в 4 раза больше, чем в пятницу. Сколько всего
часов затратили на сборы и уборку поляны Витя и его друзья?
77
Костю и Мишу отправили к ручью за водой. Как им набрать из ручья
с помощью пятилитрового и семилитрового вёдер и вкопанной у ручья боч-
ки ровно 3 л воды, чтобы заполнить этой водой фляжки всех шести путе-
шественников?
Смогли бы они выполнить это задание, если бы их вёдра были объёмом
6 л и 8 л?
88
Применяем новые знания
Выбираем задания и тренируемся

16. 16
Выполните деление с остатком и сделайте проверку.11
6:5
8:3
9:4
12:5
24:3
5:6
56: 6
29:14
Все ли вычисления Лика сделала верно? Запишите правильные
решения.
22
625 5
5 123
12
10
15
15
0
–
–
–
564 6
0 094
56
54
24
24
0
–
–
–
84 3
6 271
24
21
3
3
0
–
–
–
Все ли вычисления сделаны верно? Почему у Кости, Вити и
Мишки получились разные значения выражений?
33
684:(2 + 2)•2 = 342 (684:2 + 2)•2 = 688
684:2 + 2•2 = 346
300:2 + 3•5 = 300 300:2 + 3•5 = 165
300:2 + 3•5 = 765
Спишите. Расставьте скобки так, чтобы равенства были верными.44
Решите задачи.55
а) Путешественники возвращались из похода трое суток. Восемнадцать
часов они шли пешком, по дороге они делали привалы, которые со-
ставили времени движения пешком, несколько часов ехали на попут-
ной машине и часть всего времени сплавлялись по реке на плоту.
Сколько часов они ехали на попутной машине?
б) Костя отдыхал после похода 8 часов, Витя в два раза больше, а
Лика часть того времени, что отдыхали Костя и Витя вместе. Сколь-
ко времени отдыхала после похода Лика?
1
2
1
2
1
6
УМНОЖЕНИЕ и ДЕЛЕНИЕ ЧИСЕЛУМНОЖЕНИЕ и ДЕЛЕНИЕ ЧИСЕЛ2.50

17. 17
в) Костя, Витя и Коля решили расчистить спортивную площадку и огоро-
дить её тремя рядами верёвки. Сколько им надо взять для этого мот-
ков верёвки по 20 м каждый, если длина площадки 18 м, а ширина
составляет часть длины?1
6
У Лики и Майи есть кусок ткани такой формы:66
Они хотят разрезать его на 4 равные части и сшить квадратный навес от
солнца. На какие части они могут разрезать этот кусок ткани?
Костю послали к ручью за водой с двумя вёдрами: объёмом 5 л
и 7 л и попросили принести ровно 4 л воды. Возле ручья нет бочки,
в которой можно накапливать воду, её можно только переливать из
ведра в ведро и выливать в ручей.
Костя начал решать эту задачу, рассуждая с конца (обратным
ходом).
«Если я хочу собрать ровно 4 л воды в семилитровом ведре, то мне
нужно наполнить это ведро и отлить из него ровно 3 л воды.
Сделать это можно с помощью пятилитрового ведра, в котором
налито ровно 2 л воды. Значит, сначала мне нужно собрать в пятилит-
ровом ведре ровно 2 л воды. Из полного семилитрового ведра я вылью
воду в пустое пятилитровое, в семилитровом ведре у меня останется
ровно 2 л воды. Вылью воду из пятилитрового ведра и перелью в
него 2 л из семилитрового...»
Закончите рассуждения Кости.
77
Вычислите.88
82•6 – 852:4
263•3 + 392:7
426:2•4 – 198
213•2:3 + 269
565:5•3 + 61
600 – 144:3•5

18. 18
Выполните устные вычисления по заданным Колей блок-схемам и табли-
цам.
11
Нет
50 65 70 75 80 85 50 65 70 75 80 85
Начало
•6
+120
:2
–100
Конец
Меньше 100?
Да
Нет
Начало
+150
:5
•6
:2
Конец
Равно 45?
Да
Решите уравнения.22
а) х:2 = 87•5
б) х•2 = 53•4
в) х•4 = 532 – 348
г) 496:х = 48:12
Подберите по два решения каждого неравенства (d, x, f, y, b, k –
натуральные числа).
33
а) 123•d > 246
б) 180:x > 20
в) f•7 < 140
г) y•113 < 114
д) 400:b > 2
е) k + k < 20
Сравните (>, <, =).44
630:2 630:3
132:3 120:3
115:115 115:1
0:200 200•0
Прочитайте число Прочитайте число
Назовите результат Назовите результат
УМНОЖЕНИЕ и ДЕЛЕНИЕ ЧИСЕЛУМНОЖЕНИЕ и ДЕЛЕНИЕ ЧИСЕЛ2.51

19. 19
I
II
Какие из высказываний Кости истинные?
а) Если некоторые числа разделить на себя, то получится единица.
б) Произведение всякого числа на 0 равно 0.
в) Частное любого числа и единицы равно единице.
55
Решите задачи.66
а) Накануне прощального праздничного ужина в столовую привезли
125 кг муки. На приготовление тортов израсходовали 1
5
часть муки,
а из 1
10
части остальной муки приготовили кулебяки с мясом. Сколь-
ко получилось кулебяк, если из каждого килограмма муки получается
3 кулебяки?
б) Для праздника Лика и Майя купили 8 гирлянд из цветных лампочек
по одинаковой цене. Лика заплатила за покупку 190 рублей, а Майя
570 рублей. Хватит ли Косте для покупки трёх таких же гирлянд 250
рублей?
Три девочки, каждая со своей мамой, украшали площадку перед
входом в кинозал. Сколько человек украшали площадку?
Сколько решений имеет эта задача?
77
Костю попросили выпустить сигнальную ракету в начале праздника
через 20 минут после условленного времени. Первый циферблат пока-
зывает начало отсчёта.
Помогите Косте по второму циферблату узнать, сколько времени про-
шло. Пора ему пускать сигнальную ракету?
88

20. 20
При лесной базе отдыха есть легковая машина и автобус. За один
рейс легковая машина перевозит четверых человек, а автобус 70.
В Москву надо отправить 192 ребёнка и 88 взрослых.
На какие вопросы хотел ответить начальник лесной базы отдыха, со-
ставляя выражения:
192:4; 88:4; (192 + 88):4; (192 + 88):70;
(192 + 88):4 – (192 + 88):70?
11
Вычислите.
102 + 102:6; 800 – (95 + 95•5); 72:6•3.
Придумайте задачу к любому из этих выражений.
22
Лобзик помогал начальнику лагеря нести от дома к машине вче-
рашнюю газету. При этом он сделал 5 прыжков по 9 дм каждый по
направлению к машине, потерял по дороге газету и пробежал назад
180 см, схватил газету и бежал с ней за начальником лагеря ещё
15 м. Какое расстояние пробежал Лобзик? Донёс ли он газету до
машины, если машина стояла в 20 метрах от дома?
33
Вычислите. Выразите результат
а) в метрах: в) в метрах кубических:
120 дм•5 – 123 м:3; 250 дм3•3 + 125 дм3•2.
б) в дециметрах, сантиметрах и миллиметрах:
569 мм + 30 мм•7:5 – 2 м;
44
Решите уравнения.55
б) х:7 = 144:6а) х•6 = 144•7
С помощью какого уравнения и какой схемы шофёр автобуса
может решить каждую задачу?
х кг
144 кг
а) б)
144 кг
х кг
а) Масса шести рюкзаков равна 144 кг. Чему равна масса семи таких
же рюкзаков?
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.52

21. 21
б) Масса шести ящиков с оборудованием равна массе семи контейне-
ров. Чему равна масса одного ящика, если масса одного контейнера
равна 144 кг?
Узнайте с помощью столбчатой диаграммы:
а) в какой из летних месяцев (июнь, июль, август) на лесной базе
отдыха было меньше всего отдыхающих;
б) в какой из зимних месяцев (декабрь, январь, февраль) на лесной
базе отдыха было больше всего отдыхающих;
в) сколько отдыхающих было осенью (сентябрь, октябрь, ноябрь)?
66
80
160
240
360
400
480
560
640
800
янв. фев. март апр. май июнь июль авг. сен. окт. нояб. дек.
Хватило ли начальнику базы отдыха двух имеющихся у него авто-
бусов, чтобы за два дня в конце августа вывезти всех отдыхающих?
(Автобус делает пять рейсов в день и перевозит по 80 человек.)
Путешествие вместе с героями Николая Носова закончилось. Теперь
попробуйте решить задачи на страницах 38–41 второй части учебника.

22. 22
Всё лето, каждую субботу и воскресенье, папа и мама обещают
устраивать «День семьи» с походами и развлечениями. Какие даты будут
у этих праздников?
55
На какой день недели в этом году приходится 1.09? Если 1.09
попадает на субботу или воскресенье, то какого числа начнётся учеб-
ный год? Сколько дней будут длиться летние каникулы?
44
29.05 начнутся летние каникулы. Какой это будет день недели?33
Уроки начинаются в 8 ч 30 мин. На потягивание в постели уходит
15 мин, столько же на утреннюю гимнастику. Чистка зубов, умывание
и завтраки вместе занимают столько же времени, сколько утреннее
потягивание и утренняя зарядка вместе. Сборы в школу занимают поло-
вину всего времени, которое затратили на потягивание, гимнастику, умы-
вание и завтрак. Дорога в школу занимает 40 мин. Во сколько надо
встать, чтобы не опоздать в школу в последний день учебного года?
22
Сколько времени показывают часы на рисунке?11
Сколько времени будут показывать часы, когда минутная стрелка
сделает четыре полных оборота?
XII I
II
III
IV
VVI
VII
VIII
IX
X
XI
ПОСЛЕДНИЙ ЗВОНОК и ЛЕТНИЕПОСЛЕДНИЙ ЗВОНОК и ЛЕТНИЕ
КАНИКУЛЫКАНИКУЛЫ
Путешествие 6

23. 23
Если вы не можете сразу ответить на все эти вопросы, значит, вам
предстоит ещё одно и последнее в этом году путешествие вместе с геро-
ями книги «Пе’ппи Дли’нныйчуло’к», которую написала шведская писательница
А’стрид Ли’ндгрен.
Герои этой книги – брат и сестра, которых зовут То’мми и А’нника. Им
столько же лет, сколько и вам, и они тоже учатся в школе, только швед-
ской, но задачи решают такие же.
А ещё в этом путешествии с вами будет Пеппило’тта-Виктуали’на-Рольгар-
ди’на, а короче – Пеппи Длинныйчулок, её обезьянка по имени господин
Ни’льсон, лошадь, которую она иногда носит на руках, и Пеппин папа –
негритянский король Эфрои’м Длинныйчулок.
Желаем вам весёлого путешествия и удачи в поисках способов решения
новых задач!
В лагере отдыха часто ходят в походы. Представьте себе, что в
одном из таких походов команде из 5 взрослых и 15 ребят придётся
переправляться через реку на лодке, которая так мала, что на ней
могут переправиться только двое ребят или один взрослый. Как всем
переправиться через реку?
99
Автобус должен был проехать расстояние от остановки до места
назначения, равное 420 км, за 6 часов. Но первые два часа из-за
сильного дождя он ехал со скоростью на 10 км/ч меньше, чем соби-
рался. Посоветуйте водителю автобуса, с какой скоростью он должен
проехать оставшийся путь, чтобы прийти в пункт назначения без опо-
здания.
88
Автобус, который идёт на вокзал, остановился в 1 км от дома.
Мальчик ходит со скоростью 100 шагов в минуту. Каждый его шаг
равен 5 дм. Когда ему надо выйти из дома, чтобы прийти за
15 мин до отправления автобуса, который уезжает в 14 ч 30 мин?
Если он придёт к автобусу за 15 мин до отправления, то хватит
ли у него времени, чтобы купить мороженое в киоске, который рас-
положен в 500 метрах от автобуса, если будет идти с той же ско-
ростью, что шёл к автобусу, а на покупку мороженого ему нужно
5 минут?
77
Поедете ли вы к кому-нибудь в гости? Назовите даты дней отъ-
езда и приезда.
66

24. На каждом буйке записано число. Запись сделана и арабскими,
и римскими цифрами.
11
Как записать римскими цифрами числа: 35, 52, 60, 300, 600?
Прочитайте записи Пе’ппи Дли’нныйчуло’к.
В стране Весе’лии CХХV жителей. Среди них LХХ маленьких весе-
лян. На острове DCC кокосовых пальм и DCCL хлебных деревьев.
К приезду капитана Длинныйчулок веселяне приготовили CХ ожерелий из
акульих зубов.
22
Как Томми записать римскими цифрами числа: 32, 27, 115?33
Пе’ппи учила Момо’ и Моа’ну считать. Они выложили палочками на
песке несколько равенств. Верные ли это равенства? Как им перело-
жить по одной палочке в неверных равенствах так, чтобы равенства
стали верными?
44
ХХII + ХVII = ХХХIV
Х + III = ХI
– ХХ = XX
Х + Х = ХV
ХIV – VI = VIII
X – I = XII
Постарайтесь найти несколько способов.
24
Узнаём новое
Число 35 записывается так: ХХХV;
число 52 записывается так: LII, так как 50 – это L;
число 60 записывается так: LХ;
число 300 записывается так: CCC, так как 100 – это С;
число 600 записывается так: DC, так как 500 – это D.
Применяем новые знания
ЗАПИСЬ ЧИСЕЛ РИМСКИМИ ЦИФРАМИЗАПИСЬ ЧИСЕЛ РИМСКИМИ ЦИФРАМИ2.53

25. Какое время показывают часы на капитанском мостике яхты
«Попрыгу’нья», в хижине короля Эфрои’ма и наручные часы господина
Ни’льсона?
Какие из этих часов идут правильно, если сейчас 3 ч 15 мин дня?
55
Чьи часы спешат? На сколько? Чьи часы отстают? На сколько?
«Попрыгунья» вышла из бухты Веселии в начале октября и за-
шла в шведскую гавань в конце декабря этого же года. Сколько
месяцев она была в пути, если месяцы в году располагаются по поряд-
ку так: январь, февраль, март, апрель, май, июнь, июль, август, сен-
тябрь, октябрь, ноябрь, декабрь?
Пронумеруйте римскими цифрами январь, август, октябрь, декабрь.
66
Пеппило’тта жонглирует перед веселянами шестнадцатью одинаковыми
по виду золотыми монетами. Одна из них легче остальных. Сколько
взвешиваний на весах без гирь надо сделать А’
ннике, чтобы найти эту
монету?
77
Вычислите.88
I
II
III
IV
V
Яхта Господин
Нильсон
Хижина
VIVII
VIII
IX
X
XI
XII
I
II
III
IV
V
VIVII
VIII
IX
X
XI
XII
I
II
III
IV
V
VIVII
VIII
IX
X
XI
XII
595:7 + 96•7
106•5 + 488:4
102:6•8 + 74
165:5•8 – 195
400 – 224:7•9
84•(570 – 113•5)
(27 + 95)•5:2
798:(463 – 456) + 286
(569 + 223):6•7
25
Выбираем задания и тренируемся

26. 26
Отрезок на рисунке А’нники изображает год. Он разделён на не-
сколько частей. Каждая часть – один месяц. Месяцы пронумерованы
римскими цифрами.
11
I II III IV V VI VII VIII IX X XI XII
Цветом на рисунке обозначены времена года: белым – зима, голубым –
весна, зелёным – лето, жёлтым – осень.
Сколько месяцев в году? Как называется I месяц года? V месяц?
Х месяц? Назовите все зимние месяцы, весенние, летние, осенние.
Сколько дней в каждом времени года? Сколько дней в году?
Сколько дней в високосном году?
22
Назовите и запишите даты рождения ваших друзей.33
В году, следующем за тем, когда То’мми и А’нника познакоми-
лись с Пеппи, они учились 170 дней, 60 дней путешествовали на яхте
«Попрыгунья», а остальное время провели в стране Веселии. Сколько
времени они провели в Веселии?
44
Пеппи появилась на вилле «Курица» в полдень 26 сентября, а
26 мая следующего (не високосного) года в полдень покинула её вмес-
те с Томми и Анникой. Сколько суток она провела на своей вилле?
55
Узнаём новое
В году 12 месяцев: I – январь, II – февраль, III – март, IV –
апрель, V – май, VI – июнь, VII – июль, VIII – август, IХ – сен-
тябрь, Х – октябрь, ХI – ноябрь, ХII – декабрь.
В I, III, V, VII, VIII, Х, ХII месяцах – по 31 дню.
В IV, VI, IХ, ХI – по 30 дней.
Во II – 28 дней, а каждый четвёртый год (високосный) – 29
дней.
День Победы мы отмечаем 9.05 каждого года.
Применяем новые знания
КАЛЕНДАРЬКАЛЕНДАРЬ2.54

27. На полке в капитанской каюте стояли судовые журналы. На каждом
журнале римскими цифрами был обозначен год плавания (с I по XXX).
После схватки с пиратами некоторые из них пропали. Журналов с
какими номерами нет в каюте? (Дайте ответ при помощи рисунка.)
66
Сможет ли Пеппи найти рецепт молодильных пилюль, если он был
записан в судовом журнале за пятнадцатый год плаванья?
Когда капитана Эфрои’ма во время ужасной бури волна смыла за
борт, а потом вынесла на остров Южного моря, он отправил письмо
в бутылке. Что в нём записано? (Капитан использовал шифр по пра-
вилу: прибавь четыре. В этом шифре буквы имеют номера: А – V,
Б – VI, В – VII, …)
XIV, XXXI, XIV, XXIV, X XVIII, X, XIX, XXXVII XIX, V
XVI, XX, XVI, XX, XXIII, XX, VII, XXXIII, XXVII
XX, XXIII, XXIV, XXII, XX, VII, V, XXVII.
77
Положите в непрозрачную коробку 4 одинаковые на ощупь картон-
ные карточки: 3 белые и 1 чёрную. Проведите такой опыт: возьмите
из коробки не глядя одну карточку и назовите её цвет. При проведе-
нии этого опыта может произойти одно из двух событий: «вынута белая
карточка» или «вынута чёрная карточка». Можно также сказать для крат-
кости: произошло событие Б или событие Ч.
Положите вынутую карточку обратно в коробку и проведите такой
же опыт несколько раз, записывая, какие события происходили в этих
опытах.
Можете ли вы заранее (до того, как проведёте опыт) сказать,
какое из событий произойдёт?
99
Вычислите.88
92•7 – 768:8
208•4 + 195:3
(312:3 – 89)•9
132:2•8 – 299
(35•7 – 199•3)
106•(570 – 63•9)
(900 – 405):5•7
762:(893 – 887)
(400 – 205:5)•2
Выбираем задания и тренируемся
27

28. 28
11
В том году, когда Пеппи Длинныйчулок впервые оказалась в государстве
Веселия, она подарила жителям Веселии этот календарь.
Помогите им с помощью этого календаря ответить на вопросы.
а) На какой день недели пришёлся в том году День рождения госу-
дарства Веселия, если его празднуют 5.05 каждого года?
б) Каждое первое воскресенье месяца в Веселии – день карнавала.
Перечислите даты веселянских карнавалов того года.
в) Каждую пятницу в августе того года веселяне варили ананасовые
дольки в меду. К каким датам им надо было приготовить мёд и
ананасы?
Расскажите, пользуясь календарём из задания № 1, какое число
и месяц наступили в том году, когда
а) через 87 дней после начала года веселяне устроили большую охоту
на тигровых акул;
б) через 125 дней после начала года капитан Эфроим привёз на
берега Веселии принцессу Пеппилотту;
в) через 6 месяцев после начала года Томми, Анника и Пеппи спа-
сли веселян от нападения бандитов Джима и Бука?
22
Каждый год с 11 марта по 19 мая веселяне отправляются в
экспедицию на острова Южного моря. Сколько дней длится эта экс-
педиция?
33
КАЛЕНДАРЬКАЛЕНДАРЬ2.55

29. В экспедицию отправилось 60 каноэ. У каждой из этих лодок был
свой судовой номер. Из экспедиции не вернулись лодки под номе-
рами: LX, LV, XII, VII, IV, IX, III, XVII, I, II, V, X. Они были пода-
рены жителям дальних островов. Сколько лодок вернулось из экспеди-
ции? Какой наибольший номер у вернувшихся лодок? наименьший?
44
Для устройства свинофермы на одном из островов Южного моря
капитан Эфроим организовал отлов диких свиней. В нём участвовало
всё взрослое население Веселии: 30 женщин и 26 мужчин, и в 5 раз
больше детей, чем взрослых. Диких свиней на этом южном острове
было в два раза меньше, чем охотников. Сколько диких свиней было
на южном острове?
55
Расшифруйте слово, и вы узнаете название ближайшего родственни-
ка динозавров, нападение которого пришлось во время охоты отразить
капитану Эфроиму и его охотникам. Работайте в тетради.
66
(108 + 392) – 225:5
(765 – 279): 6 + 119
И
Д
(339:3 + 97)•4:2
890 – (475:5 + 205)
К
Р
52:13•100 + 67Л48:24•246:4О
420 590 123 420 123 200 455 467
Проведите один раз такой же опыт, как в задании № 9 на стр. 27.
В этом опыте может произойти только два события: «достали белую
карточку» или «достали чёрную карточку». Сказать заранее, какая имен-
но карточка будет вынута (какое событие произойдёт), невозможно.
Такие опыты называются случайными опытами. Событие, которое при
проведении случайного опыта может произойти, а может и не прои-
зойти, называется случайным событием.
Произойдёт случайное событие или нет, выяснится только после про-
ведения случайного опыта.
Можно ли из коробки, где лежат только чёрные и белые кар-
тонные карточки, достать зелёную карточку? шоколадку?
Такое событие произойти не может, его называют невозможным.
77
29

30. Томми, Анника и Пеппи записали все известные им единицы
измерения величин. На какие группы их можно разбить?
Литр, секунда, минута, дециметр, квадратный метр, месяц, кубический
дециметр, час, миллиметр, метр, сутки, килограмм, неделя, год, век.
Все ли единицы времени, записанные здесь, вам знакомы? Знаете ли
вы, сколько лет длится век? Какие промежутки времени измеряют века-
ми?
Назовите все известные вам элементы множеств «Единицы времени»,
«Единицы длины», «Единицы объёма», «Единицы массы», «Единицы пло-
щади».
11
Анника нарисовала для Момо’ и Моа’ны часть ленты времени.
Помогите им с помощью этого рисунка ответить на некоторые вопро-
сы.
33
XV в. XVI в. XVII в.XVIII в. XIX в. XX в. XXI в.
а) Крокодилу 100 лет. Выразите его возраст в веках.
б) Секвойе, которая растёт в национальном парке Редвуд в США, 7
веков. Выразите её возраст в годах.
в) Мы живём в XXI веке. За последние 3 столетия на Земле исчез-
ли 36 видов млекопитающих и 94 вида птиц. За сколько веков это
произошло? В каком веке они начали исчезать?
Моа’на нарисовала часть ленты времени, на которой точками
отметила годы рождения членов своей семьи.
22
В каком веке родился каждый из родственников Моаны? В каком году
этого века? На сколько лет бабушка Моаны младше дедушки? Папа
старше мамы? Моана старше своего брата?
Придумайте рассказ о себе, отвечая на вопросы:
В каком веке вы живёте? В каком веке родились? В каком году века это
было? Какая дата вашего рождения?
10
XX век XXI век
20 30 40 50 60 70 80 90 10 20 30 40
Дедушка Бабушка Папа Мама Моана Брат Моаны
Вспоминаем то, что важно для урока
Узнаём новое
Большие (длительные) промежутки времени измеряют веками.
Век равен 100 годам, поэтому век иногда называют столетием.
Применяем новые знания
30
ЕДИНИЦЫ ИЗМЕРЕНИЯ ВРЕМЕНИ. ВЕКЕДИНИЦЫ ИЗМЕРЕНИЯ ВРЕМЕНИ. ВЕК2.56

31. 31
Три друга: Мья’мба, Бо’но и То’мми родились в три последние
дня февраля одного и того же високосного года. День рождения
То’мми 28.02. Он старше Мья’мбы и моложе Бо’но. Какие даты ро-
ждения у Мья’мбы и Бо’но?
44
а) Анника, Момо и Моана в 8 ч 15 мин утра отправились на
день рождения к старейшине соседнего острова. Два часа они пре-
одолевали на лодке пролив между островами, этого времени они
пробирались между прибрежными скалами и ещё 45 минут шли пеш-
ком к деревне, где живёт старейшина. В какое время они пришли в
деревню?
б) Хижины, стволы пальм и свои причёски жители деревни украшали
цветами 2 ч 15 мин и закончили эту работу в 12 ч 30 мин. В какое
время они начали украшать хижины, стволы пальм и свои причёски?
в) Праздник начался в 4 часа дня с соревнования между воинами пле-
мени. Во сколько закончились соревнования, если они длились 75 минут?
55
1
3
Расшифруйте слово, и вы узнаете, что подарили Анника, Момо и
Моана старейшине. Работайте в тетради.
66
Задумайте двузначное число, вычтите из него 5. Результат умножьте
на 4, прибавьте задуманное число, прибавьте ещё 20 и результат раз-
делите на 5.
Какое число получилось? Можно ли, зная результат, отгадать заду-
манное число?
77
(678 – 675)•125:5
60:15•235 – 298
Е
Р
372:6 + 123•3
(245:245 + 699):5
Х
М
125:5 + 23•9Т48:12•78 – 278Н
502 – (95•4 – 105)О
431 642 227 34 227 140 75 232 642
г) В самом начале ХVII века население островов Южного моря было
в два раза меньше, чем в самом конце XIX. За сколько лет насе-
ление островов Южного моря увеличилось в два раза?
д) В самом конце XIX века на островах Южного моря было в два
раза больше деревьев, чем в самом начале ХХI. За сколько лет
уменьшилось в два раза число деревьев на островах Южного моря?
Выбираем задания и тренируемся

32. 32
Сравните (>, <, =).22
10 дм 100 см 1 м 1000 мм 1000 м 3 км
Пеппи и матросы с «Попрыгуньи» решили устроить соревнования
по гребле. Им надо разметить дистанцию в 1 км. Сколько буйков им
надо приготовить, если буйки будут установлены через каждые 100 м?
Сколько таких же буйков им понадобится, чтобы разметить дистанцию
в 10 км?
33
1 км1 км
600 м
1 век 100 лет
100 дм2 10 м2
1 000 дм3 1 м3
1 л 1 дм3
100 кг 1 ц
1 дм3 999 см3
100 коп. 3 руб.
1 дм2 100 см2
1 000 м 1 км
Сравните (>, <, =).11
Узнаём новое
Смогли ли вы выполнить задание полностью? Меры каких величин вы
сравнивали? Что означает запись 1 км?
Какая величина может быть измерена километрами? Можно ли сравни-
вать метры и километры?
Километр – ещё одна единица измерения длины.
В одном километре 1 000 метров. Километрами измеряют большие
расстояния, например, расстояние, пройденное туристами в походе,
длину пути поезда, корабля или самолёта.
1 км = 1 000 м
1 м = 10 дм
1 дм = 10 см
1 см = 10 мм
1 м = км
1 дм = м
1 см = дм
1 мм = см
1
1000
1
10
1
10
1
10
Применяем новые знания
ЕДИНИЦЫ ИЗМЕРЕНИЯ ДЛИНЫ. КИЛОМЕТРЕДИНИЦЫ ИЗМЕРЕНИЯ ДЛИНЫ. КИЛОМЕТР2.57

33. 33
Жители острова делают каноэ на
берегу океана, а деревья для них добыва-
ют в Корабельной роще. Помогите Пеппи
с помощью плана, составленного Эфрои-
мом, узнать, на какое расстояние ей нужно
перенести поваленное дерево из Корабельной
рощи на берег океана.
44
Аннику попросили позвать на берег
лучшего мастера по изготовлению каноэ.
Его хижина на плане деревни расположена
у острого угла ограды. Какая это хижина?
(Назовите фигуру, которой она обозначена.)
55
В Корабельной роще 492 железных дерева, древовидных папорот-
ников в 6 раз меньше, а мангровых деревьев на 605 больше, чем
папоротников. Сколько мангровых деревьев растёт в Корабельной роще?
66
Расшифруйте название цветов, которые растут на стволах деревьев
в Корабельной роще. Работайте в тетради.
77
(202 + 478) – 480:6
(365 + 277):6 + 119
Р
Д
(448:4 + 88)•5:2
900 – 175:5 + 105
Х
И
96:12•100 + 67Е56:28•108:4Я
60:30•380:4О
190
Роща
600 500 970 226 867 54
На рисунке изображены пути, ведущие от Корабельной рощи к
озеру через деревню.
Сколько путей ведёт от рощи к деревне? от деревни к озеру? Что
обозначает выражение 4•3? Чему равно его значение?
88
847 м
13 м
140 м
1км
Океан
Корабельная
роща
Деревня
Озеро
Выбираем задания и тренируемся

34. 34
Момо рассказала несколько историй.
а) Томми и Мьямба соревновались в плавании. Они поплыли одновре-
менно от лодки к берегу озера. Томми проплыл это расстояние за
8 минут, а Мьямба за 5 минут.
Кто плыл быстрее, Томми или Мьямба? Кто проплывал за 1 минуту большее
расстояние?
б) За несколько часов Пеппи прошла по берегу океана 10 км, а Анни-
ка за это же время – 8 км.
Кто шёл быстрее, Пеппи или Анника? Кто проходил за 1 час большее
расстояние?
в) Моана и Боно соревновались в беге. Моана пробежала 80 м за
20 с, а Боно 45 м за 15 с.
Как узнать, кто бежал быстрее, Моана или Боно? У кого из них ско-
рость движения больше?
11
Кто двигался быстрее, и во сколько раз, если
а) одно и то же расстояние черепаха и змея проползли за разное
время: змея за 6 мин, а черепаха за 12 мин;
б) за одно и то же время страус пробежал 120 км, а лошадь
40 км?
22
Чему равна
а) скорость движения улитки, если она за 7 мин проползла 7 дм;
б) скорость движения Анники, если она на велосипеде за 6 мин про-
ехала 600 м;
в) скорость движения птицы, если она за 5 часов пролетела 250 км?
33
Узнаём новое
Бежит быстрее тот, кто за 1 с пробегает бо’льшее расстояние.
Говорят, что у него скорость движения больше.
Скоростью называют расстояние, пройденное за единицу времени.
Чтобы найти скорость, надо расстояние разделить на время движения.
Скорость – это величина. Скорости можно измерять и сравнивать.
Если расстояние измерено в метрах, а время движения в секун-
дах, то скорость измеряется в метрах в секунду (м/с), если рас-
стояние измерено в километрах, а время движения в часах, то ско-
рость измеряется в километрах в час (км/ч).
Найдём и сравним скорости движения Моаны и Боно.
Моана: 80:20 = 4 (м/с); Боно: 45:15 = 3 (м/с); 4 м/с > 3 м/с.
Значит, Моана бежала быстрее Боно.
Применяем новые знания
СКОРОСТЬ ДВИЖЕНИЯСКОРОСТЬ ДВИЖЕНИЯ2.58

35. Как вы думаете, в каких ещё единицах может быть измерена ско-
рость движения? Придумайте задачу, в которой надо найти скорость по
известному расстоянию и времени, и решите её.
Анника сделала рисунки. У кого на рисунках какая скорость?44
Выберите к задачам нужные уравнения и решите.
а) «Попрыгунья» прошла 240 км за 8 часов. Её скорость в 5 раз
больше, чем скорость шлюпа. Чему равна скорость шлюпа?
б) «Попрыгунья» прошла 240 км за 8 часов. Её скорость на
4 км/ч меньше, чем скорость катера. Чему равна скорость катера?
55
х•4 = 240:8
х – 4 = 240:8
х:4 = 240:8
х + 4 = 240:8
Какие из высказываний Пеппи истинные?
3 ч 40 мин = 200 мин; 5 мин 6 с > 560 с; 1 сут. 18 ч < 118 ч;
1 000 м > 1 км; 1 м2 = 1 000 дм2; 1 м3 = 1 000 дм3.
66
Проведите тот же опыт, что и в задании № 9 на стр. 27. Запи-
шите результаты в такую же таблицу. Работайте в тетради.
77
Пеппи проводила такой же опыт 10 раз. У неё получилась такая запись:
Пеппи сказала Аннике, что частота появления белой карточки при про-
ведении этих 10 опытов равнялась 7, а частота появления чёрной кар-
точки – 3. Белую карточку Пеппи доставала чаще, а чёрную реже.
Чему равна сумма частот в вашем опыте? в опыте Пеппи? в опытах
других ребят?
Общее число опытов
Сколько раз вынута
белая карточка
Сколько раз вынута чёр-
ная карточка
Общее число опытов
Сколько раз вынута
белая карточка
Сколько раз вынута чёр-
ная карточка
10 7 3
6 км/ч
600 км/ч
60 км/ч
35
Выбираем задания и тренируемся

36. Объясните смысл высказываний Пеппи:
а) плот движется по реке со скоростью 2 км/ч;
б) Анника идёт по берегу со скоростью 60 м/мин;
в) пчела летит со скоростью 6 м/с.
11
2 км
Время
Расстояние
1 с 2 с 3 с 4 с
Скорость Время Расстояние
?
Скорость Время Расстояние
?
х км
Анника составила таблицу движения пчелы. Найдите неизвестное рас-
стояние, если скорость движения пчелы постоянна и равна 6 м/с.
33
Пеппи скачет на лошади со скоростью 13 км/ч. Какое рассто-
яние она преодолеет за 5 часов?
44
Чему равна скорость движения каноэ с Моаной на борту, если за
2 мин она проплыла 140 м?
55
Вспоминаем то, что важно для урока
Знакомимся с основным вопросом урока
Как узнать расстояние, если известны скорость и время движения??!
Узнаём новое
Сформулируйте ответ на основной вопрос урока.
Если известны скорость и время движения, то можно найти расстояние.
Оно равно скорости, умноженной на время движения.
Применяем новые знания
36
Чему равна скорость плота? Сколько часов плыл плот? Какое рассто-
яние он проплыл за 1 час? 2 часа? 3 часа? за всё время движения?
На рисунке Томми единичный отрезок показывает расстояние, кото-
рое плот проходит за час. Стрелка показывает, в каком направлении
он двигался.
22
ВЗАИМОСВЯЗЬ СКОРОСТИ, ВРЕМЕНИ,ВЗАИМОСВЯЗЬ СКОРОСТИ, ВРЕМЕНИ,
РАССТОЯНИЯРАССТОЯНИЯ
2.59

37. С помощью какого из этих уравнений можно решить задачу Момо?
Пеппи, Анника, Момо и Моана нашли во время ныряния по 10 рако-
вин-жемчужниц. Несколько таких раковин они подарили маленьким весе-
лянам, и у них осталось 28 раковин. Сколько раковин-жемчужниц до-
сталось в подарок маленьким веселянам?
Выполните устные вычисления по заданным блок-схемам и таблицам.77
У Пеппи и Моаны одинаковое число жемчужин для игры в шари-
ки, а у Томми жемчужин в два раза меньше, чем у Пеппи. Всего
же у них троих 200 жемчужин. Сможет ли Томми на свои жемчу-
жины выменять у рыбаков ожерелье из акульих зубов, если за одно
ожерелье надо отдать 10 жемчужин?
88
Начало
•6
:5
+95
–109
Конец
Начало
:2
Нет
Конец
Меньше 100?
Да
–65
105 115 125 150
П.
ж.М.
Т.
130 248 314 472 504
37
Прочитайте число
Назовите результат Назовите результат
Прочитайте число
Решите уравнения с объяснением и проверкой.66
4•х = 28•10
х:4 = 10 + 28
5•х = 125:5
266:х = 100 – 93
х – 28 = 4•10
40 – х = 28
Выбираем задания и тренируемся

38. 38
Боно с палубы яхты увидел плывущую к нему акулу. Через
сколько времени акула достигнет яхты, если она плывёт со скоростью
300 м/мин и находится в 900 м от яхты?
22
Решите задачи, заполняя таблицы. Работайте в тетради.
а) Пеппи отправила на «Попрыгунью» почтового голубя с сообщением о
нападении разбойников. За 4 часа голубь пролетел 120 км. С какой ско-
ростью он летел?
11
Скорость Время Расстояние
б) «Попрыгунья» вышла из бухты Веселии со скоростью 15 км/час. На
каком расстоянии от бухты она была через 3 часа?
в) Через сколько времени «Попрыгунья» вернётся в бухту Веселии,
если сейчас она находится на расстоянии 300 км от бухты и будет
двигаться со скоростью 10 км/час?
Знакомимся с основным вопросом урока
Как связаны между собой скорость, время, расстояние??!
Узнаём новое
900 м
300 м/мин
х мин
Боно рассуждал так: я знаю, что если скорость движения умножить
на время движения, то можно найти расстояние.
Мне неизвестно время, но известны скорость и расстояние. Обозначу
неизвестную величину буквой х и получу уравнение:
300•х = 900
х = 900:300
х = 3
Ответ: 3 минуты.
Как найти время движения?
Сформулируйте ответ на основной вопрос урока.
Скорость движения принято обозначать маленькой латинской буквой
v, время движения – маленькой латинской буквой t, пройденное рас-
стояние – маленькой латинской буквой s.
ВЗАИМОСВЯЗЬ СКОРОСТИ, ВРЕМЕНИ,ВЗАИМОСВЯЗЬ СКОРОСТИ, ВРЕМЕНИ,
РАССТОЯНИЯРАССТОЯНИЯ
2.60

39. Решите задачи.
а) Разбойники Джим и Бук пробежали без остановки по 960 м каждый, убе-
гая от Пеппи. Джим был в пути 3 мин, а Бук 4 мин. Чья скорость движе-
ния была больше и на сколько?
б) Сможет ли Пеппи за 8 мин доплыть до лодки капитана Эфроима, если
лодка находится в 700 м от берега, а Пеппи плывёт со скоростью
80 м/мин?
в) Разбойники будут на борту своего корабля через 9 мин. Сможет
ли лодка капитана Эфроима добраться до корабля разбойников за это
же время, если от лодки Эфроима до корабля разбойников 400 м и
лодка движется со скоростью 40 м/мин?
33
Решите уравнения.44
х:7 = 200 – 72 a – 293 = 207:9 у•6 = 800 – 512
Вычислите.55
(816:8 + 972:9)•3 (415:5 + 837:9) – 97
948 – (459 + 489) 762:3 + 684:2
(302 + 685) – 899
364:7 + 23•6
115•6 – 110:5
700 – 69•9:3 123•6:3 – 187
У Анники светлые волосы, у Моаны чёрные, а у Пеппи рыжие.
Они одеты в чёрную, белую и оранжевую набедренные повязки. «Как
смешно, – сказала девочка в чёрной повязке, – все три повязки по-
вторяют цвет наших волос, но ни одна из нас не надела повязку цве-
та своих волос».
«Ты права», – ответила ей Анника. Какого цвета набедренная повяз-
ка была на каждой из девочек?
77
Прочитайте сначала истинные, а потом ложные высказывания. Замените
ложные высказывания на истинные.
66
5 л = 5 м3
1 км = 1 000 м
100 см2 > 1 м2
2 ч 15 мин = 215 мин
2 сут = 120 ч
2 мин 6 с = 186 с
Мы знаем, что расстояние равно скорости, умноженной на время:
s = v•t ;
скорость равна расстоянию, делённому на время: v = s:t ;
время движения равно расстоянию, делённому на скорость:
t = s:v .
Применяем новые знания
Выбираем задания и тренируемся
39

40. 40
Спишите. Выразите величины в заданных единицах измерения.11
120 с = мин
300 лет = в.
3мин 10 с = с
4 сут = ч
3 нед = сут
72 ч = сут
420 ч = мин
3 г. = мес
а)
б) 240 см = м см 1000 м = км
630 мм = дм см
Вычислите. Выразите результат
а) в дециметрах:
24 м 3 дм – 340 см + 50 дм•5;
б) в минутах:
3 мин 20 с + 4 мин 40 с;
в) в метрах кубических:
(124 л + 1000 см3)•7 + 125 дм3.
22
Решите задачи.33
а) Яхта «Попрыгунья» отправилась от Кокосовых островов к берегам
Индии. В первый день она прошла до ближайшего острова 66 км,
двигаясь со скоростью 11 км/ч, а во второй день – 90 км, двигаясь
со скоростью 10 км/ч. Сколько времени «Попрыгунья» была в пути
за эти два дня?
I день
v t s
II день
Туда
v t s
Обратно
б) От борта яхты на берег туристов доставил катер. Расстояние от
берега до борта яхты он прошёл за 2 ч со скоростью 12 км/ч.
С какой скоростью катер двигался на обратном пути, если обратно
он шёл 3 ч?
в) От порта до аэровокзала туристы ехали на автобусе 2 часа со
скоростью 65 км/ч, и им осталось ещё проехать 300 км. Какое рас-
стояние от порта до аэровокзала?
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.61

41. Расшифруйте название острова, на котором находится аэропорт, из
которого Пеппи и её друзья улетели в Швецию. Работайте в тетради.
44
(532 – 142):3
(295 + 254):9•5
О
Й
434:7•3
550:5•9
Н
Л
(800 – 68):6•2Ц(190 + 450):80Е
244 8 305 990 130 186
Анника, Пеппи и Томми прилетели в Швецию в конце декабря
високосного года. В январе следующего года было 19 пасмурных дней,
а в феврале 20. Сколько ясных дней было в январе и феврале?
55
Все дома на улице, где живут Пеппи, Томми и
Анника, имеют одинаковые участки, расположенные
друг против друга. Томми и Анника живут на чётной
стороне улицы, дом Пеппи – напротив. Номер дома
Пеппи – LXI. Какой номер у дома Анники? Каким
может быть номер дома, в котором расположена
кондитерская, если этот дом стоит рядом с домом
Пеппи? (Номера домов идут на каждой стороне улицы
по порядку.)
66
V VI
III IV
I II
Пеппи, Томми и Анника начертили фигуры.
Пеппи начертила такую фигуру:
88
Томми и Анника начертили такую фигуру:
У какой фигуры бо’льшая площадь?
Подберите по два решения каждого неравенства. (х, y – натураль-
ные числа.)
77
а) 95•x < 475 б) y + 199 < 205
41

42. 42
Пеппи устроила на свой день рождения выигрышную лотерею и
приготовила лотерейные билеты для всех жителей города. Вот номера
некоторых из них: 40, 90, 110, 160, 200, 180, 625, 431.
Выигрышные номера идут через каждые 70 номеров. Какие билеты
здесь выигрышные, если первый выигрышный номер 20? Какие ещё
номера выигрышные, если в городе 1 000 жителей?
11
Пеппи устроила катание на лошади, гоночной машине и водном глис-
сере. Томми и Анника придумали про это катание несколько задач и
записали данные в таблицу. Какие это могли быть задачи?
22
v t s
180 км/ч 2 ч
12 м/с 720 м
2 мин 1000 м
а) Мальчики устроили велогонки. Томми проехал дистанцию за
15 мин, Карл за 12 мин, а Бент за 24 мин. У кого скорость дви-
жения была больше? Сравните скорости Карла и Бента.
б) Пеппи приехала со своей виллы «Курица» в кондитерскую за леден-
цами на лошади. Четыре секунды она скакала со скоростью 12 м/с,
7 с со скоростью 10 м/с и минуту со скоростью 8 м/с. Какое
расстояние от виллы «Курица» до кондитерской?
в) Пеппи купила 8 килограммов сливочных тянучек и карамели. За
тянучки Пеппи заплатила 200 э’ре, а за карамель – 120 э’ре. Сколько
килограммов сливочных тянучек и сколько килограммов карамели купи-
ла Пеппи, если цена у этих конфет одинаковая?
33
Пеппи устроила свой первый день рождения 15 мая, а второй 29
августа того же года. Сколько дней прошло между этими днями
рождения?
44
Отгадайте слово, и вы узнаете, что Пеппи подарила на свой день
рождения Томми. Работайте в тетради.
55
(405•2 + 90):6
(800 – 732:6):2
О
М
226•2 – 149•3
198•4 – 365:5
С
П
(532:2 – 186)•9К(203•4 – 120):2А
720 150 339 719 346 5
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.62

43. Устройте соревнования на скорость: кто быстрее расставит, где
это требуется, знаки арифметических действий и скобки так, чтобы
равенства были верными. Работайте в тетради.
4 4 4 4 = 5 4 4 4 4 = 17 4 4 4 4 = 20
4 4 4 4 = 32 4 4 4 4 = 64 4 4 4 4 = 48
66
В большой коробке в 2 раза больше вафель, чем в маленькой.
Половину всех вафель из большой коробки Пеппи переложила в малень-
кую. Во сколько раз в маленькой коробке стало больше вафель, чем
в большой?
Во сколько раз в маленькой коробке стало бы меньше вафель, чем
в большой, если бы Пеппи переложила из неё половину вафель в
большую коробку?
77
В соревнованиях по подъёму тяжестей Пеппи, силач Альфред и слон
из цирка получили золотую, серебряную и бронзовую медали. Силач
Альфред получил не золотую и не серебряную медали, а слон – не золо-
тую. Кто какую медаль получил?
88
В непрозрачной коробке 3 белых, 1 чёрная и 1 синяя картонные
карточки, одинаковые на ощупь. Надо провести случайный эксперимент:
вынуть из коробки 1 карточку.
Пеппи записала несколько событий для этого эксперимента. Какие
из них возможны? невозможны? случайны?
а) Вынули белую карточку.
б) Вынули жёлтую карточку.
в) Вынули 5 белых карточек.
Все ли возможные события записала Пеппи? Какие ещё возможные
события вы можете назвать? Проведите этот случайный эксперимент и
запишите результаты в такую же таблицу. Работайте в тетради.
99
Расскажите по таблице, какое событие встречалось чаще всего? реже
всего? Чему равна сумма всех частот?
Постройте по таблице столбчатую диаграмму частот. Работайте в тетра-
ди.
Общее число опытов
Частота появления карточки
белой чёрной синей
10
белая
частота
чёрная синяя
Сравните свои результаты с результатами других ребят.
43

44. 44
Пеппи печёт булочки в соответствии с алгоритмом. Чего не
хватает в блок-схеме этого алгоритма?
11
Начало
Сделайте тесто и скатайте из него булочки
Положите булочки на противень и поставьте в печь
Ждите 15 минут
Достаньте
булочки из печи
Ждите 2 минуты
Нет Да
?
Решите только те уравнения, где последнее действие, которым нахо-
дят решение, – умножение.
22
х:2 = 300 – 190 х:2 = 300 + 190 х•2 = 300 – 190
С помощью какого из этих уравнений можно решить задачи Анни-
ки?
а) Пеппи испекла булочки с корицей и
булочки с тмином – всего 300 булочек.
Когда половину булочек с корицей съели,
осталось 190 булочек. Сколько булочек с
корицей испекла Пеппи?
б) Пеппи пригласила в магазин игрушек
половину всех детей, живущих в городе.
Триста ребят уже получили подарки и ушли
домой, а 190 ещё остались в магазине.
Сколько детей живут в одном городе с
Пеппи?
Вычислите. Выразите результат
а) в километрах: в) в метрах квадратных:
15 км – (676 м + 324 м); 409 дм2 – 450 см2•2;
б) в минутах: г) в дециметрах кубических:
(360 с + 2 ч) – 125 мин; 200 см3•3 + 100 см3•4.
Придумайте задачу к любому из этих выражений.
33
Конец
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.63

45. 45
а) Томми и Пеппи решили установить, какая из игрушек быстроход-
нее – автомобиль или катер? Они установили дистанцию в 288 м на
садовой дорожке и в канаве с водой. Автомобиль преодолел эту ди-
станцию за 4 мин, а катер за 3 мин. Скорость какой игрушки боль-
ше и на сколько?
б) Пеппи отправила свой катер в путешествие по канаве длиной 800 м.
Первые 5 мин он плыл со скоростью 100 м/мин, а затем со скоростью
50 м/мин. За сколько времени катер преодолел канаву с водой?
в) Томми и Анника одновременно выбежали из магазина игрушек и
отправились домой. Томми бежал со скоростью 240 м/мин, а Анника
со скоростью 80 м/мин. Кто оказался дома раньше? Через сколько
минут добралась до дома Анника, если Томми оказался там через 3
минуты? (Томми и Анника бежали от магазина до дома без остано-
вок.)
44
Расшифруйте название катера, который Томми подарил господину
Нильсону. В честь кого назван катер? Работайте в тетради.
55
(508 – 505)•250:5
60:15•100 – 298
Г
И
80:40•185 – 295А
192:6 + 253•3
(78:78 + 999):5
К
Н
900 – (95•6 – 305)В
635 102 791 102 200 150
Начертите и раскрасьте для катера господина Нильсона ту эмблему,
которая вам больше нравится.
В школе у Анники 400 учеников. Докажите, что хотя бы двое из
них родились в олдин день года.
66
77

46. 46
В этом числовом ряду номера домов:
XVII, XXVIII, LVI, LX, CII, CCIV, D, XIV, CCCVIII.
Выберите из него несколько чисел и составьте новый ряд так, чтобы
каждое следующее число в нём было в 2 раза больше предыдущего.
Если вы выполнили это задание, то перед вами номера тех домов,
куда мама Анники послала приглашения к чаепитию.
11
Для приготовления торта нужно взбивать крем 240 секунд и час,
чтобы сделать тесто и испечь коржи. Мама Анники делает торт уже
40 минут. Хватит ли ей времени, чтобы приготовить его до прихода
гостей, которые появятся через полчаса?
22
Гости съезжаются отовсюду. Начертите и заполните таблицу и
придумайте по ней задачи.
33
v t s
80 км/ч 5 ч
30 мин 900 м
20 м/с 120 м
а) Фру Пе’терсен и фру Се’гред живут на разных концах той ули-
цы, где стоит дом Томми и Анники. Они приглашены на чаепитие в
дом Анники. Каждая потратила на дорогу 9 мин, но фру Пе’терсен
шла со скоростью 30 м/мин, а фру Се’гред со скоростью 40 м/мин.
На каком расстоянии от дома Анники живёт каждая из них? Какое
расстояние между домами фру Пе’терсен и фру Се’гред?
б) Скорость движения Пеппи в 5 раз больше скорости движения гос-
подина Нильсона. Сколько времени нужно господину Нильсону, чтобы
пройти расстояние в 800 м от дома Пеппи до дома Томми, если
Пеппи преодолела это расстояние за 4 мин?
44
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.64

47. 47
Участок, на котором стоит вилла «Курица», имеет форму квадрата
со стороной 200 м. Он был огорожен старым забором, четверть кото-
рого Пеппи разобрала, чтобы можно было свободно ходить в гости к
Томми и Аннике. Сколько метров забора осталось?
55
Томми и Анника засадили цветами клумбу для своей мамы. Жёл-
тые цветы посадила Анника, голубые – Томми. Жёлтые цветы занима-
ют площадь 5 м2. Чему равна площадь клумбы? Чему равна её шири-
на, если длина равна 5 м?
66
Как Пеппи расставить скобки в равенствах так, чтобы они ста-
ли верными?
77
100 – 30:2 = 35
540:3 + 6 = 60
135•5 – 5 = 0
200 + 30•3:10 = 29
840:10 – 6:2 = 120
6•72 – 72:6 = 0
а) У Томми 4 свитера и трое брюк. Сколько костюмов Томми может
составить из этих вещей, если любой свитер подходит к любым брюкам?
б) У Анники 5 блузок и 4 юбки. Сколько разных костюмов может
составить из них Анника, если одна блузка по цвету не подходит к
одной юбке?
88
Положите в непрозрачную коробку 3 чёрных, 2 белых, 1 красную
и 1 синюю карточки. Проведите случайный эксперимент по выбору
наугад одной карточки 10 раз и занесите результаты в такую же таб-
лицу. Работайте в тетради.
99
Общее число опытов
Частота появления карточки
белой чёрной синей красной
10
Расскажите по таблице, какое событие встречалось чаще всего? реже
всего? Чему равна сумма всех частот?
Постройте столбчатую диаграмму частот.
Сравните свои результаты с результатами других ребят.

48. 48
Томми и Анника катались в лодке по реке, когда к одному из
её берегов подошли пятеро матросов с «Попрыгуньи», которые очень
спешили в гости к Пеппи. Лодка Томми и Анники была так мала, что
на ней могли переправиться только двое детей или только один мат-
рос. Есть ли у Томми и Анники возможность переправить всех мат-
росов на другой берег?
Томми рассуждает так: если сможет переправиться один матрос, то
таким же способом смогут переправиться и все остальные. Для этого
помоги Томми найти ответы на вопросы.
Сможет ли переправиться 1 матрос и вернуть лодку на тот берег, с
которого переправился?
Если лодка должна вернуться назад, а матрос переправиться (остаться
на другом берегу), то как лодка сможет вернуться назад? Кто должен
её пригнать?
Если в лодке может находиться только 1 матрос, то где перед нача-
лом переправы матроса должен находиться тот ребёнок, который при-
гонит лодку?
Как ребёнок, который пригонит лодку назад, мог оказаться там один,
без лодки?
11
Томми и Анника поняли, как им переправить всех матросов через
реку и переправиться самим. Они придумали алгоритм переправы и
составили его блок-схему, но забыли вписать некоторые команды. Какие?
22
Начало
Томми и Анника садятся в лодку и перегоняют её на другой берег
Анника остаётся на берегу, Томми на лодке возвращается
?
?
Нет Все матросы
переправились?
Конец
Да
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.65

49. а) Томми и Анника спустились на лодке, не работая вёслами, вниз
по течению реки на 15 км. Сколько часов они были в пути, если
скорость течения реки 3 км/ч? Какое расстояние они смогли бы прой-
ти за 6 ч? 12 ч?
б) Навстречу Томми и Аннике выбежали Пеппи и господин Нильсон.
Пеппи пробежала 500 м за 5 мин, а господин Нильсон за 10 мин.
Сколько времени потребовалось бы Пеппи, чтобы пробежать 1 км? гос-
подину Нильсону?
33
Томми и Анника делают уроки. Помогите им сравнить значения
выражений в каждом столбике.
44
76•2
76•4
152•4
А
B
128:2
128:4
64:4
375 + 186
375 + 290
298 + 186
600 – 235
575 – 235
575 – 218
Как Аннике найти площадь каждой из фигур, имеющих сторону
СК?
55
M
C
K
D
F
E
Положите в непрозрачную коробку 3 белые и 2 чёрные карточки.
Выберите наугад 2 карточки. Какие события могут произойти в этом
случайном эксперименте?
События можно назвать так:
первое – обе карточки белые;
второе – обе карточки чёрные;
третье – одна карточка белая, одна чёрная.
Проведите этот эксперимент 10 раз и найдите частоту каждого собы-
тия.
66
Общее число
экспериментов
Частота событий
первое второе третье
10
Если бы в коробке лежали 3 белые и 1 чёрная карточки, то все
эти события были бы возможны? Как вы думаете почему?
В классе, где учатся Томми и Анника, 26 учеников. Найдутся ли
хотя бы трое учеников, празднующих свой день рождения в одном и
том же месяце года?
77
49

50. 50
Анника и Томми придумали несколько задач и составили к ним
таблицы. Какие задачи в одно действие на умножение и деление мож-
но придумать по этим таблицам?
11
Скорость
v
Время
t
Расстояние
s
Длина Ширина
Площадь
прямоугольника
Масса одного
контейнера
Количество
контейнеров
Масса всех
контейнеров
Цена Количество Стоимость
Как эти величины связаны между собой?
а) У кого скорость движения была больше и во сколько раз,
если за одно и то же время черепаха проползла 5 м, а слон про-
шёл 100 м?
б) Скорость движения слона в два раза меньше скорости движения
гепарда. Они пробежали одно и то же расстояние. Кто из них за-
тратил меньше времени и во сколько раз?
в) Цена билета в цирк в три раза больше цены билета в зверинец.
За несколько билетов в цирк Томми заплатил 150 эре. Сколько денег
ему пришлось бы отдать за такое же количество билетов в зверинец?
Во сколько раз больше можно купить билетов в зверинец, чем в
цирк, если на эту покупку есть 150 эре?
г) Клетка льва и клетка тигра имеют форму параллелепипеда. У какой
клетки площадь пола больше и во сколько раз, если длина клетки
льва в 2 раза меньше длины клетки слона, а ширина их клеток оди-
наковая?
22
Решите уравнения.33
х:60 = 120:12 60:х = 120:12
С помощью какого из этих уравнений можно решить задачу Пеппи?
За 12 с голубая акула проплыла 120 м. Сколько метров она проп-
лывёт за 60 с, если будет плыть с той же скоростью?
РЕШЕНИЕ ЗАДАЧРЕШЕНИЕ ЗАДАЧ2.66

51. 51
Сравните (>, <, =). Расскажите, как изменяются каждая сум-
ма, разность, произведение и частное при изменении компонентов дей-
ствий.
44
123 + d d + 223
295 – c 400 – c
s – 342 s – 456
250:b 500:b
140•k k•280
y:15 y:30
115•2 230•4
900 – 87 913 – 100
564 + 76 560 + 80
Томми начал выполнять своё домашнее задание. Продолжите его
рассуждения.
55
320 – 180 = 340 – 200 =
560 – 470
910 – 350
170 + 240 = 200 + 210 =
530 + 390
890 + 70
Как сделать вычисления быстрее?
Найдите значения выражений удобным для вас способом.66
387 + (345 – 187)
(497 + 433) – 197
У
810 – (90 + 20)
293•2 + 107•2
(392 + 269) + 108
275•2 – 175•2
После уроков учительница Томми и Анники отправилась на прогул-
ку по лесу. Она взяла с собой пять учеников: трёх девочек и двух
мальчиков.
На берегу реки они нашли лодку, в которой могли поместиться
или двое детей, или один взрослый. Смогли ли они все переправиться
на другой берег, если девочки не умели грести?
Сколько мальчиков могут переправить на другой берег всех девочек?
Когда все девочки переправятся, то как переправиться учительнице и
двум мальчикам?
Похожа ли эта задача на задачу № 1 на стр. 48? Если похожа,
то чем?
Чтобы не запутаться в рассуждениях, обозначь учительницу буквой У, маль-
чиков: м-1, м-2; девочек: д-1, д-2, д-3.
Проведите полоску, которой обозначьте реку, стрелкой – движения лодки,
и записывайте все перемещения. Вот так:
77
1)
2)
3)
У
м-1 м-2 д-1
м-2 д-2 д-3
У м-2 д-2 д-3
д-2 д-3
м-1 д-1
м-1
д-1

52. В С
Какие фигуры начертила Анника? На какие группы их можно
разбить?
11
Измерьте и сравните стороны всех красных треугольников, синих треугольни-
ков, зелёных треугольников. Как ещё можно назвать все красные тре-
угольники? все синие треугольники? все зелёные треугольники?
Сколько фигур на чертеже Томми? Назовите сначала равносто-
ронние, а потом разносторонние треугольники.
22
А DE
52
Узнаём новое
У красных треугольников на чертеже длины всех трёх сторон равны. Их
называют равносторонними.
У синих треугольников равны длины двух сторон. Эти стороны
называются боковыми, а третья сторона – основанием треугольника.
Синие треугольники – равнобедренные.
У зелёных треугольников длины сторон разные. Это – разносто-
ронние треугольники.
Применяем новые знания
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИКИ2.67

53. 53
Чтобы найти периметр одного из этих треугольников, Томми составил
выражение: 45 мм•3. Периметр какого треугольника можно найти с
помощью этого выражения?
Назовите на этом чертеже несколько острых и несколько тупых углов.
Боковая сторона равнобедренного треугольника равна 75 мм, а
периметр равен 20 см. Найдите его основание.
33
Начертите по клеточкам такой же узор, как начертила Анника.
Раскрасьте равносторонние треугольники зелёным цветом, а равнобед-
ренные – синим.
44
а) Анника за 4 минуты раскрасила 20 треугольников, а Пеппи за
это же время раскрасила 16 таких же треугольников. Кто из них
раскрасил за одну минуту больше треугольников и на сколько? (У кого
скорость раскрашивания больше?)
б) У Томми есть 36 пятиэровых монеток, а у Анники – 18. Они
решили купить на все свои деньги рыболовную леску по одинаковой
цене. Кто из них может купить больше лески и во сколько раз?
в) Пеппи отправилась верхом на лошади за покупками в соседний город. Ей
надо проехать 39 км. Сможет ли она преодолеть это расстояние за 4 часа,
если будет скакать на лошади со скоростью 13 км/час и при этом один час
потратит на остановки?
55
Как Томми быстро найти значения выражений из домашнего задания?66
128•2 + 172•2
560:(201 – 197)•0
189:9 + 711:9
195•5 – 5•195
85•7 + 85•3
97 + 97•9
98•4 – 89•4
92•9 – 92•8
728 – 69 – 69
Томми и Пеппи подошли к реке. К берегу была привязана лодка,
на которой можно переправить лишь одного человека. Тем не менее они
переправились через реку и продолжили путешествие. Как это прои-
зошло?
77
Выбираем задания и тренируемся

54. На какие группы можно разбить треугольники на этом чертеже?11
Как ещё можно назвать все красные треугольники? все синие треуголь-
ники? все зелёные треугольники?
Томми начертил прямоугольный равнобедренный треугольник, а
Анника тупоугольный равнобедренный треугольник. Фигуру какого цвета
начертила Анника?
22
Начертите по клеточкам такую же фигуру. Дайте ей название.33
Чему равен периметр этого треугольника?
Узнаём новое
У всех красных треугольников на чертеже есть прямой угол. Такие
треугольники называются прямоугольными.
У всех синих треугольников есть тупой угол. Такие треугольники
называются тупоугольными.
У всех зелёных треугольников все углы острые. Такие треугольники
называются остроугольными.
54
Применяем новые знания
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИКИ2.68

55. 55
Решите задачи.44
а) Мама пообещала отпустить Томми и Аннику на ярмарку, если они станут
лучшими математиками в их семье. Томми и Анника каждый час решают
одинаковое количество задач. За неделю Анника решила 30 задач, а Томми
66. Оказалось, что вместе они затратили на эту работу 16 часов. Сколько
часов затратил на решение задач каждый из ребят?
б) Пеппи купила для детей города 16 рулонов билетов на аттракцио-
ны и в зверинец по одинаковой цене. За несколько рулонов билетов
в зверинец она заплатила 44 золотые монеты, а за несколько рулонов
билетов на аттракционы – 20 золотых монет. Сколько рулонов билетов
купила Пеппи на аттракционы и сколько в зверинец, если цена биле-
тов была одинаковая?
в) Из двух кусков ткани для мартышек из зверинца сшили 36 одина-
ковых костюмов. В одном куске было 30 м ткани, а в другом
42 м. Сколько костюмов сшили из каждого куска ткани?
г) У Томми и Анники одинаковая скорость движения. Томми обошёл
ярмарку несколько раз и прошёл 12 км, а Анника прошла по ярмар-
ке 9 км. Если сложить время их движения, то окажется, что вместе
они ходили по ярмарке 7 часов. Сколько времени ходил по ярмарке
каждый из ребят?
Что общего в решениях всех этих задач?
Расшифруйте слово, и вы узнаете, какое животное усмирила Пеппи
в ярмарочном зверинце. Работайте в тетради.
55
204:4 + 192•3Т
(184:8 + 177):2Ц
505 – (45•6 – 35)Р
(109 – 99)•25:5Г
69:23•100 – 98И
80:16•72 + 240А
627 202 50 270 202 100 600
Найдите число гласных букв в задании 4 (г) и заполните такую
же таблицу. Работайте в тетради.
66
Какая буква встречается чаще других? реже?
Нарисуйте столбчатую диаграмму частот появления гласных букв в
этом задании.
Всего
гласных букв а е ё и о у ы э ю я
Выбираем задания и тренируемся

56. 56
Перечислите номера треугольников, которые являются элементами
множества
а) прямоугольных треугольников; б) тупоугольных треугольников;
в) остроугольных треугольников; г) равносторонних треугольников;
д) равнобедренных треугольников.
11
Какое из высказываний Анники истинное?
а) Все розовые треугольники – разносторонние.
б) Некоторые голубые треугольники – равнобедренные.
в) Никакие зелёные треугольники – не равносторонние.
Можно ли равносторонний треугольник назвать равнобедренным?
Анника сделала рисунки некоторых множеств. Дайте название
каждому из пересечений этих множеств.
22
Какие треугольники из задания № 1 можно нарисовать на пересечении
этих множеств?
Начертите треугольник, который является элементом множества
а) прямоугольных равнобедренных треугольников;
б) тупоугольных разносторонних треугольников.
равнобедренные
треугольники ? прямоугольные
треугольники
тупоугольные
треугольники ? разносторонние
треугольники
1
7
6
3
5 8
Сколько на чертеже Томми треугольников? прямоугольников?
Запишите их названия.
33
А
D
E
C
В
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИКИ2.69
2
4

57. 57
Томми раскрасил свой чертёж. Площадь закрашенной части рав-
на 7 см2. Во сколько раз площадь всего прямоугольника больше пло-
щади закрашенной части?
44
Чему равна площадь незакрашенной части фигуры?
а) Пеппи решила устроить каток в гостиной на полу прямо-
угольной формы и вылила на него несколько вёдер воды. Длина го-
стиной 27 м, а ширина 5 м. Сколько вёдер воды она вылила, если
на каждые 3 м2 пола пришлось 2 ведра воды?
б) Для украшения своего сада Пеппи заказала в питомнике ботаниче-
ского сада 9 саженцев кокосовых и финиковых пальм по одинаковой
цене. Кокосовые пальмы стоят 72 золотые монеты, а финиковые – 90
золотых монет. Каких пальм Пеппи заказала больше и на сколько?
в) Томми отправился на велосипеде в соседний город, до которого
18 км, за саженцами и собирался потратить на дорогу туда и обрат-
но 4 ч, но в пути он смог проезжать в час на 3 км больше, чем
предполагал. На сколько часов меньше потратил Томми на дорогу, чем
собирался?
55
Как Аннике рассадить 3 куста роз на клумбах
так, чтобы в каждой клумбе было
а) по 3 куста; б) по 2 куста; в) по 1 кусту?
66
Вычислите и проверьте.77
576:8 273:3 160:4 315•3 95•4 120•5
326
807
+
5 4
12
438
–
Какие цифры должны стоять вместо « », чтобы вычисления были
верными?
88
3
7
1
6
2
36
0
–
–
Найдите число гласных букв в задании № 5 (в). Заполните таблицу,
как в задании № 6 на стр. 55. Какая буква встречается чаще других?
реже?
Нарисуйте столбчатую диаграмму частот.
Сравните результаты опытов этого и прошлого уроков. Верно ли, что
одна и та же буква встречается чаще всего? реже всего?
99

58. 58
Назовите одинаковые промежутки времени.11
48 ч 15 мин ч 1 мин. 20 с недели 1 сутки
80 с 7 мин 30 с 450 с 2 суток суток 12 ч
1
4
1
7
1
2
Выразите
а) число 534 в десятках и единицах, в сотнях и единицах;
б) 534 см в дециметрах и сантиметрах, в метрах и сантиметрах;
в) 534 мм в сантиметрах и миллиметрах, в дециметрах и милли-
метрах;
г) 534 кг в центнерах и килограммах;
д) 534 копейки в рублях и копейках.
22
Вычислите33
а) 3 м 47 см – 19 дм;
б) 316 кг + 4 ц;
в) 5 м2 – 16 дм2;
г) 600 см2 – 5 дм2 4 см2;
д) 20 км + 1000 м;
е) 200 л + 200 дм3•4.
Улитка проползла от куста роз до крыльца виллы «Курица»
9 м, проползая каждую минуту по 10 см.
Когда она начала своё движение от куста роз к крыльцу, если
приползла к первой ступеньке в 10 ч 15 мин утра?
Достаточно ли у неё времени, чтобы спрятаться от господина Ниль-
сона под пустым ведром, если до ведра 45 дм, ползти она будет с
той же скоростью, а господин Нильсон выйдет на крыльцо через
50 мин?
44
Господин Нильсон родился 12 марта, а встреча с улиткой произо-
шла 18 августа следующего (високосного) года. Сколько месяцев он
прожил до встречи с улиткой? Сколько дней?
55
Составьте с помощью таблиц задачи и найдите неизвестные
величины.
66
Скорость Время Расстояние
Одинаковая
6 ч 120 км
18 ч ? км
Цена Количество Стоимость
15 монет
Одинаковое
75 монет
? монет 150 монет
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ над ЧИСЛАМИАРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ над ЧИСЛАМИ2.70

59. 59
Количество
человек в одной
машине
Количество
машин
Количество
человек во всех
машинах
6 120
Одинаковое
? 360
Сколько способов решить эти задачи вы нашли?
Решите уравнения с объяснением и проверкой.77
60•х = 540 – 180
120:n = 20•3
y:6 = 192 – 60
789 – c = 456 + 97
Познакомьтесь со старинной задачей и постарайтесь её решить.
Может ли крестьянин перевезти через реку волка, козу и капусту,
если в лодку вместе с ним помещается только или волк, или коза,
или капуста.
(Нельзя оставить без присмотра ни волка с козой, ни козу с капус-
той.)
88
Если вы затрудняетесь решить эту задачу, то ответьте сначала на такие
вопросы:
а) кого крестьянин должен перевезти первым?
б) должен ли крестьянин перевезти волка, козу и капусту только один
раз, или он может это делать несколько раз то в одну, то в дру-
гую сторону до тех пор, пока все не переправятся?
Возьмите календарь наблюдений за природой за сентябрь, за апрель,
за ноябрь. Подсчитайте в каждом месяце число солнечных, пасмурных
дней и дней с переменной облачностью. Какие дни встречались в
каждом месяце чаще? реже?
99

60. 60
Расшифруйте слова, расположив результаты действий в порядке воз-
растания. Работайте устно.
11
:2 –20
Начало
•5
Число
чётное?
Да Нет
Конец
Начало
:4
+90
Меньше 200?
Да Нет
Конец
420 360 200 160
Ц И Л Б
х
y
120
240
130
260
140
280
150 160 170
y = x...
х
y
960
320
810
270
720
240
618 426 315
y = x...
х
y
960
800
810
650
720
560
618 524 315
y = x...
х
y
120
200
130
210
140
220
150 160 170
y = x...
12 13 14 15
Т Н У И
16
Р
17
Р
В этих таблицах записаны значения х и у. Каким арифметическим
действием из х получим соответствующие значения у? Запишите выра-
жения. Найдите недостающие значения у. Работайте устно.
22
Сравните (>, <, =). (x, у – натуральные числа.)33
х•15 (х•3)•15
х•15 х•(15:3)
х:15 х:(15:3)
х:15 х:(15•3)
х•у х•(у•5)
х•у (х:4)•у
15:у (15:3):у
15:х (15:3):х
х•у (х•2)•(у•3)
х•у (х:4)•(у:3)
45:15 (45:3):(15:3)
45:15 (45•2):(15•2)
Прочитайте число
Назовите результат
Прочитайте число
Назовите результат
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ над ЧИСЛАМИАРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ над ЧИСЛАМИ2.71

61. Найдите значения выражений. Назовите только те из них, которые
являются натуральными числами.
44
Томми и Анника делают уроки. Помогите им сравнить значения
выражений в каждой строке.
55
156•4
156 + 44
156 – 97
156:2•4
156 + 88
149 – 97
312•2
149 + 88
149 – 90
78•8
149 + 95
163 – 90
а) Томми и Анника играли в игру «Кто первый засмеётся?». Сколько
раз смеялся Томми, если он смеялся в 3 раза больше Анники, а
Анника смеялась 26 раз?
б) Пеппи играла в эту игру с Томми и Анникой 250 раз, с капита-
ном Эфроимом в два раза больше, а с господином Нильсоном на
450 раз меньше, чем с капитаном Эфроимом. Сколько раз Пеппи
играла в игру «Кто первый засмеётся?» с господином Нильсоном?
в) Пеппи и её папа подкидывали друг друга в воздух. Сколько раз
взлетела в воздух Пеппи, если она взлетела на 70 раз меньше, чем
папа, а папа взлетел в воздух 360 раз?
66
По длинной узкой канаве Томми и Пеппи запустили навстречу друг
другу по три лодки. Канава такая узкая, что две лодки в ней разъ-
ехаться не могут, но в ней есть маленький залив, в котором может
поместиться одна лодка. Могут ли лодки Томми и Пеппи разъехаться?
77
Если вы затрудняетесь решить эту задачу, то ответьте сначала на такой
вопрос: смогли бы разъехаться такие же лодки, если бы их было
только две (по одной с каждой стороны)?
Возьмите календарь наблюдений за природой за октябрь и прове-
дите такой же эксперимент, как в задании № 9 на стр. 59. Какие
дни встречались чаще? реже? Сравните результаты этих экспериментов.
Вот и закончилось последнее путешествие. Оно начиналось на страницах
22 и 23 третьей части учебника. Вернитесь к ним и решите задачи.
88
812:4 + 108•5
(441:7 + 180): 3
(999 – 999)•20:4
45:15•124 – 108
90:45•92 + 368
605 – (48•3 – 56)
61

62. Назовите числа, следующие при счёте за числами
99, 100, 209, 999.
Как получить число, следующее при счёте за числом а?
11
Назовите числа, предшествующие при счёте числам
100, 200, 310, 991, 1 000.
Как получить число, предыдущее при счёте числу а?
22
НУМЕРАЦИЯ
Запишите числа
от 80 до 101; от 790 до 810; от 592 до 580; от 1 000 до 990.
Прочитайте сначала двузначные, а потом трёхзначные числа.
Что обозначает каждая цифра в записи чисел: 592, 790, 101?
Запишите эти числа в виде суммы разрядных слагаемых, со-
ставьте с ними по две возможные суммы и две возможные разности.
33
Запишите числа в порядке убывания
3 с. 1 д. 5 ед.; 5 с. 3 ед.; 10 с.; 5 с. 3 д.; 1 с.
Расскажите, сколько здесь чисел, сколько цифр. Что обозначает
каждая цифра в записи числа?
44
Найдите закономерность и запишите пропущенные числа
а) 120, 140, 160, …, 200, …, ..., ..., ..., 300;
б) 900, 700, …;
в) 152, 160, 168, 176, …, …, …, …, 216.
55
Прочитайте сначала истинные, а потом ложные высказывания. Заме-
ните ложные высказывания на истинные.
а) 610 < 620; б) 900 = 90; в) 450 > 650; г) 678 < 675.
66
Назовите самое большое однозначное, двузначное и трёхзначное
число.
77
Назовите самое маленькое двузначное и трёхзначное число.
Назовите самое маленькое однозначное число, самое маленькое
натуральное число.
88
Найдите разность самого маленького четырёхзначного числа и 1.99
62
МАТЕРИАЛЫ для ПОВТОРЕНИЯ ИЗУЧЕННОГО в ТРЕТЬЕМ КЛАССЕМАТЕРИАЛЫ для ПОВТОРЕНИЯ ИЗУЧЕННОГО в ТРЕТЬЕМ КЛАССЕ

63. 63
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ над ЧИСЛАМИ
Сложение и вычитание
Сравните (>, <, =).11
56 + 198 198 + 56
56 + (100 + 98) (56 + 100) + 98
198 – (50 + 6 ) 198 – 50 – 6
(100 + 98) – 56 100 + (98 – 56)
a + b b + a
(a + b) + c a + (b + c)
a – (b + c) a – b – c
(a + b) – c a + (b – c)
Какие свойства сложения и вычитания вы знаете?
Вычислите наиболее удобным для вас способом.22
(340 + 60) + 456
60 + 180 + 20 + 140
(450 + 90) – 50
(290 + 170) + 10
500 – (320 + 80)
840 – 170 – 230
Прочитайте сначала истинные, а потом ложные высказывания. Заме-
ните ложные высказывания на истинные. (а – натуральное число.)
а) a + 0 = 0; в) a – 0 = a; д) a – a = 0; ж) 0 – 0 = 0;
б) 0 – a = a; г) 0 + 0 = 0; е) 0 + а = а; з) а + а = 0.
33
Составьте истинные высказывания.
а) Если из суммы вычесть одно из слагаемых, то … .
б) Если к разности прибавить вычитаемое, то … .
в) Если из уменьшаемого вычесть разность, то … .
44
Вычислите с объяснением и проверкой.55
260 + 320
193 + 4
720 + 170
а)
б)
в)
890 – 250
240 + 50
220 – 110
460 + 3
270 – 150
450 + 12
430 – 20
364 + 32
362 + 125
340 + 60
600 – 40
700 – 30
130 + 70
320 + 80
200 – 20
900 – 10
410 + 90
470 + 80
530 – 60
840 – 90
370 + 40
650 + 70
410 – 30
320 – 50
980 + 30
г) 206 + 57
984 – 265
46 + 54
342 – 207
345 – 165
180 – 87
724 – 615
79 + 48
600 – 526
413 + 257
623 + 97
397 + 218

64. Решите уравнения.66
380 + х = 720
380 + х = 260 + 460
y – 560 = 400
y – 560 = 320 + 80
900 – z = 420
900 – z = 360 + 60
610 – k = 370
610 – k = 400 – 30
Решите уравнения, не вычисляя.77
х + 150 = 150 987 – z = 987
y – 560 = 0 с + с = 0
Найдите несколько решений каждого неравенства подбором.88
а) х < 34
б) 280 + t < 315
y > 100
b + b > 120
325 – a > 197
Сравните, не вычисляя (>, <, =). На сколько каждая сумма спра-
ва больше или меньше суммы слева? На сколько каждая разность
справа больше или меньше разности слева?
99
140 + 190 200 + 190
140 + 190 140 + 130
140 + 190 200 + 130
140 + 190 100 + 290
210 – 90 200 – 90
210 – 90 210 – 100
210 – 90 260 – 90
210 – 90 260 – 40
197 + 69 = 200 + 66 = 266
239 + 173
459 + 480
500 – 199 = 501 – 200 = 301
601 – 75
315 – 285
Расскажите, как сделаны вычисления. Найдите значения остальных
выражений.
1010
Проверьте себя. Хорошо ли вы знаете таблицу сложения и вычи-
тания?
а) Суммой каких двух однозначных слагаемых можно заменить числа
от 2 до 18?
б) Можете ли вы правильно решить примеры каждого столбика за 30
секунд?
1111
Составьте несколько сумм и разностей и найдите их значения.
64

65. 3 + 4
2 + 8
4 + 6
2 + 5
3 + 6
7 + 2
5 + 5
7 + 5
8 + 6
4 + 9
5 + 6
9 + 7
3 + 8
4 + 7
10 – 2
8 – 5
7 – 3
9 – 4
10 – 6
6 – 3
5 – 2
15 – 7
18 – 9
14 – 6
11 – 2
12 – 5
13 – 7
16 – 8
9•3
6•5
8•4
9•5
7•6
4•4
7•8
4•3
5•8
3•6
7•7
5•9
28:4
15:5
36:6
56:8
64:8
35:7
27:3
81:9
12:4
42:7
32:4
9:3
Умножение и деление
Проверьте себя. Хорошо ли вы знаете таблицы умножения и деле-
ния?
а) Продолжите ряды чисел.
2, 4, 6, … 5, 10, 15, … 7, 14, 21, … 3, 6, 9, … 6, 12, 18, …
36, 32, 28, … 72, 64, 56, … 81, 72, 63, …
б) Можете ли вы правильно решить примеры каждого столбика за 30
секунд?
11
Сравните (>, <, =).22
6•108 108•6
6•108 6•100 + 6•8
198:2 100:2 + 98:2
a•b b•a
(a + b)•c a•с + b•c
(b + c):a b:a + c:a
Какие свойства умножения и деления вы знаете?
Прочитайте сначала истинные, а потом ложные высказывания. Заме-
ните ложные высказывания на истинные.
а) a•0 = 0; б) 0:a = a; в) a:a = 1; г) a•1 = 1; д) a:1 = a.
33
Решите уравнения, не вычисляя.44
х•150 = 150 987:z = 987 y:560 = 0 с•с = 0
Составьте истинные высказывания.
а) Если делитель умножить на частное, то … .
б) Если делимое разделить на частное, то … .
в) Если произведение разделить на один из множителей, то ... .
Всегда ли произведение можно разделить на один из множителей?
55
65

66. 66
Вычислите с объяснением и проверкой.66
32•3
42:3
27•4
85:5
95•7
93:3
5•19
32:4
8•25
72:6
а)
39:13
60:20
45:15
90:30
48:24
120:60
72:36
240:80
50:25
720:90
б)
200•3
140•2
170•5
90•5
480:4
406:2
600:3
306:3
315:3
600:200
304:2
420:2
450:5
8•105
840:7
450:90
210•3
320:2
в)
Выполните деление с остатком.77
15:4
18:7
56:6
35:2
44:3
63:5
40:15
82:40
65:16
Вычислите в столбик с объяснением и проверкой.
а) 241•2; 312•3; 122•2; 211•4
б) 362•2; 115•4; 131•6; 57•4; 81•2
в) 862:2; 888:4; 633:3
г) 783:3; 984:2; 655:5
д) 62•7; 361•3; 134•4; 260:4; 273:3
88
Сравните, не вычисляя (>, <, =). Во сколько раз каждое произ-
ведение справа больше или меньше произведения слева? Во сколько
раз каждое частное справа больше или меньше частного слева?
99
140•3 140•6
280•3 140•3
180•4 90•2
120:3 120:6
120:3 60:3
120:3 60:6
240:3 120:3
240:6 120:3
120•х = 240
120•х = 80•3
60•х = 240:2
х•2 = 240•2
400:y = 8
(500 – 100):y = 8
400:y = 320 – 302
z:7 = 80
z:7 = 40•2
Решите уравнения.1010
Найдите несколько решений каждого неравенства подбором.
180:t < 90 b•120 > 120 a:2 > 40
1111

67. 67
СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ И ДЕЛЕНИЕ
Расскажите, в каком порядке выполняются действия, и найдите зна-
чения выражений.
11
204:4 + 192•3
(184:8 + 177):2
505 – (45•6 – 35)
(109 – 99)•25:5
69:23•100 – 98
80:16•72 + 240
а)
(39:3 + 97)•4:2
890 – 475:5 + 205
48:24•246:4
(108 + 392) – 225:5
(765 – 279):6 + 119
52:13•100 + 67
б)
372:6 + 123•3
(245:245 + 699):5
48:12•78 – 278
502 – (95•4 – 105)
(678 – 675)•125:5
(15 + 25)•2 + 70
60:15•235 – 298
125:5 + 23•9
в)
27•3:9 + 180
16•4:2 + 254
360 – 45:15•30
600 – 12•5:6
480 + 60:15•5
710 – 48:24•40
г)
4•(450:5)•0
350•2 – 2•350
80•5 + 80•4
67•8 – 5•67
145•4 – 96•4
215•3 + 215
434:7•3
550:5•9
(190 + 450):80
(532 – 142):3
(295 + 254):9•5
(800 – 68):6•2
д)
Найдите значения выражений удобным для вас способом.22
Выполните устно вычисления по заданным блок-схемам и таблицам.33
•4 +177
Начало
:2
–60
Результат
больше 3?
Да Нет
Конец
Начало
•3
:5
Результат
меньше 75?
Да Нет
Конец
105 115 125 150 175 126 248 314 472 504
:3
Прочитайте
число
Прочитайте
число
Назовите
результат
Назовите
результат

68. 68
Найдите недостающие числа. Работайте устно.44
b
d
b•d
123
6 3
186
5
500
350
0
b
d
b:d
420
6
350
35
1
408
208
208
b
d
b+d
119
283 728
819
354
600
412
412
b
d
b–d
700
129
475
90
75
98
1 000
0
ВЕЛИЧИНЫ И ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
На какие группы можно разбить фигуры на рисунке?11
Назовите каждую фигуру на рисунке.
Найдите среди этих фигур прямоугольники и начертите такие же.
Найдите их периметры.
Назовите фигуры, которые оставили на листе такие отпечатки:
а)
б)
1
16
14
2
3
4
11
13
12
5
8
7
10
6
15 9

69. 69
Найдите с помощью отпечатков площадь поверхности прямоугольного
параллелепипеда и куба. Найдите их объём.
На какие группы можно разбить фигуры на рисунке?22
Какого цвета равнобедренный прямоугольный треугольник? равнобед-
ренный тупоугольный?
Найдите
а) равносторонний треугольник;
б) разносторонний;
в) равнобедренный остроугольный.
Начертите и раскрасьте.33
а)
б)

70. 70
Сравните площади фигур.44
Чему равна площадь незакрашенной части каждой фигуры на чертеже?55
Найдите площадь и периметр фигур на чертеже.66
Начертите окружность радиусом 2 см 5 мм. Начертите отрезок
наибольшей длины, который может поместиться внутри этой окружности.
77
Начертите луч и отрезок так, чтобы их пересечением были
а) точка; б) отрезок.
88
Начертите ломаную длиной 9 см, состоящую
а) из двух звеньев; б) из трёх звеньев.
Какую длину может иметь каждое звено ломаной? (Назовите не-
сколько вариантов ответа.)
99
На отрезке МК длиной 14 см отметили точки А и В так, что
АМ = 10 см, а ВК = 12 см. Чему равна длина отрезка АВ?
1010
а)
а)
а) б)
б)
б)

71. 71
Найдите длину неизвестного отрезка.1212
Начертите по клеточкам такие же фигуры. Какие из них пересе-
каются? не пересекаются? Закрасьте пересечения фигур.
1111
Начертите квадрат, периметр которого равен периметру прямоуголь-
ника со сторонами 6 см 5 мм и 1 см 5 мм.
1313
Сравните (>, <, =).1414
1 000 м 5 км
500 см 4 м
20 мм 2 см
5 м 3 см 503 см
4 м 40 дм
23 дм 203 см
а)
б) 3 м2 200 дм2 100 см2 1 дм2 300 см2 3 дм2
в)
г)
3 л 3 дм3
10 см3 1 дм3
1 000 см3 1 дм3
600 дм3 1 м3
5 ц 500 кг 542 кг 562 кг
а)
а)
б) г) е)
в) д)
AC
18 дм
A B ? C1
3
б)
30 мм
? мм
18 мм 20 мм
A B С D
г)
? см
5 см
15 см 18 см
A B С D
в)
? м
A B ? C
AC1
6
A
A
D
E M
N
B
C
D K
B C N P T
O L
FM K
N
a
O
O1 O1 O2
O3
5 м

72. 72
Какое время показывают часы, если сейчас первая половина суток?
вторая половина суток?
1515
Вычислите. Выразите ответ
а) в сантиметрах:
8 м 4 см – (44 дм + 260 см);
б) в центнерах:
(524 кг + 76 кг) – 3 ц;
в) в минутах:
1 сутки – 20 ч.
1616
XII I
II
III
IV
VVI
VII
VIII
IX
X
XI
XII
IV
V
VI
VII
IX
X
XI 12 1
2
3
4
567
8
9
10
11
I
II
III
XII
IV
V
VI
VII
VIII
IX
X
XI I
II
III
VIII
ЗАДАЧИ
Подберите схему к каждой задаче. Обозначьте неизвестные вели-
чины буквами, составьте уравнения и решите с их помощью задачи.
а) После того как Шарик послал в районную газету 159 фото-
графий коровы Мурки, у него осталось ещё 3 её фотографии. Сколь-
ко всего фотографий коровы Мурки было у Шарика?
б) Кот Матроскин подсчитал, что часть его запасов сгущённого
молока составляет 3 банки. Сколько банок сгущённого молока запас
Матроскин?
в) Дядя Фёдор отправил маме и папе 159 посланий. Третью часть этих
посланий составляли письма. Сколько писем отправил Дядя Фёдор папе и
маме?
г) Почтальон Печкин получил к празднику 159 посылок. Три из них он
уже открыл. Сколько посылок предстоит открыть почтальону Печкину?
11
1
159
= 3
?
а)
1
159 159
б)
3
?
д) 2 суток 1 неделя
1 год 366 суток
5 суток 120 ч
1 год 12 мес.
2 ч 180 мин
10 мин 560 с

73. 3
73
– ?
159
в)
а)
269 ? 358
800
в) 715
506
?
б)
125 97 309
?
159
г)
?1
3
Придумайте уравнение к каждой схеме. Составьте по ним задачи.22
Том Сойер написал Бекки Тэчер 150 писем по 3 страницы каждое,
а Джо Гарпер 50 таких же писем.
Что можно узнать, найдя значения таких выражений:
150 + 50; 150 – 50; 150:50; 3•150; 3•(150 + 50); 3•150 – 3•50?
33
Том, Гек, Джо и Джим играли в стеклянные шарики. За лето Том
выиграл 180 игр, Гек в два раза меньше, Джо на 60 игр меньше,
чем Гек, а Джим столько, сколько Гек и Джо вместе. Кто выиграл
больше всего игр? меньше всего? Во сколько раз больше игр выиграл
Том, чем Джо?
44
Что ещё можно узнать, пользуясь данными этой задачи?
Том, Гек и Джо провели на острове Джексона два летних месяца:
июль и август и один день в сентябре. Третью часть этого времени
они строили плот, а шестую часть оставшегося времени – исследовали
близлежащие берега Миссисипи. Сколько времени они исследовали близ-
лежащие берега Миссисипи? (Сколько это недель?)
55
е) 67
?
ж) ?
625
г) ?
104
69
д) 310
?
105

74. 74
Во дворе воскресной школы ранним сентябрьским утром стоял шум
и хохот. Там играли в салочки 129 мальчиков и в три раза меньше
девочек. Как только они увидели учителя, так тут же уселись за сто-
лы, оставив один для учителя. Сколько столов было в воскресной
школе, если за каждым столом (кроме стола для учителя) сидело
по 4 ученика?
66
Придумайте с помощью таблиц задачи и найдите неизвестные вели-
чины.
77
Скорость
v
Время
t
Расстояние
s
Том ? 4 мин 180 м
Гек 4 км/ч ? 12 км
Джо 12 м/с 6 с ?
Решал за
1 минуту
Время
(мин)
Решил
всего
Том 15 примеров 4 мин ? примеров
Гек ? примеров 2 мин 20 примеров
Джо 12 примеров ? мин 48 примеров
Цена Количество Стоимость
Стальное перо 4 цента 90 ? центов
Тетрадь ? центов 90 540 центов
Краски 10 центов ? 900 центов
Том
Гек
Джо
Объём 1 банки
с краской
3 л
? л
5 л
Число банок
5 б.
8 б.
? б.
Объём всех
банок с краской
? л
16 л
20 л
За 2 дня Фарамант украсил изумрудами 24 башни, украшая их
поровну каждый день. За сколько дней он украсит 72 башни, украшая
каждый день столько же башен (работая с той же скоростью)?
88
Две Летучие Обезьяны провели в полёте 6 часов. Одна за это
время пролетела 480 км, а другая – 960. Скорость какой обезьяны
была больше и во сколько раз?
1010
В трёх одинаковых бочонках у Гудвина хранится 123 л отменной
храбрости. Сколько таких же бочонков ему понадобится, чтобы разлить
в них 82 литра отменной храбрости?
99

75. 75
Элли купила на ярмарке 8 красных и несколько голубых воздушных
шаров по одинаковой цене. За красные шары она заплатила 16 центов.
Это треть той суммы, что она заплатила за голубые шары. Каких шаров
Элли купила больше и во сколько раз?
1111
а) Скорость движения Элли 4 км/ч, а Тотошки 2 км/ч. Кто из них
пройдёт большее расстояние за одно и то же время и во сколько
раз?
б) За красные леденцы Пеппи заплатила 8 золотых монет, а за такое
же количество зелёных леденцов – 2 золотые монеты. Цена каких
леденцов больше и во сколько раз?
1212
Денис и Мишка купили тетради по одинаковой цене. Один заплатил
66 рублей, другой – 88 рублей. Мишка купил на 11 тетрадей меньше,
чем Денис. Сколько тетрадей купил каждый мальчик?
1313
66 р. ? т.
88 р. ? т.
11 т. – ? р.
Алёнка и Павля купили фломастеры по одинаковой цене, заплатив
48 рублей и 84 рубля. Сколько фломастеров могла купить Алёнка и
сколько Павля, если известно, что один из них купил на 3 фломас-
тера больше?
1414
Денис придумал такую задачу: У Бабы-яги три друга дракона: трёх-
главый, шестиглавый и девятиглавый. На дне рождения своей подруги
они решили устроить праздничный салют и выпустили одновременно 36
языков пламени. Сколько языков пламени выпустил каждый дракон, если
все головы выпустили одинаковое количество языков пламени?
1515
Храбрый Лев пробежал от поля до дороги из жёлтого кирпича
900 м, пробегая каждую минуту по 90 м. Когда он начал своё дви-
жение от поля до дороги из жёлтого кирпича, если прибежал к доро-
ге в 6 ч 5 мин утра?
Достаточно ли у него времени, чтобы спрятаться от Летучих Обезь-
ян под большим деревом, если до него 450 м, бежать он будет с
той же скоростью, а Летучие Обезьяны появятся через четверть часа?
1616
Тотошка родился 14 сентября, а ураган унёс его в Волшебную
страну 23 августа следующего года. Сколько месяцев было Тотошке в
этот день? сколько дней?
В этой задаче есть два варианта ответа. Почему?
1717

76. 76
После уроков Томми и Анника ели мороженое. Сколько порций съел
каждый из них, если Анника съела в два раза больше порций, чем Томми,
а Томми съел на 2 порции мороженого меньше Анники?
1818
Пеппи и Анника придумывали смешные истории. Всего они обе
придумали 100 историй, причём Пеппи придумала на 26 историй боль-
ше Анники. Сколько историй придумала каждая из них?
1919
На вилле «Курица» появилось 18 котят. 14 из них с чёрной шер-
стью, а 7 с белой. Сколько среди этих котят имеют чёрные и белые
пятна?
2020
18 к.
чёрные белые
?
14 7
Пеппи составила такую задачу:
Среди моих друзей 8 умеют плавать кролем, 15 – брассом, а трое
из них умеют плавать кролем и брассом. Сколько всего моих друзей
плавают кролем и брассом?
2121
умеют плавать
кролем – 8 ч. 3 ч.
? ч.
умеют плавать
брассом – 15 ч.
Том Сойер проиграл Джо Гарперу 30 стеклянных шариков, в сле-
дующей игре он увеличил число своих шариков в 2 раза, затем сно-
ва проиграл 60 шариков, после чего снова увеличил число оставшихся
шариков в два раза. Когда он после всех игр подарил Геку Финну
90 шариков, у него осталось 70 шариков. Сколько шариков было у
Тома вначале?
2222
?
–30 •2 –60 •2 –90
70
НЕСТАНДАРТНЫЕ и ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
а) Положите 12 палочек так, чтобы получились четыре маленьких
квадрата и один большой.
б) Из 10 палочек составьте три квадрата.
в) Превратите неверные равенства в верные, перекладывая
одну палочку; две палочки.
11

77. 77
Как разрезать каждую из фигур на две равные части? (Резать
можно только по сторонам клеточек.) Попробуйте найти несколько
способов.
22
Найдите числа, которые спрятались за геометрическими фигурами.33
8 = • •
8 = •
16 = •
24 = • • •
24 = • •
? ? ?
+ = 300
– = 146
:2 = 32
? ? ?
Спишите. Поставьте вместо « » пропущенные цифры.44
6
455
4
2 2
68
5 4
921
400
–
17
3 4
02
+
6 3
23
429
–
5
2 8
102
–
8
3
48
0
–
–
– = 4 9• = 57
Расшифруйте ребусы: ААА•2 = 8ББ
2АА•4 = БББ
ААА•А = БББ
Заполните магические квадраты, если задана сумма чисел в каждой
строке, каждом столбце и с угла на угол. Работайте в тетради.
600 390
55
170
200
210
120
140 90
Постарайтесь найти несколько способов.

78. Наберите множителями, взяв в каждой строке по одному числу.66
6 8 12
2 4 3 72
3 5 2
10 7 5
3 2 6 60
4 2 3
Пройдите лабиринты.77
а) В центре лабиринта записано
произведение чисел в воротах:
б) В центре лабиринта записан
результат таких действий:
4
2
32
4
16
2
64
1
• • : :
4
8
4
56 60
3
2 7
3 8
2
24 32
1 5
Спишите. Расставьте, где это требуется, знаки арифметических дей-
ствий и скобки, чтобы получились верные равенства.
88
9 9 9 9 = 7
9 9 9 9 = 19
9 9 9 9 = 12
9 9 9 9 = 63
9 9 9 9 = 17
9 9 9 9 = 99
В семье пять братьев. У каждого по две сестры. Сколько всего
детей в семье?
99
В стране Веселии у капитана Эфроима было три попугая: Альфред,
Боб и Стив. Один из попугаев всегда говорил правду, другой всегда
лгал, а третий иногда говорил правду, иногда лгал. Когда Пеппи зна-
комилась с попугаями, она спросила «Кто ты?» Альфред ответил: «Я
лжец». Боб: «Я хитрец: иногда лгу, иногда говорю правду!» Стив:
«Абсолютно честный попугай!»
Кто из попугаев лжец, а кто хитрец?
1010
У Анники есть две соломенные шляпы – с белой и с голубой
лентой; два платья – белое и голубое; три пары обуви: сандалии,
туфли, ботинки. Сколько различных комплектов одежды она может со-
ставить?
1111
У Дениса имеются только два ведра – одно объёмом 4 л, другое
9 л. Можно ли с их помощью набрать из реки ровно 6 литров воды?
1212
Найдите в каждом задании несколько способов.
Найдите, где можете, несколько способов.
78

79. На вопрос, кто из богатырей убил Змея Горыныча, они ответили:
Илья Муромец: – Змея убил Добрыня Никитич.
Добрыня Никитич: – Змея убил Алёша Попович.
Алёша Попович: – Змея убил я.
Известно, что только один богатырь сказал правду, а двое слукавили.
Кто убил Змея Горыныча?
1313
Том Сойер, Гек Финн, Джо Гарпер, Бекки Тэчер и Тим Бартон
бегали наперегонки. Скорость движения Тима больше скорости Гека,
скорость Джо больше скорости Бекки, но меньше скорости Гека, а
скорость Тома больше скорости Тима. Кто из ребят бегает быстрее
всех? медленнее всех?
1414
В шкафу висят 5 свитеров и 4 юбки. Сколько разных комплектов мож-
но из них составить, если один свитер по цвету не подходит
а) к одной юбке; б) ни к одной юбке?
1515
Сколько есть способов выбрать два предмета из трёх? из четырёх?
из пяти?
1616
Сколько разных трёхзначных чисел можно составить из цифр
а) 5, 9, 2; б) 5, 9, 0, если цифры в записи числа не могут
повторяться? А если могут повторяться?
1717
Дядя Фёдор задумал двузначное число, прибавил к нему 250, отнял
170 и прибавил 20. В полученном числе он зачеркнул первую цифру.
Какое число у него получилось? Почему?
Придумайте похожий фокус и покажите своим друзьям.
1818
Денис задумал однозначное число, приписал к нему справа два
нуля, прибавил задуманное число и результат разделил на задуманное
число. Сколько у него получилось? Почему?
1919
Можно ли сделать эти рисунки одним движением руки, не обводя
ни одной линии дважды?
2020
Из 101 одинакового по виду кольца одно кольцо (мы не знаем,
какое именно) по весу отличается от остальных. Можно ли за два
взвешивания на чашечных весах определить, легче или тяжелее это
кольцо, чем остальные? Находить кольцо не надо.
2121
В лодке, вмещающей только двух человек, через реку должны
переправиться три девочки и три мальчика. Девочки не хотят оставать-
ся на каком-нибудь берегу реки или в лодке в меньшинстве. Только
один мальчик и одна девочка умеют грести. Помогите им переправить-
ся.
2222
а) б)
79

80. 80
Любителям математики
Расшифруйте ребусы. (Одинаковые буквы обозначают одинаковые
цифры, а разные буквы – разные цифры.)
11
ААА•А = ААА ААА•3 = ББ6
Ребята нашли чугунный котелок, кувшин и несколько медалей. Мас-
са чугунного котелка больше массы кувшина в 5 раз, масса кувшина
больше массы медалей в 4 раза. Чугунный котелок, кувшин и медали
имеют общую массу 50 кг. Какая масса у кувшина?
22
Чему равна площадь каждого из этих отпечатков (в клеточках)?33
Найдите 99 натуральных чисел (не обязательно различных), сумма
которых равна их произведению.
44
17 веселя’н сели в две лодки и решили переправиться на другой
остров. Когда в одну из лодок сели ещё 3 человека, в ней стало
столько же веселян, сколько во второй. Сколько веселян было в каж-
дой лодке сначала?
55
Как решить задачу № 8 на стр. 15 без врытой у ручья бочки?66
Двое игроков красят по очереди полоску бумаги размером 1 х 100
клеточек. Первый за свой ход может выкрасить любые две идущие
подряд незакрашенные клеточки, а второй – три. Тот, кто не может
сделать очередной ход, проигрывает. Как должен играть первый
игрок, чтобы выиграть?
77
а) б) в)

81. СОДЕРЖАНИЕ
2.43–2.46 Умножение трёхзначных чисел в столбик....................2–9
2.47–2.49 Деление трёхзначных чисел
на однозначное число............................................10–15
2.50–2.51 Умножение и деление чисел ..................................16–19
2.52 Решение задач......................................................20–21
Путешествие 6. Последний звонок и летние каникулы ......................22–23
2.53 Запись чисел римскими цифрами ............................24–25
2.54–2.55 Календарь.............................................................26–29
2.56 Единицы измерения времени. Век ...........................30–31
2.57 Единицы измерения длины. Километр.......................32–33
2.58 Скорость движения................................................34–35
2.59–2.60 Взаимосвязь скорости, времени, расстояния ..............36–39
2.61–2.66 Решение задач......................................................40–51
2.67–2.69 Треугольники.........................................................52–57
2.70–2.71 Арифметические действия над числами ....................58–61
Материалы для повторения изученного
в третьем классе ..................................................62–79
Любителям математики .............................................. 80
Демидова Тамара Евгеньевна, Козлова Светлана Александровна,
Тонких Александр Павлович
МАТЕМАТИКА
3 класс
В 3 частях. Часть 3
Концепция оформления и художественное редактирование – Е.Д. Ковалевская
Художник – П.А. Северцов
Подписано в печать 00.00.16. Формат 84х108/16. Печать офсетная. Бумага офсетная.
Гарнитура Журнальная. Объём 5 п.л. Тираж 00 000 экз. Заказ №
Общероссийский классификатор продукции ОК-005-93, том 2; 953005 – литература учебная
Издательство «Баласс». 109147 Москва, Марксистская ул., д. 5, стр. 1
Почтовый адрес: 111123 Москва, а/я 2, «Баласс»
Телефоны для справок: (495) 368-70-54, 672-23-12, 672-23-34
http://www.school2100.ru E-mail: izd@balass.su
Отпечатано в филиале «Смоленский полиграфический комбинат»
ОАО «Издательство "Высшая школа"»
214020 Смоленск, ул. Смольянинова, 1

82. УДК 373.167.1:51+51(075.2)
ББК 22.1я71
Д30
ISBN 978-5-85939-585-9
© Демидова Т.Е., Козлова С.А., Тонких А.П.,
2005, 2007, 2011
© ООО «Баласс», 2005, 2007, 2011
Д30
Демидова, Т.Е.
Математика. 3 кл. : учеб. для организаций, осуществляющих образовательную
деятельность. В 3 ч. Ч. 3 / Т.Е. Демидова, С.А. Козлова, А.П. Тонких. – Изд. 3-е,
испр. – М. : Баласс, 2016. – 80 с. : ил. (Образовательная система «Школа 2100»).
ISBN 978-5-85939-585-9
Данное издание является учебником, поэтому не предназначено для письменного выполнения
заданий непосредственно на его страницах.
Учебник «Математика» для 3 класса соответствует Федеральному государственному образова-
тельному стандарту начального общего образования. Является продолжением непрерывного курса
математики тех же авторов и составной частью комплекта учебников развивающей Образователь-
ной системы «Школа 2100». В нём впервые в начальной школе рассматриваются элементы стохасти-
ки и способы решения некоторых занимательных и нестандартных задач.
Учебник ориентирован на развитие мышления, творческих способностей ребёнка, его интереса
к математике, функциональной грамотности, вычислительных навыков. Он является основой курса
«Математика» и составной частью курса «Математика и информатика», созданных в соответствии с
требованиями Федерального государственного образовательного стандарта начального общего
образования.
Может использоваться как учебное пособие.
УДК 373.167.1:51+51(075.2)
ББК 22.1я71
Федеральный государственный образовательный стандарт
Образовательная система «Школа 2100»
На учебник получены положительные заключения по результатам
научной экспертизы (заключение РАН от 01.11.2010 № 10106-5215/529),
педагогической экспертизы (заключение РАН от 17.01.2014 № 000360)
и общественной экспертизы (заключение НП «Лига образования» от 30.01.2014 № 138)
Руководитель издательской программы –
чл.-корр. РАО, доктор пед. наук, проф. Р.Н. Бунеев
В подготовке учебника принимали участие авторы Образовательной системы «Школа 2100»
Р.Н. Бунеев, Е.В. Бунеева, А.А. Вахрушев, Д.Д. Данилов, А.В. Горячев, О.В. Пронина
Авторы выражают благодарность А.Г. Рубину за участие в доработке учебника
Данный учебник в целом и никакая его часть не могут быть скопированы
без разрешения владельца авторских прав