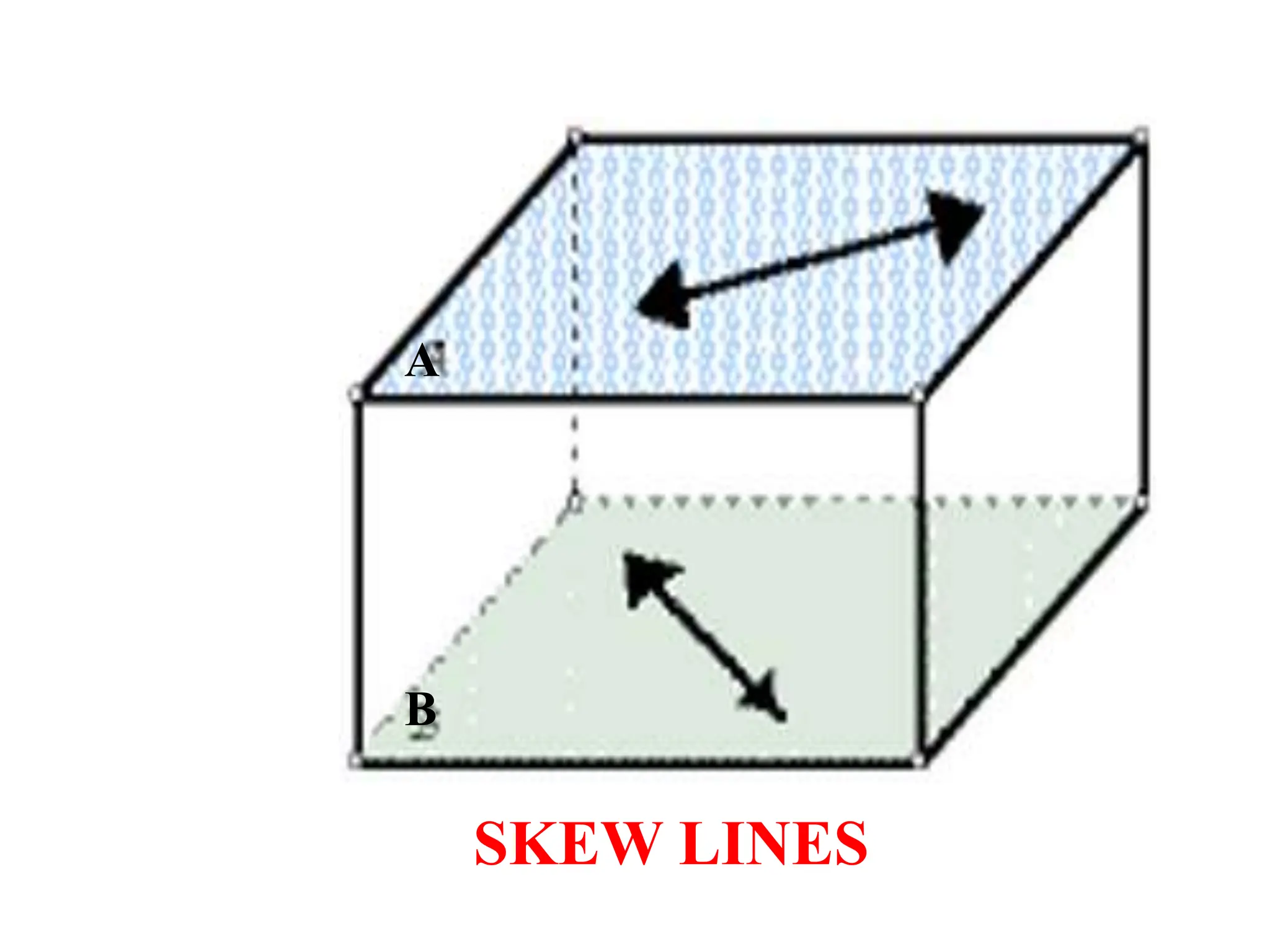
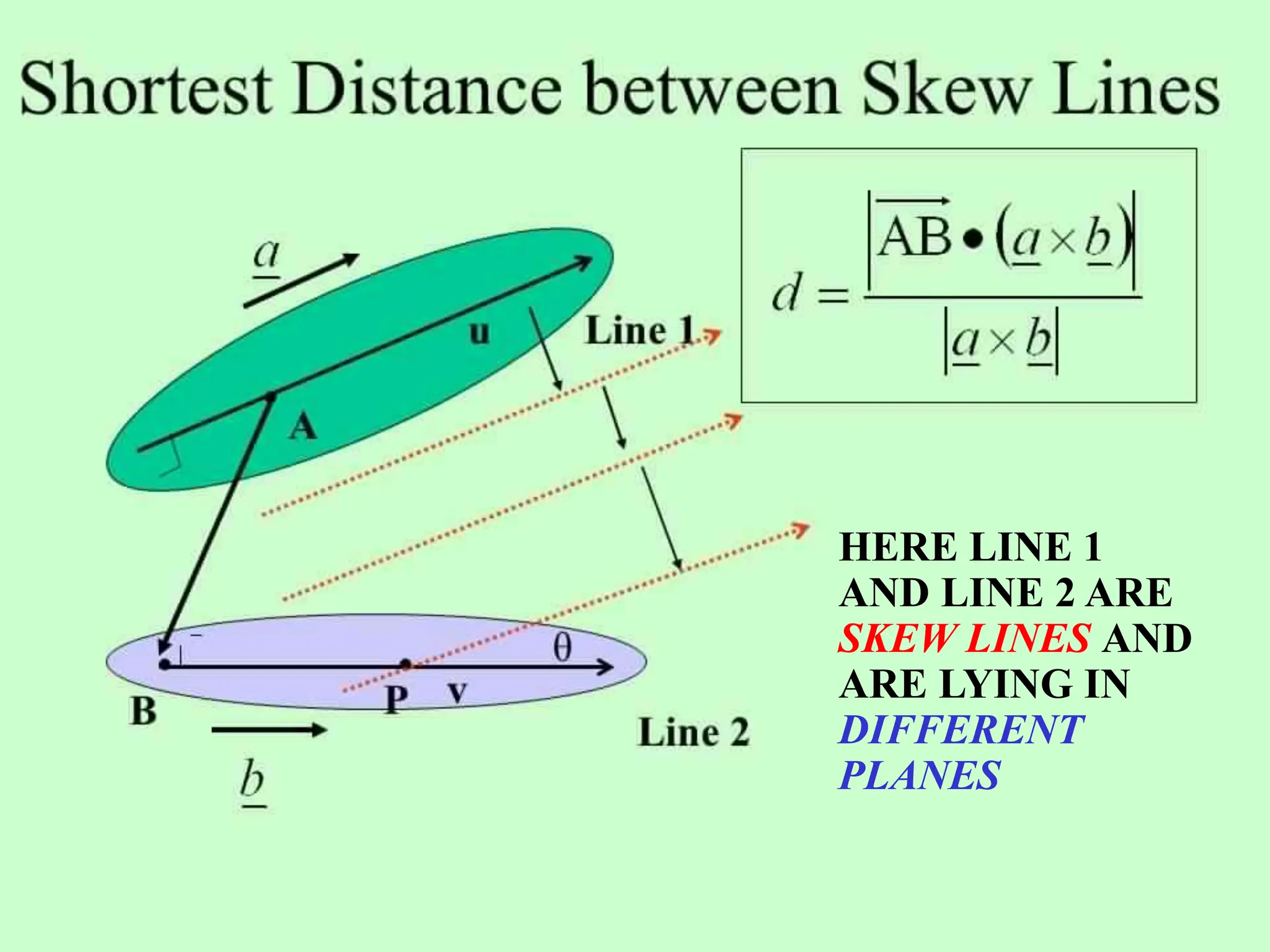
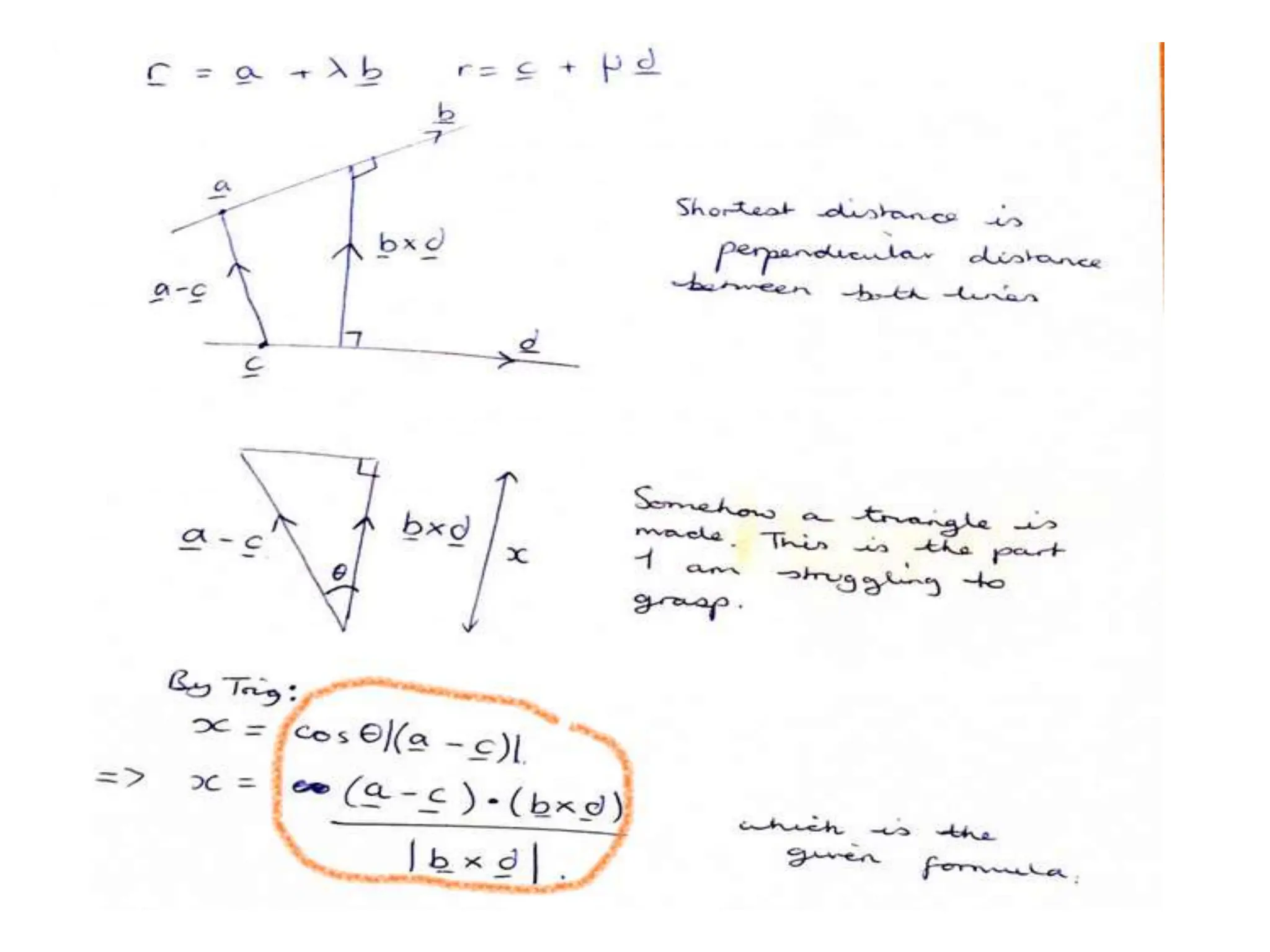
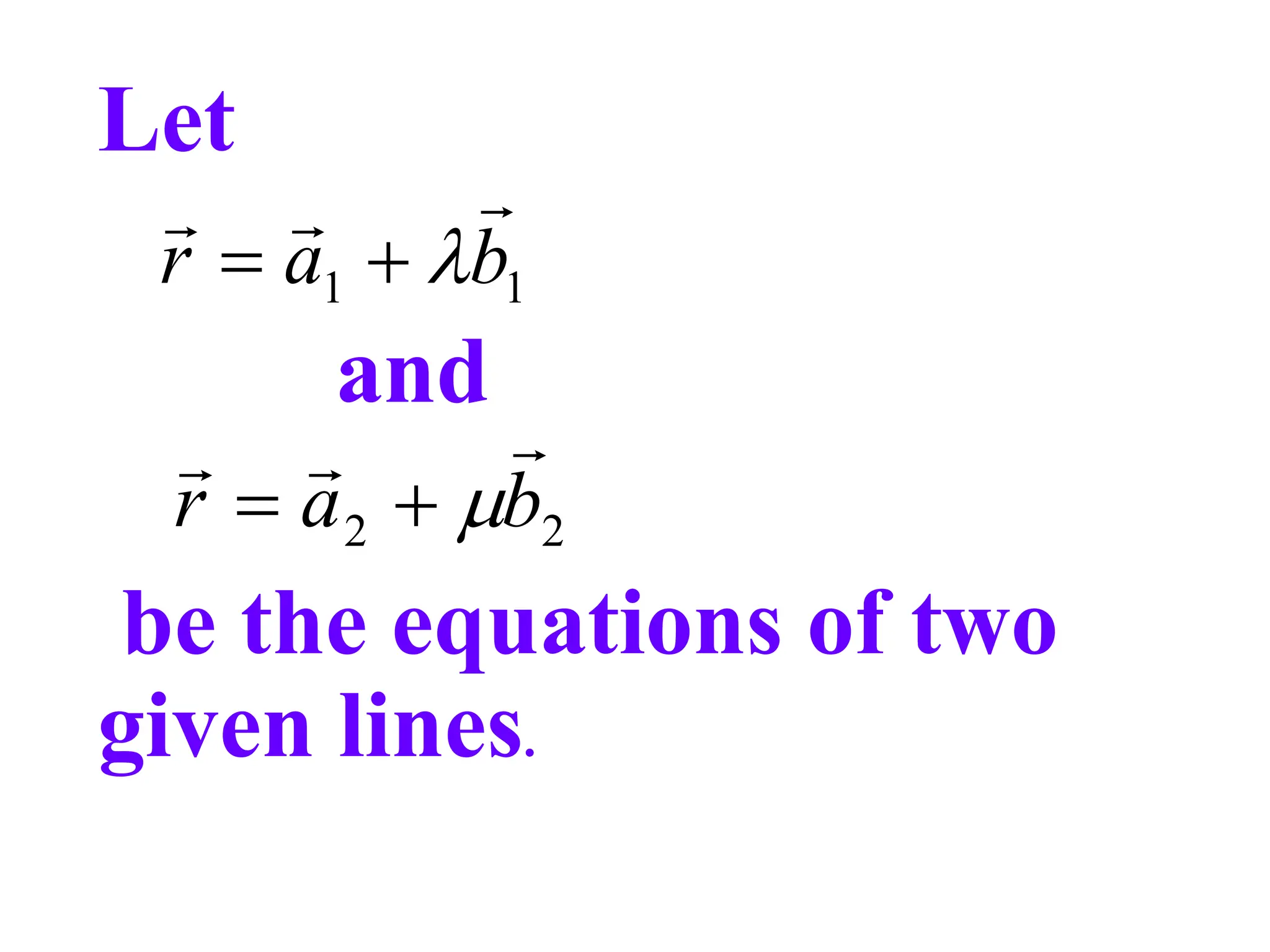This document discusses skew lines and finding the shortest distance between them. It defines skew lines as two lines that neither intersect nor are parallel. It then provides the formula to calculate the shortest distance between two skew lines given their vector equations. The formula takes the dot product of the direction vectors of the two lines and divides it by the cross product of the direction vectors. Several example problems are given to practice applying this formula to find the shortest distance between skew lines defined by different vector equations.

1. Mathematics –Class XII
Unit IV-Vector & 3D
Chapter 11 -Three
Dimensional Geometry
Sub topic-Skew lines &Shortest distance

2. LINES
• Skew lines and its Definition.
• Shortest distance and its Definition.
• Shortest distance between two skew
lines.
• Assignment
Outline:

3. SKEW LINES
B
A

4. SKEW LINES and THE
SHORTEST DISTANCE
•Two lines neither
intersecting nor parallel
are called ”Skew
Lines”.
• .
CONTINUE

5. The shortest
distance between two skew
lines is perpendicular length
between them.

6. Let
and
be the equations of two
given lines.
1
1 b
a
r






2
2 b
a
r







7. Let ‘d’ be the
shortest distance
between the
given two skew
lines, then.

8. CONTINUED
( a2 – a1 ) . b1 x b2
• d = -----------------------
| b1 x b2 |
which the shortest distance
between the given two skew lines.
BACK

9. HERE LINE 1
AND LINE 2 ARE
SKEW LINES AND
ARE LYING IN
DIFFERENT
PLANES

11. Q1.. Find the shortest distance between the
two lines whose vector equations are
• = ( i+2j +3k ) + λ ( i -3j +2k )
and
• = (4i +5j+ 6k ) -µ (2i +3j +k)
• Q2.Find the shortest distance between the
two lines whose vector equations are
• = i(1+2λ) +j(1-λ )+λ k
• =i(2+3 µ)+j(1-5 µ)+(-1+2 µ)k
r

r

ASSIGNMENT
r

r


12. • Q3.Two bikers are running at the speed more than
allowed on the road along the lines,
• = -5i -3j +6 k + t(i + 4 j --9k)
• and
• = 2i - j + k + µ(2i + j + 2k). Using shortest-
distance formula check whether they meet to an
accident or not ?
r

r

r
