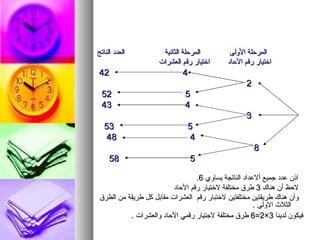
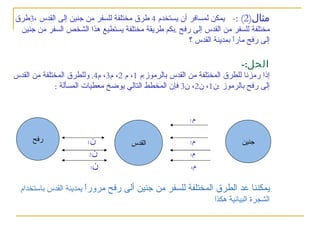
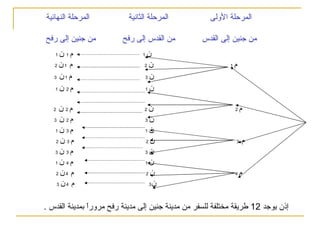
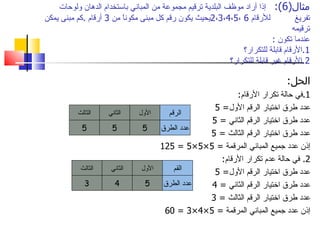
يتناول النص مبدأ العد الأساسي في الرياضيات، مع تقديم أمثلة عملية لحساب عدد الطرق المختلفة لترتيب العناصر أو الاختيار من بينها. يشرح كيفية استخدام شجرة القرار لحساب الاحتمالات، ويعرض تطبيقات في سياقات متنوعة مثل السفر والوجبات الغذائية. كما يوضح كيفية حساب عدد الطرق لاختيار المناصب المختلفة في مجلس بلدي وعدد الطرق للإجابة على أسئلة متعددة الخيارات.

2. ‫مبدأ العد ألساسي‬
‫عمل الطالبة:-فتحيه نائل طيراوي‬
‫المدرسه:-جمال عبد الناصر‬
‫الصف:-اول ثانوي تجاري”أ”‬

3. ‫الع ّ من المهارات ألساسية في الرياضيات ،فكثيرً ما تواجهنا مسائل يتطلب حلها إجراء‬
‫ا‬ ‫د‬
‫عملية ع ٍ بطريقة أو بأخرى ،ومن ذلك مث ً معرفة عدد طرق ترتيب أربعة كتب مختلفة‬
‫ل‬ ‫د‬
‫على رف ، او معرفة عدد طرق تكوين فريق لكرة السلة مكون من خمسة لعبين يختارون‬
‫من بين اثني عشر لعبا ً، أو معرفة عدد طرق اختيار كرتين من صندوق به عشرة كرات‬
‫ً‬
‫متماثلة أو.........إلخ.‬
‫للجابة عن هذه المسائل وغيرها سنتعرف على استراتيجيات مختلفة للعد ل تستخدم‬
‫اسلوب العدد المباشر وسنبدأ أو ً بالتعرف على ما يسمى بمبدأ العد ألساسي .‬
‫ل‬
‫مثال)1(: كم عددً مكونً من منزلتين يمكن تكوينه بحيث نختار رقم الحاد من بين عناصر‬
‫ا‬ ‫ا‬
‫مجموعة }82{ ،3،ورقم العشرات من بين عناصر المجموعة }54{ ،؟‬
‫الحل:-‬
‫يمكن استخدام الشجرة البيانية ل إحصاء فعلي لجميع العداد الممكنة هكذا :‬

4. ‫العدد الناتج‬ ‫المرحلة الثانية‬ ‫المرحلة الولى‬
‫اختيار رقم العشرات‬ ‫اختيار رقم الحاد‬
‫24‬ ‫4‬
‫2‬
‫25‬ ‫5‬
‫34‬ ‫4‬
‫3‬
‫35‬ ‫5‬
‫84‬ ‫4‬
‫8‬
‫85‬ ‫5‬
‫اذن عدد جميع ألعداد الناتجة يساوي 6.‬
‫لحظ أن هناك 3 طرق مختلفة لختيار رقم الحاد‬
‫وأن هناك طريقتين مختلفتين لختبار رقم العشرات مقابل كل طريقة من الطرق‬
‫الثلث الولى .‬
‫فيكون لدينا 3×2=6 طرق مختلفة لجتيار رقمي الحاد والعشرات .‬

5. ‫مثال)2( :- يمكن لمسافر أن يستخدم 4 طرق مختلفة للسفر من جنين إلى القدس ،3طرق‬
‫مختلفة للسفر من القدس إلى رفح .بكم طريقة مختلفة يستطيع هذا الشخص السفر من جنين‬
‫إلى رفح مارً بمدينة القدس ؟‬
‫ا‬
‫الحل:-‬
‫إذا رمزنا للطرق المختلفة من القدس بالرموز:م 1، م 2، م3، م4. وللطرق المختلفة من القدس‬
‫إلى رفح بالرموز :ن1، ن2، ن3 فإن المخطط التالي يوضخ معطيات المسألة :‬
‫1‬ ‫م‬
‫رفح‬ ‫ن‬
‫1‬ ‫القدس‬ ‫2‬‫م‬ ‫جنين‬
‫ن2‬ ‫م3‬
‫ن3‬ ‫م4‬
‫يمكننا عد الطرق المختلفة للسفر من جنين ألى رفح مرورً يمدينة القدس باستخدام‬
‫ا‬
‫الشجرة البيانية هكذا‬

6. ‫المرحلة النهائية‬ ‫المرحلة الثانية‬ ‫المرحلة الولى‬
‫من جنين إلى رفح‬ ‫من القدس إلى رفح‬ ‫من جنين إلى القدس‬
‫1‬ ‫م1 ن‬ ‫1‬‫ن‬
‫م 1ن2‬ ‫ن2‬ ‫1‬ ‫م‬
‫م1ن 3‬ ‫ن3‬
‫م2 ن1‬ ‫ن1‬
‫2‬ ‫م2 ن‬ ‫2‬‫ن‬ ‫2‬ ‫م‬
‫م2 ن 3‬ ‫ن3‬
‫م3 ن1‬ ‫ن1‬
‫م3 ن2‬ ‫ن2‬ ‫3‬ ‫م‬
‫م3 ن3‬ ‫ن3‬
‫م4 ن1‬ ‫ن1‬
‫م 4ن2‬ ‫ن2‬ ‫4‬ ‫م‬
‫م 4ن3‬ ‫ن3‬
‫إذن يوجد 21 طريقة مختلفة للسفر من مدينة جنين إلى مدينة رفح مرورً بمدينة القدس .‬
‫ا‬

7. ‫لحظ أن هناك 4طرق مختلفة للنتقال من جنين ألى القدس .‬
‫وأن هناك 3 طرق مختلفة للنتقال من القدس إلى رفح مقابل كل طريقة م ٍ الطرق الربعة الولى .‬
‫ن‬
‫ولذا يكون لدينا 4×3 =21 طريقة مختلفة للسفر من جنين إلى رفح مرورً بمدينة القدس.‬
‫ا‬
‫:يوضح المثالن السابقان المبدأ الساسي للعد و الذي يمكن صياغته كما يلي‬
‫مبدأ العد الساسي :‬
‫إذا أمكن إجراء عملية ما على مرحلتين ، وكان عدد طرق أجراء المرحلة الولى هو )م( وعدد‬
‫طرق إجراء المرحلة الثانية هو )ن( ، فإن عدد طرق إجراء العملية بالمرحلتين معً هو م×ن‬
‫ا‬
‫. ويمكن تعميم المبدأ السابق لكثر من مرحلتين‬
‫يقدم أحد المطاعم 4 أصناف من الحوم /و3 أصناف من السلطات وصنفين من‬ ‫مثال )3(:‬
‫. الحلوى‬
‫كم عدد الختيارات الممكنة لوجبة غذائية مكونة من صنف واحد من كل نوع ؟‬
‫:الحل‬
‫:بتم اختيار الوجبة الغدائية على ثلث مراحل‬‫1‬
‫2‬
‫. اختيار صنف من اللحوم ويتم ذلك ِ 4 طرق‬
‫ب‬
‫3‬
‫.اختيار صنف من السلطات ويتم ذلك ِ 3 طرق‬
‫ب‬
‫.اختيار صنف من الحلوى ويتم ذلك بطريقتين‬
‫أذن عدد طرق اختيار الوجبة الغدائية المكونة من صنف واح ٍ من كل نوع يساوي‬
‫د‬
‫4×3×2=42طريقة‬

8. ‫مثال )4(: بكم طريقة يمكن أن نختار رئيسً ونائبً للرئيس وسكرتيرً لمجلس بلدي‬
‫ا‬ ‫ا‬ ‫ا‬
‫مكون من 9 لعضاء ، بحيث ل يشغل العضو الواحد مركزين مختلفين ؟‬
‫الحل:‬
‫الرئيس نائب الرئيس السكرتير‬ ‫المركز‬ ‫يمكن اشغال مركز الرئيس ِ9 طرق .‬
‫ب‬
‫7‬ ‫8‬ ‫9‬ ‫عدد الطرق‬ ‫يمكن اشغال مركز نائب الرئيس ِ8 طرق .‬
‫ب‬
‫يمكن اشغال مركز نائب الرئيس ِ7 طرق .‬
‫ب‬
‫فإن يمكن اسغال المراكز اُلث ِ 9×8×7=405 طرق.‬
‫ب‬ ‫ل‬
‫مثال )5(:‬
‫تقدم شخص لمتحان مكون من 5 أسئلة من نوع الصواب )ص(والخطأ)خ(،فإن أجاب الشخص‬
‫عن السئلة جميعها يصورة عشوائية،يمكن أن تظهر إجابات هذا الشخص ؟ اكتب 4طرق‬
‫مختلفة من هذه الطرق.‬
‫الحل:‬
‫يمكن للشخص أن يجيب عن السؤال الول يطريقتين )إما صواب أو خطأ( ،كما يمكن له أن‬
‫يجيب عن السؤال الثاني بطريقتين )إما صواب أو خطأ(وهكذا..... حتى السؤال الخامس.‬
‫إذن عدد الطرق الجابة عن جميع السئلة=2×2×2×2×2=23طريقة.‬
‫ومن هذه الطرق : )1( ص ص خ ص خ‬
‫)2( ص خ ص ص ص‬
‫)3(خ خ خ خ خ‬
‫)4(ص ص ص خ خ‬

9. ‫مثال)6(: إذا أراد موظف البلدية ترقيم مجموعة من المباني باستخدام الدهان ولوحات‬
‫للرقام 6 ،5،4،3،2يحيث يكون رقم كل مبنى مكونً من 3 أرقام .كم مبنى يمكن‬
‫ا‬ ‫تفريغ‬
‫ترقيمه‬
‫عندما تكون :‬
‫1.الرقام قابلة للتكرار؟‬
‫2.الرقام غير قابلة للتكرار؟‬
‫الحل:‬
‫1.في حالة تكرار الرقام:‬
‫عدد طرق اختيار الرقم الول= 5‬
‫الثالث‬ ‫الثاني‬ ‫الول‬ ‫الرقم‬
‫عدد طرق اختيار الرقم الثاني = 5‬
‫5‬ ‫5‬ ‫5‬ ‫عدد الطرق‬
‫عدد طرق اختيار الرقم الثالث = 5‬
‫إذن عدد جميع المباني المرقمة = 5×5×5 = 521‬
‫2. في حالة عدم تكرار الرقام:‬
‫الثالث‬ ‫الثاني‬ ‫الول‬ ‫القم‬ ‫عدد طرق اختيار الرقم الول= 5‬
‫3‬ ‫4‬ ‫5‬ ‫عدد الطرق‬ ‫عدد طرق اختيار الرقم الثاني = 4‬
‫عدد طرق اختيار الرقم الثالث = 3‬
‫إذن عدد جميع المباني المرقمة = 5×4×3 = 06‬