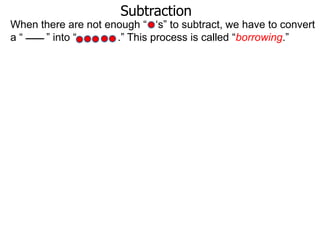
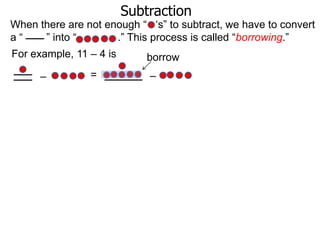
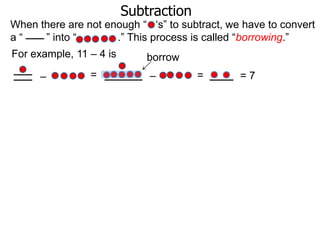
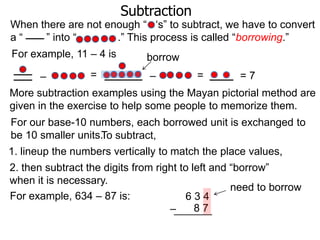
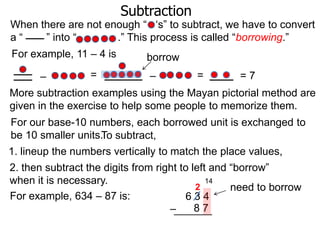
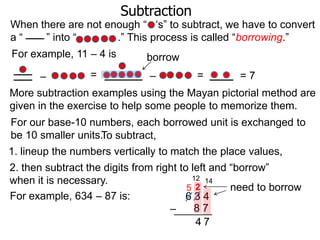
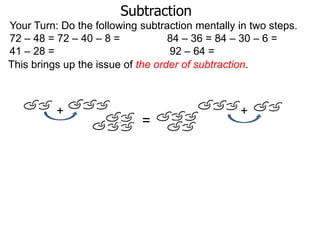
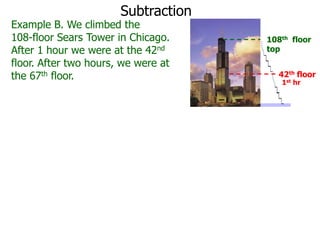
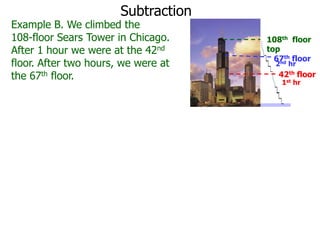
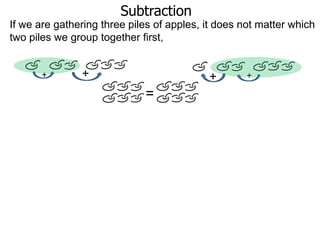
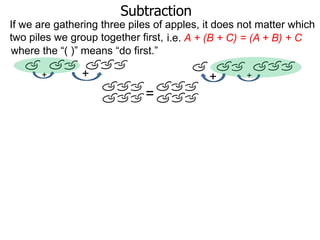
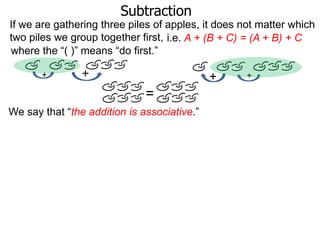
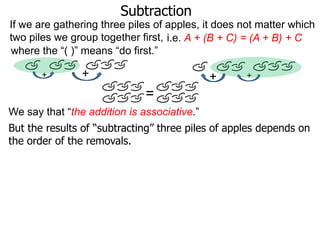
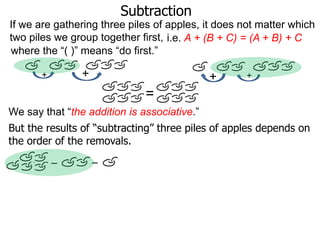
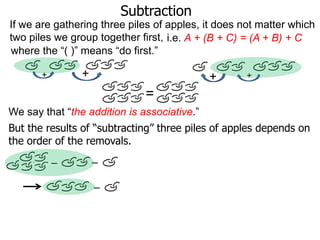
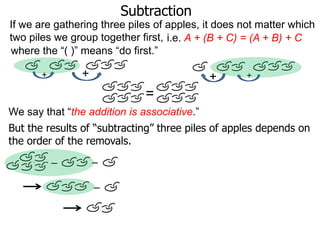
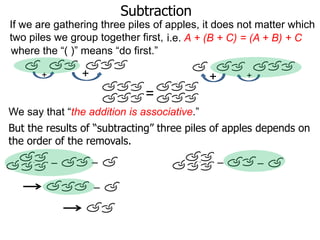
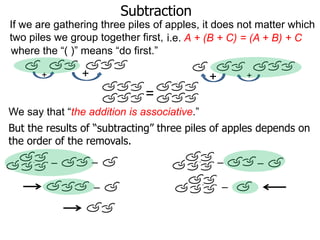
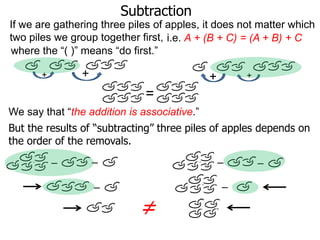
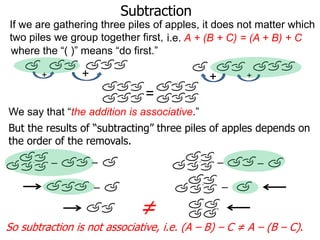
The document discusses subtraction. It defines subtraction as taking away or undoing addition. It explains that subtraction is written as A - B, where B is taken away from A. The outcome is called the difference. Subtraction can be done by lining numbers vertically and subtracting digits from right to left, borrowing from the left when needed. Mayan numerals provide a visual way to subtract small numbers. Practicing subtracting multiples of 10 and single digits from two-digit numbers helps become comfortable with subtracting two-digit numbers.

1. Subtraction
http://www.lahc.edu/math/frankma.htm

2. Subtraction
To subtract is to take away, or to undo an addition.

3. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.

4. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).

5. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,”

6. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away, from A.”

7. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away, from A.”
Hence the statements “five apples take away three apples,”
“three apples are taken away from five apples”
“five apples minus three apples,”
all mean 5
– 3
=2 .

8. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away, from A.”
Hence the statements “five apples take away three apples,”
“three apples are taken away from five apples”
“five apples minus three apples,”
all mean 5
– 3
=2 .

9. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away, from A.”
Hence the statements “five apples take away three apples,”
“three apples are taken away from five apples”
“five apples minus three apples,”
all mean 5
– 3
=2 .
Mayan numerals are visually instructive for subtraction of small
numbers.

10. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away, from A.”
Hence the statements “five apples take away three apples,”
“three apples are taken away from five apples”
“five apples minus three apples,”
all mean 5
– 3
=2 .
Mayan numerals are visually instructive for subtraction of small
numbers. For example,
–
=
signifies 12 – 7 = 5, or that

11. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and it is often
denoted as D and we write that A – B = D (the Difference).
The following phrases are also translated as “A – B”:
“A subtracts B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away, from A.”
Hence the statements “five apples take away three apples,”
“three apples are taken away from five apples”
“five apples minus three apples,”
all mean 5
– 3
=2 .
Mayan numerals are visually instructive for subtraction of small
numbers. For example,
–
=
signifies 12 – 7 = 5, or that
–
=
signifies 13 – 6 = 7.

12. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”

13. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=

14. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–

15. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7

16. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.

17. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.

18. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
For example, 634 – 87:

19. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
For example, 634 – 87:
634
87
–

20. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
when it is necessary.
For example, 634 – 87 is:
634
87
–

21. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
when it is necessary.
need to borrow
For example, 634 – 87 is:
634
87
–

22. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
14
when it is necessary.
2
need to borrow
For example, 634 – 87 is:
634
87
–

23. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
14
when it is necessary.
2
need to borrow
For example, 634 – 87 is:
634
87
–
7

24. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
14
when it is necessary.
2
need to borrow
For example, 634 – 87 is:
634
87
–
7

25. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
12 14
when it is necessary.
need to borrow
5 2
For example, 634 – 87 is:
634
87
–
7

26. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
12 14
when it is necessary.
need to borrow
5 2
For example, 634 – 87 is:
634
87
–
47

27. Subtraction
When there are not enough “ „s” to subtract, we have to convert
a“
” into “
.” This process is called “borrowing.”
For example, 11 – 4 is
–
=
borrow
–
=
=7
More subtraction examples using the Mayan pictorial method are
given in the exercise to help some people to memorize them.
For our base-10 numbers, each borrowed unit is exchanged to
be 10 smaller units.To subtract,
1. lineup the numbers vertically to match the place values,
2. then subtract the digits from right to left and “borrow”
12 14
when it is necessary.
need to borrow
5 2
For example, 634 – 87 is:
634
87
–
5 47

28. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.

29. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.

30. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.

31. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.

32. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 =
78 – 30 =
94 – 20 =

33. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74

34. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.

35. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
For example,
35 – 4 =
63 – 8 =
35 – 7 =

36. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
For example,
35 – 4 = 31
63 – 8 =
35 – 7 =

37. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
For example,
Borrowing
35 – 4 = 31
63 – 8 =
35 – 7 = 28

38. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28

39. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits.

40. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 =
93 – 57 =

41. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 = 53 – 20 – 8
93 – 57 =

42. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 = 53 – 20 – 8
93 – 57 =
= 33 – 8

43. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 = 53 – 20 – 8
93 – 57 =
= 33 – 8 = 25

44. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 = 53 – 20 – 8
93 – 57 = 93 – 50 – 7
= 33 – 8 = 25

45. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 = 53 – 20 – 8
93 – 57 = 93 – 50 – 7
= 43 – 7
= 33 – 8 = 25

46. Subtraction
One should be comfortable with subtracting two two-digit
numbers such as finding the difference between $28 and $45.
Here is one approach that will help one to do that.
Step 1. Memorize the differences between two different digits.
Stop 2. Practice subtracting multiples of 10 from two-digit
numbers.
For example, do the following calculation mentally,
53 – 40 = 13
78 – 30 = 48
94 – 20 = 74
Step 3. Practice subtracting single digits from two-digit numbers,
pay attention to the cases that require borrowing.
After
After
For example,
Borrowing
Borrowing
35 – 4 = 31
63 – 8 = 55
35 – 7 = 28
Step 4. Subtract two two-digit numbers in two steps:
subtract the 10‟s first, then subtract the unit-digits. For example,
53 – 28 = 53 – 20 – 8
93 – 57 = 93 – 50 – 7
= 43 – 7 = 38
= 33 – 8 = 25

47. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =

48. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.

49. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
+
+

50. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
+
=
+

51. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
As noted before that adding two apples to three apples is the
same as adding three apples to two apples – we get five apples.
+
=
+

52. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
As noted before that adding two apples to three apples is the
same as adding three apples to two apples – we get five apples.
+
=
+
We say that addition is commutative, i.e. A + B = B + A.

53. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
As noted before that adding two apples to three apples is the
same as adding three apples to two apples – we get five apples.
+
=
+
We say that addition is commutative, i.e. A + B = B + A.
It makes physical sense to remove two apples from a pile of
five apples – we are left with three apples.
–

54. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
As noted before that adding two apples to three apples is the
same as adding three apples to two apples – we get five apples.
+
=
+
We say that addition is commutative, i.e. A + B = B + A.
It makes physical sense to remove two apples from a pile of
five apples – we are left with three apples. But we can’t do the
reverse, i.e. remove five apples from a pile of two apples.
–

55. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
As noted before that adding two apples to three apples is the
same as adding three apples to two apples – we get five apples.
+
+
=
We say that addition is commutative, i.e. A + B = B + A.
It makes physical sense to remove two apples from a pile of
five apples – we are left with three apples. But we can’t do the
reverse, i.e. remove five apples from a pile of two apples.
–
–
?

56. Subtraction
Your Turn: Do the following subtraction mentally in two steps.
72 – 48 = 72 – 40 – 8 =
84 – 36 = 84 – 30 – 6 =
41 – 28 =
92 – 64 =
This brings up the issue of the order of subtraction.
As noted before that adding two apples to three apples is the
same as adding three apples to two apples – we get five apples.
+
+
=
We say that addition is commutative, i.e. A + B = B + A.
It makes physical sense to remove two apples from a pile of
five apples – we are left with three apples. But we can’t do the
reverse, i.e. remove five apples from a pile of two apples.
–
–
Hence subtraction is not commutative, i.e. A – B ≠ B – A.
?

57. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.

58. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.
Specifically, when subtracting two quantities A and B,
we have to identify clearly that if the problem is
“A – B” or “B – A.”

59. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.
Specifically, when subtracting two quantities A and B,
we have to identify clearly that if the problem is
“A – B” or “B – A.”
Example A. Translate each problem into a subtraction
expression using the given numbers or symbols.
a. The listed price of a Thingamajig is $500. How much money
do we save if we buy one for $400 at Discount Joe?

60. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.
Specifically, when subtracting two quantities A and B,
we have to identify clearly that if the problem is
“A – B” or “B – A.”
Example A. Translate each problem into a subtraction
expression using the given numbers or symbols.
a. The listed price of a Thingamajig is $500. How much money
do we save if we buy one for $400 at Discount Joe?
$500 is more than $400, hence we save 500 – 400 = $100.

61. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.
Specifically, when subtracting two quantities A and B,
we have to identify clearly that if the problem is
“A – B” or “B – A.”
Example A. Translate each problem into a subtraction
expression using the given numbers or symbols.
a. The listed price of a Thingamajig is $500. How much money
do we save if we buy one for $400 at Discount Joe?
$500 is more than $400, hence we save 500 – 400 = $100.
b. If L is the Listed price and D is the Discount Joe’s price,
what are values of L and D in part a. In terms of L and D,
how much do we save if we buy the item at Discount Joe.

62. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.
Specifically, when subtracting two quantities A and B,
we have to identify clearly that if the problem is
“A – B” or “B – A.”
Example A. Translate each problem into a subtraction
expression using the given numbers or symbols.
a. The listed price of a Thingamajig is $500. How much money
do we save if we buy one for $400 at Discount Joe?
$500 is more than $400, hence we save 500 – 400 = $100.
b. If L is the Listed price and D is the Discount Joe’s price,
what are values of L and D in part a. In terms of L and D,
how much do we save if we buy the item at Discount Joe.
With the information from part a. L is the $500 and D is $400.

63. Subtraction
Therefore, unlike addition, because subtraction is not
commutative, we have to establish to order of subtraction.
Specifically, when subtracting two quantities A and B,
we have to identify clearly that if the problem is
“A – B” or “B – A.”
Example A. Translate each problem into a subtraction
expression using the given numbers or symbols.
a. The listed price of a Thingamajig is $500. How much money
do we save if we buy one for $400 at Discount Joe?
$500 is more than $400, hence we save 500 – 400 = $100.
b. If L is the Listed price and D is the Discount Joe’s price,
what are values of L and D in part a. In terms of L and D,
how much do we save if we buy the item at Discount Joe.
With the information from part a. L is the $500 and D is $400.
The amount saved is 500 – 400 = 100,

64. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
108th floor
top

65. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
108th floor
top
42th floor
1st hr

66. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
108th floor
top
67th floor
nd
2
hr
42th floor
1st hr

67. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
67th floor
nd
2
hr
42th floor
1st hr

68. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
108th floor
top
After 1 hour we were at the 42nd
67th floor
2nd hr
floor. After two hours, we were at
42th floor
the 67th floor.
1st hr
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
After the 1st hour, we still have 108 – 42 = 66 floors to the top.

69. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
108th floor
top
After 1 hour we were at the 42nd
67th floor
2nd hr
floor. After two hours, we were at
42th floor
the 67th floor.
1st hr
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.

70. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
108th floor
top
After 1 hour we were at the 42nd
67th floor
2nd hr
floor. After two hours, we were at
42th floor
the 67th floor.
1st hr
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.

71. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
108th floor
top
After 1 hour we were at the 42nd
67th floor
2nd hr
floor. After two hours, we were at
42th floor
the 67th floor.
1st hr
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
108th fl.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.
Nth fl.

72. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
108th floor
top
After 1 hour we were at the 42nd
67th floor
2nd hr
floor. After two hours, we were at
42th floor
the 67th floor.
1st hr
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
108th fl.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.
?
Nth fl.

73. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
108th floor
top
After 1 hour we were at the 42nd
67th floor
2nd hr
floor. After two hours, we were at
42th floor
the 67th floor.
1st hr
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
108th fl.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.
Nth
We are on the
floor out of total 108 floors,
so the number of remaining floors to the top
is 108 – N as shown.
?
Nth fl.

74. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first,

75. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first,
+
+

76. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first,
+
+

77. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first,
+
+
+
+

78. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first,
+
+
+
=
+

79. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
=
+

80. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
=
We say that “the addition is associative.”
+

81. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.

82. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–

83. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–
–

84. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–
–

85. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–
–
–
–

86. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–
–
–
–
–

87. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–
–
–
≠
–
–

88. Subtraction
If we are gathering three piles of apples, it does not matter which
two piles we group together first, i.e. A + (B + C) = (A + B) + C
where the “( )” means “do first.”
+
+
+
+
=
We say that “the addition is associative.”
But the results of “subtracting” three piles of apples depends on
the order of the removals.
–
–
–
–
≠
–
–
So subtraction is not associative, i.e. (A – B) – C ≠ A – (B – C).

89. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).

90. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).
We treat 6 – 3 – 2 as (6 – 3) – 2, i.e. take away 3, then take
away another 2, therefore we take away 5 in total.

91. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).
We treat 6 – 3 – 2 as (6 – 3) – 2, i.e. take away 3, then take
away another 2, therefore we take away 5 in total.
In other words, 6 – 3 – 2 = 6 – (3 + 2) = 6 – 5 = 1.

92. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).
We treat 6 – 3 – 2 as (6 – 3) – 2, i.e. take away 3, then take
away another 2, therefore we take away 5 in total.
In other words, 6 – 3 – 2 = 6 – (3 + 2) = 6 – 5 = 1.
Hence for a multi–subtraction, we may total the quantities that
are to be taken away first then subtract.

93. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).
We treat 6 – 3 – 2 as (6 – 3) – 2, i.e. take away 3, then take
away another 2, therefore we take away 5 in total.
In other words, 6 – 3 – 2 = 6 – (3 + 2) = 6 – 5 = 1.
Hence for a multi–subtraction, we may total the quantities that
are to be taken away first then subtract. In symbols,
A – B – C = A – (B + C)
and in general, A – B – C – D – . . = A – (B + C + D + ..)

94. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).
We treat 6 – 3 – 2 as (6 – 3) – 2, i.e. take away 3, then take
away another 2, therefore we take away 5 in total.
In other words, 6 – 3 – 2 = 6 – (3 + 2) = 6 – 5 = 1.
Hence for a multi–subtraction, we may total the quantities that
are to be taken away first then subtract. In symbols,
A – B – C = A – (B + C)
and in general, A – B – C – D – . . = A – (B + C + D + ..)
Furthermore, for a mixed problem, we may separate the
addition and the subtraction into two groups, find the total of
each group, then find the difference of two totals, or that,

95. Subtraction
So when subtracting two or more numbers in a row, we can’t
arbitrarily subtract the ones in the back as shown that
(6 – 3) – 2 ≠ 6 – (3 – 2).
We treat 6 – 3 – 2 as (6 – 3) – 2, i.e. take away 3, then take
away another 2, therefore we take away 5 in total.
In other words, 6 – 3 – 2 = 6 – (3 + 2) = 6 – 5 = 1.
Hence for a multi–subtraction, we may total the quantities that
are to be taken away first then subtract. In symbols,
A – B – C = A – (B + C)
and in general, A – B – C – D – . . = A – (B + C + D + ..)
Furthermore, for a mixed problem, we may separate the
addition and the subtraction into two groups, find the total of
each group, then find the difference of two totals, or that,
A – a + B – b + C – c . . = (A + B + C ..) – (a + b + c ..)

96. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
b. 82 – 12 – 7 – 8 – 14 – 23

97. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
b. 82 – 12 – 7 – 8 – 14 – 23

98. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23

99. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18

100. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44

101. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44
= 82 – (16 + 44)

102. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44
= 82 – (16 + 44)
= 82 – 60 = 22

103. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44
= 82 – (16 + 44)
= 82 – 60 = 22
Find the total reduction first.
82 – 12 – 7 – 8 – 14 – 23

104. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44
= 82 – (16 + 44)
= 82 – 60 = 22
Find the total reduction first.
82 – 12 – 7 – 8 – 14 – 23
= 82 – (12 + 7 + 8 + 14 + 23)

105. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44
= 82 – (16 + 44)
= 82 – 60 = 22
Find the total reduction first.
82 – 12 – 7 – 8 – 14 – 23
= 82 – (12 + 7 + 8 + 14 + 23)
20
30

106. Subtraction
Example C. Calculate each of the following problems using
two different ways. Do it from left to right in the order given
and do it by calculating the total reduction first.
a. 82 – 16 – 44
Do it in the given order.
82 – 16 – 44
= 66 – 44
= 22
b. 82 – 12 – 7 – 8 – 14 – 23
Do it in the given order.
82 – 12 – 7 – 8 – 14 – 23
= 70 – 7 – 8 – 14 – 23
= 63 – 8 – 14 – 23
= 55 – 14 – 23
= 41 – 23
= 18
Find the total reduction first.
82 – 16 – 44
= 82 – (16 + 44)
= 82 – 60 = 22
Find the total reduction first.
82 – 12 – 7 – 8 – 14 – 23
= 82 – (12 + 7 + 8 + 14 + 23)
= 82 – 64
= 18
20
30

107. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23

108. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
82 – 12 – 7 + 8 + 14 – 23

109. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23

110. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 63 + 8 + 14 – 23
= 71 + 14 – 23
= 85 – 23
= 62

111. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
Group into two groups.
82 – 12 – 7 + 8 + 14 – 23 82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 63 + 8 + 14 – 23
= 71 + 14 – 23
= 85 – 23
= 62

112. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
Group into two groups.
82 – 12 – 7 + 8 + 14 – 23 82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 82 + 8 + 14 – (12 + 7 + 23)
= 63 + 8 + 14 – 23
= 71 + 14 – 23
= 85 – 23
= 62

113. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
Group into two groups.
82 – 12 – 7 + 8 + 14 – 23 82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 82 + 8 + 14 – (12 + 7 + 23)
= 63 + 8 + 14 – 23
30
90
= 71 + 14 – 23
= 85 – 23
= 62

114. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
Group into two groups.
82 – 12 – 7 + 8 + 14 – 23 82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 82 + 8 + 14 – (12 + 7 + 23)
= 63 + 8 + 14 – 23
30
90
= 71 + 14 – 23
= 104 – 42
= 85 – 23
= 62
= 62

115. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
Group into two groups.
82 – 12 – 7 + 8 + 14 – 23 82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 82 + 8 + 14 – (12 + 7 + 23)
= 63 + 8 + 14 – 23
30
90
= 71 + 14 – 23
= 104 – 42
= 85 – 23
= 62
= 62
Subtracting quantities in the wrong order is one of the most
common mistakes in mathematics (addition requires no such
fuss).

116. Subtraction
c. 82 – 12 – 7 + 8 + 14 – 23
Do it in the given order.
Group into two groups.
82 – 12 – 7 + 8 + 14 – 23 82 – 12 – 7 + 8 + 14 – 23
= 70 – 7 + 8 + 14 – 23
= 82 + 8 + 14 – (12 + 7 + 23)
= 63 + 8 + 14 – 23
30
90
= 71 + 14 – 23
= 104 – 42
= 85 – 23
= 62
= 62
Subtracting quantities in the wrong order is one of the most
common mistakes in mathematics (addition requires no such
fuss).
When reading mathematical expressions or translating
real life problems involving subtraction into mathematics,
always ask the question “who subtracts whom?”
Answer it clearly, then proceed.