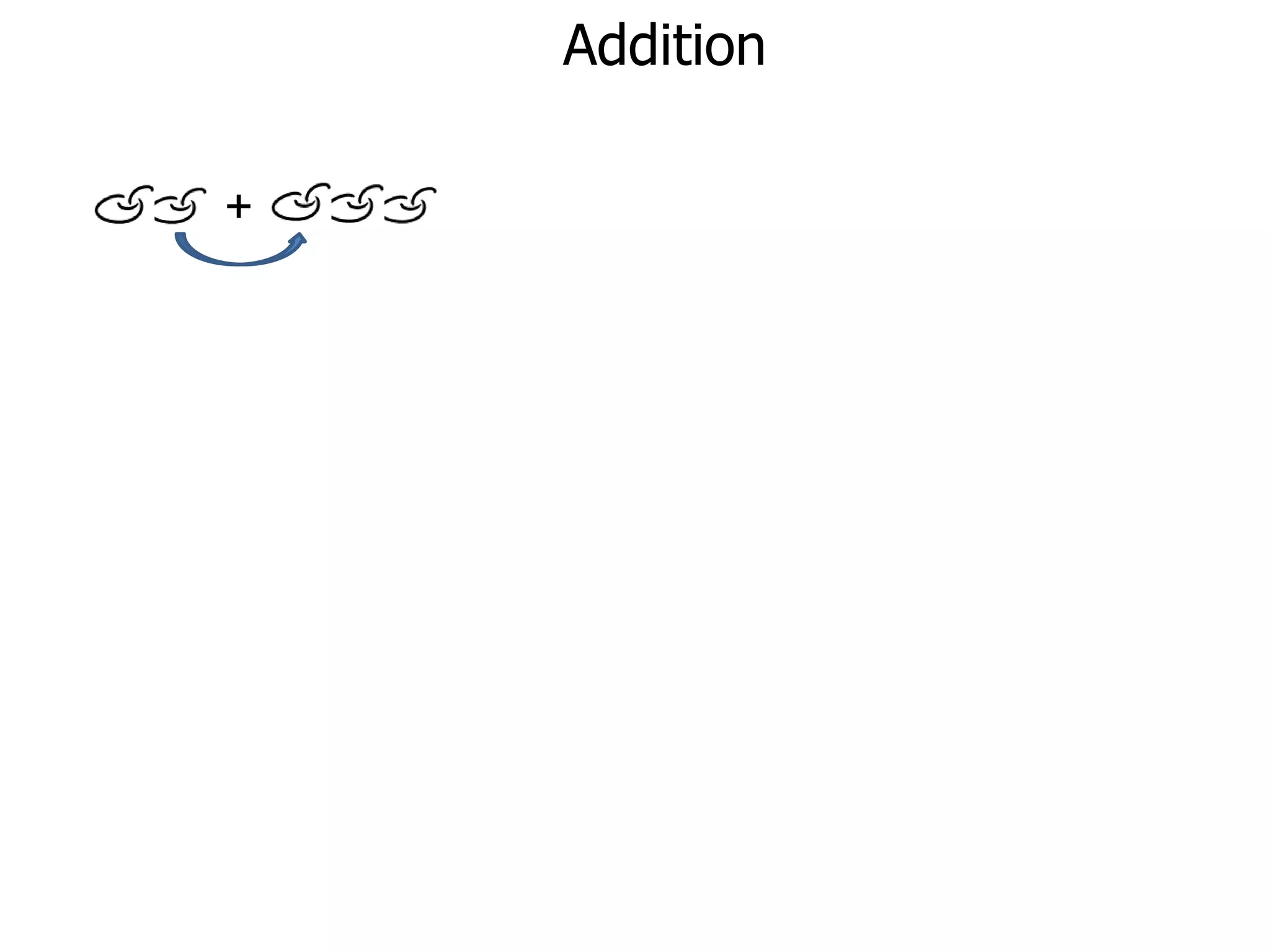
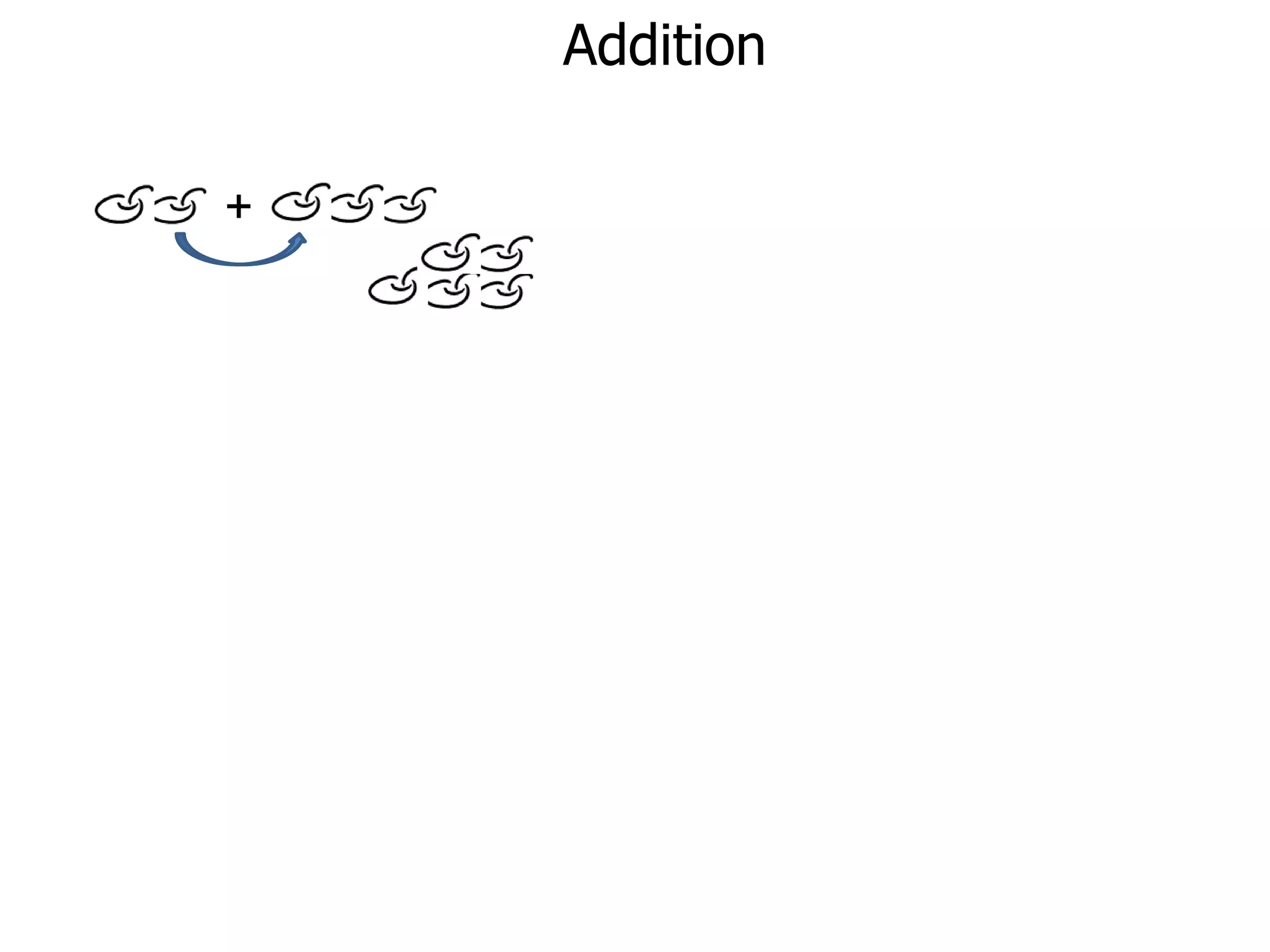
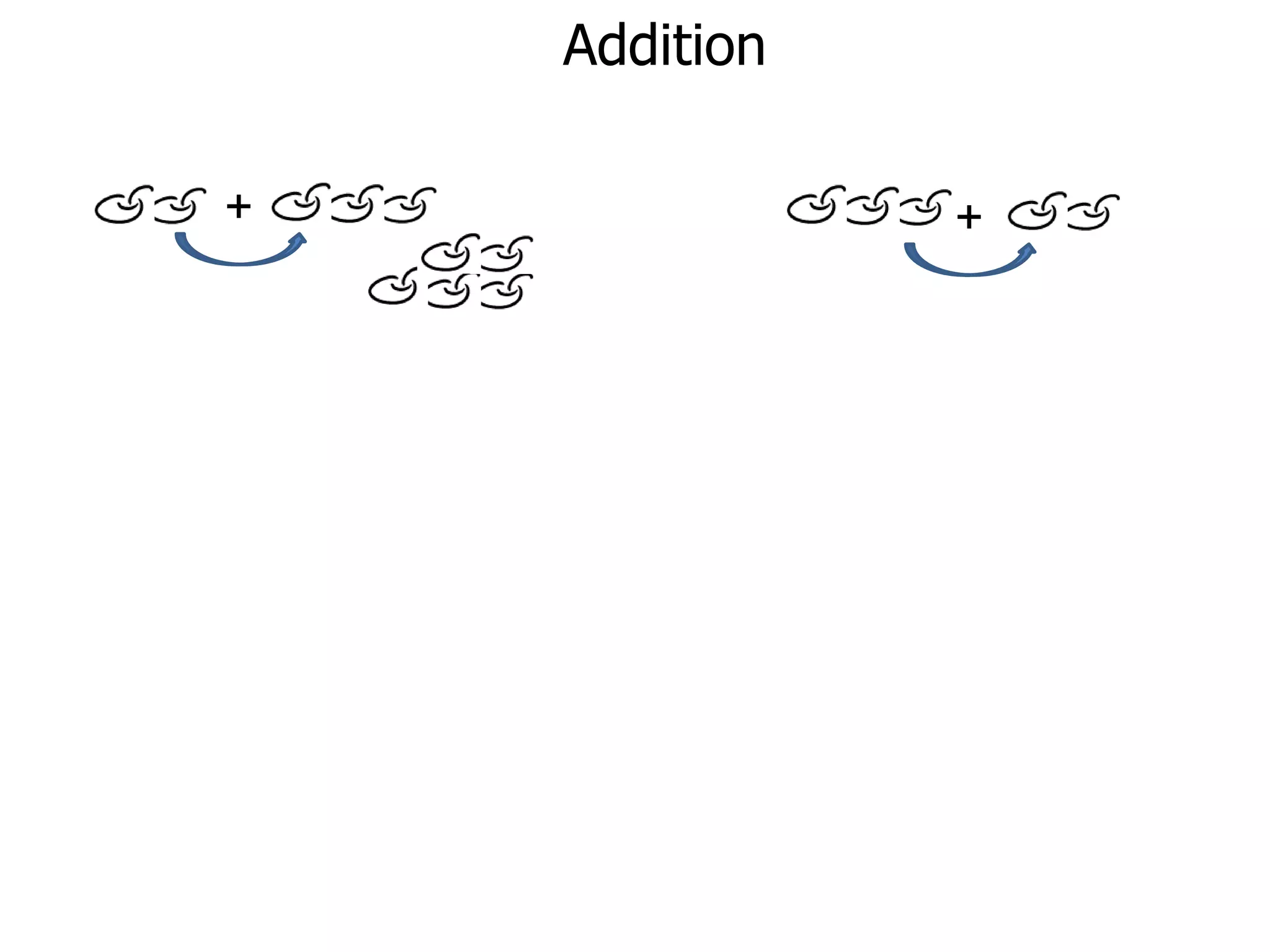
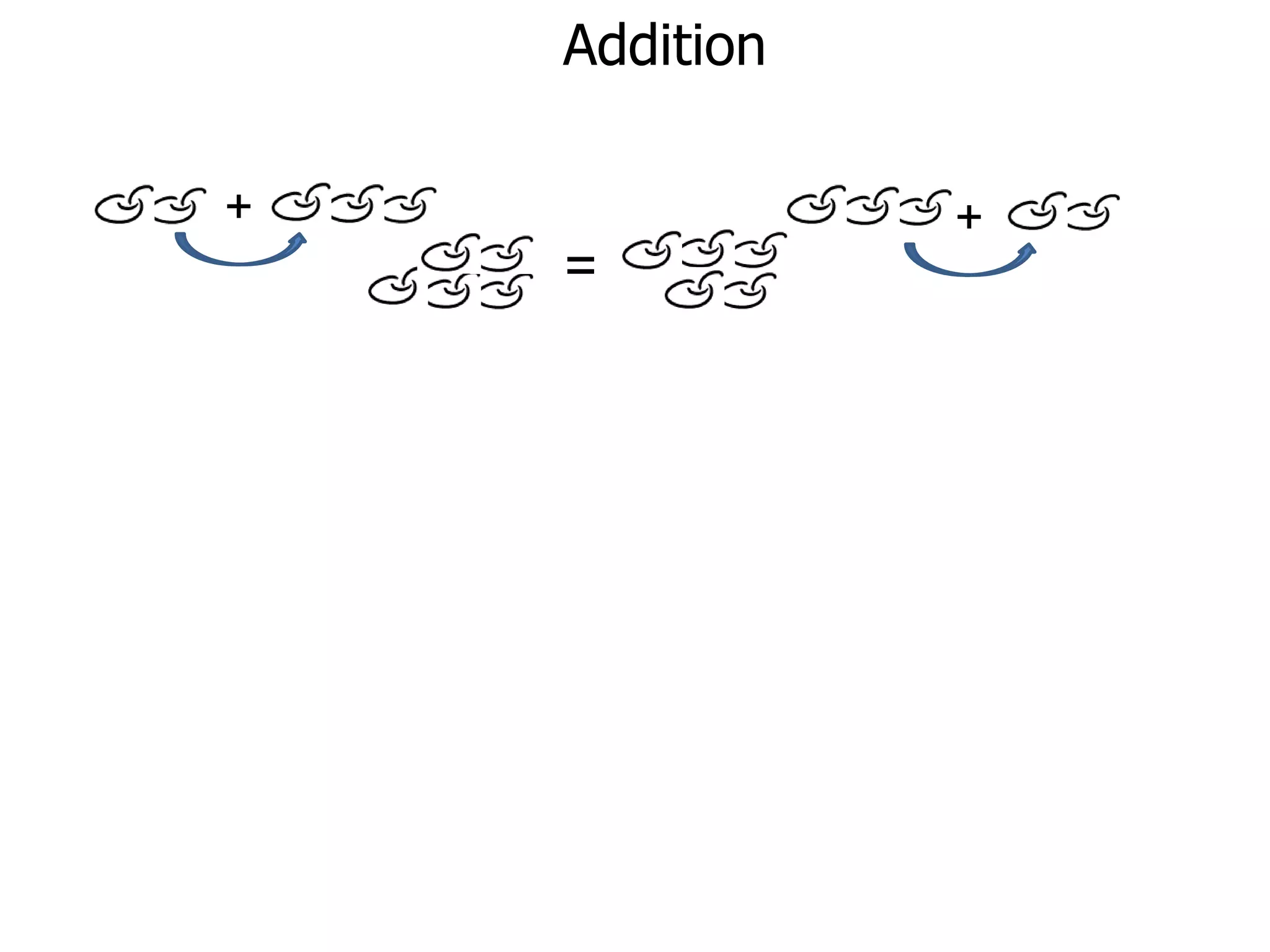
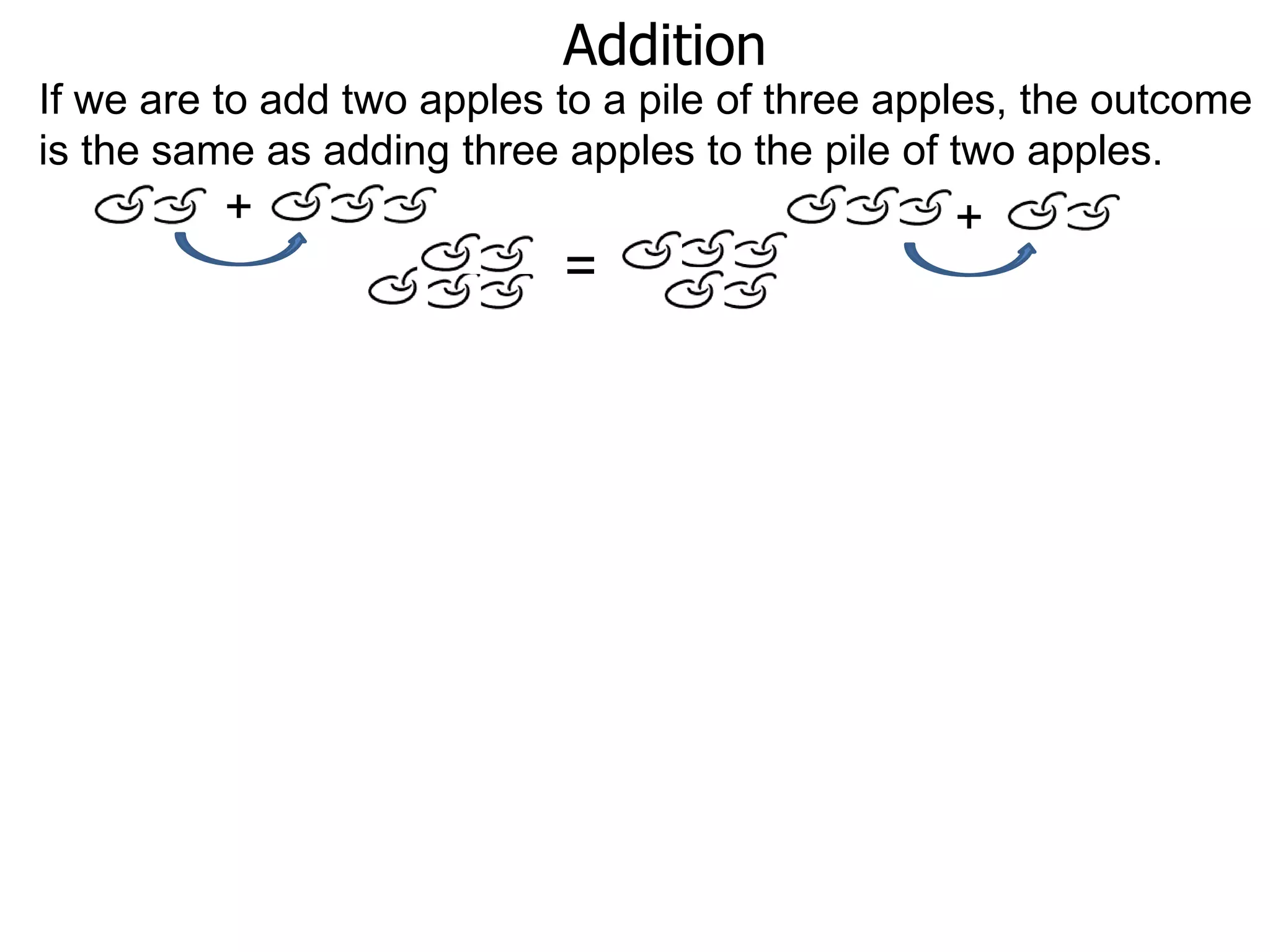
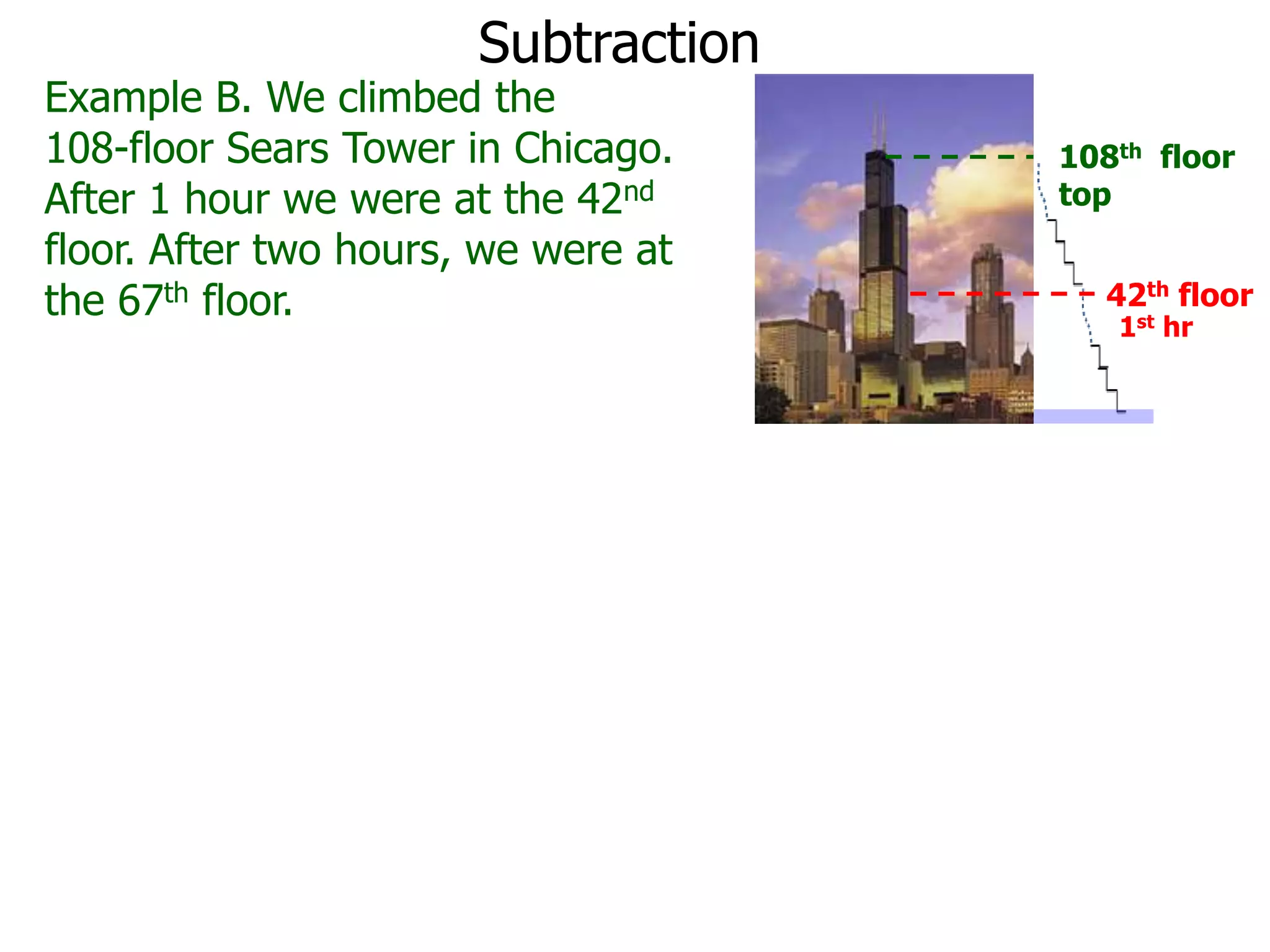
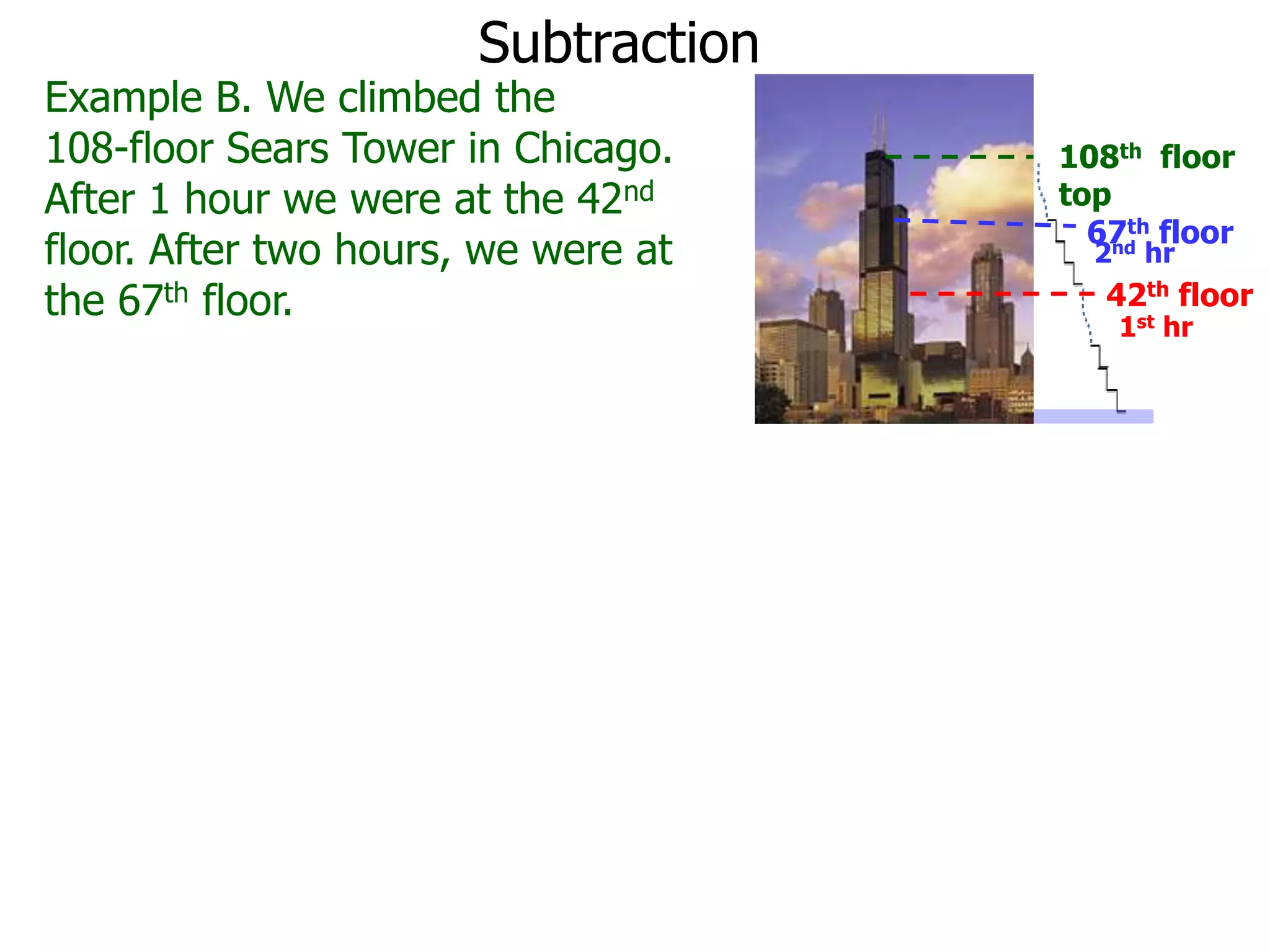
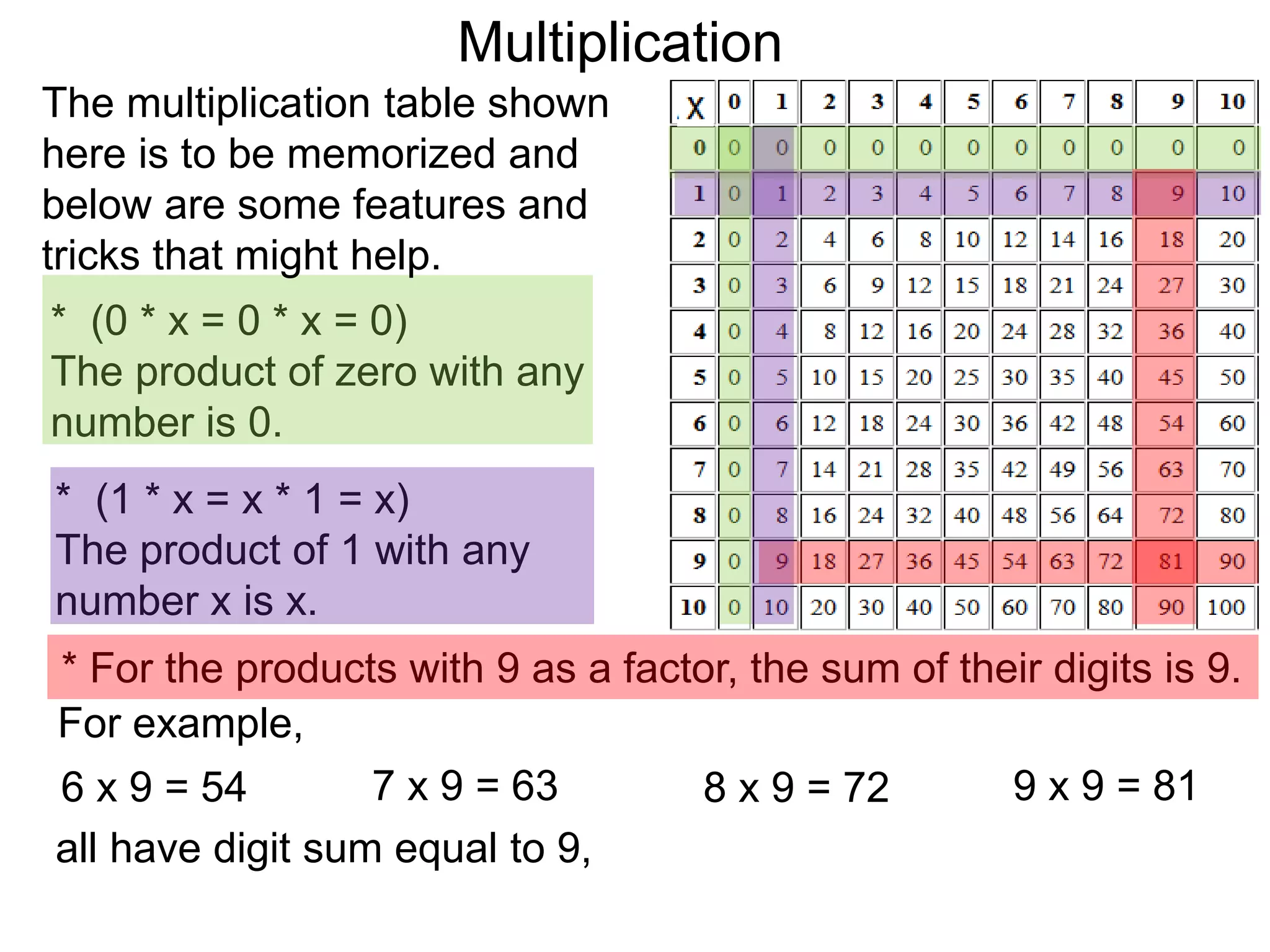
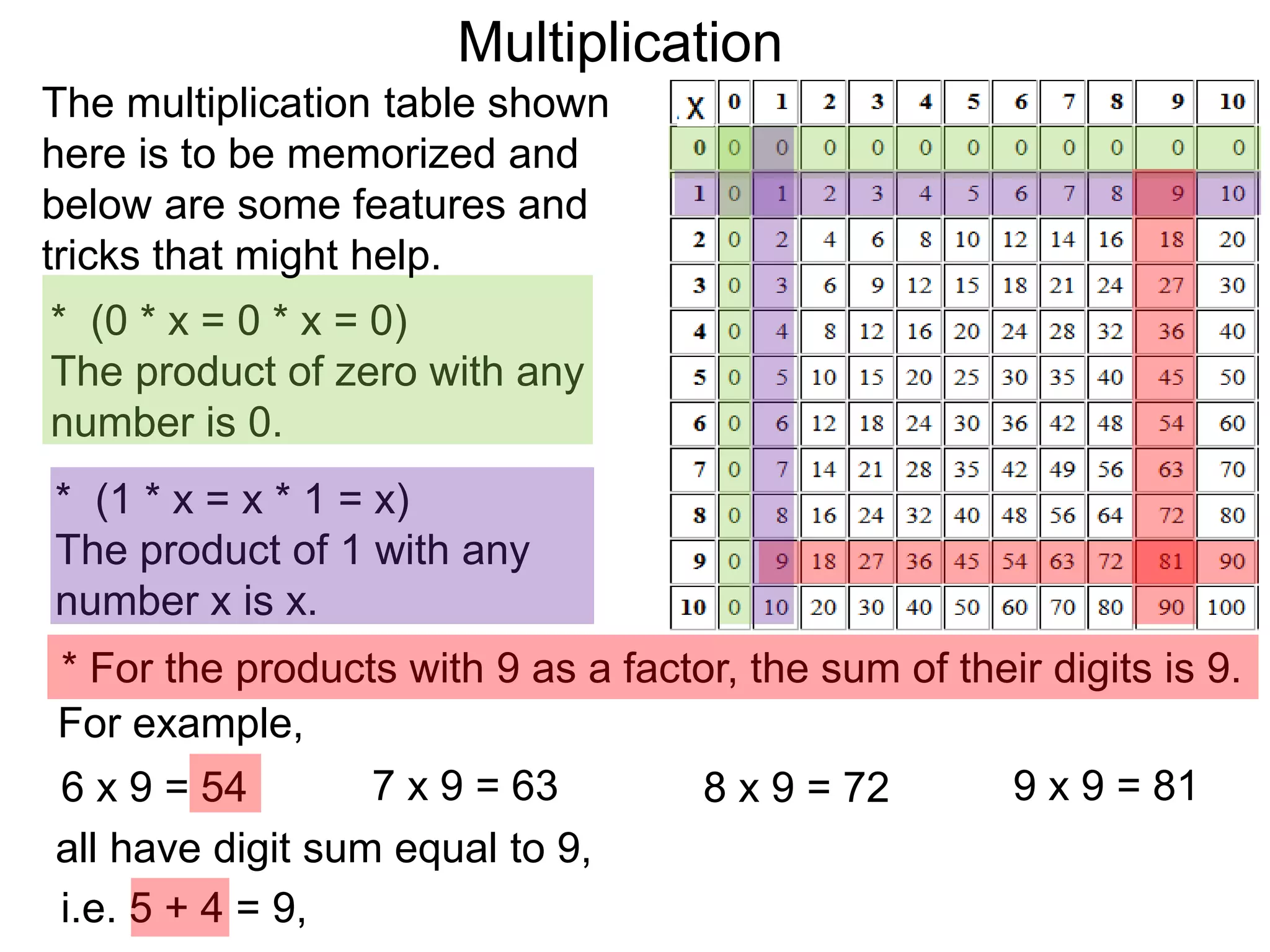
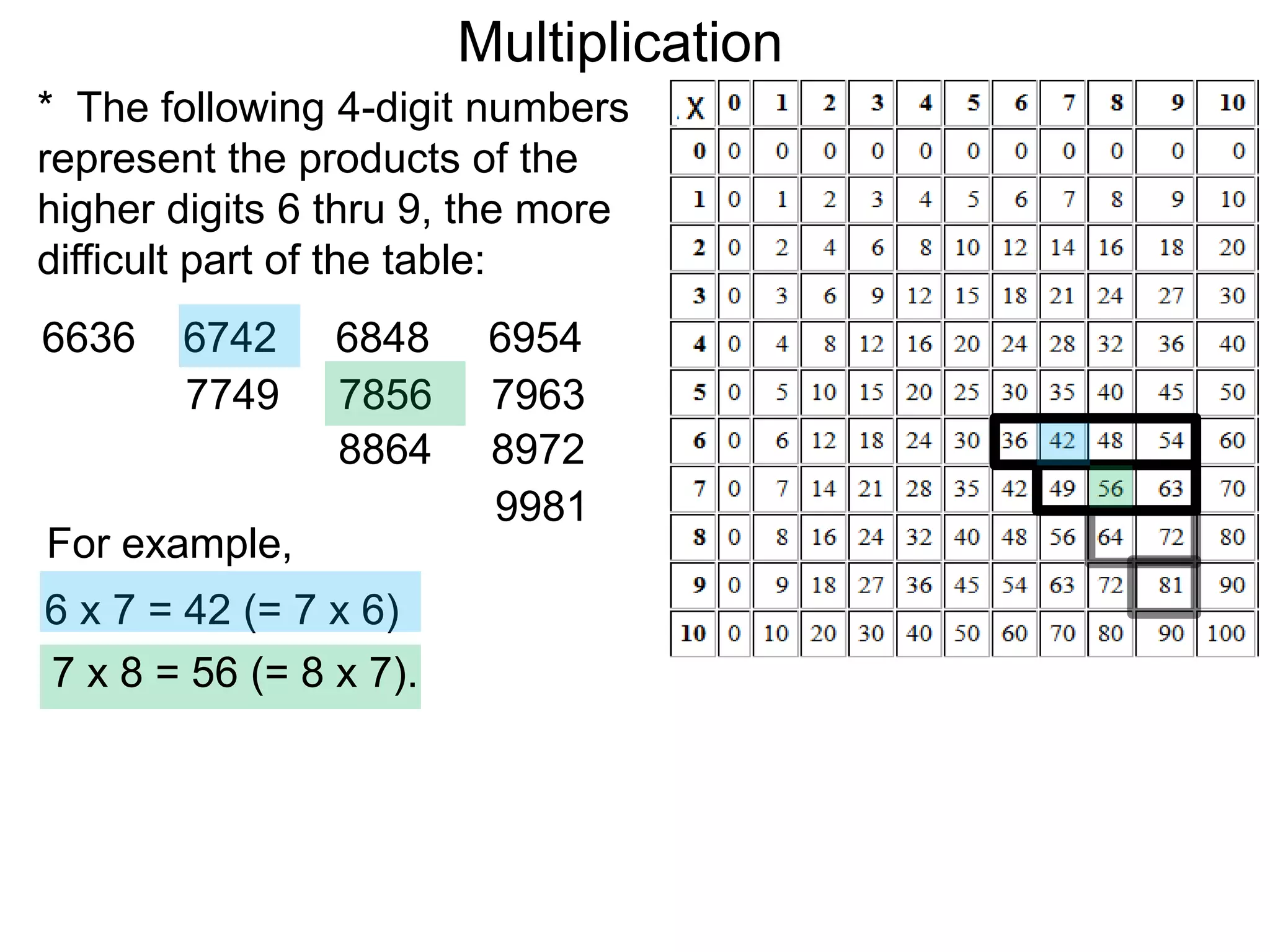
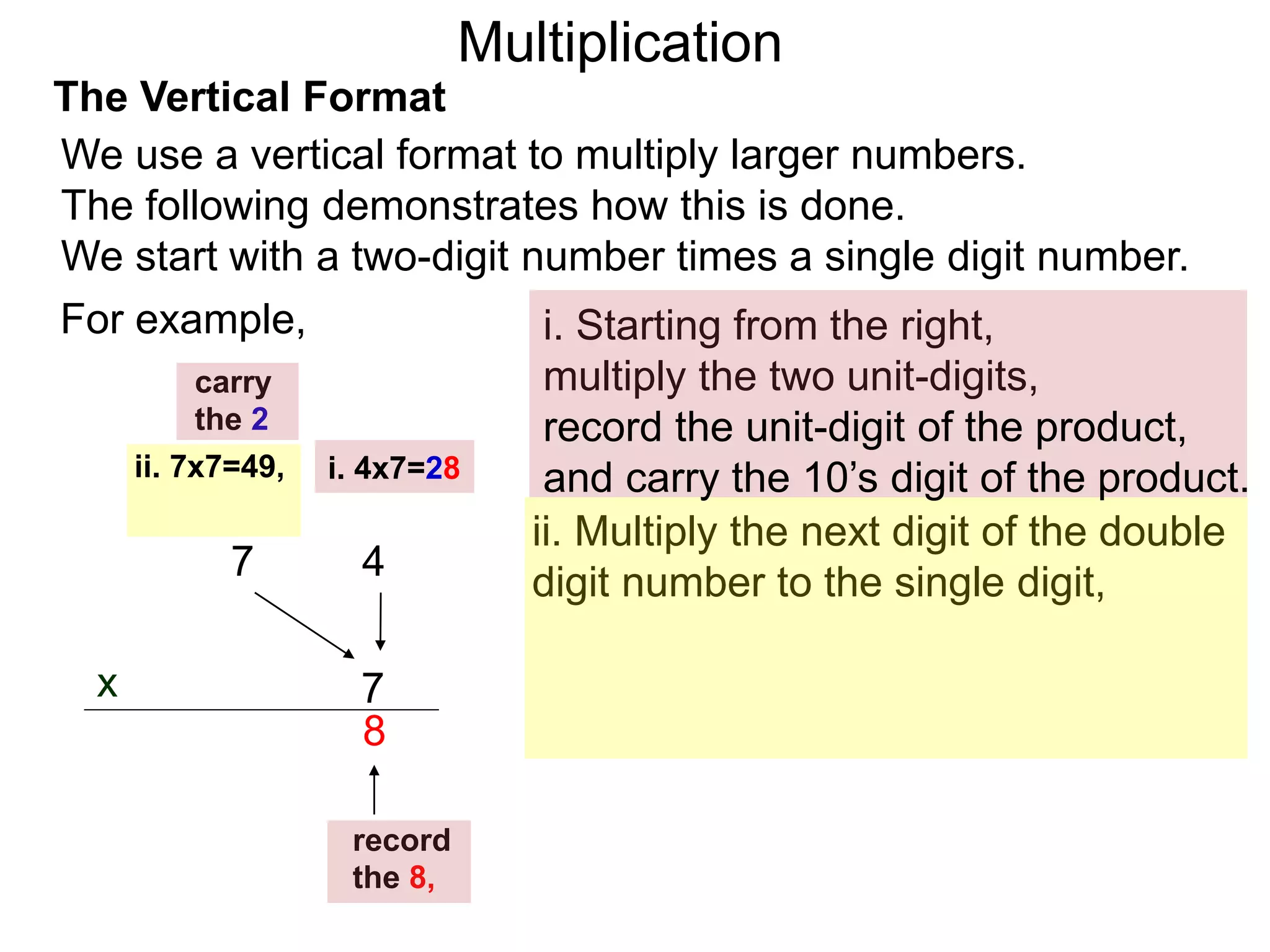
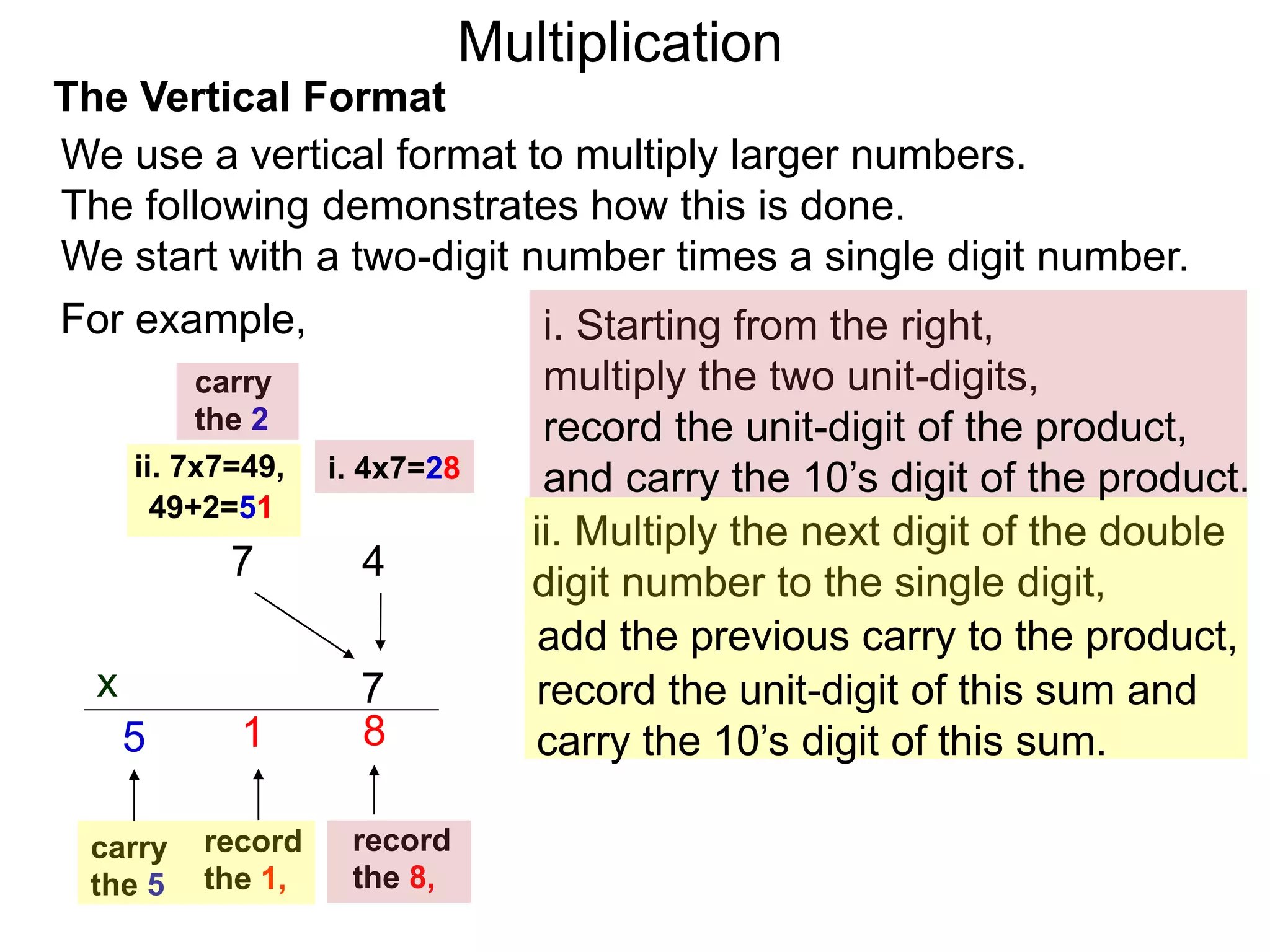
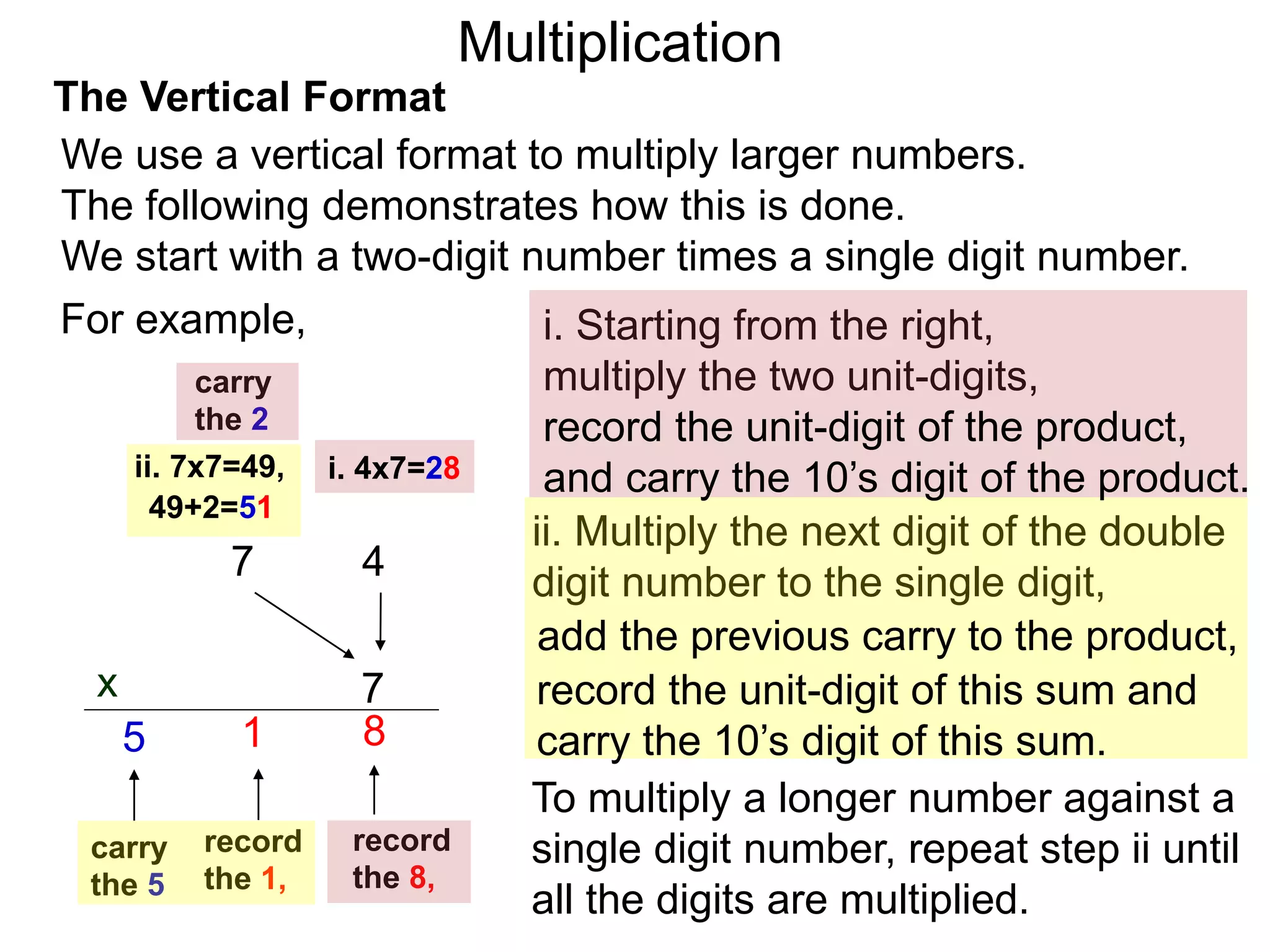
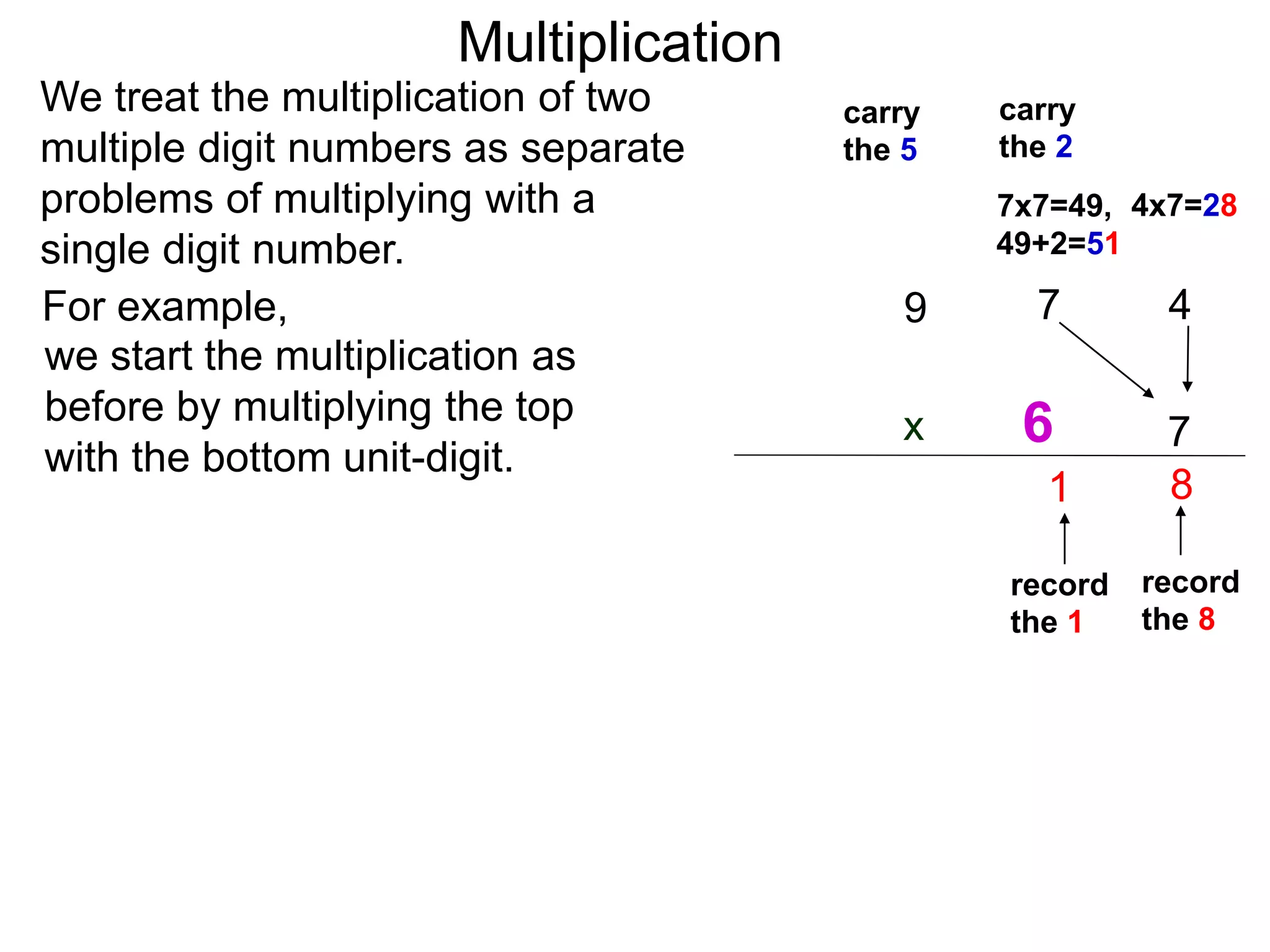
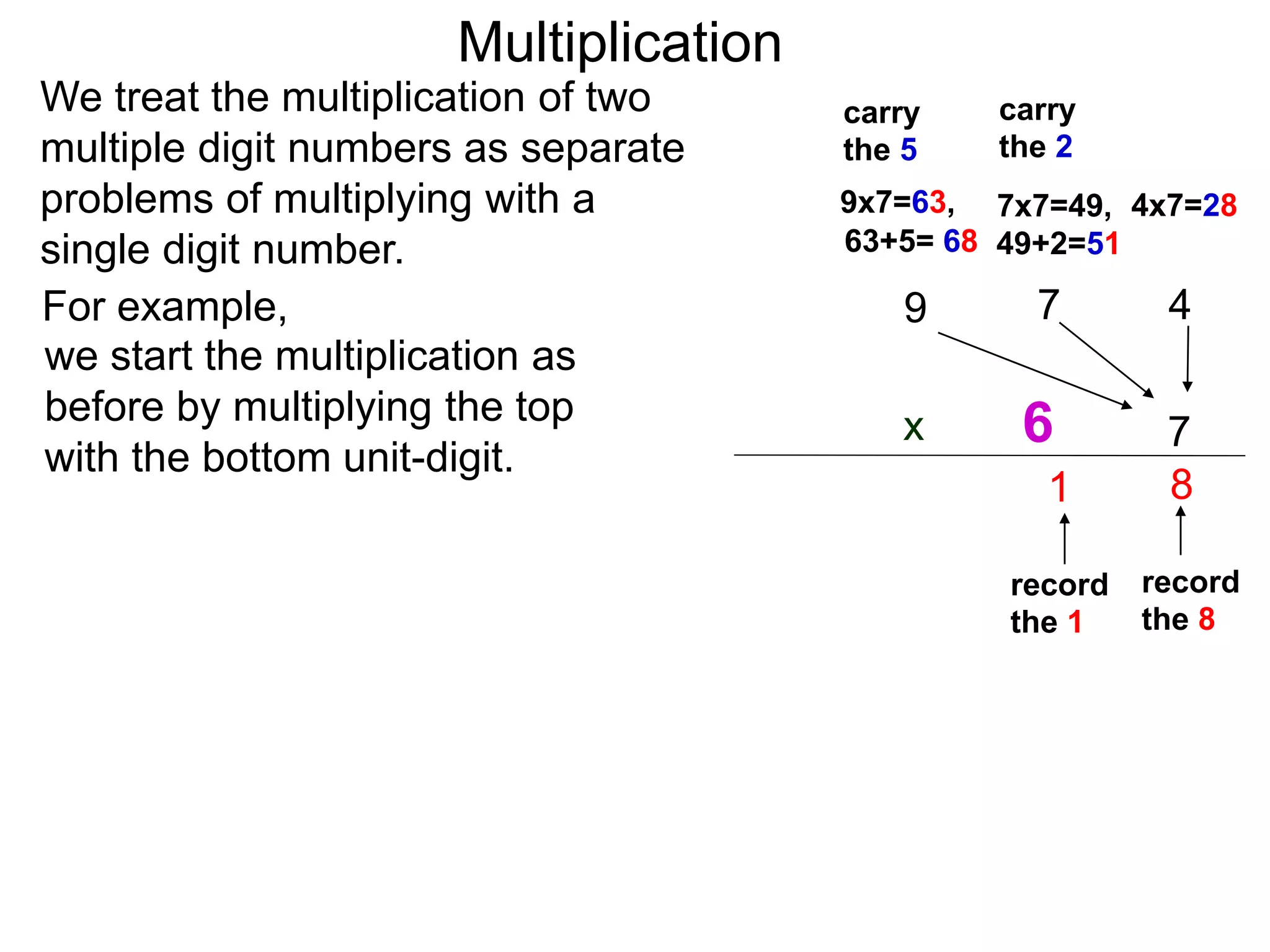
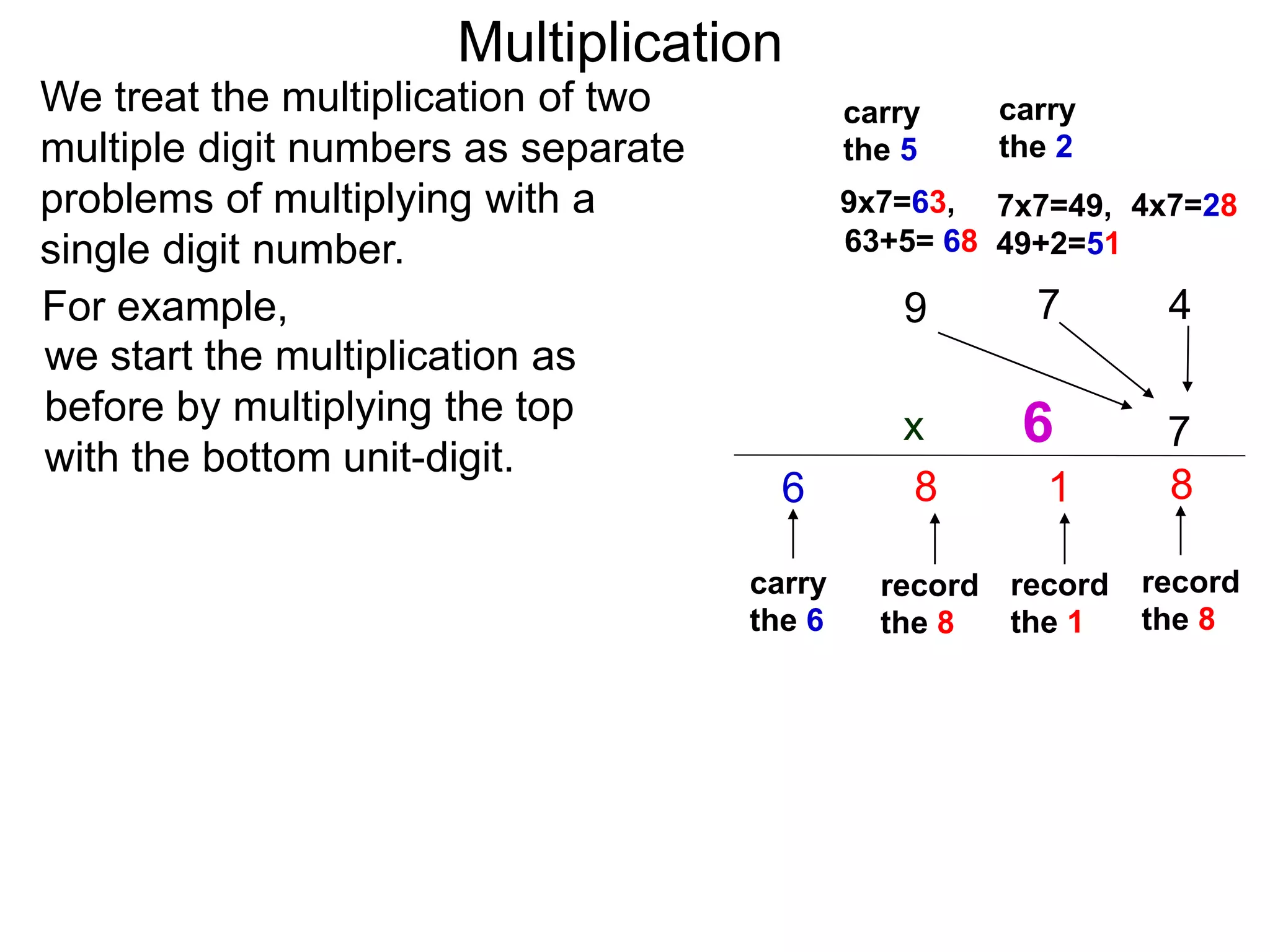
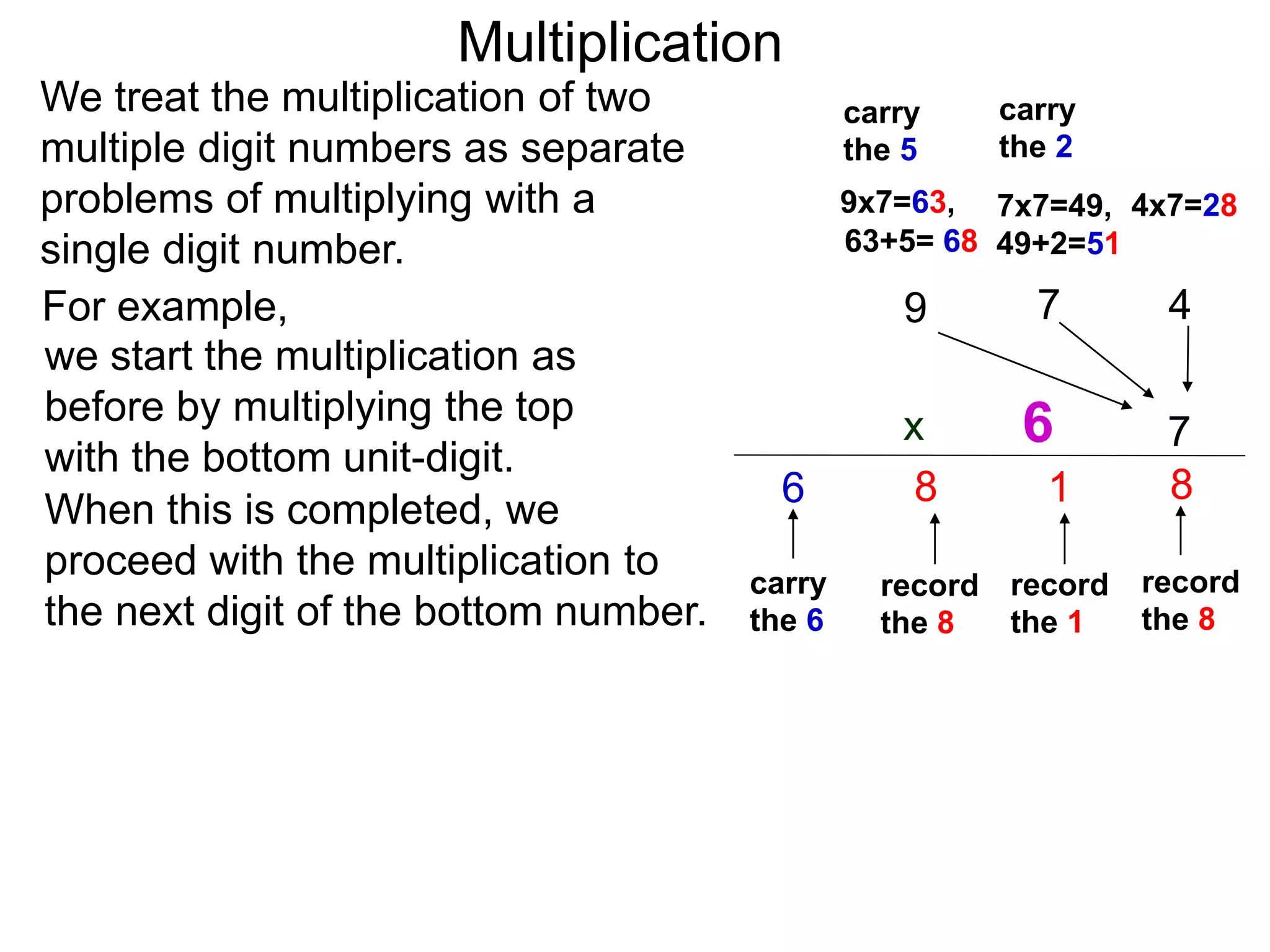
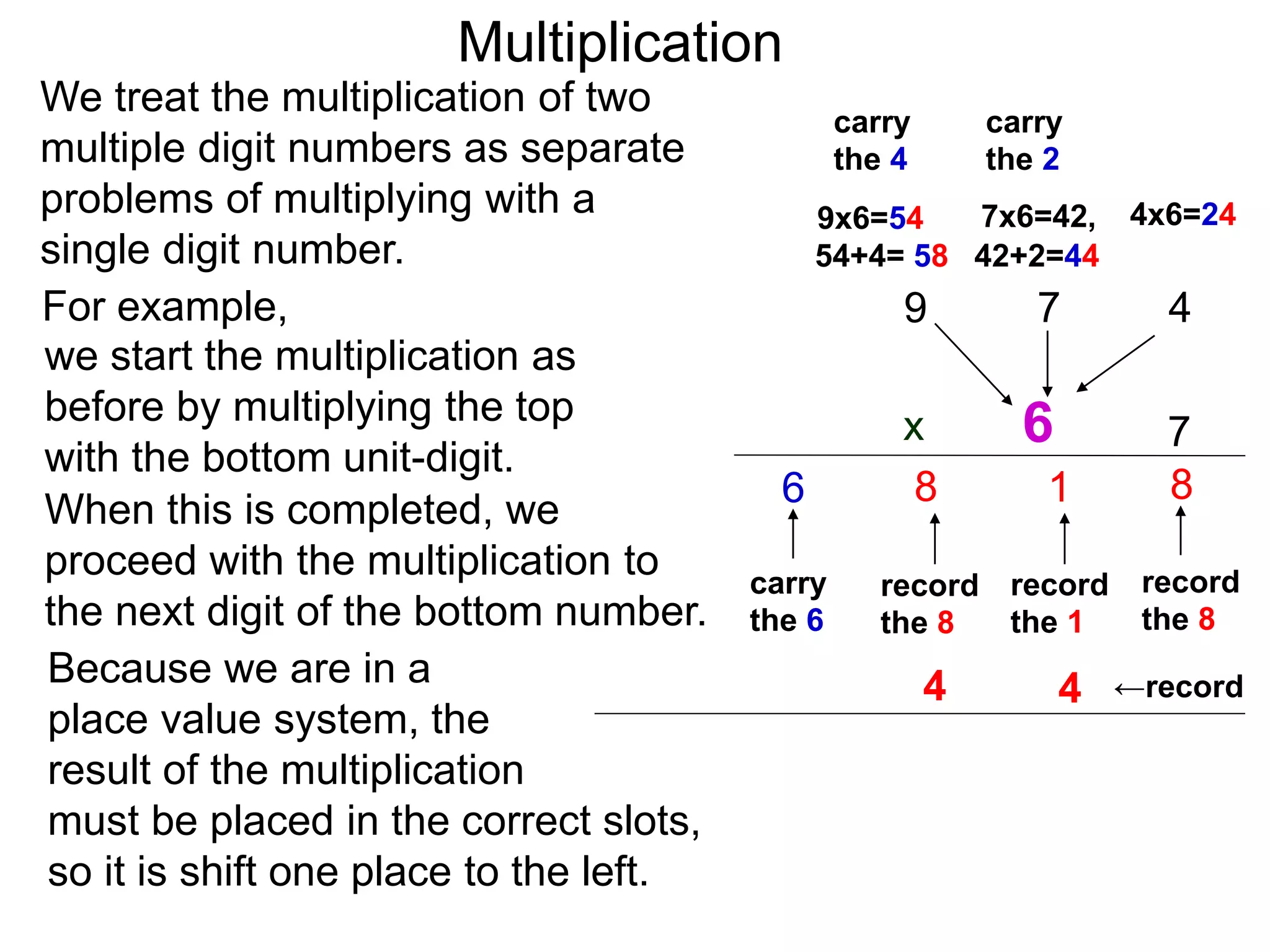
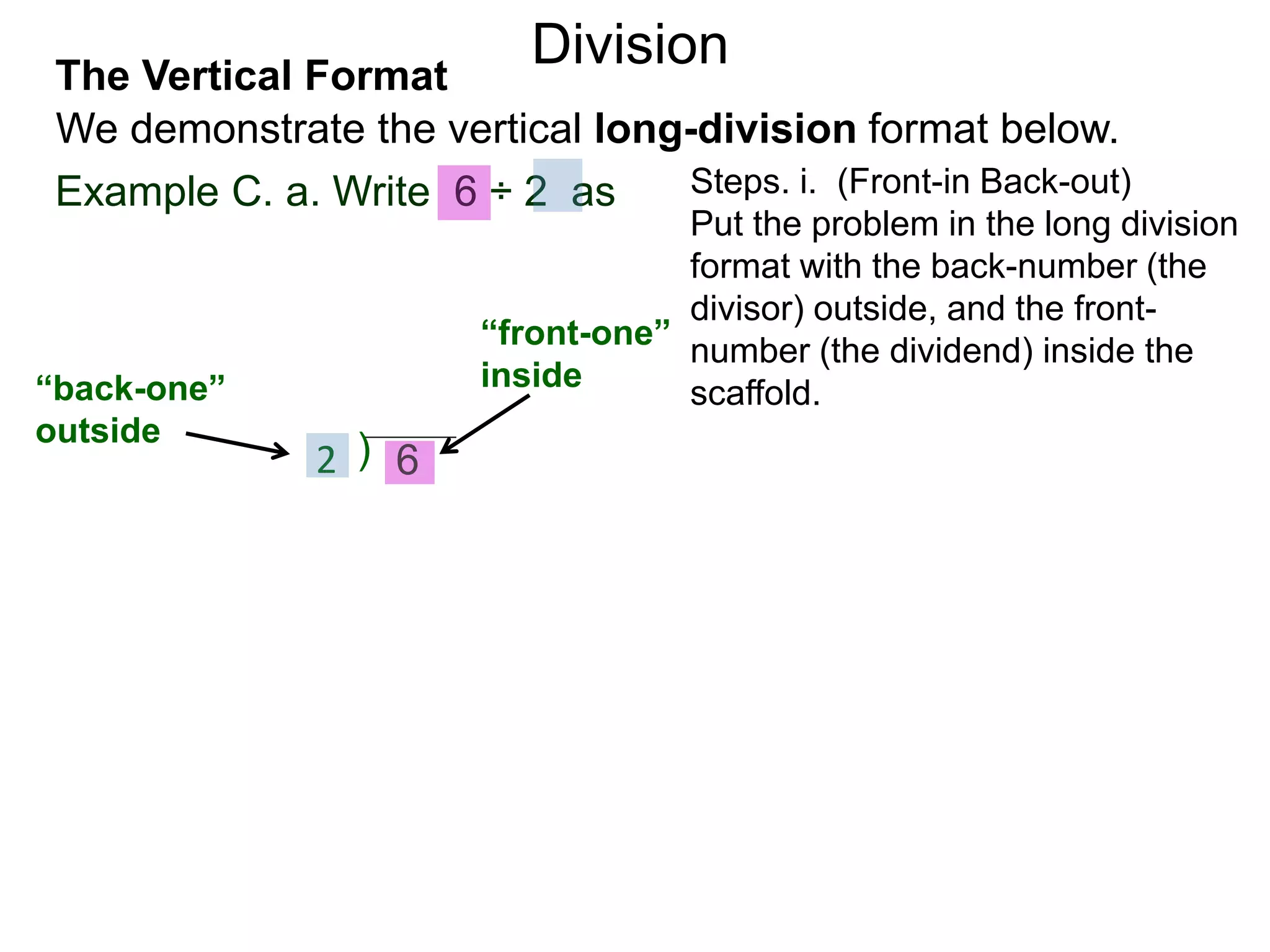
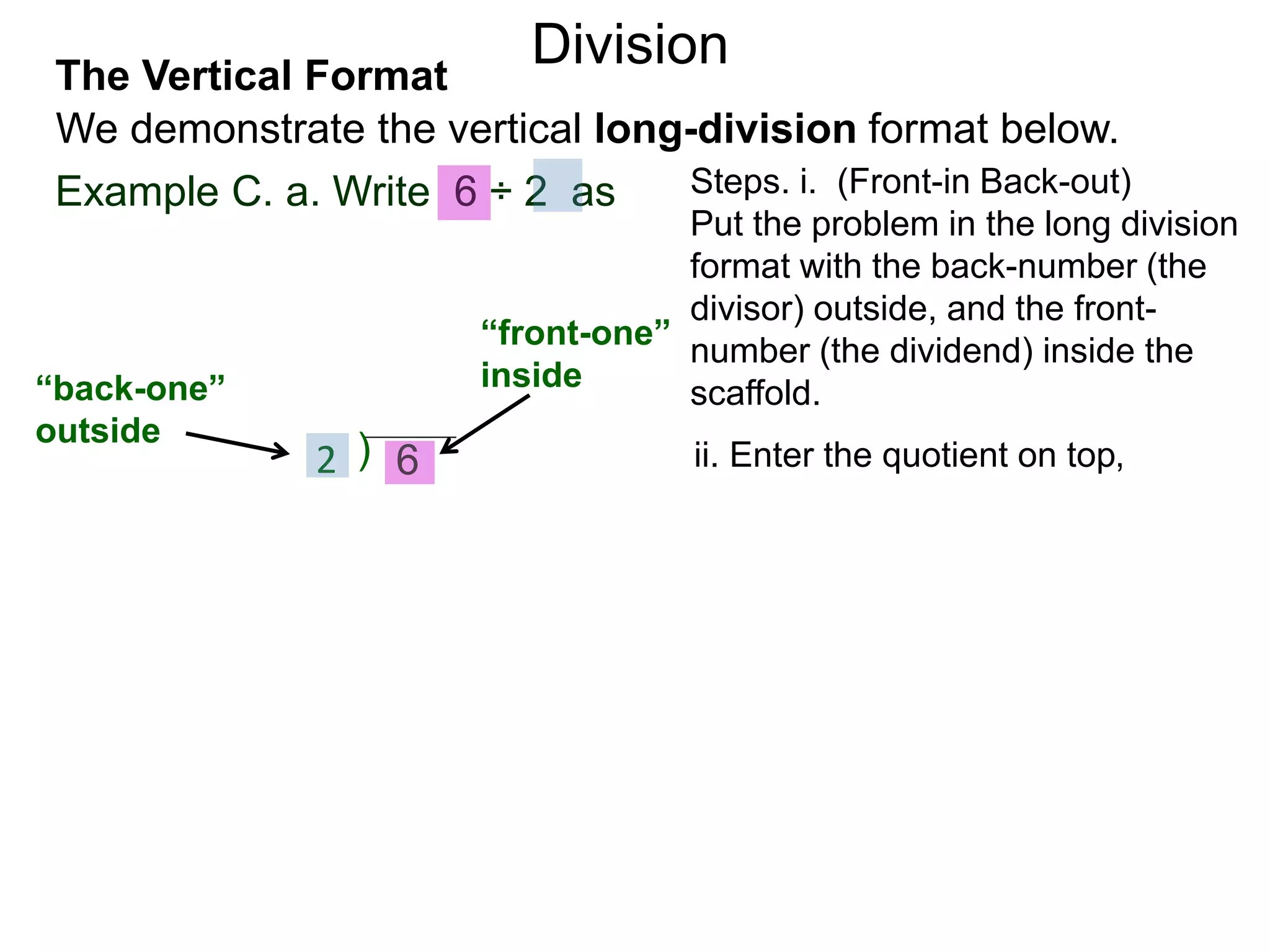
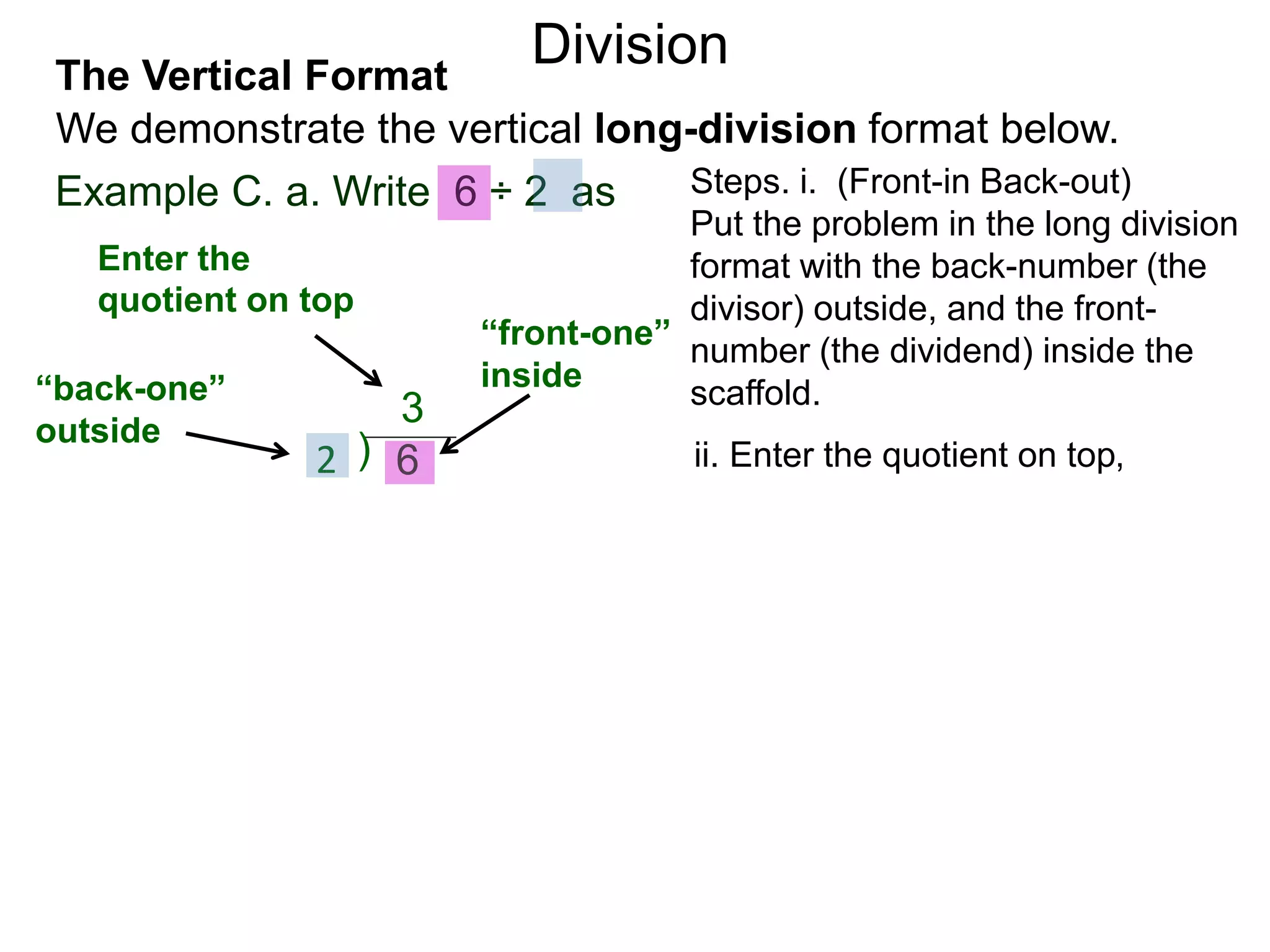
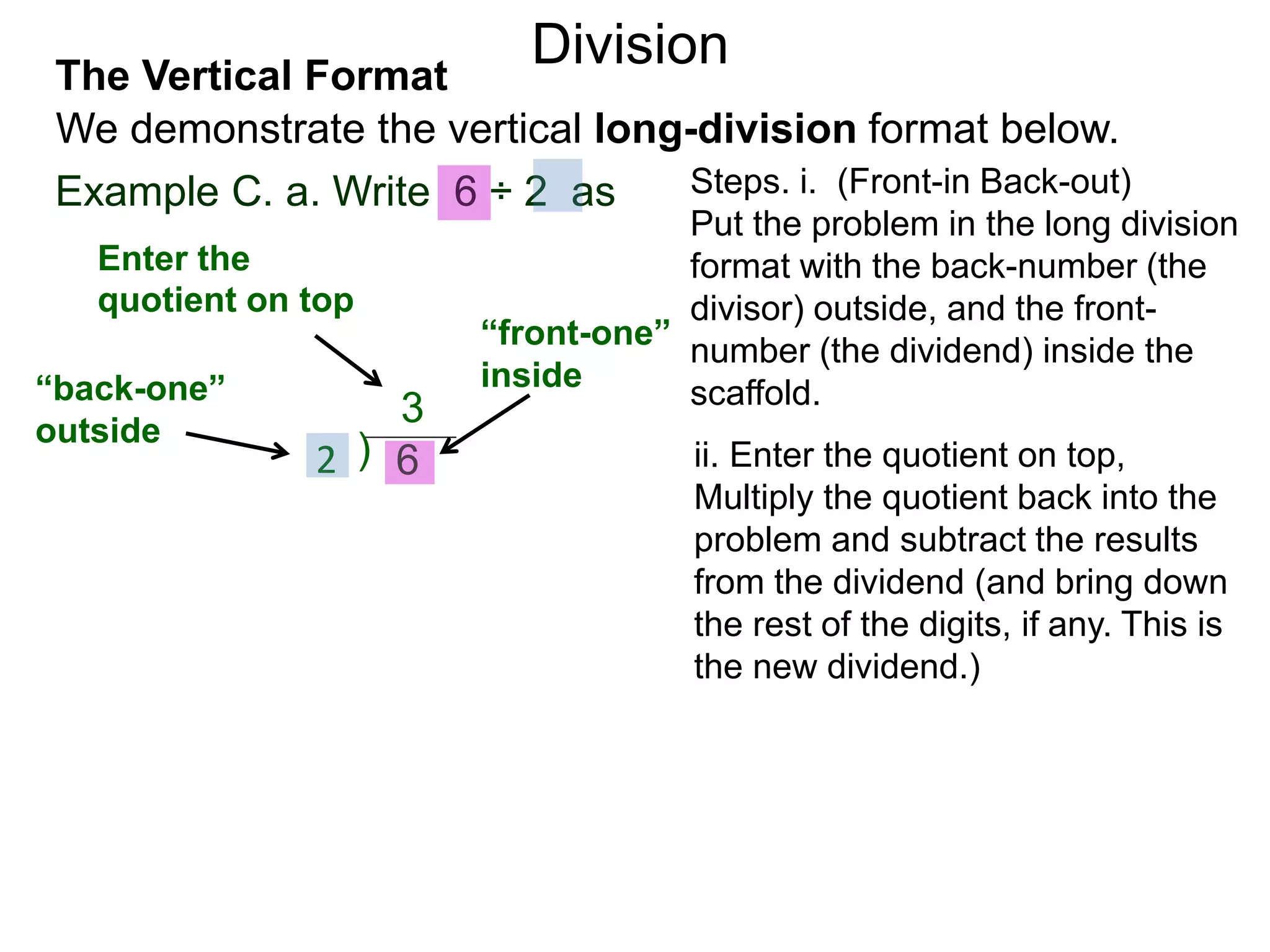
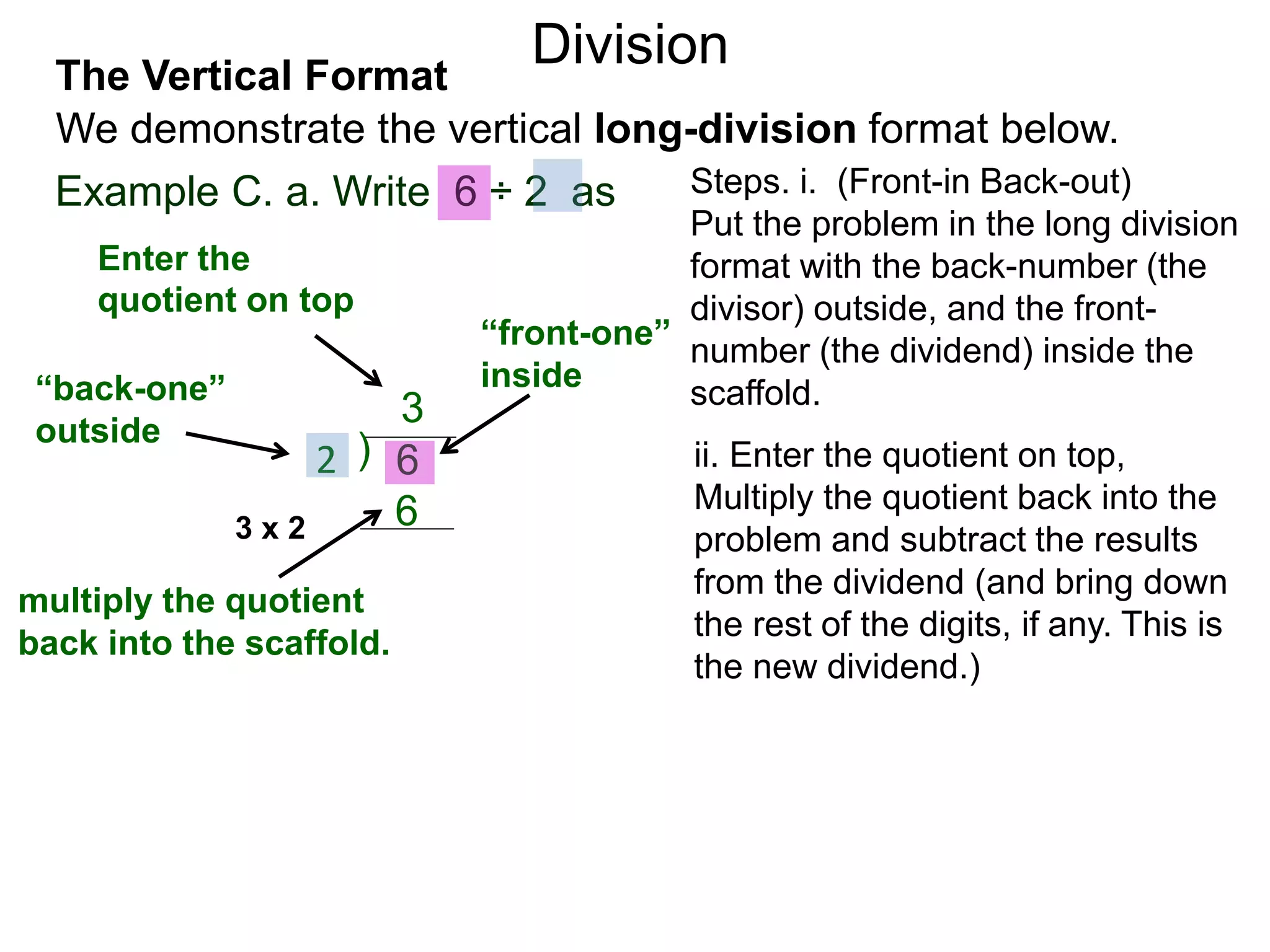
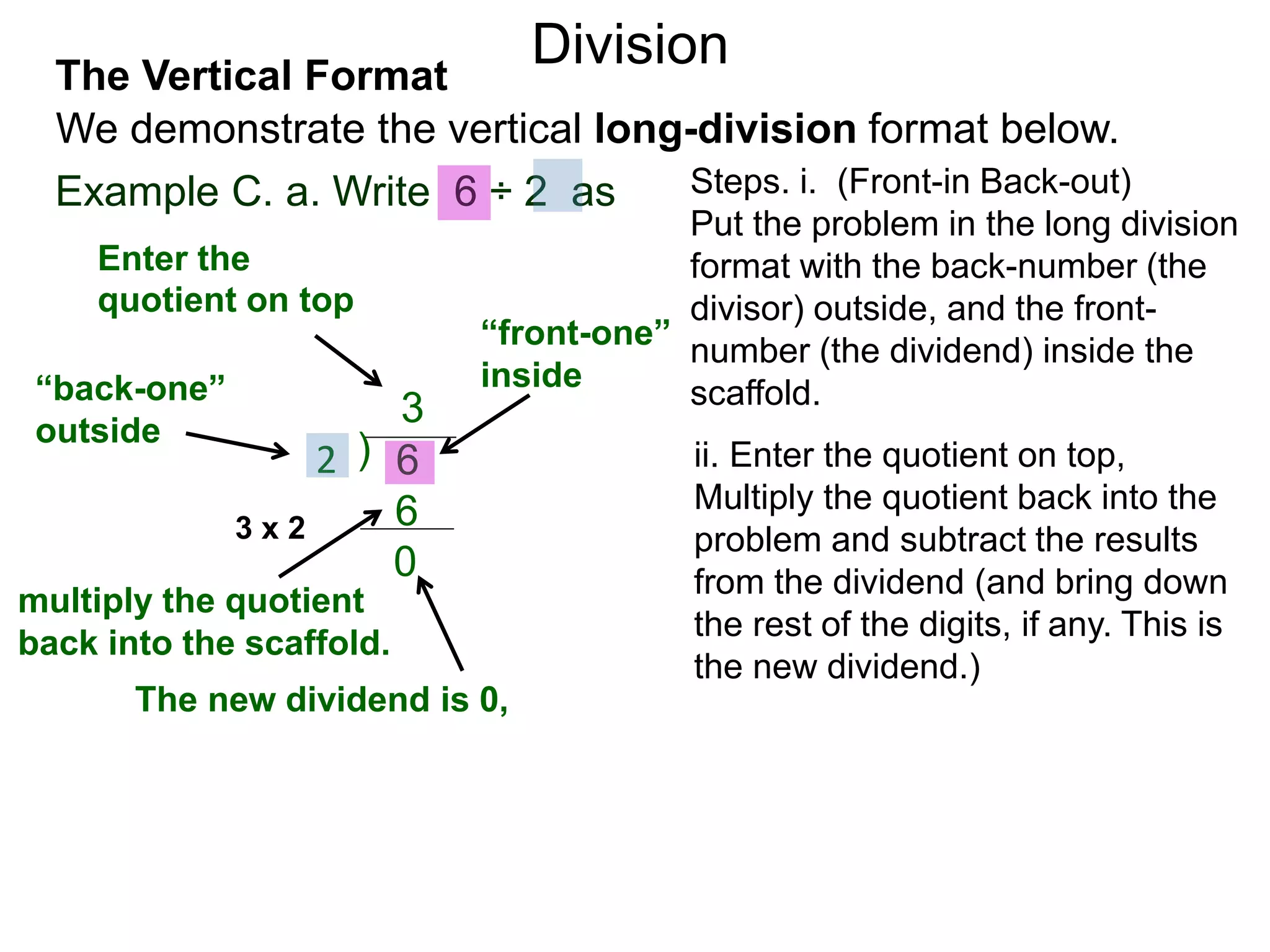
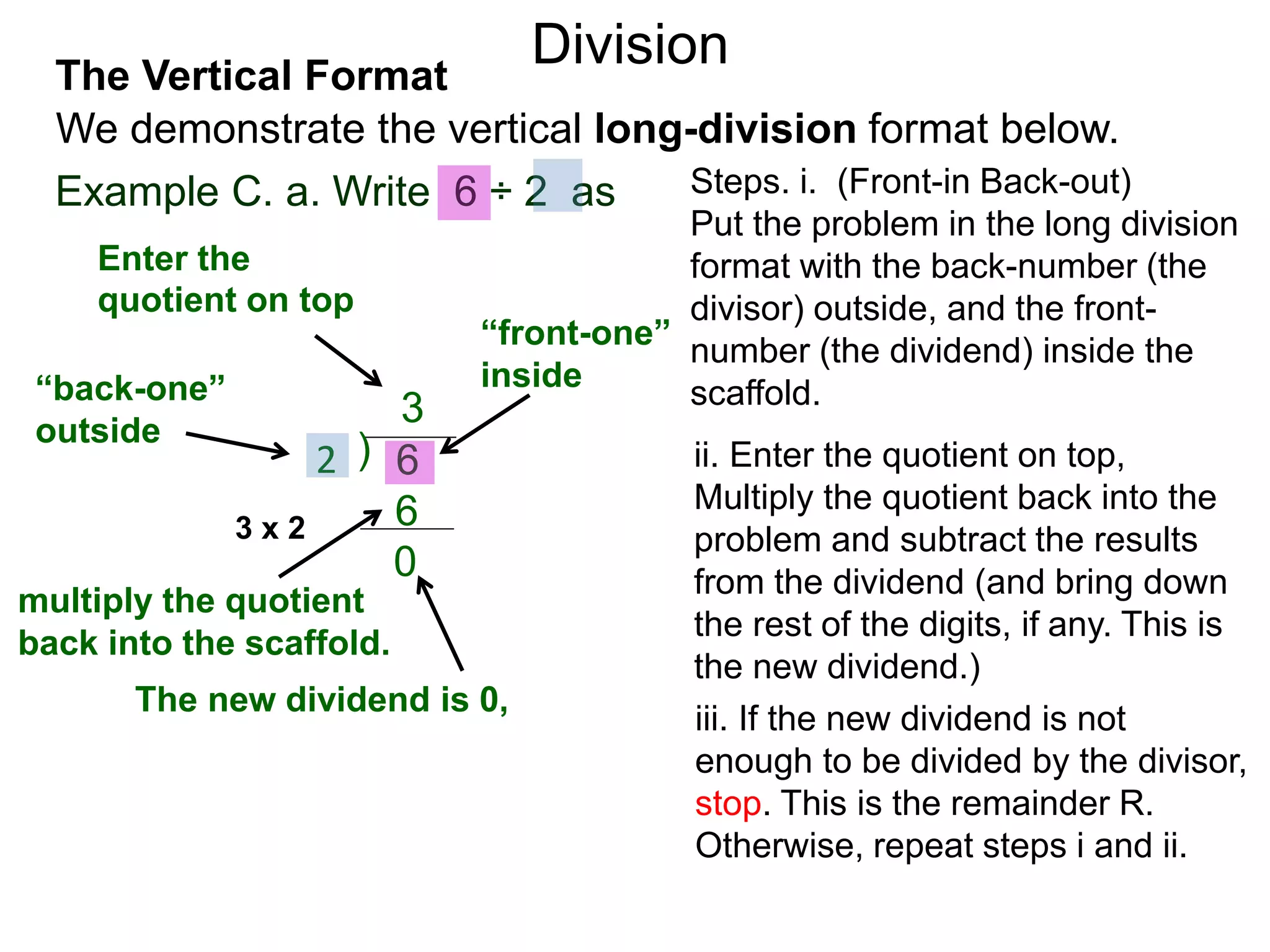
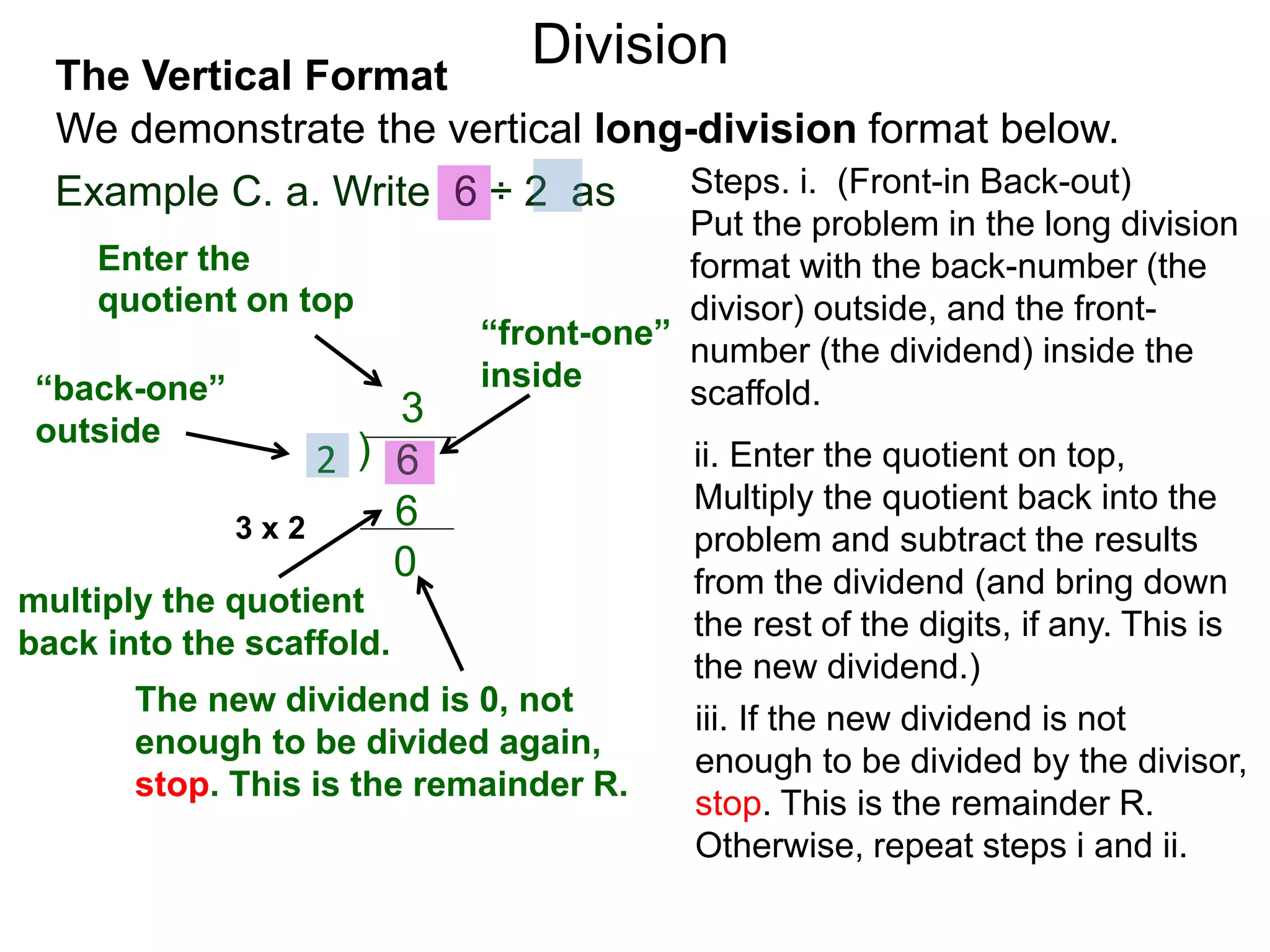
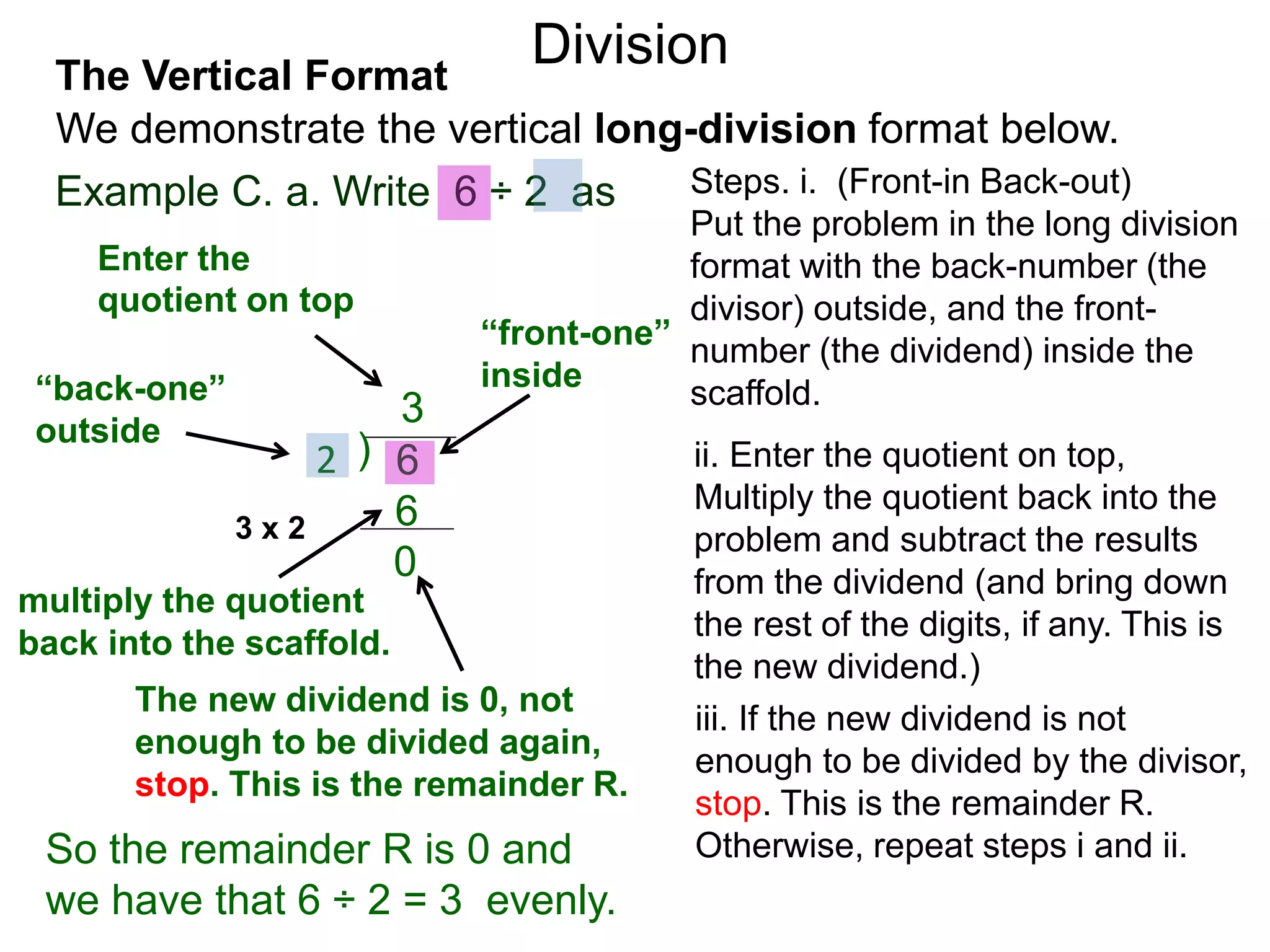
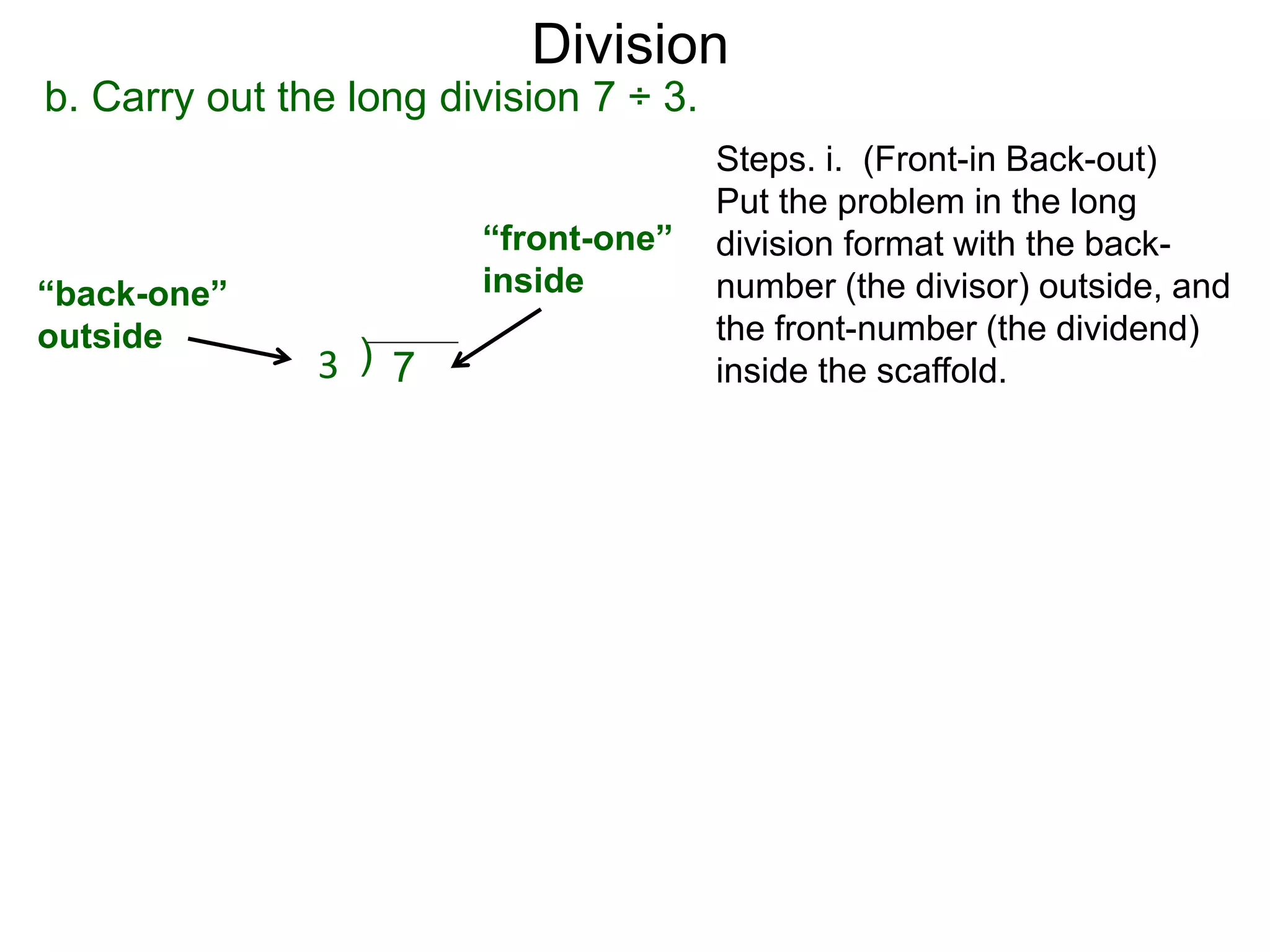
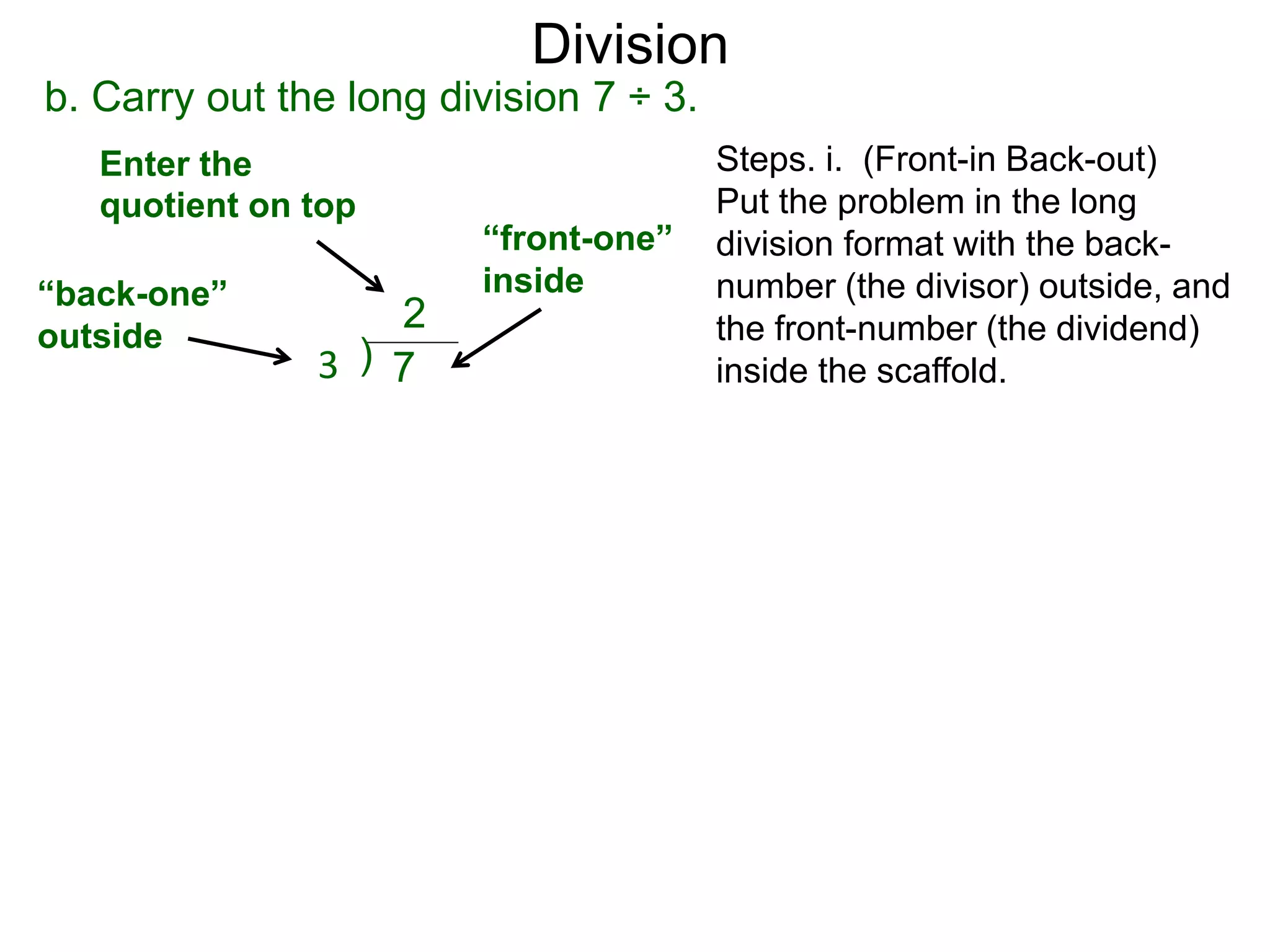
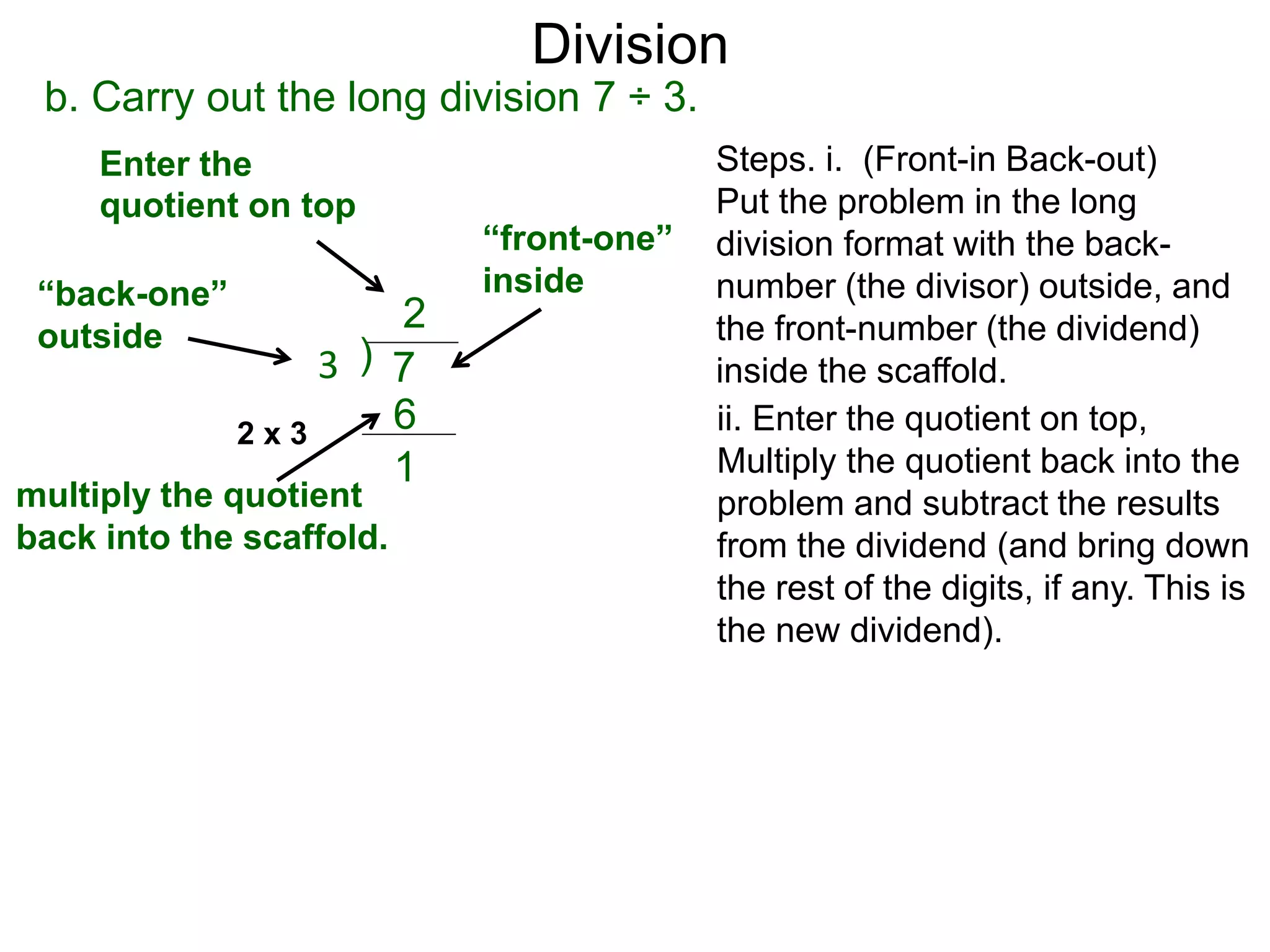
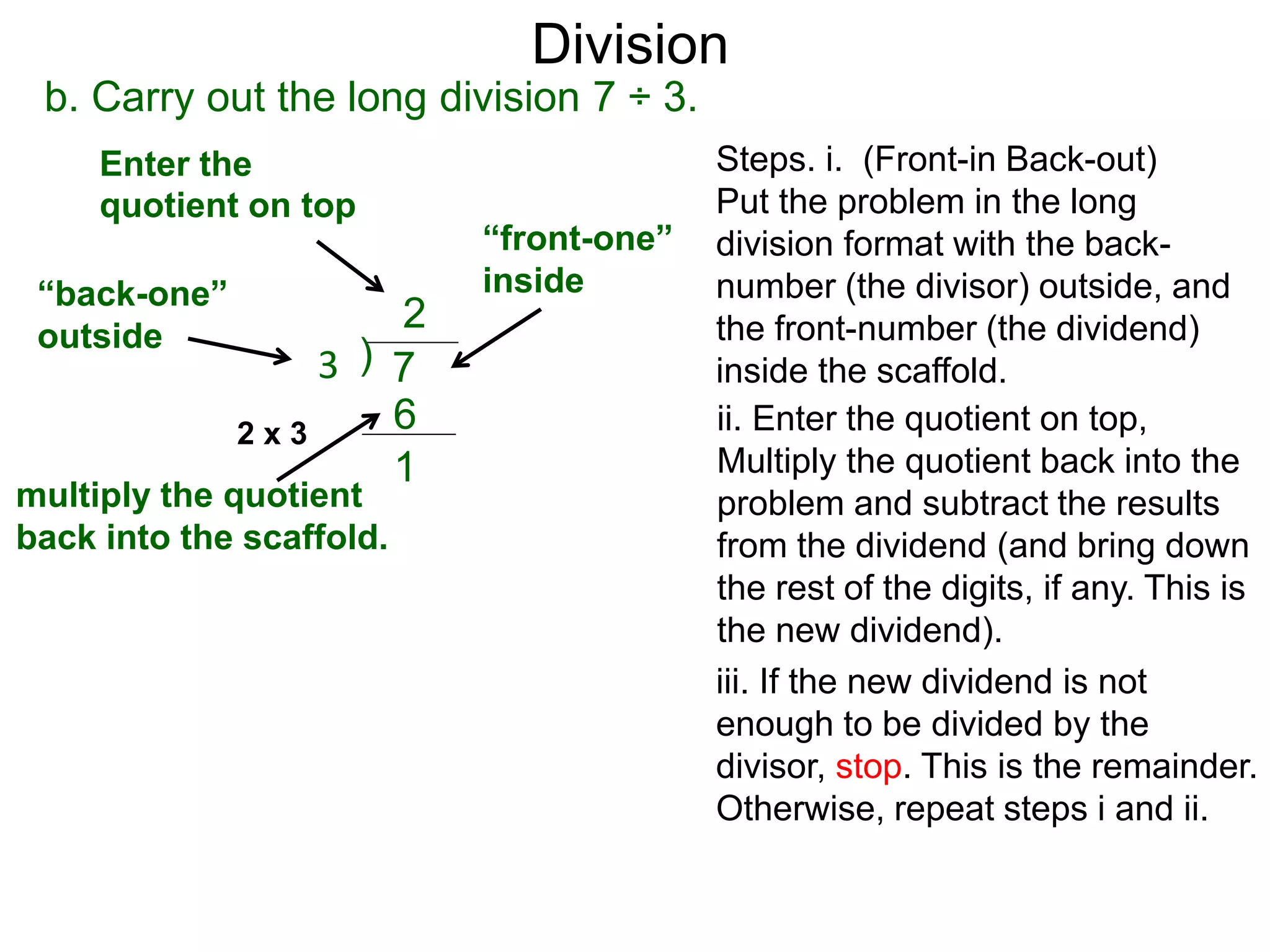
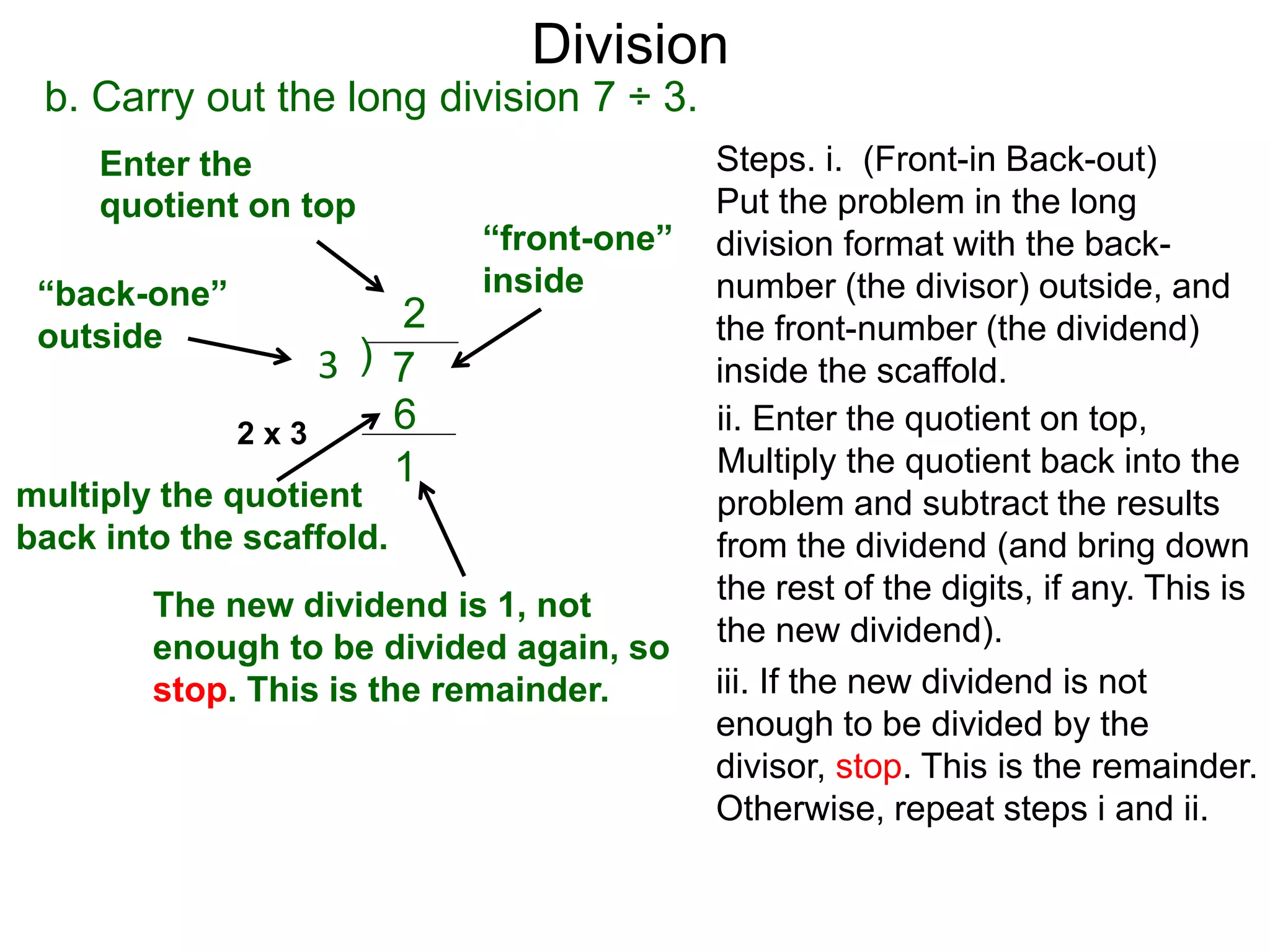
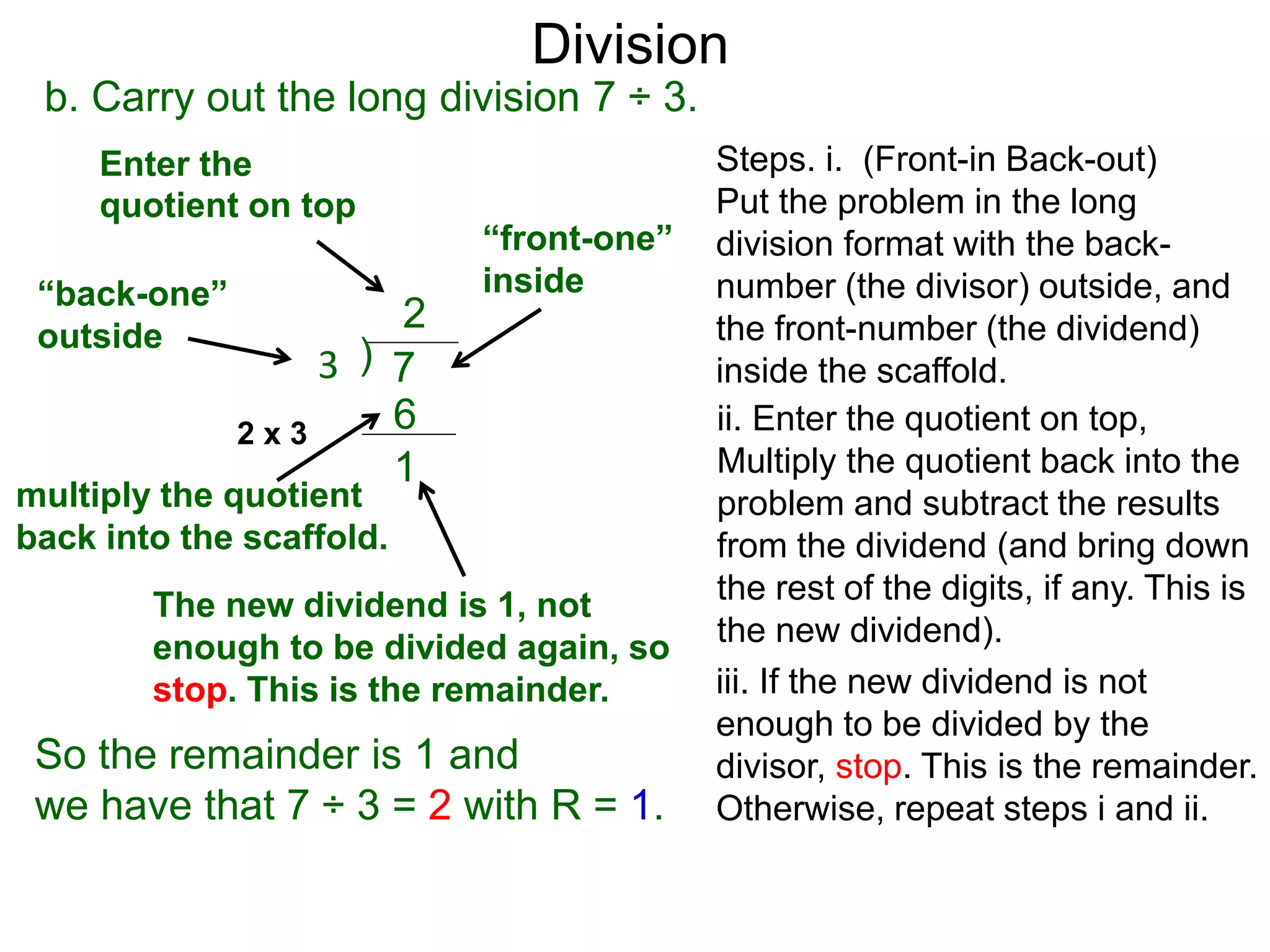
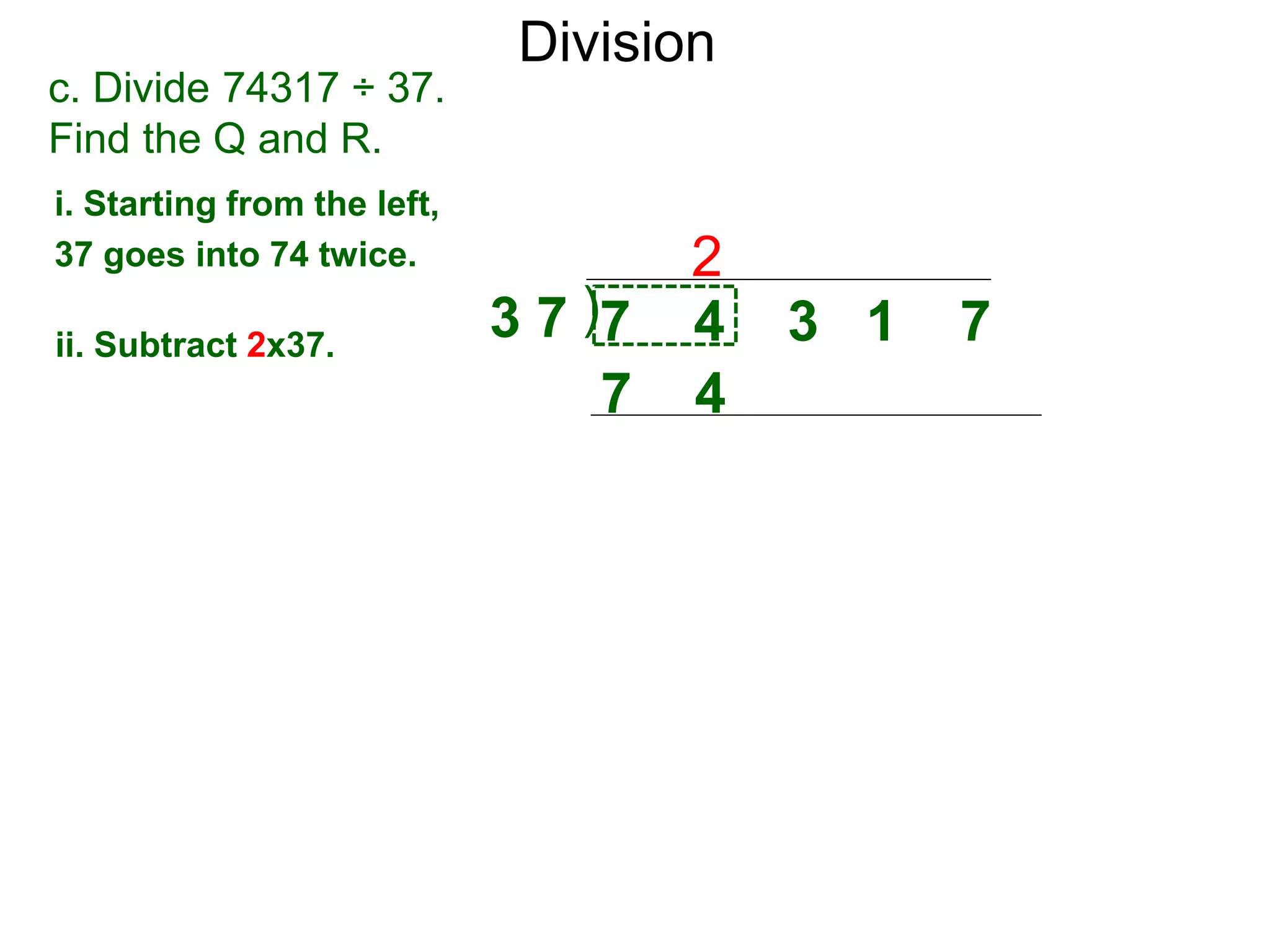
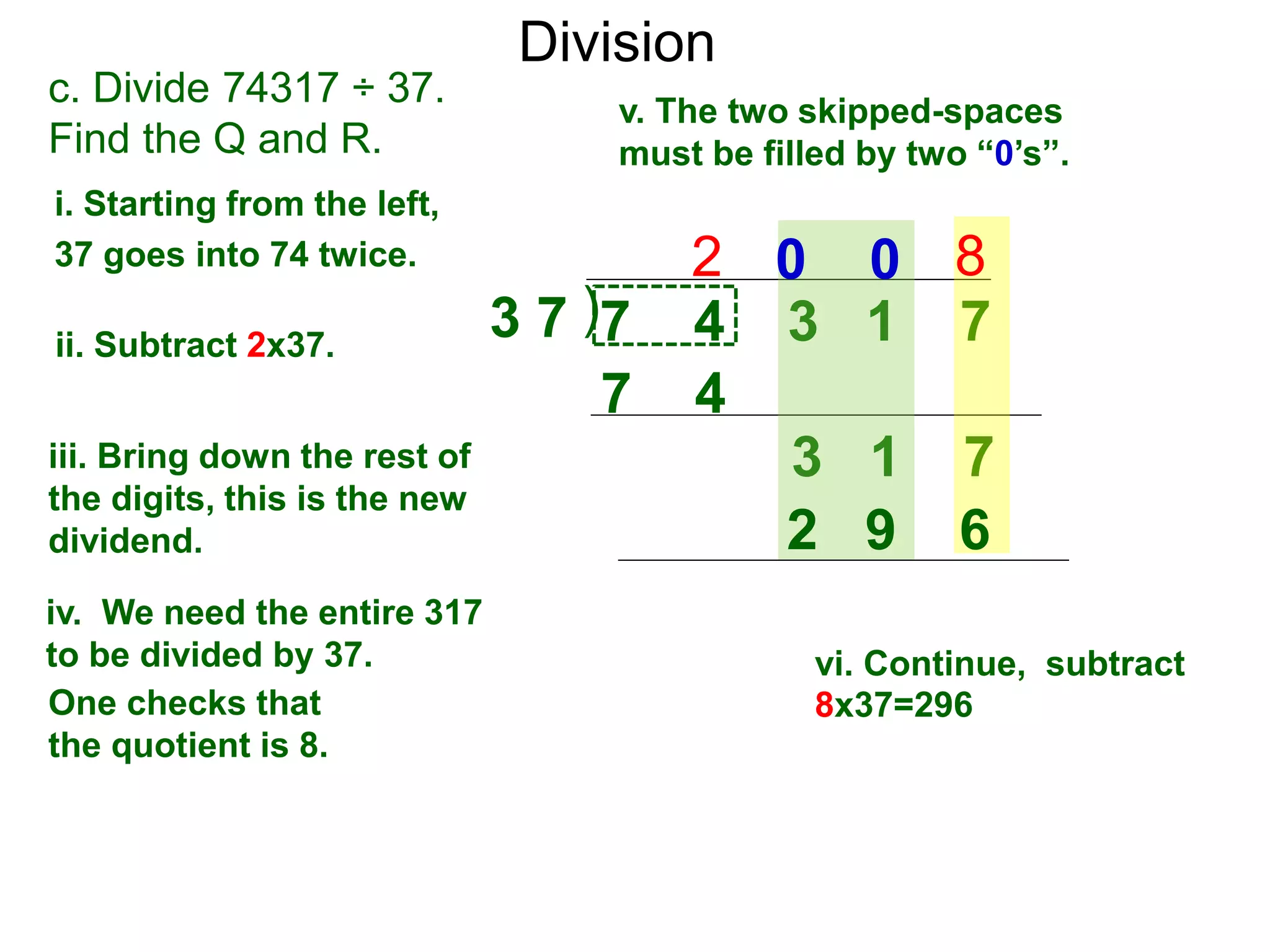
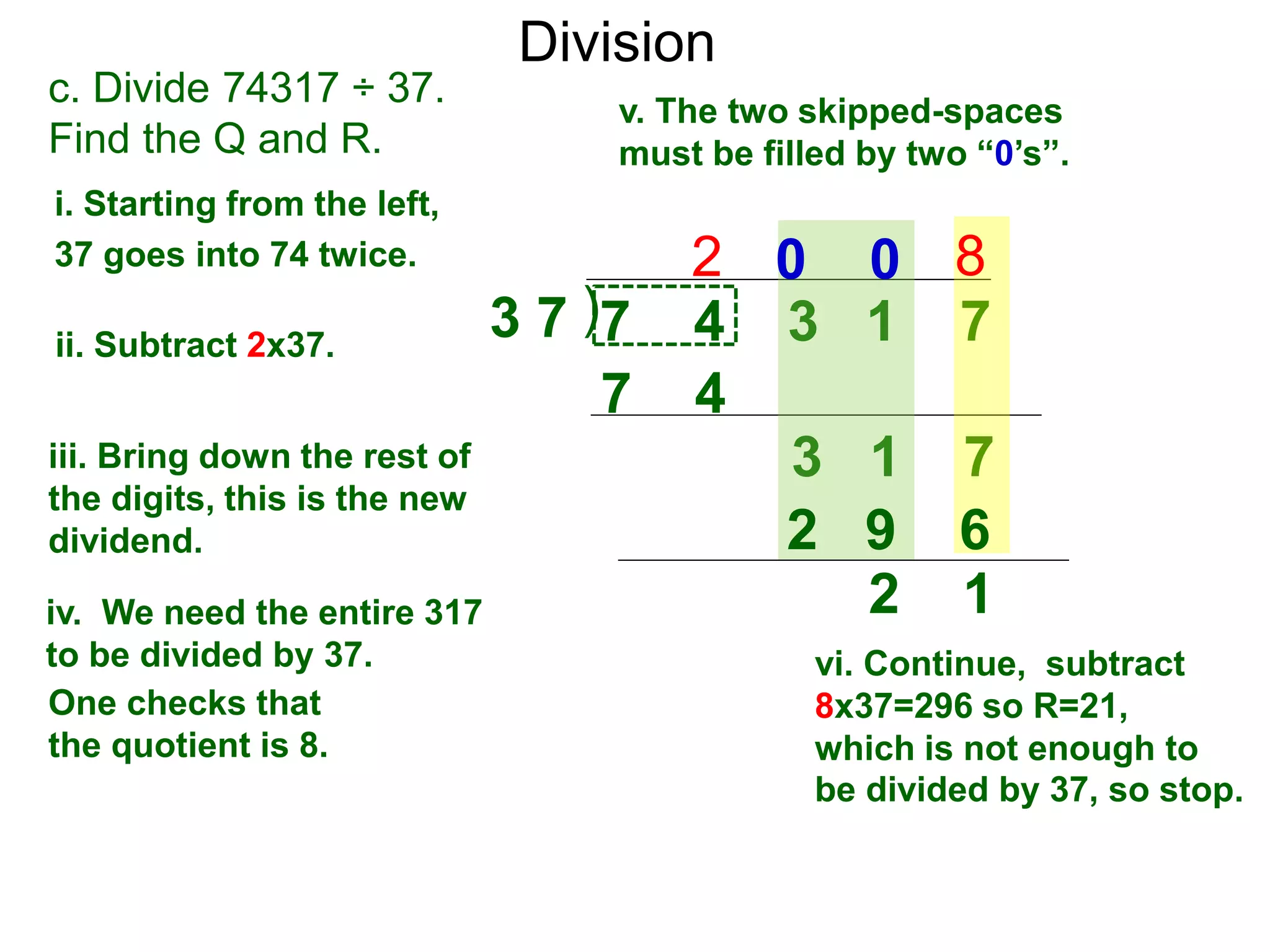
The document discusses addition and subtraction. It defines addition as combining two quantities A and B to obtain a sum S, where A and B are the addends. To add two numbers, one lines them up vertically according to place value and adds the digits from right to left, carrying when necessary. Subtraction is defined as taking away or undoing an addition. To subtract, one lines numbers up vertically and subtracts the digits from right to left, borrowing when needed. Examples of adding and subtracting multi-digit numbers are provided.

1. Addition
Back to Algebra–Ready Review Content.

2. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)

3. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..

4. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).

5. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).

6. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
8,978
657+
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).
1. line up the numbers vertically
to match the place values,

7. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
8,978
657+
2. add the digits from right to left and
“carry” when necessary.
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).
1. line up the numbers vertically
to match the place values,

8. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
8,978
657+
1
5
2. add the digits from right to left and
“carry” when necessary.
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).
1. line up the numbers vertically
to match the place values,

9. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
8,978
657+
1
53
1
2. add the digits from right to left and
“carry” when necessary.
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).
1. line up the numbers vertically
to match the place values,

10. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
8,978
657+
1
53
1
6
1
2. add the digits from right to left and
“carry” when necessary.
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).
1. line up the numbers vertically
to match the place values,

11. Addition
To “add” means to combine two quantities A and B.
The digit–sum table
(Wikipedia)
To add two numbers,
Example A.
Add 8,978 + 657
8,978
657+
1
53
1
6
1
9,So the sum is 9,635.
2. add the digits from right to left and
“carry” when necessary.
The combined result is called the sum or the total of A and B.
All the following words mean to “add”: total, sum, combine,
increase by, count up, aggregate, augmented by, tally, etc..
A, B are called the addends and the sum is often denoted as S
i.e. A + B = S (Sum).
1. line up the numbers vertically
to match the place values,

12. Addition
+

13. Addition
+

14. Addition
+ +

15. Addition
=
+ +

16. If we are to add two apples to a pile of three apples, the outcome
is the same as adding three apples to the pile of two apples.
Addition
+
=
+

17. In general, if A and B are two numbers, then A + B = B + A
and we say that “the addition operation is commutative.”
If we are to add two apples to a pile of three apples, the outcome
is the same as adding three apples to the pile of two apples.
Addition
+
=
+

18. In general, if A and B are two numbers, then A + B = B + A
and we say that “the addition operation is commutative.”
If we are to add two apples to a pile of three apples, the outcome
is the same as adding three apples to the pile of two apples.
Addition
=
The subtraction operation is not commutative, that is,
– –≠
In practical terms, this means that when doing addition,
we don’t care who is added to whom,
or A – B ≠ B – A
but when doing subtraction,
be sure “who” is taken away from “whom.”
+ +

19. Subtraction
To subtract is to take away, or to undo an addition.

20. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.

21. Subtraction
To subtract is to take away, or to undo an addition.
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and we write
A – B = D (for difference).

22. Subtraction
To subtract is to take away, or to undo an addition.
The following phrases are also translated as “A – B”:
“A subtract B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away from A.”
We write “A – B” for taking the amount B away from A.
We call the outcome “the difference of A and B” and we write
A – B = D (for difference).

23. Subtraction
To subtract is to take away, or to undo an addition.
The following phrases are also translated as “A – B”:
“A subtract B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away from A.”
We write “A – B” for taking the amount B away from A.
Hence the statements “five apples take away three apples,”
all mean 5 – 3
“three apples are taken away from five apples,”
“five apples minus three apples,”
= 2 .
We call the outcome “the difference of A and B” and we write
A – B = D (for difference).

24. Subtraction
To subtract is to take away, or to undo an addition.
If “who is taken away from whom” is not specified, then it is
assumed that we are taking the smaller number away from the
bigger one. So “the difference between $10 and $50” is
50 –10 = $40. (In fact, we can’t do 10 – 50, yet.)
The following phrases are also translated as “A – B”:
“A subtract B,” “A minus B,” “A less B,” “A is decreased or
reduced by B,” “B is subtracted, or is taken away from A.”
We write “A – B” for taking the amount B away from A.
Hence the statements “five apples take away three apples,”
all mean 5 – 3
“three apples are taken away from five apples”
“five apples minus three apples,”
= 2 .
We call the outcome “the difference of A and B” and we write
A – B = D (for difference).

25. Subtraction
To subtract,
1. lineup the numbers vertically,

26. Subtraction
To subtract,
1. lineup the numbers vertically,
For example, 634 – 87 is: 6 3 4
8 7–

27. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary.

28. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow

29. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow
14
2
7

30. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow
14
2
7
12
5

31. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow
14
2
7
12
5
45

32. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow
14
2
7
12
5
45
When reading mathematical expressions or translating
real life problems involving subtraction into mathematics,
always ask the question “who subtracts whom?”,
answer it clearly, then proceed.

33. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow
14
2
7
12
5
45
Example A.
The store price of a Thingamajig is $500. How much money
do we save if we buy one for $400 online?
When reading mathematical expressions or translating
real life problems involving subtraction into mathematics,
always ask the question “who subtracts whom?”,
answer it clearly, then proceed.

34. Subtraction
For example, 634 – 87 is: 6 3 4
8 7–
To subtract,
1. lineup the numbers vertically,
2. subtract the digits from right to left and “borrow” when it
is necessary. need to borrow
14
2
7
12
5
45
Example A.
The store price of a Thingamajig is $500. How much money
do we save if we buy one for $400 online?
The amount saved is: the expensive price – the cheaper price,
so we saved 500 – 400 = $100.
When reading mathematical expressions or translating
real life problems involving subtraction into mathematics,
always ask the question “who subtracts whom?”,
answer it clearly, then proceed.

35. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
108th floor
top

36. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
108th floor
top
1st hr
42th floor

37. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
108th floor
top
1st hr
42th floor
2nd hr
67th floor

38. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor

39. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor

40. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.

41. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.

42. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.
Nth fl.
108th fl.

43. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.
Nth fl.
108th fl.
?

44. Subtraction
Example B. We climbed the
108-floor Sears Tower in Chicago.
After 1 hour we were at the 42nd
floor. After two hours, we were at
the 67th floor.
After the 1st hour, we still have 108 – 42 = 66 floors to the top.
a. How many floors were we away
from the top after the 1st hour and
how many floors did we climb during the 2nd hour?
108th floor
top
1st hr
42th floor
2nd hr
67th floor
During the 2nd hour we climbed from the 42nd floor to the 67th
floor hence we climbed 67 – 42 = 25 floors during the 2nd hour.
b. We are on the Nth floor, how many floors are we
from the 108th floor? Write the answer as a subtraction.
We are on the Nth floor out of total 108 floors,
so the number of remaining floors to the top
is “108 – N” as shown. (Not “N – 108”!)
Nth fl.
108th fl.
108 – N

45. We simplify the notation for adding the same quantity
repeatedly.
Multiplication

46. We simplify the notation for adding the same quantity
repeatedly.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
Multiplication

47. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
Multiplication

48. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
Note that 3 copies = 2 copies
so that 3 x 2 = 2 x 3.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
Multiplication

49. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
Note that 3 copies = 2 copies
so that 3 x 2 = 2 x 3.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
In general, just as addition,
Multiplication s commutative, i.e. A x B = B x A.
Multiplication

50. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
Note that 3 copies = 2 copies
so that 3 x 2 = 2 x 3.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
In the expression: 3 x 2 = 2 x 3 = 6
In general, just as addition,
Multiplication s commutative, i.e. A x B = B x A.
Multiplication

51. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
the multiplicands 2 and 3
are called factors (of 6).
Note that 3 copies = 2 copies
so that 3 x 2 = 2 x 3.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
In the expression: 3 x 2 = 2 x 3 = 6
In general, just as addition,
Multiplication s commutative, i.e. A x B = B x A.
Multiplication

52. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
the multiplicands 2 and 3
are called factors (of 6).
the result 6 is
called the product
(of 2 and 3).
Note that 3 copies = 2 copies
so that 3 x 2 = 2 x 3.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
In the expression: 3 x 2 = 2 x 3 = 6
In general, just as addition,
Multiplication s commutative, i.e. A x B = B x A.
Multiplication

53. We simplify the notation for adding the same quantity
repeatedly.
We call this operation multiplication and we say that
“3 times 2 is 6” or “3 multiplied with 2 is 6”.
the multiplicands 2 and 3
are called factors (of 6).
the result 6 is
called the product
(of 2 and 3).
Note that 3 copies = 2 copies
so that 3 x 2 = 2 x 3.
2 + 2 + 2 = 6
3 copies
as 3 x 2 or 3*2 or 3(2) = 6.
For example, we shall write
In the expression: 3 x 2 = 2 x 3 = 6
(Note: 1 and 6 are also factors of 6 because 1 x 6 = 6 x 1 = 6.)
In general, just as addition,
Multiplication s commutative, i.e. A x B = B x A.
Multiplication

54. The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
Multiplication

55. * (0 * x = 0 * x = 0)
The product of zero with any
number is 0.
The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
Multiplication

56. * (0 * x = 0 * x = 0)
The product of zero with any
number is 0.
* (1 * x = x * 1 = x)
The product of 1 with any
number x is x.
The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
Multiplication

57. * For the products with 9 as a factor, the sum of their digits is 9.
* (0 * x = 0 * x = 0)
The product of zero with any
number is 0.
* (1 * x = x * 1 = x)
The product of 1 with any
number x is x.
The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
Multiplication

58. * For the products with 9 as a factor, the sum of their digits is 9.
6 x 9 = 54 7 x 9 = 63 8 x 9 = 72 9 x 9 = 81
For example,
* (0 * x = 0 * x = 0)
The product of zero with any
number is 0.
* (1 * x = x * 1 = x)
The product of 1 with any
number x is x.
The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
all have digit sum equal to 9,
Multiplication

59. * For the products with 9 as a factor, the sum of their digits is 9.
6 x 9 = 54 7 x 9 = 63 8 x 9 = 72 9 x 9 = 81
For example,
i.e. 5 + 4 = 9,
* (0 * x = 0 * x = 0)
The product of zero with any
number is 0.
* (1 * x = x * 1 = x)
The product of 1 with any
number x is x.
The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
all have digit sum equal to 9,
Multiplication

60. * For the products with 9 as a factor, the sum of their digits is 9.
6 x 9 = 54 7 x 9 = 63 8 x 9 = 72 9 x 9 = 81
For example,
i.e. 5 + 4 = 9, 6 + 3 = 9
* (0 * x = 0 * x = 0)
The product of zero with any
number is 0.
* (1 * x = x * 1 = x)
The product of 1 with any
number x is x.
The multiplication table shown
here is to be memorized and
below are some features and
tricks that might help.
7 + 2 = 9, 8 + 1 = 9
all have digit sum equal to 9,
Multiplication

61. * The following 4-digit numbers
represent the products of the
higher digits 6 thru 9, the more
difficult part of the table:
Multiplication

62. 6636 6742 6848 6954
7749 7856 7963
8864 8972
9981
* The following 4-digit numbers
represent the products of the
higher digits 6 thru 9, the more
difficult part of the table:
Multiplication

63. 6636 6742 6848 6954
7749 7856 7963
8864 8972
9981
* The following 4-digit numbers
represent the products of the
higher digits 6 thru 9, the more
difficult part of the table:
6 x 7 = 42 (= 7 x 6)
For example,
7 x 8 = 56 (= 8 x 7).
Multiplication

64. 6636 6742 6848 6954
7749 7856 7963
8864 8972
9981
* The following 4-digit numbers
represent the products of the
higher digits 6 thru 9, the more
difficult part of the table:
6 x 7 = 42 (= 7 x 6)
For example,
The numbers with 2 as a factor: 0, 2, 4, 6, 8,…etc
are called even numbers.
7 x 8 = 56 (= 8 x 7).
Multiplication

65. 6636 6742 6848 6954
7749 7856 7963
8864 8972
9981
* The following 4-digit numbers
represent the products of the
higher digits 6 thru 9, the more
difficult part of the table:
6 x 7 = 42 (= 7 x 6)
For example,
The numbers with 2 as a factor: 0, 2, 4, 6, 8,…etc
are called even numbers.
The numbers 0(= 0*0), 1(= 1*1), 4(= 2*2), 9(= 3*3), 16(= 4*4),..,
of the form x*x, down the diagonal, are called square numbers.
7 x 8 = 56 (= 8 x 7).
Multiplication

66. The Vertical Format
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
Multiplication

67. The Vertical Format
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
Multiplication

68. The Vertical Format
47
7x
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
Multiplication

69. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
7x
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

70. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
7x
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

71. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
7x
8
record
the 8,
carry
the 2
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

72. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
ii. Multiply the next digit of the double
digit number to the single digit,
7x
8
record
the 8,
carry
the 2
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

73. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
ii. Multiply the next digit of the double
digit number to the single digit,
7x
8
record
the 8,
carry
the 2
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28ii. 7x7=49,
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

74. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
ii. Multiply the next digit of the double
digit number to the single digit,
7x
8
record
the 8,
carry
the 2
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28ii. 7x7=49,
49+2=51
add the previous carry to the product,
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

75. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
ii. Multiply the next digit of the double
digit number to the single digit,
7x
8
record
the 8,
carry
the 2
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28ii. 7x7=49,
1
record
the 1,
5
carry
the 5
49+2=51
add the previous carry to the product,
record the unit-digit of this sum and
carry the 10’s digit of this sum.
record the unit-digit of the product,
and carry the 10’s digit of the product.
Multiplication

76. The Vertical Format
47
i. Starting from the right,
multiply the two unit-digits,
ii. Multiply the next digit of the double
digit number to the single digit,
7x
8
record
the 8,
carry
the 2
For example,
We use a vertical format to multiply larger numbers.
The following demonstrates how this is done.
We start with a two-digit number times a single digit number.
i. 4x7=28ii. 7x7=49,
1
record
the 1,
5
carry
the 5
49+2=51
add the previous carry to the product,
record the unit-digit of this sum and
carry the 10’s digit of this sum.
record the unit-digit of the product,
and carry the 10’s digit of the product.
To multiply a longer number against a
single digit number, repeat step ii until
all the digits are multiplied.
Multiplication

77. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
47
7x
9
Multiplication
6

78. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
9For example,
Multiplication
6

79. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=28
9For example,
Multiplication
6

80. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=287x7=49,
49+2=51
9For example,
Multiplication
6

81. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=287x7=49,
1
record
the 1
49+2=51
9For example,
Multiplication
carry
the 5
6

82. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=287x7=49,
1
record
the 1
carry
the 5
49+2=51
9
9x7=63,
63+5= 68
For example,
Multiplication
6

83. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=287x7=49,
1
record
the 1
carry
the 5
49+2=51
9
9x7=63,
63+5= 68
8
record
the 8
carry
the 6
6
For example,
Multiplication
6

84. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=287x7=49,
1
record
the 1
carry
the 5
49+2=51
9
9x7=63,
63+5= 68
8
record
the 8
carry
the 6
6
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Multiplication
6

85. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
47
7x
8
record
the 8
carry
the 2
4x7=287x7=49,
1
record
the 1
carry
the 5
49+2=51
9
9x7=63,
63+5= 68
8
record
the 8
carry
the 6
6
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
Multiplication
6

86. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
1
record
the 1
9
8
record
the 8
carry
the 6
6
6
Multiplication
x

87. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
4x6=24
1
record
the 1
9
8
record
the 8
carry
the 6
6
6
Multiplication
x

88. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
4x6=24
1
record
the 1
←record
9
8
record
the 8
carry
the 6
6
6
carry
the 2
4
Multiplication
x

89. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
4x6=247x6=42,
1
record
the 1
←record
42+2=44
9
8
record
the 8
carry
the 6
6
6
carry
the 2
4
Multiplication
x

90. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
carry
the 4
4x6=247x6=42,
1
record
the 1
←record
42+2=44
9
8
record
the 8
carry
the 6
6
6
carry
the 2
44
Multiplication
x

91. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
carry
the 4
4x6=247x6=42,
1
record
the 1
←record
42+2=44
9
9x6=54
54+4= 58
8
record
the 8
carry
the 6
6
6
carry
the 2
44
Multiplication
x

92. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
carry
the 4
4x6=247x6=42,
1
record
the 1
←record
42+2=44
9
9x6=54
54+4= 58
8
record
the 8
carry
the 6
6
6
carry
the 2
4485
Multiplication
x

93. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
record
the 8
carry
the 4
4x6=247x6=42,
1
record
the 1
←record
42+2=44
9
9x6=54
54+4= 58
8
record
the 8
carry
the 6
6
6
carry
the 2
Finally, we obtain the answer
by adding the two rows.
4485
Multiplication
x

94. We treat the multiplication of two
multiple digit numbers as separate
problems of multiplying with a
single digit number.
we start the multiplication as
before by multiplying the top
with the bottom unit-digit.
When this is completed, we
proceed with the multiplication to
the next digit of the bottom number.
For example,
Because we are in a
place value system, the
result of the multiplication
must be placed in the correct slots,
so it is shift one place to the left.
47
7
8
carry
the 4
4x6=247x6=42,
1
←record
42+2=44
9
9x6=54
54+4= 58
86
6
carry
the 2
Finally, we obtain the answer
by adding the two rows.
4485
8526 5
Multiplication
+
x

95. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
Division

96. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
Division

97. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
Division

98. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
Division

99. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
Division

100. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
Division

101. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
The total T is
the dividend,
Division

102. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
The total T is
the dividend,
The number of parts D
is the divisor.
Division

103. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
The total T is
the dividend,
The number of parts D
is the divisor.
Q is the quotient.
Division

104. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
says that “if T is divided into D equal parts, then each part is Q.”
The total T is
the dividend,
The number of parts D
is the divisor.
Q is the quotient.
Division

105. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
says that “if T is divided into D equal parts, then each part is Q.”
The total T is
the dividend,
The number of parts D
is the divisor.
Q is the quotient.
If T ÷ D = Q then T = D x Q or that D and Q are factors of T,
Division

106. Division is the operation of dividing a given amount into a
prescribed number of equal parts.
For example, if three people share a dozen apples, then each
person gets four apples and there is no leftovers.
In this case, we say that “12 divides evenly by 3”.
We write this as “12 ÷ 3 = 4” which translates into
“if 12 is divided into 3 equal parts, then each part is 4”.
In general, the expression
T ÷ D = Q
says that “if T is divided into D equal parts, then each part is Q.”
The total T is
the dividend,
The number of parts D
is the divisor.
Q is the quotient.
If T ÷ D = Q then T = D x Q or that D and Q are factors of T,
e.g. 12 ÷ 3 = 4 so 12 = 3(4), so both 3 and 4 are factors of 12.
Division

107. The Vertical Format
Division

108. We demonstrate the vertical long-division format below.
The Vertical Format
Division

109. We demonstrate the vertical long-division format below.
The Vertical Format
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.
Division

110. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Division

111. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Division

112. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
Division

113. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend.)
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
Division

114. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend.)
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
multiply the quotient
back into the scaffold.
63 x 2
Division

115. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend.)
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
multiply the quotient
back into the scaffold.
63 x 2
0
The new dividend is 0,
Division

116. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend.)
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
iii. If the new dividend is not
enough to be divided by the divisor,
stop. This is the remainder R.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
63 x 2
0
The new dividend is 0,
Division

117. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend.)
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
iii. If the new dividend is not
enough to be divided by the divisor,
stop. This is the remainder R.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
63 x 2
0
The new dividend is 0, not
enough to be divided again,
stop. This is the remainder R.
Division

118. We demonstrate the vertical long-division format below.
The Vertical Format
Example C. a. Write 6 ÷ 2 as
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend.)
Steps. i. (Front-in Back-out)
Put the problem in the long division
format with the back-number (the
divisor) outside, and the front-
number (the dividend) inside the
scaffold.“back-one”
outside
)2 6
“front-one”
inside
Enter the
quotient on top
3
iii. If the new dividend is not
enough to be divided by the divisor,
stop. This is the remainder R.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
63 x 2
0
The new dividend is 0, not
enough to be divided again,
stop. This is the remainder R.
So the remainder R is 0 and
we have that 6 ÷ 2 = 3 evenly.
Division

119. b. Carry out the long division 7 ÷ 3.
Division

120. b. Carry out the long division 7 ÷ 3.
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
Division

121. b. Carry out the long division 7 ÷ 3.
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Division

122. b. Carry out the long division 7 ÷ 3.
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Enter the
quotient on top
2
Division

123. b. Carry out the long division 7 ÷ 3.
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend).
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Division
Enter the
quotient on top
2

124. b. Carry out the long division 7 ÷ 3.
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend).
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Enter the
quotient on top
2
multiply the quotient
back into the scaffold.
62 x 3
1
Division

125. b. Carry out the long division 7 ÷ 3.
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend).
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Enter the
quotient on top
2
iii. If the new dividend is not
enough to be divided by the
divisor, stop. This is the remainder.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
62 x 3
1
Division

126. b. Carry out the long division 7 ÷ 3.
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend).
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Enter the
quotient on top
2
iii. If the new dividend is not
enough to be divided by the
divisor, stop. This is the remainder.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
62 x 3
1
The new dividend is 1, not
enough to be divided again, so
stop. This is the remainder.
Division

127. b. Carry out the long division 7 ÷ 3.
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend).
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Enter the
quotient on top
2
iii. If the new dividend is not
enough to be divided by the
divisor, stop. This is the remainder.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
62 x 3
1
The new dividend is 1, not
enough to be divided again, so
stop. This is the remainder.
So the remainder is 1 and
we have that 7 ÷ 3 = 2 with R = 1.
Division

128. b. Carry out the long division 7 ÷ 3.
ii. Enter the quotient on top,
Multiply the quotient back into the
problem and subtract the results
from the dividend (and bring down
the rest of the digits, if any. This is
the new dividend).
Steps. i. (Front-in Back-out)
Put the problem in the long
division format with the back-
number (the divisor) outside, and
the front-number (the dividend)
inside the scaffold.
“back-one”
outside
)3 7
“front-one”
inside
Enter the
quotient on top
2
iii. If the new dividend is not
enough to be divided by the
divisor, stop. This is the remainder.
Otherwise, repeat steps i and ii.
multiply the quotient
back into the scaffold.
62 x 3
1
The new dividend is 1, not
enough to be divided again, so
stop. This is the remainder.
So the remainder is 1 and
we have that 7 ÷ 3 = 2 with R = 1.
Put the result in the multiplicative form, we have that
7 = 2 x 3 + 1.
Division

129. Division
)3 7 7 4 3 1 7
c. Divide 74317 ÷ 37.
Find the Q and R.

130. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice. 2
c. Divide 74317 ÷ 37.
Find the Q and R.

131. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
2
c. Divide 74317 ÷ 37.
Find the Q and R.
7 4

132. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
2
c. Divide 74317 ÷ 37.
Find the Q and R.
7 4

133. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
2
c. Divide 74317 ÷ 37.
Find the Q and R.
iv. We need the entire 317
to be divided by 37.
7 4

134. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
2
c. Divide 74317 ÷ 37.
Find the Q and R.
iv. We need the entire 317
to be divided by 37.
v. The two skipped-spaces
must be filled by two “0’s”.
7 4
0 0

135. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
2
c. Divide 74317 ÷ 37.
Find the Q and R.
iv. We need the entire 317
to be divided by 37.
v. The two skipped-spaces
must be filled by two “0’s”.
7 4
80 0
One checks that
the quotient is 8.

136. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
vi. Continue, subtract
8x37=296
2
c. Divide 74317 ÷ 37.
Find the Q and R.
iv. We need the entire 317
to be divided by 37.
v. The two skipped-spaces
must be filled by two “0’s”.
7 4
80 0
2 9 6
One checks that
the quotient is 8.

137. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
vi. Continue, subtract
8x37=296 so R=21,
which is not enough to
be divided by 37, so stop.
2
c. Divide 74317 ÷ 37.
Find the Q and R.
iv. We need the entire 317
to be divided by 37.
v. The two skipped-spaces
must be filled by two “0’s”.
7 4
80 0
2 9 6
2 1
One checks that
the quotient is 8.

138. Division
)3 7 7 4 3 1 7
i. Starting from the left,
37 goes into 74 twice.
ii. Subtract 2x37.
3 1 7iii. Bring down the rest of
the digits, this is the new
dividend.
vi. Continue, subtract
8x37=296 so R=21,
which is not enough to
be divided by 37, so stop.
2
Hence 74317 ÷ 37 = 2008 with R = 21,
or that 74317 = 2008(37) + 21.
c. Divide 74317 ÷ 37.
Find the Q and R.
iv. We need the entire 317
to be divided by 37.
v. The two skipped-spaces
must be filled by two “0’s”.
7 4
80 0
2 9 6
2 1
One checks that
the quotient is 8.