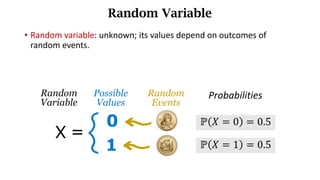
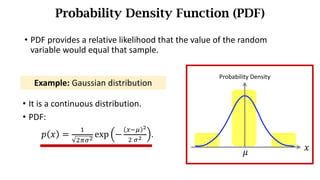
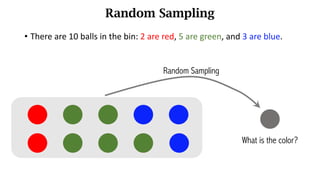
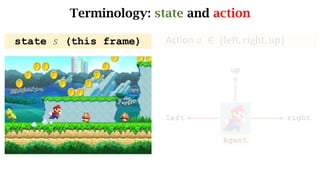
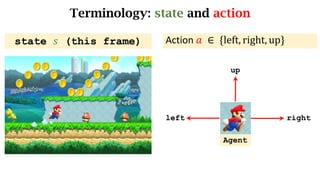
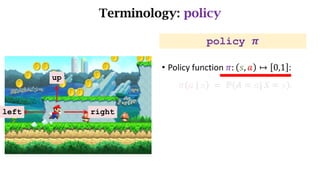
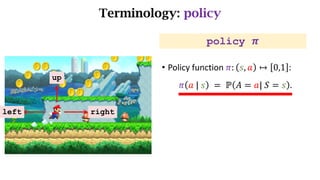
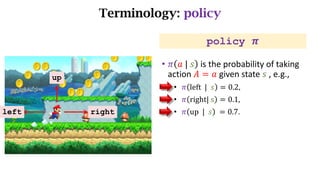
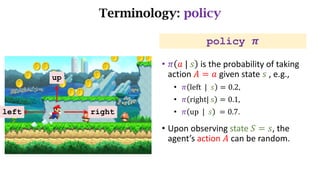
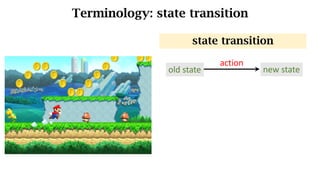
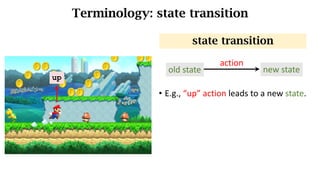
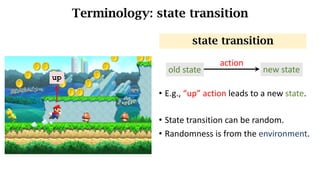
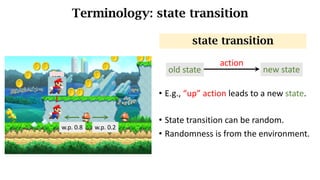
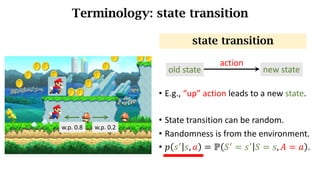
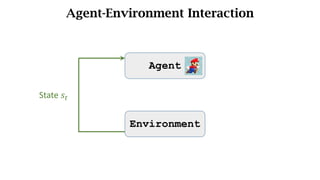
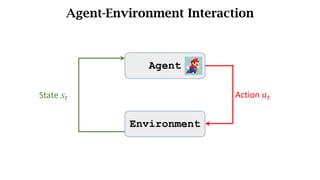
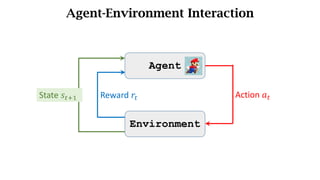
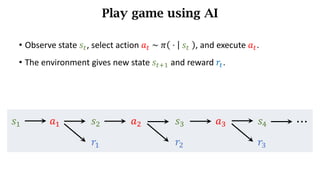
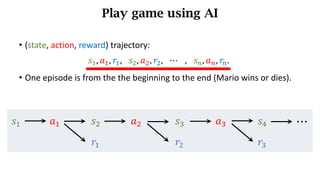
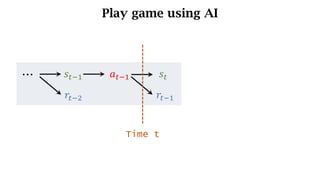
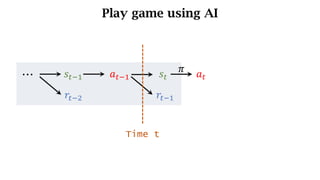
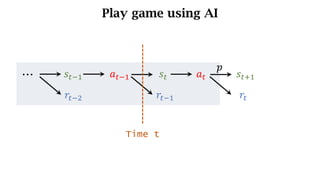
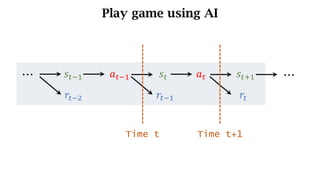
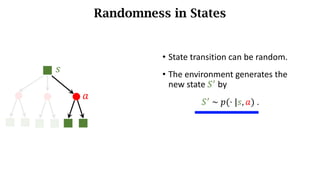
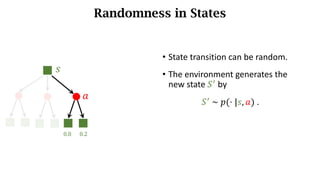
The document provides an introduction to basic concepts in reinforcement learning including: - Random variables and their probability distributions like the probability density function (PDF) and probability mass function (PMF). - The interaction between an agent and its environment including states, actions, policies, rewards, and state transitions. - Sources of randomness from the policy and environment. - The concept of returns which aggregate future rewards with discounts to account for their declining importance.

1. Reinforcement Learning Basics
Shusen Wang
Stevens Institute of Technology
http://wangshusen.github.io/

2. A little bit probability theory…

3. • Random variable: unknown; its values depend on outcomes of
random events.
Random Variable
0
1
X =
Random Possible Random
Variable Val es E ents
Probabilities
ℙ 𝑋 = 0 = 0.5
ℙ 𝑋 = 1 = 0.5

4. • Random variable: unknown; its values depend on outcomes of
random events.
• Uppercase letter 𝑋 for a random variable.
• Lowercase letter 𝑥 for an observed value.
• For example, I flipped a coin 4 times and observed:
• 𝑥) = 1,
• 𝑥* = 1,
• 𝑥+ = 0,
• 𝑥, = 1.
Random Variable

5. • PDF provides a relative likelihood that the value of the random
variable would equal that sample.
Probability Density Function (PDF)

6. • PDF provides a relative likelihood that the value of the random
variable would equal that sample.
Probability Density Function (PDF)
• It is a continuous distribution.
• PDF:
𝑝 𝑥 =
)
*./0
exp −
678 0
* /0 .
Example: Gaussian distribution
Probability Density
𝑥
𝜇

7. • PMF is a function that gives the probability that a discrete random
variable is exactly equal to some value.
Probability Mass Function (PMF)

8. • PMF is a function that gives the probability that a discrete random
variable is exactly equal to some value.
Probability Mass Function (PMF)
• Discrete random variable: 𝑋 ∈ 1, 3, 7 .
• PDF:
𝑝 1 = 0.2,
𝑝 3 = 0.5,
𝑝 7 = 0.3.
Example
1 7
𝑥
Probability Mass
3
0.2
0.5
0.3

9. • PMF is a function that gives the probability that a discrete random
variable is exactly equal to some value.
Probability Mass Function (PMF)
• Discrete random variable: 𝑋 ∈ 1, 3, 7 .
• PDF:
𝑝 1 = 0.2,
𝑝 3 = 0.5,
𝑝 7 = 0.3.
Example
1 7
𝑥
3
0.2
0.5
0.3
Probability Mass

10. Properties of PDF/PMF
• Random variable 𝑋 is in the domain 𝒳.
• For continuous distributions,
∫ 𝑝 𝑥 𝑑𝑥
𝒳
= 1.
• For discrete distributions,
∑ 𝑝 𝑥
6∈𝒳 = 1.

11. • Random variable 𝑋 is in the domain 𝒳.
• For continuous distributions, the expectation of 𝑓(𝑋) is:
𝔼 𝑓 𝑋 = ∫ 𝑝 𝑥 ⋅ 𝑓 𝑥 𝑑𝑥
𝒳
.
• For discrete distributions, the expectation of 𝑓(𝑋) is:
𝔼 𝑓 𝑋 = ∑ 𝑝 𝑥
6∈𝒳 ⋅ 𝑓 𝑥 .
Expectation

12. • There are 10 balls in the bin: 2 are red, 5 are green, and 3 are blue.
Random Sampling
Random Sampling
What is the color?

13. Random Sampling
• Sample red ball w.p. 0.2, green ball w.p. 0.5, and blue ball w.p. 0.3.

14. Random Sampling
• Sample red ball w.p. 0.2, green ball w.p. 0.5, and blue ball w.p. 0.3.

15. Terminologies

16. Terminology: state and action
state 𝑠 (this frame) Action 𝑎 ∈ {left, right, up}
left right
up
Agent

17. Terminology: state and action
state 𝑠 (this frame) Action 𝑎 ∈ {left, right, up}
left right
up
Agent

18. Terminology: policy
left right
up
policy 𝝅
• Policy function 𝜋: 𝑠, 𝑎 ↦ 0,1 :
𝜋 𝑎 | 𝑠 = ℙ 𝐴 = 𝑎| 𝑆 = 𝑠 .

19. Terminology: policy
left right
up
policy 𝝅
• Policy function 𝜋: 𝑠, 𝑎 ↦ 0,1 :
𝜋 𝑎 | 𝑠 = ℙ 𝐴 = 𝑎| 𝑆 = 𝑠 .

20. Terminology: policy
left right
up
• Policy function 𝜋: 𝑠, 𝑎 ↦ 0,1 :
𝜋 𝑎 | 𝑠 = ℙ 𝐴 = 𝑎| 𝑆 = 𝑠 .
policy 𝝅

21. Terminology: policy
left right
up
• 𝜋 𝑎 | 𝑠 is the probability of taking
action 𝐴 = 𝑎 given state 𝑠 , e.g.,
• 𝜋 left | 𝑠 = 0.2,
• 𝜋 right| s = 0.1,
• 𝜋 up | 𝑠 = 0.7.
policy 𝝅

22. Terminology: policy
left right
up
policy 𝝅
• 𝜋 𝑎 | 𝑠 is the probability of taking
action 𝐴 = 𝑎 given state 𝑠 , e.g.,
• 𝜋 left | 𝑠 = 0.2,
• 𝜋 right| s = 0.1,
• 𝜋 up | 𝑠 = 0.7.
• Upon observing state 𝑆 = 𝑠, the
agent’s action 𝐴 can be random.

23. Terminology: policy
left right
up
Random or deterministic policy?

24. Terminology: reward
• Collect a coin: 𝑅 = +1
reward 𝑅

25. Terminology: reward
reward 𝑅
• Collect a coin: 𝑅 = +1
• Win the game: 𝑅 = +10000

26. Terminology: reward
reward 𝑅
• Collect a coin: 𝑅 = +1
• Win the game: 𝑅 = +10000
• Touch a Goomba: 𝑅 = −10000
(game over).

27. Terminology: reward
• Collect a coin: 𝑅 = +1
• Win the game: 𝑅 = +10000
• Touch a Goomba: 𝑅 = −10000
(game over).
• Nothing happens: 𝑅 = 0
reward 𝑅

28. Terminology: state transition
state transition
old state new state
action

29. Terminology: state transition
• E.g., “up” action leads to a new state.
state transition
up
old state new state
action

30. Terminology: state transition
• E.g., “up” action leads to a new state.
• State transition can be random.
• Randomness is from the environment.
state transition
up
old state new state
action

31. Terminology: state transition
• E.g., “up” action leads to a new state.
• State transition can be random.
• Randomness is from the environment.
state transition
up
w.p. 0.8 w.p. 0.2
old state new state
action

32. Terminology: state transition
• E.g., “up” action leads to a new state.
• State transition can be random.
• Randomness is from the environment.
• 𝑝 𝑠_
𝑠, 𝑎 = ℙ 𝑆_
= 𝑠_
𝑆 = 𝑠, 𝐴 = 𝑎 .
state transition
w.p. 0.8 w.p. 0.2
old state new state
action

33. Two Sources of Randomness

34. 𝑠
left
0.2
right
0.1
up
0.7
Randomness in Actions

35. 𝑠
𝐴~𝜋(⋅ |𝑠)
Given state 𝑠, the action can be
random, e.g., .
• 𝜋 “left” 𝑠 = 0.2,
• 𝜋 “right” 𝑠 = 0.1,
• 𝜋 “up” 𝑠 = 0.7.
left
0.2
right
0.1
up
0.7
Randomness in Actions

36. Randomness in States
𝑠
𝑎
• State transition can be random.
• The environment generates the
new state 𝑆_
by
𝑆_
~ 𝑝(⋅ |𝑠, 𝑎) .

37. Randomness in States
𝑠
𝑎
0.8 0.2
• State transition can be random.
• The environment generates the
new state 𝑆_
by
𝑆_
~ 𝑝(⋅ |𝑠, 𝑎) .

38. • The randomness in action is from the policy function:
𝐴 ~ 𝜋 ⋅ 𝑠 .
• The randomness in state is from the state-transition function:
𝑆_
~ 𝑝 ⋅ 𝑠, 𝑎 ) .
Two Sources of Randomness

39. Agent-Environment Interaction

40. Agent-Environment Interaction
Environment
State 𝑠d
Agent

41. Agent-Environment Interaction
Environment
Action 𝑎d
State 𝑠d
Agent

42. State 𝑠d
Agent-Environment Interaction
Environment
Agent
Action 𝑎d
Reward 𝑟d
State 𝑠df)

43. Play game using AI
• Observe state 𝑠d, select action 𝑎d ~ 𝜋 ⋅ 𝑠d , and execute 𝑎d.
• The environment gives new state 𝑠df) and reward 𝑟d.

44. Play game using AI
𝑠) 𝑎) 𝑠*
• Observe state 𝑠d, select action 𝑎d ~ 𝜋 ⋅ 𝑠d , and execute 𝑎d.
• The environment gives new state 𝑠df) and reward 𝑟d.
𝑟)

45. Play game using AI
𝑠) 𝑎) 𝑠* 𝑎* 𝑠+ 𝑎+ 𝑠,
𝑟) 𝑟* 𝑟+
⋯
• Observe state 𝑠d, select action 𝑎d ~ 𝜋 ⋅ 𝑠d , and execute 𝑎d.
• The environment gives new state 𝑠df) and reward 𝑟d.

46. Play game using AI
𝑠) 𝑎) 𝑠* 𝑎* 𝑠+ 𝑎+ 𝑠,
𝑟) 𝑟* 𝑟+
⋯
• (state, action, reward) trajectory:
𝑠), 𝑎), 𝑟), 𝑠*, 𝑎*, 𝑟*, ⋯ , 𝑠h, 𝑎h, 𝑟h.
• One episode is from the the beginning to the end (Mario wins or dies).

47. Play game using AI
• (state, action, reward) trajectory:
𝑠), 𝑎), 𝑟), 𝑠*, 𝑎*, 𝑟*, ⋯ , 𝑠h, 𝑎h, 𝑟h.
• One episode is from the the beginning to the end (Mario wins or dies).
• What is a good policy?
• A good policy leads to big cumulative reward: ∑ 𝛾d7)
⋅ 𝑟d
h
dj) .
• Use the rewards to guide the learning of policy.

48. Rewards and Returns

49. Return
• 𝑈d = 𝑅d + 𝑅df) + 𝑅df* + 𝑅df+ + ⋯
Definition: Return (aka cumulative future reward).

50. Return
• 𝑈d = 𝑅d + 𝑅df) + 𝑅df* + 𝑅df+ + ⋯
Definition: Return (aka cumulative future reward).
Question: At time 𝑡, are 𝑅d and 𝑅df) equally important?
• Which of the followings do you prefer?
• I give you $100 right now.
• I will give you $100 one year later.

51. Return
• 𝑈d = 𝑅d + 𝑅df) + 𝑅df* + 𝑅df+ + ⋯
Definition: Return (aka cumulative future reward).
Question: At time 𝑡, are 𝑅d and 𝑅df) equally important?
• Which of the followings do you prefer?
• I give you $80 right now.
• I will give you $100 one year later.

52. Return
• 𝑈d = 𝑅d + 𝑅df) + 𝑅df* + 𝑅df+ + ⋯
Definition: Return (aka cumulative future reward).
Question: At time 𝑡, are 𝑅d and 𝑅df) equally important?
• Which of the followings do you prefer?
• I give you $80 right now.
• I will give you $100 one year later.
• Future reward is less valuable than present reward.
• 𝑅df) should be given less weight than 𝑅d.

53. Discounted Returns
• 𝑈d = 𝑅d + 𝑅df) + 𝑅df* + 𝑅df+ + ⋯
Definition: Return (aka cumulative future reward).
• 𝛾: discount factor (tuning hyper-parameter).
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + 𝛾+
𝑅df+ + ⋯
Definition: Discounted return (aka cumulative discounted future reward).

54. Discounted Returns
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return (at time 𝑡).

55. Randomness in Returns
At the end of the game, we observe 𝑢d.
Definition: Discounted return (at time 𝑡).
• We observe all the rewards, 𝑟d, 𝑟df), 𝑟df*, ⋯ , 𝑟h.
• We thereby know the discounted return:
𝑢d = 𝑟d + 𝛾 𝑟df) + 𝛾*
𝑟df* + ⋯ + 𝛾h7d
𝑟h.
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.

56. Randomness in Returns
At time 𝑡, the rewards, 𝑅d, ⋯ , 𝑅h, are random, so the return 𝑈d is random.
Definition: Discounted return (at time 𝑡).
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.

57. Randomness in Returns
At time 𝑡, the rewards, 𝑅d, ⋯ , 𝑅h, are random, so the return 𝑈d is random.
Definition: Discounted return (at time 𝑡).
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
• Reward 𝑅n depends on 𝑆n and 𝐴n.
• States can be random: 𝑆n ∼ 𝑝 ⋅ 𝑠n7), 𝑎n7) .
• Actions can be random: 𝐴n ∼ 𝜋 ⋅ 𝑠n .
• If either 𝑆n or 𝐴n is random, then 𝑅n is random.

58. Randomness in Returns
At time 𝑡, the rewards, 𝑅d, ⋯ , 𝑅h, are random, so the return 𝑈d is random.
Definition: Discounted return (at time 𝑡).
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
• Reward 𝑅n depends on 𝑆n and 𝐴n.
• 𝑈d depends on 𝑅d, 𝑅df), ⋯ , 𝑅h.
• è 𝑈d depends on 𝑆d, 𝐴d, 𝑆df), 𝐴df), ⋯ , 𝑆h, 𝐴h.

59. Randomness in Returns
Time
Time t End

60. Randomness in Returns
Time
Time t End
𝑅d 𝑅df) 𝑅df* 𝑅h
⋯
𝑈d is a random variable

61. Randomness in Returns
Time
Time t End
𝑟d 𝑟df) 𝑟df* 𝑟h
⋯
𝑢d is an observed value

62. Value Functions

63. Action-Value Function 𝑄. 𝑠, 𝑎
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.

64. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.

65. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
𝑈d depends on states 𝑆d, 𝑆df), ⋯ , 𝑆h and actions 𝐴d, 𝐴df), ⋯ , 𝐴h.

66. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
Regard 𝑠d and 𝑎d as observed values.
Regard 𝑆df), ⋯ , 𝑆h and 𝐴df), ⋯ , 𝐴h as random variables.

67. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
Regard 𝑆df), ⋯ , 𝑆h and 𝐴df), ⋯ , 𝐴h as random variables.

68. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
• 𝑆df) ~ 𝑝 ⋅ 𝑠d, 𝑎d ,
⋮
• 𝑆h ~ 𝑝 ⋅ 𝑠h7), 𝑎h7) .
• 𝐴df) ~ 𝜋 ⋅ 𝑠df) ,
⋮
• 𝐴h ~ 𝜋 ⋅ 𝑠h .

69. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.

70. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.

71. Action-Value Function 𝑄. 𝑠, 𝑎
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
• 𝑄. 𝑠d, 𝑎d depends on 𝑠d, 𝑎d, 𝜋, and 𝑝.
• 𝑄. 𝑠d, 𝑎d is dependent of 𝑆df), ⋯ , 𝑆h and 𝐴df), ⋯ , 𝐴h.

72. State-Value Function 𝑉
. 𝑠
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
Definition: State-value function.
• 𝑉
. 𝑠d = 𝔼s 𝑄. 𝑠d, 𝐴 = ∑ 𝜋 𝑎 𝑠d ⋅ 𝑄. 𝑠d, 𝑎
t . (Actions are discrete.)
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .

73. State-Value Function 𝑉
. 𝑠
Definition: State-value function.
• 𝑉
. 𝑠d = 𝔼s 𝑄. 𝑠d, 𝐴
Taken w.r.t. the action 𝐴 ∼ 𝜋 ⋅ 𝑠d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .

74. State-Value Function 𝑉
. 𝑠
Definition: State-value function.
• 𝑉
. 𝑠d = 𝔼s 𝑄. 𝑠d, 𝐴 = ∑ 𝜋 𝑎 𝑠d ⋅ 𝑄. 𝑠d, 𝑎
t . (Actions are discrete.)
Taken w.r.t. the action 𝐴 ∼ 𝜋 ⋅ 𝑠d .
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .

75. State-Value Function 𝑉
. 𝑠
Definition: State-value function.
• 𝑉
. 𝑠d = 𝔼s 𝑄. 𝑠d, 𝐴 = ∑ 𝜋 𝑎 𝑠d ⋅ 𝑄. 𝑠d, 𝑎
t . (Actions are discrete.)
• 𝑉
. 𝑠d = 𝔼s 𝑄. 𝑠d, 𝐴 = ∫ 𝜋 𝑎 𝑠d ⋅ 𝑄. 𝑠d, 𝑎 𝑑𝑎 . (Actions are continuous.)
• 𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾*
𝑅df* + ⋯ + 𝛾h7d
𝑅h.
Definition: Discounted return.
Definition: Action-value function.
• 𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d | 𝑆d = 𝑠d, 𝐴d = 𝑎d .

76. Understanding the Value Functions
• Action-value function: 𝑄. 𝑠, 𝑎 = 𝔼 𝑈d|𝑆d = 𝑠, 𝐴d = 𝑎 .
• Given policy 𝜋, 𝑄. 𝑠, 𝑎 evaluates how good it is for an agent to pick
action 𝑎 while being in state 𝑠.

77. • Action-value function: 𝑄. 𝑠, 𝑎 = 𝔼 𝑈d|𝑆d = 𝑠, 𝐴d = 𝑎 .
• Given policy 𝜋, 𝑄. 𝑠, 𝑎 evaluates how good it is for an agent to pick
action 𝑎 while being in state 𝑠.
• State-value function: 𝑉
. 𝑠 = 𝔼s 𝑄. 𝑠, 𝐴
• For fixed policy 𝜋, 𝑉
. 𝑠 evaluates how good the situation is in state 𝑠.
• 𝔼u 𝑉
. 𝑆 evaluates how good the policy 𝜋 is.
Understanding the Value Functions

78. Evaluating Reinforcement Learning

79. • Gym is a toolkit for developing and comparing reinforcement learning algorithms.
• https://gym.openai.com/
OpenAI Gym

80. • Gym is a toolkit for developing and comparing reinforcement learning algorithms.
• https://gym.openai.com/
OpenAI Gym
Cart Pole Pendulum
Classical control problems

81. • Gym is a toolkit for developing and comparing reinforcement learning algorithms.
• https://gym.openai.com/
OpenAI Gym
Pong Space Invader
Atari Games
Breakout

82. • Gym is a toolkit for developing and comparing reinforcement learning algorithms.
• https://gym.openai.com/
OpenAI Gym
Ant Humanoid
MuJoCo (Continuous control tasks.)
Half Cheetah

83. OpenAI Gym

84. Play CartPole Game
• Get the environment of CartPole from Gym.
• “env” provides states and reward.

85. Play CartPole Game
A random action.
“done=1” means finished (win or lose the game)
A window pops up rendering CartPole.

86. Summary

87. • Agent
• Environment
• State 𝑠
• Action 𝑎
• Reward 𝑟
Summary
Terminologies

88. • Agent
• Environment
• State 𝑠
• Action 𝑎
• Reward 𝑟
• Policy 𝜋 𝑎 𝑠
• State transition 𝑝 𝑠_
𝑠, 𝑎
Summary
Terminologies

89. • Agent
• Environment
• State 𝑠
• Action 𝑎
• Reward 𝑟
• Policy 𝜋 𝑎 𝑠
• State transition 𝑝 𝑠_
𝑠, 𝑎
Summary
Terminologies Return and Value
• Return:
𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾* 𝑅df* + ⋯

90. • Agent
• Environment
• State 𝑠
• Action 𝑎
• Reward 𝑟
• Policy 𝜋 𝑎 𝑠
• State transition 𝑝 𝑠_
𝑠, 𝑎
Summary
Terminologies Return and Value
• Return:
𝑈d = 𝑅d + 𝛾 𝑅df) + 𝛾* 𝑅df* + ⋯
• Action-value function:
𝑄. 𝑠d, 𝑎d = 𝔼 𝑈d|𝑠d, 𝑎d .
• State-value function:
𝑉
. 𝑠d = 𝔼s~. 𝑄. 𝑠d, 𝐴 .

91. Play game using AI
𝑠d7) 𝑎d7) 𝑠d
𝑟d7* 𝑟d7)
⋯
Time t

92. Play game using AI
𝑠d7) 𝑎d7) 𝑠d
𝑟d7* 𝑟d7)
⋯ 𝑎d
𝜋
Time t

93. Play game using AI
𝑠d7) 𝑎d7) 𝑠d
𝑟d7* 𝑟d7)
⋯ 𝑎d 𝑠df)
𝑟d
𝑝
Time t

94. Play game using AI
𝑠d7) 𝑎d7) 𝑠d
𝑟d7* 𝑟d7)
⋯ 𝑎d 𝑠df)
𝑟d
Time t Time t+1
⋯

95. Thank You!
http://wangshusen.github.io/