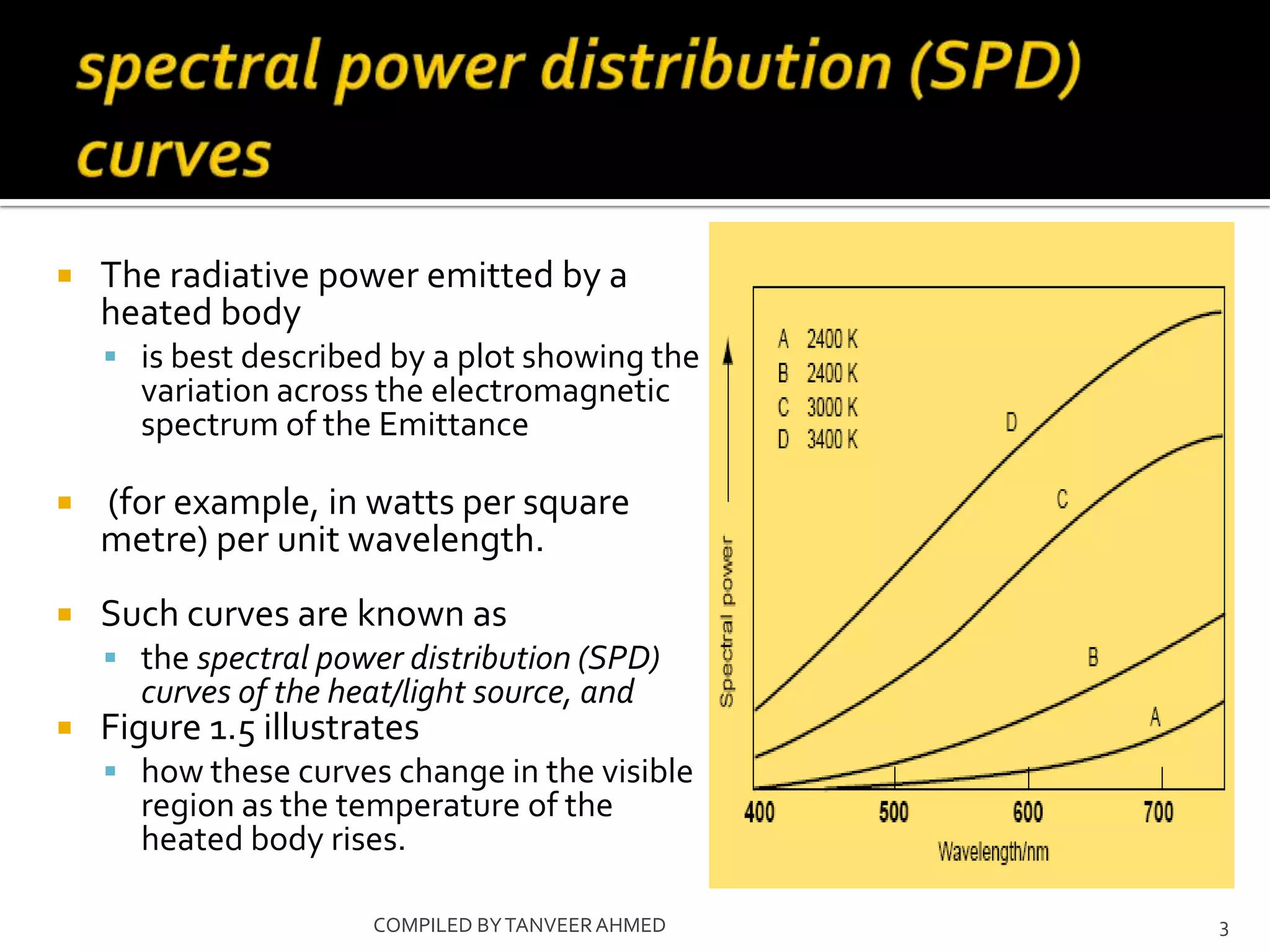
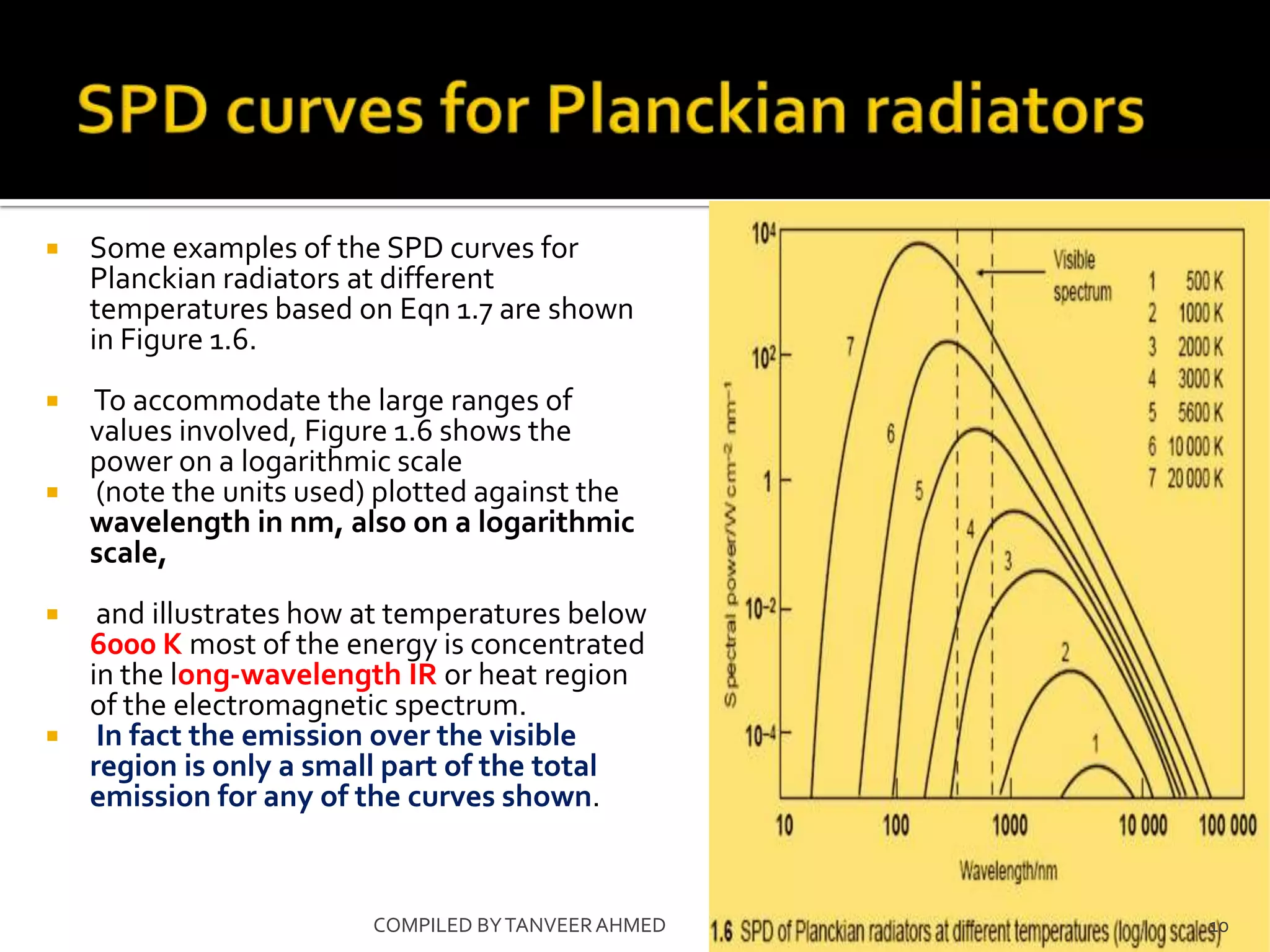
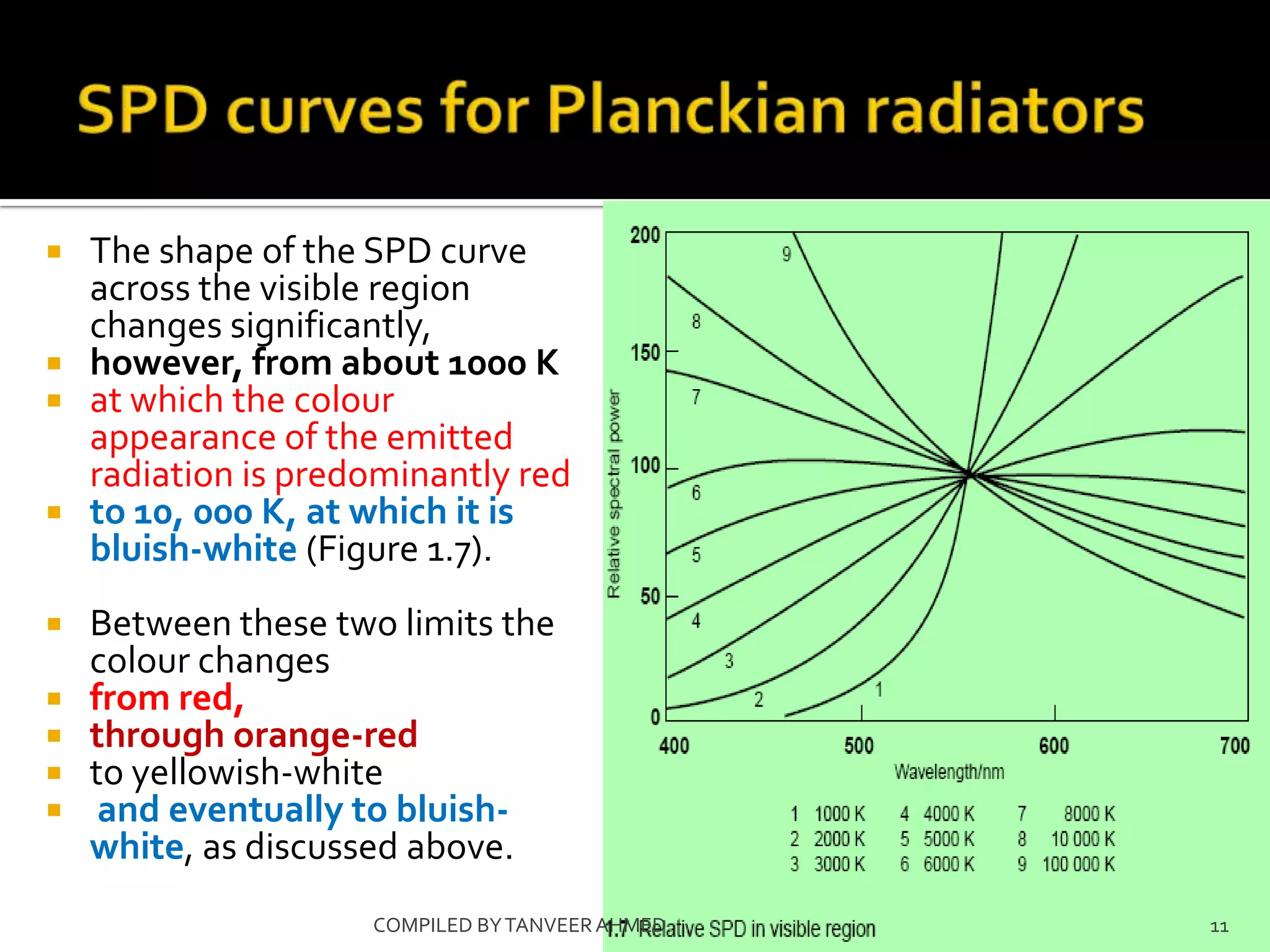
The document discusses spectral power distribution (SPD) curves, which describe the variation of emittance across the electromagnetic spectrum for different temperature heat sources. SPD curves change as temperature increases, shifting from red to orange to yellow and eventually white-hot. Max Planck developed a theoretical treatment in 1900 that correctly predicted the form of SPD curves for different temperatures, known as Planckian radiation. The curves show how radiation is concentrated in the infrared at lower temperatures below 6000K and shifts across the visible spectrum from red to blue-white as temperature increases from 1000K to 10,000K.

1. spectral power distribution (SPD) curves of the heat/light source,
COMPILED BY TANVEER AHMED 1

2.  When a coal fire is lit
 (or when the bar of an electric fire is switched
on), it first of all
▪ glows a dull red,
▪ then orange-red,
▪ then yellow;
 eventually it approaches the ‘white-hot’ stage
as the temperature rises.
 At the same time the total amount of energy
emitted rises (the fire gets steadily hotter).
COMPILED BY TANVEER AHMED 2

3.  The radiative power emitted by a
heated body
 is best described by a plot showing the
variation across the electromagnetic
spectrum of the Emittance
 (for example, in watts per square
metre) per unit wavelength.
 Such curves are known as
 the spectral power distribution (SPD)
curves of the heat/light source, and
 Figure 1.5 illustrates
 how these curves change in the visible
region as the temperature of the
heated body rises.
COMPILED BY TANVEER AHMED 3

4.  A Planckian or black body radiator is an
idealised radiation source consisting of a
▪ heated enclosure from which radiation escapes through
an opening whose area is small
▪ compared to the total internal surface area of the
enclosure
 (in practice approximated to by a small hole
in the side of a large furnace).
COMPILED BY TANVEER AHMED 4

5.  The term ‘black body’ was originally used in
recognition that
▪ such a model source would radiate energy perfectly
▪ and conversely would absorb light perfectly,
▪ without reflecting any of it away,
▪ in the manner of an ideal black object.
 Nowadays such a model source is referred to
as an ideal, full or Planckian radiator.
COMPILED BY TANVEER AHMED 5

6.  The Austrian physicist Josef Stefan showed
in 1879 that
 the total radiation emitted
 by such a heated body
 depended only on its temperature
 and was independent of
▪ the nature of the material from which it was
constructed.
COMPILED BY TANVEER AHMED 6

7.  Considerable debate about the spectral
distribution from these
▪ so-called black bodies ensued,
 in which many of the world’s leading
theoretical and practical physicists joined:
these included
▪ Wien,
▪ Jeans
▪ and Lord Rayleigh.
COMPILED BY TANVEER AHMED 7

8.  In 1900, however, the German physicist Max Planck
developed a theoretical treatment that
▪ correctly predicted the form of the spectral power distribution curves
▪ for different temperatures
 (it took the support of Einstein in 1905 to convince the
sceptics).
 Planck’s breakthrough came through the assumption
 that
▪ radiation was not emitted continuously
▪ but only in small packets or quanta,
▪ With the energy of the quantum being directly proportional to the
frequency of the radiation involved
COMPILED BY TANVEER AHMED 8

9.  Planck used his now famous Eqn 1.5 to
derive an expression for
▪ the spectral emittance
▪ from which the SPD curve of the source can be calculated.
 The Planckian radiation expression has the
form of Eqn 1.7:
COMPILED BY TANVEER AHMED 9

10.  Some examples of the SPD curves for
Planckian radiators at different
temperatures based on Eqn 1.7 are shown
in Figure 1.6.
 To accommodate the large ranges of
values involved, Figure 1.6 shows the
power on a logarithmic scale
 (note the units used) plotted against the
wavelength in nm, also on a logarithmic
scale,
 and illustrates how at temperatures below
6000 K most of the energy is concentrated
in the long-wavelength IR or heat region
of the electromagnetic spectrum.
 In fact the emission over the visible
region is only a small part of the total
emission for any of the curves shown.
COMPILED BY TANVEER AHMED 10

11.  The shape of the SPD curve
across the visible region
changes significantly,
 however, from about 1000 K
 at which the colour
appearance of the emitted
radiation is predominantly red
 to 10, 000 K, at which it is
bluish-white (Figure 1.7).
 Between these two limits the
colour changes
 from red,
 through orange-red
 to yellowish-white
 and eventually to bluish-
white, as discussed above.
COMPILED BY TANVEER AHMED 11

12.  The closest approach to the
 ideal equi-energy (ideal white light) source
with constant emittance
▪ across the visible spectrum
▪ occurs somewhere between 5000 and 6000 K.
 Thus we can associate the colour appearance
of the source with the temperature
▪ at which a Planckian radiator will give approximately the same
colour appearance.
COMPILED BY TANVEER AHMED 12

13.  The precise connection between
▪ colour temperature
▪ and Planckian radiator temperature
▪ (and that of correlated colour temperature)
 is best discussed through a plot of
▪ the colour coordinates of the Planckian radiators on a suitable CIE
chromaticity diagram
 The typical 100 W domestic tungsten light bulb has a
▪ colour temperature of about 2800 K.
 That of a tungsten–halogen projector bulb
▪ is about 3100 K,
 whilst that of average daylight from an overcast sky
▪ is about 6500 K.
COMPILED BY TANVEER AHMED 13