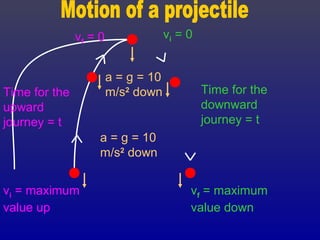
This document discusses vertical projectile motion and free fall. It explains that during vertical projectile motion, an object thrown upwards experiences maximum velocity on release, slows as it rises, stops at the top of its path, and then speeds up as it descends. The acceleration due to gravity causes the downward motion and is always 10 m/s^2. Equations of motion can be used to analyze the path of a vertically thrown object. When objects fall through air, air resistance reduces their acceleration until they reach terminal velocity, where acceleration equals zero and the object falls at a constant speed.

1. XOLANI ERIC MAKONDO
• VERTICAL PROJECTILE MOTION

2. Skydiver
diving off cliff

3. What happens during the motion of a
ball that is thrown upwards into the air?

4. Describe the motion -
• The object starts with maximum velocity
as it leaves the throwers hand
• The object slows down as it rises in the air
• The object momentarily stops at the top
• The object speeds up as it descends
• The final velocity of the object when it
again reaches the throwers hand is the
same as when it left the throwers hand
• At all times the object accelerates
downwards due to the force of gravity.

5. Time for the
downward
journey = t
Time for the
upward
journey = t
a = g = 10
m/s2
down
a = g = 10
m/s2
down
vf = 0
vi = maximum
value up
vf = maximum
value down
vi = 0

6. ACCELERATION
• At any point during the journey the
acceleration of the object is equal to the
gravitational acceleration, g.
• g = 10m/s2
down towards
the earth.
• g is independent of the
mass of the object.
• g is dependent upon
the distance from the
centre of the earth

7. Use equations of motion -
vf = vi + gt
Δx = vit + ½ gt2
vf
2
= vi
2
+ 2gs
Δx = (vf + vi) . t
2

8. t
s/m
GRAPHS of MOTION for PROJECTILE
MOTION
t
g/m/s2
t
s/m
t
v/m/s
Gradient of the
graph = - 10m/s2
a = g= -10m/s2
down
Disp./time
Velocity/time
Acceleration/time
Distance/time

9. FREE FALL and TERMINAL VELOCITY
• Objects only accelerate downwards at 10
m/s2
(or 9,8m/s2
) in a vacuum near earths
surface.
• In air, air resistance increases and decreases
acceleration to values less than 10 m/s2
.
• Smooth objects experience less air
resistance and a = g initially for all objects.
• If air resistance is large and increasing,
acceleration decreases to zero and the object
falls at constant velocity, called terminal
velocity

10. When the parachutist jumps,
her acceleration is
10 m/s2
downwards. The only force acting
on her is the
force of the earth.
Fres is downwards
As her velocity increases, so does
the force of air resistance opposing
the downward force of gravity.
Fres is still downwards, but smaller.

11. Air resistance is due to collisions with
the particles of air.
The greater the velocity of the parachutist, the
greater the number of collisions and the greater
the air resistance.
Fres decreases until it equals zero and a = 0.
The parachutist now
falls with a constant
velocity – called
terminal velocity

12. What are you expected to do?
• Apply equations of motion to vertical
motion.
• Use graphs of motion to describe vertical
motion.
• Explain why some objects reach terminal
velocity when falling in the gravitational
field.

13. Tips to help you use the equations
of motion for projectile motion:
• Choose a direction as positive.
• Decide on the time interval that is relevant
to the question.
• Write down known values - vi, vf, a, ∆x and
t.
• If an object is released or dropped by a
person that is moving up or down at a
certain velocity, the initial velocity of the
object equals the velocity of that person.

14. Apply your knowledge!!!
A bullet is fired vertically upwards at 200m/s.
Ignore the effects of air resistance, and
calculate:
a. the maximum height reached.
b. the time taken for the bullet to be at a
height of 1500m on its way down.
c. at what height it will be moving at 100m/s
upwards.

15. This is how your answer should look:
a. Let up be positive for all answers
vi = +200 m/s
vf = 0 m/s
g = -10 m/s2
∆x = ?
vf
2
= vi
2
+ 2g∆x
0 = (200)2
+ 2(-10) ∆x
∆x = + 2000m or 2000m up

16. b. Consider the time period from when the
bullet was fired until it is 500m above the
starting position.
vi = +200m/s g = -10m/s2
∆x = +500m t = ?
∆x = vit + ½ gt2
+500 = (+200)t + ½ (-10)t2
t = 10s or 30s
30s is when the bullet is on the way
down.

17. c. Consider the time interval from when the
bullet is fired until it has a velocity of
100m/s upwards
vi = +200m/s
vf = +100m/s
g = -10m/s2
vf
2
= vi
2
+ 2g ∆x
(+100)2
= (+200)2
+ 2(-10)s
s = 1500m

18. The acceleration due to gravity is 9.8 m.s-2
.
It can differ from point to point on the earths
surface – depending on the distance from
the centre of the earth. All objects fall at this
rate – irrespective of their mass.
However, we usually take it (g) as 10 m.s-2
.
Discuss how the acceleration due to
gravity could be determined by using a
ticker tape and ticker timer.

19. Position of
object
Time/s Displacement/m Velocity/m.s-1
Acc. Due to gravity/m.s-2
0 0 0 10
1 5 10 10
2 20 20 10
3 45 30 10
4 80 40 10
Fallingobject
Calculate the acceleration due to gravity from these values

20. How can the value of g be determined by using
the set up above and the equation
∆x = vit + 1
/2 g t2
?
Pendulu
m
method

21. Since the pendulum starts from rest, vi = 0 m.s-1
∆x = 1
/2 g t2
The pendulum falls about 84 cm. in the time
the metre rule falls through ¼ of a swing.
Take the time for 20 swings of the
pendulum and then divide by 80 to find the
time for ¼ of a swing.
Substitute into equation and solve for g.

22. In a vacuum all objects, irrespective of mass,
shape or size, fall at the same rate of
9.8m.s-2
In reality, ‘g’ varies from point to point on the
earth’s surface. This depends upon:
1. The change in radius from point to point.
2. The varying density of the earth’s surface
from point to point.
At the poles ‘g’ is greater and less at the
equator.