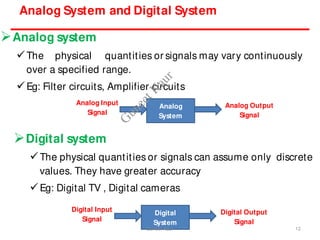
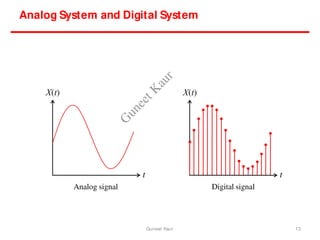
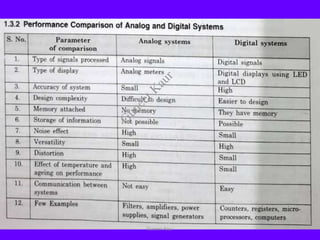
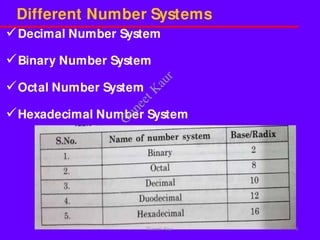
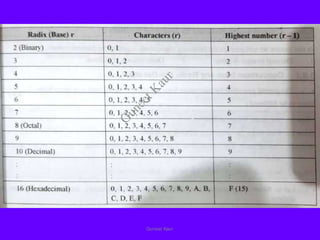
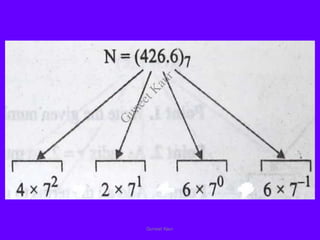
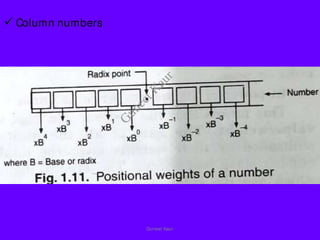
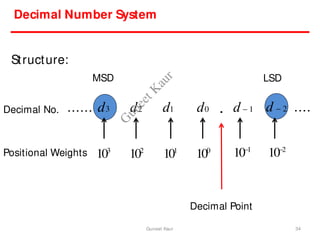
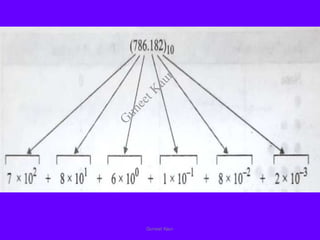
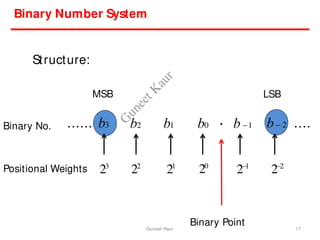
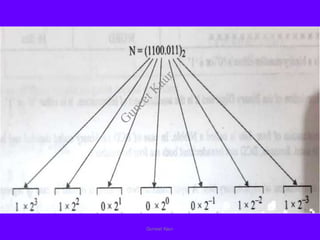
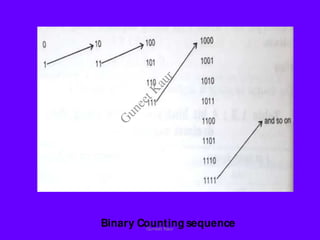
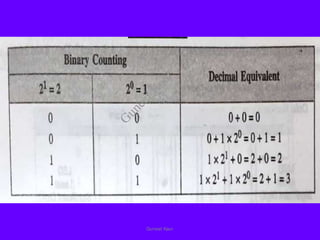
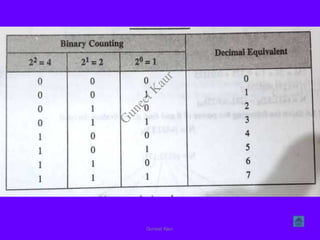
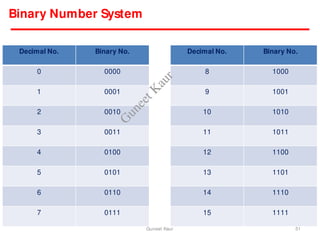
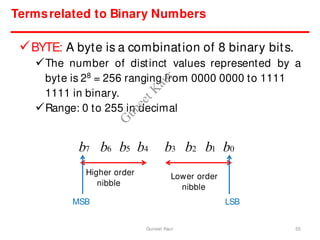
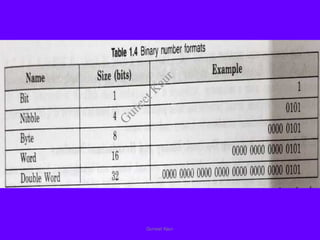
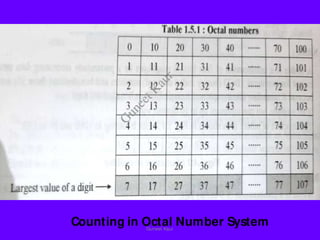
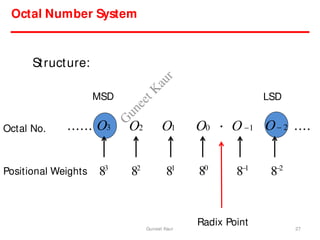
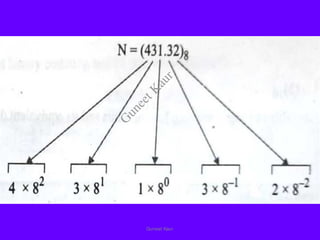
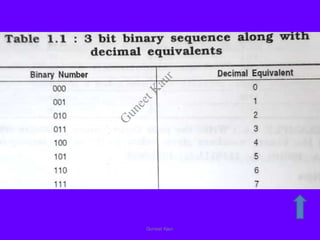
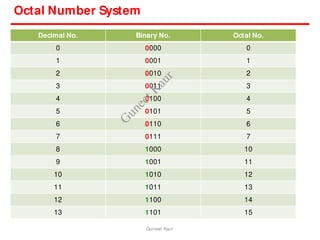
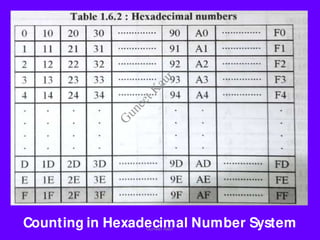
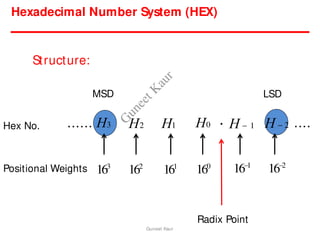
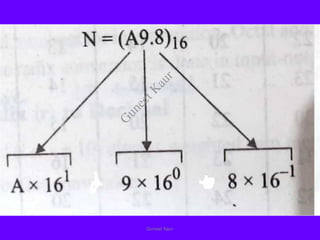
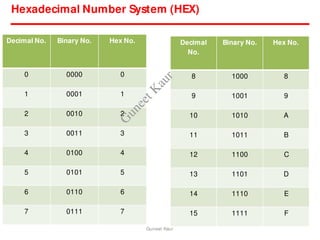
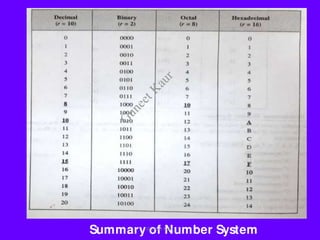
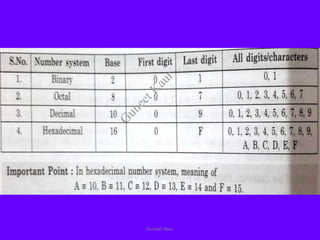
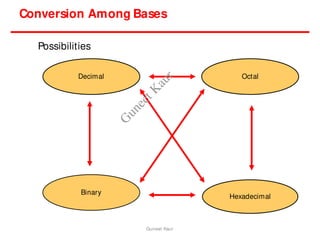
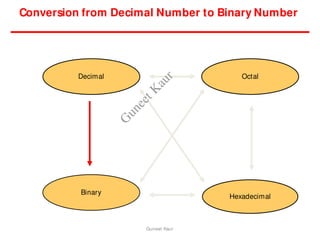
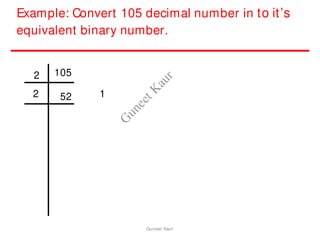
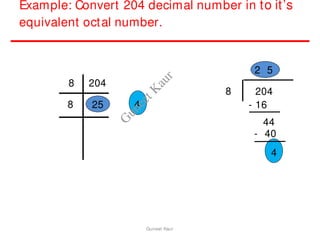
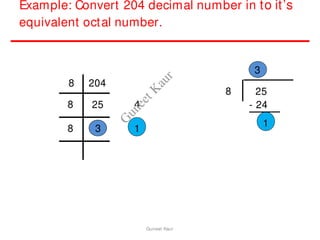
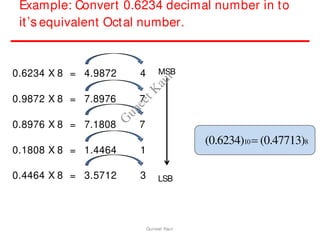
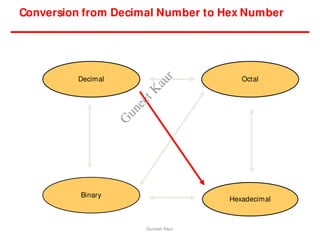
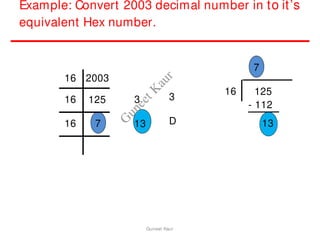
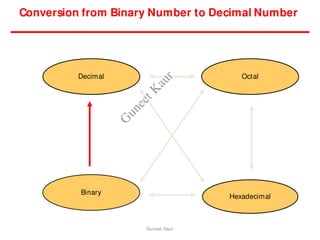
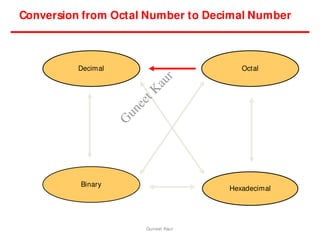
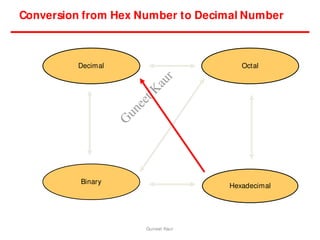
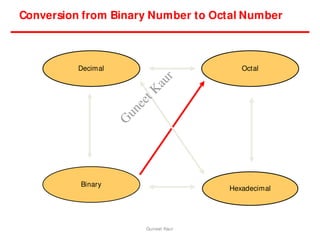
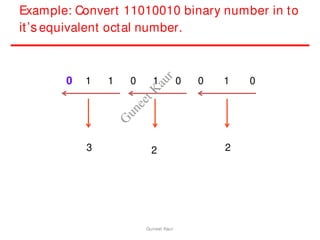
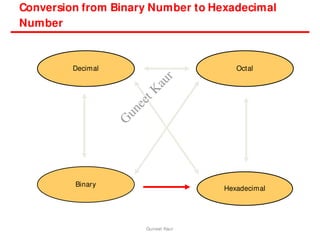
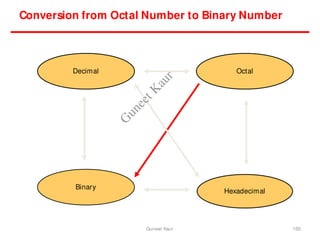
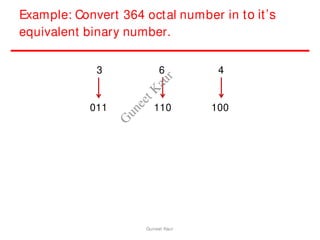
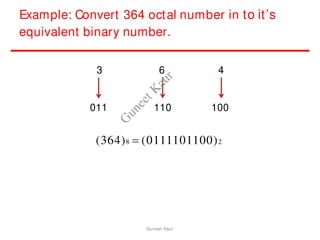
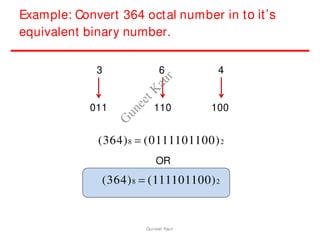
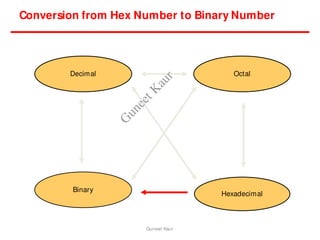
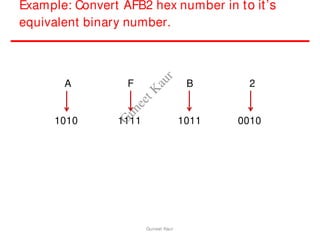
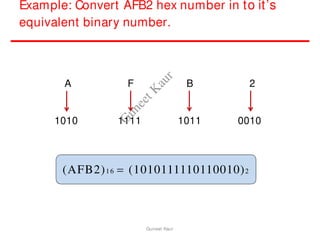
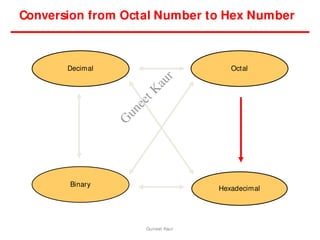
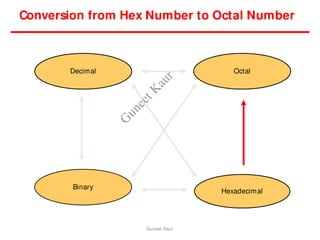
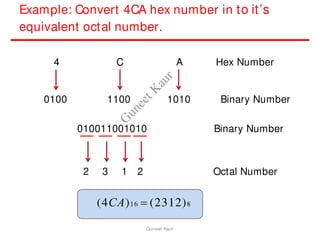
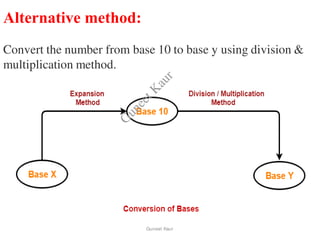
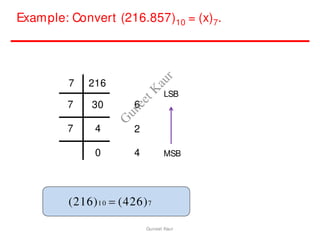
The document outlines a course on digital circuits and logic design, focusing on the understanding and implementation of basic digital circuits and the conversion of number systems. It covers various topics including analog and digital signals, different number systems (decimal, binary, octal, hexadecimal), their conversions, and comparative advantages of digital systems over analog systems. Key concepts include binary logic, signals, and system structures related to digital technology.

1. Digital Circuit and Logic Design
1
Guneet Kaur
Associate Professor,
Department of Electronics & Communication Engineering,
Amritsar Group of Colleges, Amritsar
Subject Code: ACEC - 16302
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

2. Objectives
The student will be able to:
Understand basic digital circuits.
Understand conversion of number systems.
Implement combinational and sequential circuits.
Understand logic families, data converters.
2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

3. M odule I - Number System and Binary Code
 Basic Concepts:
• Introduction to analog signal and digital signal
• Advantages of digital signals
• Comparison between analog signal and digital signal
• Introduction to analog system and digital system
• Drawbacks of analog systems
• Advantages of digital system over analog system
• Limitations of digital techniques
• Comparison between analog system and digital system
• Binary logic and Logic levels
 Study different number systems: Different types of number
systems (Decimal, Binary, Octal, Hexadecimal),
 Conversion of number systems: Make conversion from one
number system to another. 3
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

4. Basic Concepts
4
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

5. Analog Signal and Digital Signal
Signal:
A physical quantity, which contains some
information and which is a function of one or more
independent variables.
Type of Signals:
Signals
5
Analog Signals Digital Signals
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

6. Analog Signals:
 Analog signals are the signals which may have infinite number of
different magnitudes or values.
 They vary continuous with time.
Digital Signals:
 A digital signal is one which changes between two discrete levels
of voltage or values . These discrete levels are represented by
terms of Low and High or True and False or 1 and 0.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

7.  The digital signal has only a finite number of predetermined
distinct magnitudes.
 Actually, the digital signals are the discrete time signals.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

8. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

9. Advantages of digital signals:
•Various communication medium can use these signals
•
•Can be compressed
•Electronic circuitry cheap
•Multiplexing can be done
•More secure
•Several users can be connected
•Can make easy connections
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

10. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

11. Analog System and Digital System
System:
It is defined as the physical device or group of
devices or algorithm which performs the required
operations on the signal applied at its input.
Type of Systems:
Systems
11
Analog Systems Digital Systems
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

12. Analog System and Digital System
Analog system
The physical quantities or signals may vary continuously
over a specified range.
Eg: Filter circuits, Amplifier circuits
Digital system
The physical quantities or signals can assume only discrete
values. They have greater accuracy
Eg: Digital TV , Digital cameras
12
Analog
System
Analog Input
Signal
Analog Output
Signal
Digital
System
Digital Input
Signal
Digital Output
Signal
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

13. t
X(t)
Analog signal
t
X(t)
Digital signal
13
Analog System and Digital System
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

14. Drawbacks of analog systems:
•Less accurate
•Analysis is difficult
•Affected by disturbance or noise
•Component ageing and temperature variations
•Less reliable
•Less versatile
•Small accuracy
•Storage of information is not possible
•Cannot control computerized
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

15. Advantages of Digital System over Analog System
1. Accuracy & Precision are greater
2. Digital Systems are easier to design
3. Information storage is easy
4. Digital circuits are less affected by noise
5. Highly reliable and cost efficient
6. Less affected by ageing and temperature variations
7. More digital circuitry can be fabricated on ICchips
8. Easier to communicate
9. Faster response
10.Digital systems are more versatile
15
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

16. Limitations of Digital Techniques
16
The real world is basically ‘Analog’
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

17. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

18. Binary Logic and Logic levels
18
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

19. Logic levels:
.Positive Logic
. Negative Logic
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

20. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

21. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

22. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

23. Number Systems
23
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

24. Number System
A number system defines a set of values used to
represent quantity.
Set of rules and symbols used to represent numbers
24
Weighted or
Positional
Number Systems
Non - Weighted or
Non - Positional
Number Systems
Number Systems
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

25. Different Number Systems
Decimal Number System
Binary Number System
Octal Number System
Hexadecimal Number System
9
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

26. Few Common Aspects to all Numbering Systems
Base or Radix: Total number of different symbols
used in the number system
Eg: Since counting in decimal involves ten symbols,
we can say that its base or radix is ten.
The largest value of a digit is always one less than
radix (r) or base (b) i.e. (r – 1) or (b – 1).
26
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

27. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

28.  Each digit position (i.e., place) represents a different
multiple of base
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

29. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

30.  Column numbers
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

31. Decimal Number System
Decimal number system contains ten unique
symbols 0,1,2,3,4,5,6,7,8 and 9
Since counting in decimal involves ten symbols,
we can say that its base or radix is ten.
It is a positional weighted system
31
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

32. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

33. Decimal Number System
In this system, any number (integer, fraction or
mixed) of any magnitude can be represented
by the use of these ten symbols only
Each symbols in the number is called a “Digit”
33
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

34. Decimal Number System
Structure:
Positional Weights
d2 d1 d0 . d  1
103
102
101
100
101
102
Decimal No. ...... d3 d  2 ....
Decimal Point
MSD LSD
34
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

35. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

36. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

37. Decimal Number System
MSD: The leftmost digit in any number
representation, which has the greatest positional
weight out of all the digits present in that number
is called the “Most Significant Digit” (MSD)
LSD: The rightmost digit in any number
representation, which has the least positional
weight out of all the digits present in that number
is called the “Least Significant Digit” (LSD)
37
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

38. Decimal Number System
Examples
214.5
0.594
9875.54
38
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

39. 0 10 20 30 40 50 60 70 80 90 100 110
1 11 21 … … … … … … 101 …
2 12 22 … … … … … … 102 …
3 13 23 … … … … … … 103 …
4 14 24 … … … … … … 104 …
5 15 25 … … … … … … 105 …
6 16 26 … … … … … … 106 …
7 17 27 … … … … … … 107 …
8 18 28 … … … … … … 108 …
9 19 29 39 49 59 69 79 89 99 109 119
Counting in Decimal Number System
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

40. Binary Number System
Binary number system is a positional weighted
system
It contains two unique symbols 0 and 1
Since counting in binary involves two symbols,
we can say that its base or radix is two.
40
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

41. A binary digit is called a “Bit”
A binary number consists of a sequence of
bits, each of which is either a 0 or a 1.
The binary point separates the integer and
fraction parts
Binary Number System
41
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

42. 17
Binary Number System
Structure:
Binary No.
Positional Weights
b2 b1 b0 . b 1
23
22
21
20
21
22
...... b3 b 2 ....
Binary Point
MSB LSB
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

43. MSB: The leftmost bit in a given binary
number with the highest positional weight is
called the “Most Significant Bit” (MSB)
LSB: The rightmost bit in a given binary
number with the lowest positional weight is
called the “Least Significant Bit” (LSB)
Binary Number System
43
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

44. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

45. Binary Counting sequence
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

46. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

47. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

48. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

49. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

50. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

51. Binary Number System
51
Decimal No. Binary No.
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
Decimal No. Binary No.
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

52. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

53. BIT: The binary digits (0 and 1) are called bits.
- Single unit in binary digit is called “Bit”
- Example 1
0
Termsrelated to Binary Numbers
53
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

54. NIBBLE: A nibble is a combination of 4 binary
bits.
1110
0000
1001
0101
Termsrelated to Binary Numbers
54
The number of distinct values represented by a
nibble is 24
= 16 ranging from 0000 to 1111 in binary.
Range : 0 to 15 in decimal
Examples:
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

55. BYTE: A byte is a combination of 8 binary bits.
The number of distinct values represented by a
byte is 28
= 256 ranging from 0000 0000 to 1111
1111 in binary.
Range: 0 to 255 in decimal
Termsrelated to Binary Numbers
LSB
b7 b6 b5
Higher order
nibble
MSB
b4 b3 b2 b1 b0
Lower order
nibble
55
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

56.  WORD: A word is a combination of 16 binary bits. Hence it consists of
two bytes.
b2 b1 b0
MSB LSB
b15 b14 b13 b12b11 b10
Higher order byte
56
b9 b8 b7 b6 b5 b4 b3
Lower order byte
 The number of distinct values represented by a word
is 216
= 65536 ranging from 0000 0000 0000 0000 to 1111 1111
1111 1111 in binary.
 Range: 0 to 65535 in decimal
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

57. DOUBLE WORD: A double word is exactly what
its name implies, two words
-It is a combination of 32 binary bits.
Termsrelated to Binary Numbers
57
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

58. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

59. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

60. Octal Number System
Octal number system is a positional weighted
system
It contains eight unique symbols 0,1,2,3,4,5,6
and 7
Since counting in octal involves eight symbols,
we can say that its base or radix is eight.
60
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

61. The largest value of a digit in the octal system
will be 7.
That means the octal number higher than 7
will not be 8, instead of that it will be 10.
Octal Number System
61
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

62. Counting in Octal Number System
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

63. 27
Octal Number System
Structure:
Octal No.
Positional Weights
O2 O1 O0 . O 1
80
83
82
81
81
82
...... O3 O 2 ....
Radix Point
MSD LSD
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

64. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

65. 40
Octal Number System
Since its base 8  23
,every 3 bit group of binary
can be represented by an octal digit.
An octal number is thus 1/ 3rd the length of the
corresponding binary number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

66. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

67. Octal Number System
Decimal No. Binary No. Octal No.
0 0000 0
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 0110 6
7 0111 7
8 1000 10
9 1001 11
10 1010 12
11 1011 13
12 1100 14
13 1101 15
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

68. Hexadecimal Number System (HEX)
Binary numbers are long. These numbers are
fine for machines but are too lengthy to be
handled by human beings. So there is a need to
represent the binary numbers concisely.
One number system developed with this
objective is the hexadecimal number system (or
Hex)
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

69. Hexadecimal Number System (HEX)
Hex number system is a positional weighted
system
It contains sixteen unique symbols
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E and F
.
Since counting in hex involves sixteen symbols,
we can say that its base or radix is sixteen.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

70. Counting in Hexadecimal Number System
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

71. Hexadecimal Number System (HEX)
Structure:
Hex No.
Positional Weights
H2 H1 H0 . H  1
160
163
162
161 161
162
...... H3 H  2 ....
Radix Point
MSD LSD
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

72. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

73. Hexadecimal Number System (HEX)
Since its base16  2,4
every 4 bit group of
binary can be represented by an hex digit.
An hex number is thus 1/ 4th the length of the
corresponding binary number
The hex system is particularly useful for
human communications with computer
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

74. Hexadecimal Number System (HEX)
Decimal No. Binary No. Hex No.
0 0000 0
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 0110 6
7 0111 7
Decimal
No.
Binary No. Hex No.
8 1000 8
9 1001 9
10 1010 A
11 1011 B
12 1100 C
13 1101 D
14 1110 E
15 1111 F
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

75. Summary of Number System
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

76. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

77. Guneet Kaur
G
u
n
e
e
t
K
a
u
r

78. Conversion of
Number Systems
78
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

79. Conversion Among Bases
Hexadecimal
Decimal Octal
Binary
Possibilities
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

80. Conversion from Decimal Number to Binary Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

81. Conversion of Decimal number into Binary number
(Integer Number)
Procedure:
1. Divide the decimal no by the base 2, noting the
remainder.
2. Continue to divide the quotient by 2 until there is
nothing left, keeping the track of the remainders
from each step.
3. List the remainder values in reverse order to find
the number’s binary equivalent
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

82. Example: Convert 105 decimal number in to it’s
equivalent binary number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

83. Example: Convert 105 decimal number in to it’s
equivalent binary number.
105
2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

84. Example: Convert 105 decimal number in to it’s
equivalent binary number.
2 105
2 52 1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

85. Example: Convert 105 decimal number in to it’s
equivalent binary number.
2 105
2 52
2 26
1
0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

86. Example: Convert 105 decimal number in to it’s
equivalent binary number.
2 105
2 52
2 26
2 13
1
0
0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

87. Example: Convert 105 decimal number in to it’s
equivalent binary number.
2 105
2 52
2 26
2 13
2 6
1
0
0
1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

88. Example: Convert 105 decimal number in to it’s
equivalent binary number.
2 105
2 52
2 26
2 13
2 6
2 3
1
0
0
1
0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

89. Example: Convert 105 decimal number in to it’s
equivalent binary number.
2 105
2 52
2 26
2 13
2 6
2 3
2 1
1
0
0
1
0
1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

90. Example: Convert (105 .42)10 decimal number
in to it’s equivalent binary number.
2 105
2 52
2 26
2 13
2 6
2 3
2 1
0
1
0
0
1
0
1
1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

91. Example: Convert (105 .42)10 decimal number
in to it’s equivalent binary number.
2 105
2 52
2 26
2 13
2 6
2 3
2 1
0
1
0
0
1
0
1
1
LSB
MSB
(105)10  (1101001)2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

92. Procedure:
1. Multiply the given fractional number by base 2.
2. Record the carry generated in this multiplication as
MSB.
3. Multiply only the fractional number of the product in
step 2 by 2 and record the carry as the next bit to MSB.
4. Repeat the steps 2 and 3 up to 5 bits. The last carry will
represent the LSB of equivalent binary number
Conversion of Decimal number into Binary number
(Fractional Number)
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

93. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

94. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
0.42 X 2 = 0.84 0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

95. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
0.42 X 2 = 0.84 0
0.84 X 2 = 1.68 1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

96. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
0.42 X 2 = 0.84 0
0.84 X 2 = 1.68 1
0.68 X 2 = 1.36 1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

97. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
0.42 X 2 = 0.84 0
0.84 X 2 = 1.68 1
0.68 X 2 = 1.36 1
0.36 X 2 = 0.72 0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

98. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
0.42 X 2 = 0.84 0
0.84 X 2 = 1.68 1
0.68 X 2 = 1.36 1
0.36 X 2 = 0.72 0
0.72 X 2 = 1.44 1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

99. Example: Convert 0.42 decimal number in to it’s
equivalent binary number.
0.42 X 2 = 0.84 0
0.84 X 2 = 1.68 1
0.68 X 2 = 1.36 1
0.36 X 2 = 0.72 0
0.72 X 2 = 1.44 1
MSB
(0.42)10  (0.01101)2
LSB
(15.42)10 = (1101001.01101)2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

100. Conversion from Decimal Number to Octal Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

101. Conversion of Decimal Number into Octal Number
(Integer Number)
Procedure:
1. Divide the decimal no by the base 8, noting the
remainder.
2. Continue to divide the quotient by 8 until there is
nothing left, keeping the track of the remainders
from each step.
3. List the remainder values in reverse order to find
the number’s octal equivalent
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

102. Example: Convert 204 decimal number in to it’s
equivalent octal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

103. Example: Convert 204 decimal number in to it’s
equivalent octal number.
8 204
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

104. Example: Convert 204 decimal number in to it’s
equivalent octal number.
8 204
8 25 4
8
2 5
204
- 16
44
- 40
4
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

105. Example: Convert 204 decimal number in to it’s
equivalent octal number.
8 204
8 25
8 3
4
1
8
3
25
- 24
1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

106. Example: Convert 204 decimal number in to it’s
equivalent octal number.
8 204
8 25
8 3
0
4
1
3
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

107. Example: Convert 204 decimal number in to it’s
equivalent octal number.
3
LSB
4
1
MSB
8 204
8 25
8 3
0
(204)10  (314)8
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

108. Procedure:
1. Multiply the given fractional number by base 8.
2. Record the carry generated in this multiplication as
MSB.
3. Multiply only the fractional number of the product in
step 2 by 8 and record the carry as the next bit to MSB.
4. Repeat the steps 2 and 3 up to 5 bits. The last carry will
represent the LSB of equivalent octal number
Conversion of Decimal Number into Octal Number
(Fractional Number)
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

109. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

110. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
0.6234 X 8 = 4.9872 4
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

111. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
0.6234 X 8 = 4.9872 4
0.9872 X 8 = 7.8976 7
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

112. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
0.6234 X 8 = 4.9872 4
0.9872 X 8 = 7.8976 7
0.8976 X 8 = 7.1808 7
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

113. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
0.6234 X 8 = 4.9872 4
0.9872 X 8 = 7.8976 7
0.8976 X 8 = 7.1808 7
0.1808 X 8 = 1.4464 1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

114. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
0.6234 X 8 = 4.9872 4
0.9872 X 8 = 7.8976 7
0.8976 X 8 = 7.1808 7
0.1808 X 8 = 1.4464 1
0.4464 X 8 = 3.5712 3
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

115. Example: Convert 0.6234 decimal number in to
it’s equivalent Octal number.
0.6234 X 8 = 4.9872 4
0.9872 X 8 = 7.8976 7
0.8976 X 8 = 7.1808 7
0.1808 X 8 = 1.4464 1
0.4464 X 8 = 3.5712 3
MSB
(0.6234)10 (0.47713)8
LSB
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

116. Conversion from Decimal Number to Hex Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

117. Conversion of Decimal Number into Hexadecimal
Number (Integer Number)
Procedure:
1. Divide the decimal no by the base 16, noting the
remainder.
2. Continue to divide the quotient by 16 until there is
nothing left, keeping the track of the remainders
from each step.
3. List the remainder values in reverse order to find
the number’s hex equivalent
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

118. Example: Convert 2003 decimal number in to it’s
equivalent Hex number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

119. Example: Convert 2003 decimal number in to it’s
equivalent Hex number.
16 2003
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

120. Example: Convert 2003 decimal number in to it’s
equivalent Hex number.
16 2003
16 125 3 3
1 2 5
16 2003
- 16
40
- 32
83
- 80
3
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

121. Example: Convert 2003 decimal number in to it’s
equivalent Hex number.
16 2003
16 125
16 7
3
13
3
D
7
16 125
- 112
13
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

122. Example: Convert 2003 decimal number in to it’s
equivalent Hex number.
16 2003
16 125
16 7
0
3
7
13
3
7
D
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

123. Example: Convert 2003 decimal number in to it’s
equivalent Hex number.
3
7
13
LSB
MSB
16 2003
16 125
16 7
0
(2003)10  (7 D3)16
3
7
D
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

124. Conversion of Decimal Number into Hexadecimal
Number (Fractional Number)
Procedure:
1. Multiply the given fractional number by base 16.
2. Record the carry generated in this multiplication as
MSB.
3. Multiply only the fractional number of the product in
step 2 by 16 and record the carry as the next bit to MSB.
4. Repeat the steps 2 and 3 up to 5 bits. The last carry will
represent the LSB of equivalent hex number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

125. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

126. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
0.122 X 16 = 1.952 1 1
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

127. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
0.122 X 16 = 1.952 1 1
0.952 X 16 = 15.232 15 F
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

128. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
0.122 X 16 = 1.952 1 1
0.952 X 16 = 15.232 15 F
0.232 X 16 = 3.712 3 3
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

129. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
0.122 X 16 = 1.952 1 1
0.952 X 16 = 15.232 15 F
0.232 X 16 = 3.712 3 3
0.712 X 16 = 11.392 11 B
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

130. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
0.122 X 16 = 1.952 1 1
0.952 X 16 = 15.232 15 F
0.232 X 16 = 3.712 3 3
0.712 X 16 = 11.392 11 B
0.392 X 16 = 6.272 6 6
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

131. Example: Convert 0.122 decimal number in to
it’s equivalent Hex number.
0.122 X 16 = 1.952 1 1
0.952 X 16 = 15.232 15 F
0.232 X 16 = 3.712 3 3
0.712 X 16 = 11.392 11 B
0.392 X 16 = 6.272 6 6
MSB
LSB
(0.122)10  (0.1F3B6)1 6
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

132. Conversion from Binary Number to Decimal Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

133. Procedure:
1. Write down the binary number.
2. Write down the weights for different positions.
3. Multiply each bit in the binary number with the
corresponding weight to obtain product numbers
to get the decimal numbers.
4. Add all the product numbers to get the decimal
equivalent
Conversion of Binary Number into Decimal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

134. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

135. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Binary No. 0 0
1 1 1 1
.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

136. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Binary No.
Positional Weights
0 0
1 1 1 1
.
23
22
21
20
21
22
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

137. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Binary No.
Positional Weights
0 0
1 1 1 1
.
23
22
21
20
21
22
(123
)(022
)(121
)(120
).(021
)(122
)
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

138. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Binary No.
Positional Weights
0 0
1 1 1 1
.
23
22
21
20
21
22
(123
)(022
)(121
)(120
).(021
)(122
)
= 8 + 0 + 2 + 1 . 0 + 0.25
110
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

139. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Binary No.
Positional Weights
0 0
1 1 1 1
.
23
22
21
20
21
22
(123
)(022
)(121
)(120
).(021
)(122
)
= 8 + 0 + 2 + 1 . 0 + 0.25
= 11.25
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

140. Example: Convert 1011.01 binary number in to
it’s equivalent decimal number.
Binary No.
Positional Weights
0 0
1 1 1 1
.
23
22
21
20
21
22
(123
)(022
)(121
)(120
).(021
)(122
)
= 8 + 0 + 2 + 1 . 0 + 0.25
= 11.25
( 1 0 1 1 . 0 1 ) 2  ( 1 1 . 2 5 ) 1 0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

141. Conversion from Octal Number to Decimal Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

142. Procedure:
1. Write down the octal number.
2. Write down the weights for different positions.
3. Multiply each bit in the binary number with the
corresponding weight to obtain product numbers
to get the decimal numbers.
4. Add all the product numbers to get the decimal
equivalent
Conversion of Octal Number into Decimal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

143. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

144. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Octal No. 2 4
3 6 5 .
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

145. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Octal No.
Positional Weights
3 6 5 .
82
81
80
2 4
81
82
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

146. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Octal No.
Positional Weights
2 4
3 6 5 .
82
81
80
81
82
(382
)(681
)(580
).(281
)(482
)
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

147. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Octal No.
Positional Weights
2 4
3 6 5 .
82
81
80
81
82
(382
)(681
)(580
).(281
)(482
)
= 192 + 48 + 5 . 0.25 + 0.0625
120
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

148. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Octal No.
Positional Weights
2 4
3 6 5 .
82
81
80
81
82
(382
)(681
)(580
).(281
)(482
)
= 192 + 48 + 5 . 0.25 + 0.0625
= 245.3125
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

149. Example: Convert 365.24 octal number in to it’s
equivalent decimal number.
Octal No.
Positional Weights
2 4
3 6 5 .
82
81
80
81
82
(382
)(681
)(580
).(281
)(482
)
= 192 + 48 + 5 . 0.25 + 0.0625
= 245.3125
(365.24)8  (245.3125)10
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

150. Conversion from Hex Number to Decimal Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

151. Procedure:
1. Write down the hex number.
2. Write down the weights for different positions.
3. Multiply each bit in the binary number with the
corresponding weight to obtain product numbers
to get the decimal numbers.
4. Add all the product numbers to get the decimal
equivalent
Conversion of Hexadecimal Number into Decimal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

152. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

153. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Hex No. 5 8 6
2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

154. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Hex No.
Positional Weights
5 8 6
2
163
162
161
160
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

155. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Hex No.
Positional Weights
5 8 6
2
163
162
161
160
(5163
)(8162
)(2161
)(6160
)
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

156. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Hex No.
Positional Weights
5 8 6
2
163
162
161
160
(5163
)(8162
)(2161
)(6160
)
= 20480 + 2048 + 32 + 6
130
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

157. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Hex No.
Positional Weights
5 8 6
2
163
162
161
160
(5163
)(8162
)(2161
)(6160
)
= 20480 + 2048 + 32 + 6
= 22566
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

158. Example: Convert 5826 hex number in to it’s
equivalent decimal number.
Hex No.
Positional Weights
5 8 6
2
163
162
161
160
(5163
)(8162
)(2161
)(6160
)
= 20480 + 2048 + 32 + 6
= 22566
(5826)16  (22566)10
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

159. Conversion from Binary Number to Octal Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

160. Procedure:
1. Group the binary bits into groups of 3 starting
from LSB.
2. Convert each group into its equivalent decimal.
As the number of bits in each group is
restricted to 3, the decimal number will be
same as octal number
Conversion of Binary Number into Octal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

161. Example: Convert 1101001 binary number in to
it’s equivalent octal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

162. Example: Convert 11010010 binary number in to
it’s equivalent octal number.
LSB
0 1 1 0 1 0 0 1 0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

163. Example: Convert 11010010 binary number in to
it’s equivalent octal number.
0 1 1 0 1 0 0 1 0
3 2 2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

164. Example: Convert 11010010 binary number in to
it’s equivalent octal number.
0 1 1 0 1 0 0 1 0
3 2 2
(11010010)2  (322)8
140
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

165. Conversion from Binary Number to Hexadecimal
Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

166. Procedure:
1. Group the binary bits into groups of 4 starting
from LSB.
2. Convert each group into its equivalent decimal.
As the number of bits in each group is
restricted to 4, the decimal number will be
same as hex number
Conversion of Binary Number to Hexadecimal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

167. Example: Convert 11010010 binary number in to
it’s equivalent hex number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

168. Example: Convert 11010010 binary number in to
it’s equivalent hex number.
LSB
1 1 0 1 0 0 1 0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

169. Example: Convert 11010010 binary number in to
it’s equivalent hex number.
LSB
1 1 0 1 0 0 1 0
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

170. Example: Convert 11010010 binary number in to
it’s equivalent hex number.
1 1 0 1 0 0 1 0
D 2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

171. Example: Convert 11010010 binary number in to
it’s equivalent hex number.
1 1 0 1 0 0 1 0
D
(11010010)2  (D 2)16
2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

172. Conversion from Octal Number to Binary Number
Hexadecimal
Decimal Octal
Binary
150
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

173. T
o get the binary equivalent of the given octal
number we have to convert each octal digit
into its equivalent 3 bit binary number
Conversion of Octal Number into Binary Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

174. Example: Convert 364 octal number in to it’s
equivalent binary number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

175. Example: Convert 364 octal number in to it’s
equivalent binary number.
3 6 4
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

176. Example: Convert 364 octal number in to it’s
equivalent binary number.
3 6 4
011 110 100
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

177. Example: Convert 364 octal number in to it’s
equivalent binary number.
3 6 4
011 110 100
(364)8  (0111101100)2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

178. Example: Convert 364 octal number in to it’s
equivalent binary number.
3 6 4
011 110 100
(364)8  (0111101100)2
OR
(364)8  (111101100)2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

179. Conversion from Hex Number to Binary Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

180. T
o get the binary equivalent of the given hex
number we have to convert each hex digit into
its equivalent 4 bit binary number
Conversion of Hexadecimal Number into Binary Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

181. Example: Convert AFB2 hex number in to it’s
equivalent binary number.
160
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

182. Example: Convert AFB2 hex number in to it’s
equivalent binary number.
A F B 2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

183. Example: Convert AFB2 hex number in to it’s
equivalent binary number.
A F B 2
1010 1111 1011 0010
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

184. Example: Convert AFB2 hex number in to it’s
equivalent binary number.
A F B 2
1010 1111 1011 0010
(AFB2)16  (1010111110110010)2
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

185. Conversion from Octal Number to Hex Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

186. T
o get hex equivalent number of given octal
number, first we have to convert octal number
into its 3 bit binary equivalent and then
convert binary number into its hex equivalent.
Conversion of Octal Number into Hexadecimal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

187. Example: Convert 364 octal number in to it’s
equivalent hex number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

188. Example: Convert 364 octal number in to it’s
equivalent hex number.
3 6 4 Octal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

189. Example: Convert 364 octal number in to it’s
equivalent hex number.
3 6 4 Octal Number
011 110 100 Binary Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

190. Example: Convert 364 octal number in to it’s
equivalent hex number.
3 6 4 Octal Number
011 110 100 Binary Number
011110100 Binary Number
170
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

191. Example: Convert 364 octal number in to it’s
equivalent hex number.
3 6 4 Octal Number
011 110 100 Binary Number
011110100 Binary Number
0 F 4 Hex Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

192. Example: Convert 364 octal number in to it’s
equivalent hex number.
(364)8  (F 4)16
3 6 4 Octal Number
011 110 100 Binary Number
011110100 Binary Number
0 F 4 Hex Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

193. Conversion from Hex Number to Octal Number
Hexadecimal
Decimal Octal
Binary
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

194. T
o get octal equivalent number of given hex
number, first we have to convert hex number
into its 4 bit binary equivalent
convert binarynumber into
and then
its octal
equivalent.
Conversion of Hexadecimal Number into Octal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

195. Example: Convert 4CA hex number in to it’s
equivalent octal number.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

196. Example: Convert 4CA hex number in to it’s
equivalent octal number.
4 C A Hex Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

197. Example: Convert 4CA hex number in to it’s
equivalent octal number.
4 C A Hex Number
0100 1100 1010 Binary Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

198. Example: Convert 4CA hex number in to it’s
equivalent octal number.
4 C A Hex Number
0100 1100 1010 Binary Number
010011001010 Binary Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

199. Example: Convert 4CA hex number in to it’s
equivalent octal number.
4 C A Hex Number
0100 1100 1010 Binary Number
010011001010 Binary Number
2 3 1 2 Octal Number
180
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

200. Example: Convert 4CA hex number in to it’s
equivalent octal number.
4 C A Hex Number
0100 1100 1010 Binary Number
010011001010 Binary Number
2 3 1 2
(4CA)16  (2312)8
Octal Number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

201. Alternative method:
Convert the number from base 10 to base y using division &
multiplication method.
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

202. Convert (1056)16 to ( ? )8
Solution-
Step-01: Conversion To Base 10-
(1056)16 → ( ? )10
Using Expansion method, we have-
(1056)16
= 1 x 163 + 0 x 162 + 5 x 161 + 6 x 160
= 4096 + 0 + 80 + 6
= (4182)10
From here, (1056)16 = (4182)10
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

203. Step-02: Conversion To Base 8-
(4182)10 → ( ? )8
Using Division method, we have-
From here, (4182)10 = (10126)8
Thus, (1056)16 = (10126)8
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

204. Convert (3211)4 to ( ? )5
Solution-
Step-01: Conversion To Base 10-
(3211)4 → ( ? )10
Using Expansion method, we have-
(3211)4
= 3 x 43 + 2 x 42 + 1 x 41 + 1 x 40
= 192 + 32 + 4 + 1
= (229)10
From here, (3211)4 = (229)10Guneet Kaur
G
u
n
e
e
t
K
a
u
r

205. Step-02: Conversion To Base 5-
(229)10 → ( ? )5
Using Division method, we have-
From here, (229)10 = (1404)5
Thus, (3211)4 = (1404)5
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

206. Conversion of a number with any radix to decimal
number
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

207. Example: Convert (216.857)10 = (x)7.
4
LSB
6
2
MSB
7 216
7 30
7 4
0
(216)10  (426)7
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

208. Example: Now fraction part (0.857)10 = (x)7
(216.857)10 = (426.6)7
0.857 X 7 = 5.999 5 5
0.999 X 7 = 6.993 6 6
0.993 X 7 = 6.951 6 6
0.951 X 7 = 6.657 6 6
MSB
LSB
(0.857)10  (0.5666)7 Or
(0.857)10  (0.6)7
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

209. Example: Given that (16)10 = (100)b. Find the value of b.
Sol: 16 = 1 x b2
+ 0 x b1
+ 0 x b0
16 = b2
+ 0 + 0
16 = b2
b = 4
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

210. Example:
Guneet Kaur
G
u
n
e
e
t
K
a
u
r

211. Thank You
Guneet Kaur
G
u
n
e
e
t
K
a
u
r