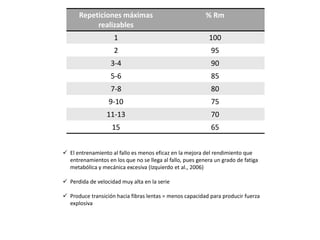
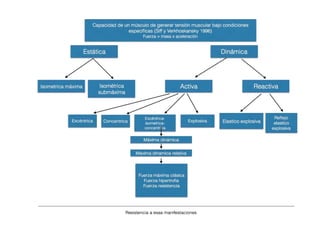
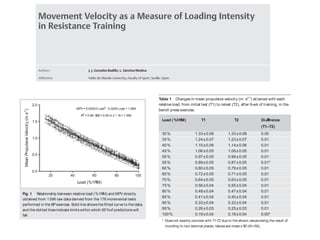
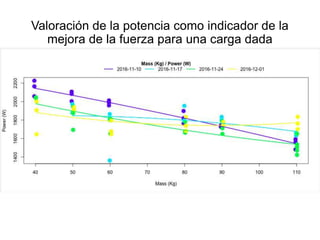
1. Training to failure is less effective for improving performance than training that does not reach failure, as it produces excessive metabolic and mechanical fatigue. 2. Reaching failure results in a very high loss of speed in the series and a transition to slower fiber types, reducing explosive force production capacity. 3. When assessing power, the goal is to improve velocity at a given load to increase power, not just improve absolute power, which is not a direct indicator of performance improvement. All training is focused on improving execution speed or explosive strength.

1. ¿ES NECESARIO VALORAR
LA RM?
¿ES NECESARIO ENTRENAR
AL FALLO?

2.  El entrenamiento al fallo es menos eficaz en la mejora del rendimiento que
entrenamientos en los que no se llega al fallo, pues genera un grado de fatiga
metabólica y mecánica excesiva (Izquierdo et al., 2006)
 Perdida de velocidad muy alta en la serie
 Produce transición hacia fibras lentas = menos capacidad para producir fuerza
explosiva
Repeticiones máximas
realizables
% Rm
1 100
2 95
3-4 90
5-6 85
7-8 80
9-10 75
11-13 70
15 65

3. ¡A jugar!
Fuerza explosiva
Fuerza-velocidad
Fuerza resistencia

5. FUERZA MAXIMA = MASA X
ACELERACIÓN

6. POTENCIA = FUERZA X
VELOCIDAD
La mejora de la potencia en términos
absolutos no es un indicador de la mejora
del rendimiento
Nos interesa la mejora de la potencia ante
una misma carga, o lo que es lo mismo, solo
nos interesa mejorar el factor velocidad
dejando intacto el factor fuerza (la carga) en
la ecuación P=F x V.
Todo entrenamiento esta enfocado a la
mejora de la velocidad de ejecución o fuerza
explosiva

7. Fuerza explosiva o Rate of Force
Development (RFD), es la producción de
fuerza en la unidad de tiempo, es decir, la
rapidez con la que se genera una
determinada cantidad de fuerza

8. twice the
from T1 to
with each
3.6%; 95 %
centage of
between m
nificant co
positive, bu
found whe
ences in m
−− Fig. 3 pr
three repr
subject wh
V1RM in T
(0.14m ·s−
remained
who showe
T1 to T2. H
V1RM in T2
both cons
0.75 m ·s− 1
were lowe
are shown
(1RM valu
this subjec
very simila
sions (0.73
in T1 and T
Stability i
individua
In order to
was depen
ranked acc
sample of
group 1 (G
RSR − 1.09
(G4), n =43
0.5
0.0
20 40 60
Load (%1RM)
MeanPropuls
80 100
Fig. 1 Relationship between relative load (%1RM) and MPV directly
obtained from 1596 raw data derived from the 176 incremental tests
performed in the BPexercise. Solid line shows the fitted curve to the data,
and the dotted lines indicate limits within which 95%of predictionswill
fall.
Table 1 Changes in mean propulsive velocity (m ·s− 1
) attained with each
relative load, from initial test (T1) to retest (T2), after 6-wk of training, in the
bench pressexercise.
Load ( %1RM) T1 T2 Difference
(T1–T2)
30% 1.33±0.08 1.33±0.08 0.00
35% 1.24±0.07 1.23±0.07 0.01
40% 1.15±0.06 1.14±0.06 0.01
45% 1.06±0.05 1.05±0.05 0.01
50% 0.97±0.05 0.96±0.05 0.01
55% 0.89±0.05 0.87±0.05 0.01*
60% 0.80±0.05 0.79±0.05 0.01
65% 0.72±0.05 0.71±0.05 0.01
70% 0.64±0.05 0.63±0.05 0.01
75% 0.56±0.04 0.55±0.04 0.01
80% 0.48±0.04 0.47±0.04 0.01
85% 0.41±0.04 0.40±0.04 0.01
90% 0.33±0.04 0.32±0.04 0.01
95% 0.26±0.03 0.25±0.03 0.01
100% 0.19±0.04 0.18±0.04 0.00*
* Doesnot exactly coincide with T1-T2 due to the shown values being the result of
rounding to two decimal places. Values are mean±SD (N=56).
Training & Testing 349
imal strength. From T1 to T2, the mean 1RM value improved by
9.3±6.7%(changing from 86.9±15.2kg to 94.5±15.2 kg). Despite
this fact, the difference in mean test velocity was only
of − 0.01±0.05 m ·s− 1
or, when expressed as absolute values, of
0.02 ±0.02m ·s− 1
, changing from 0.78±0.05m ·s− 1
to 0.76 ±
0.05 m ·s− 1
. −− Table 1 shows the differences in MPV attained
w ith each percentage of 1RM for the 56 subjects who performed
tw ice the BP test. Despite the observed change in 1RM values
from T1 to T2, after 6-wk of training, mean ICCfor MPV attained
w ith each load ( %1RM) was 0.87 (range: 0.81–0.91; CV: 0.0–
3.6%; 95%confidence interval: 0.68–0.95). When plotting per-
centage of change in the 1RM values against the differences
between mean test velocity from T1 to T2, a negative and sig-
nificant correlation could be identified (r =− 0.42, P<0.01). A
positive, but non-significant, correlation (r =0.23, P=0.091) was
found when comparing changes in V1RM from T1 to T2 and differ-
ences in mean test velocity.
−− Fig. 3 provides examples of the load-velocity relationships for
three representative subjects. −− Fig. 3a corresponds to one
subject who improved his 1RM value by 11.8 %(from 85–95 kg).
V1RM in T1 (0.16 m ·s− 1
) was almost identical to that of T2
(0.14 m ·s− 1
), while MPV with each %1RM and mean test velocity
remained stable. −− Fig. 3b shows an extreme case, the subject
2.0
1.5
1.0
0.5
0.0
20 40 60
Load (%1RM)
MPV = 0.00003 Load2
-0.0204 Load + 1.889
R2
= 0.98; SEE= 0.06 m s-1; N = 1.596
MeanPropulsiveVelocity(ms-1
)
80 100
Fig. 1 Relationship between relative load (%1RM) and MPV directly
obtained from 1596 raw data derived from the 176 incremental tests
performed in the BPexercise. Solid line showsthe fitted curve to the data,
and the dotted linesindicate limitswithin which 95%of predictions will
fall.
Table 1 Changesin mean propulsive velocity (m ·s− 1
) attained with each
htedmaterial.

9. ¿Cómo lo valoramos?
BARSENSEPOWERLIFT
ENCODER LINEAL
IRON PATH

10. Valoración de la potencia como indicador de la
mejora de la fuerza para una carga dada