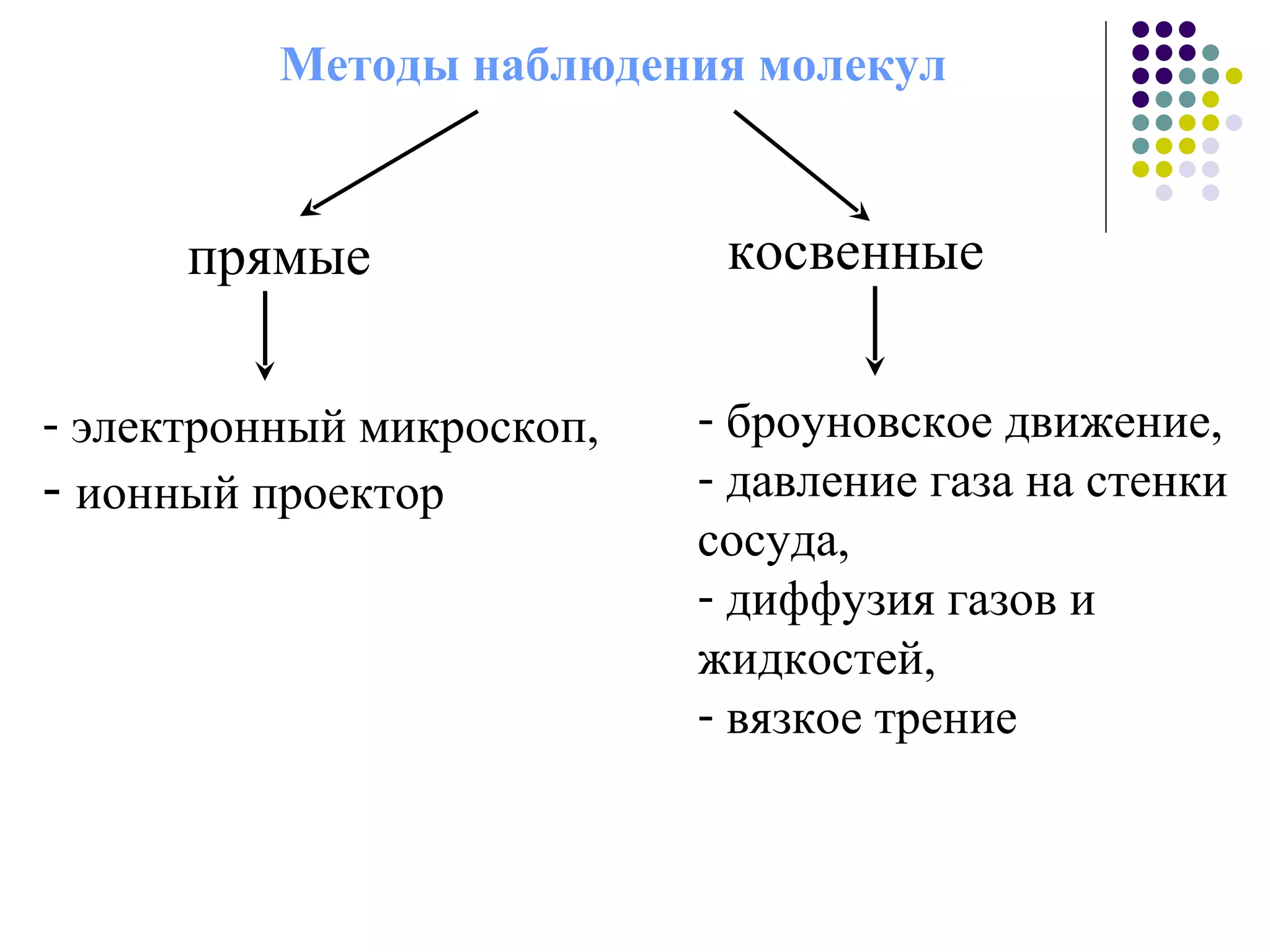
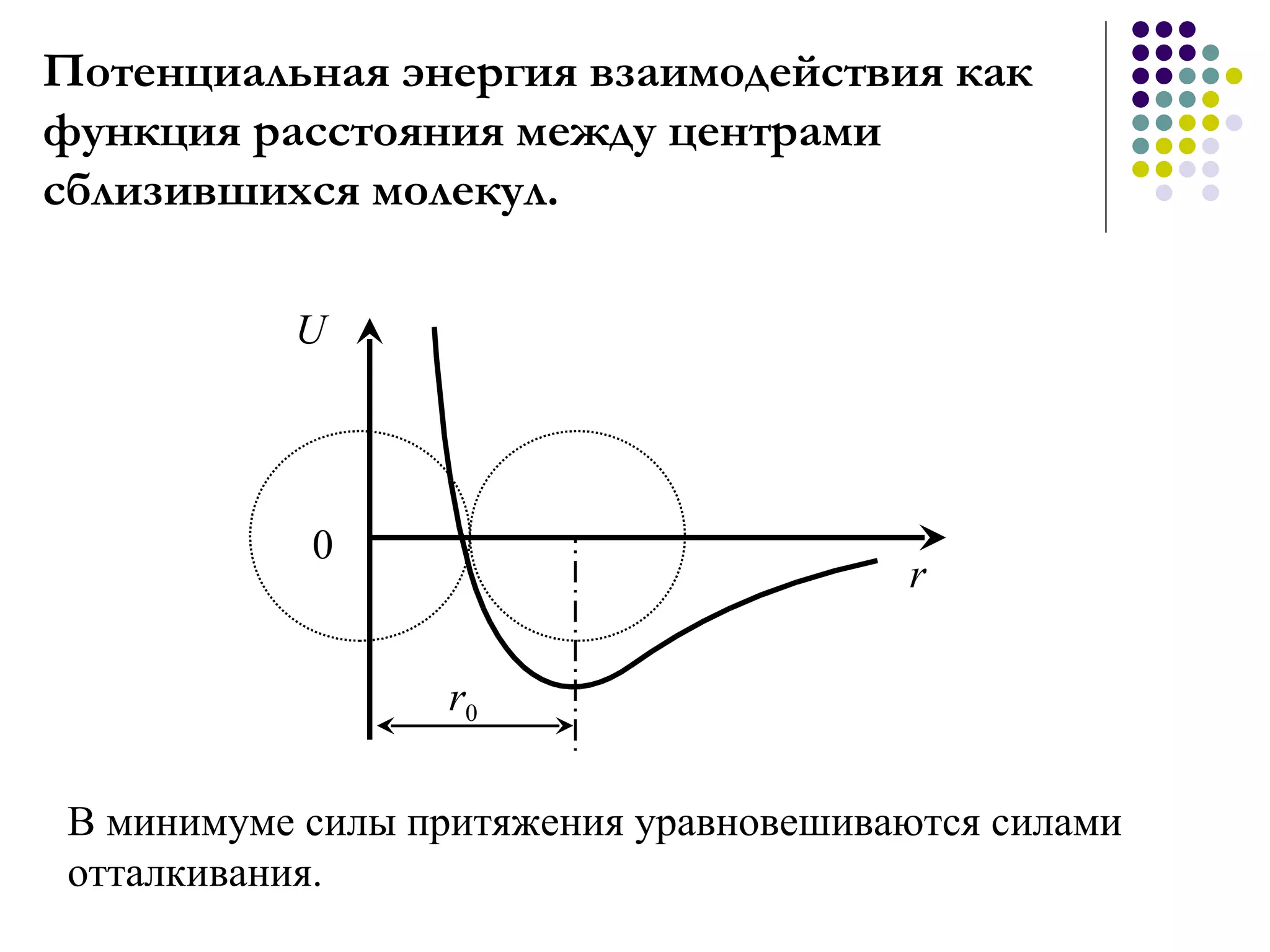
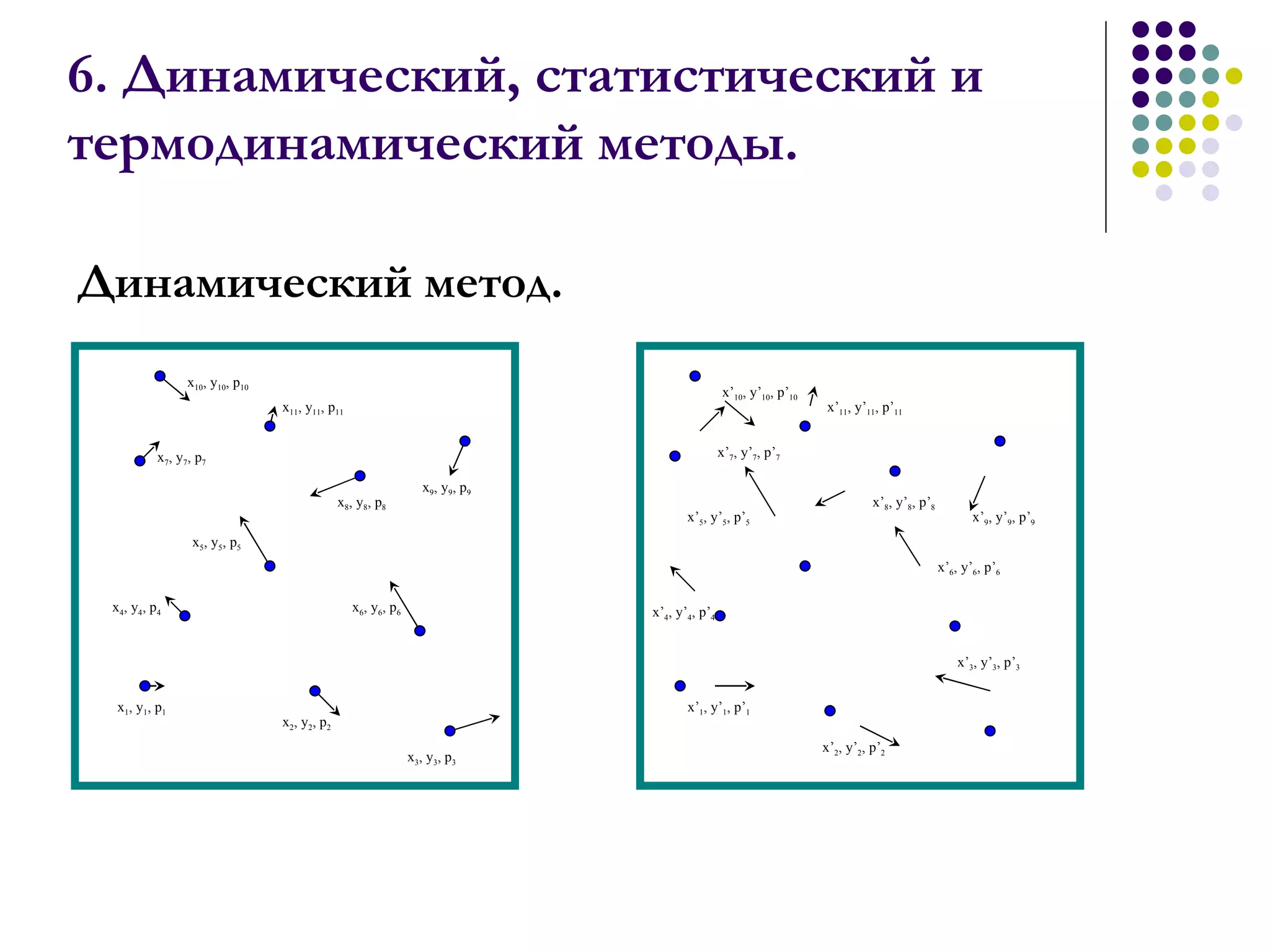
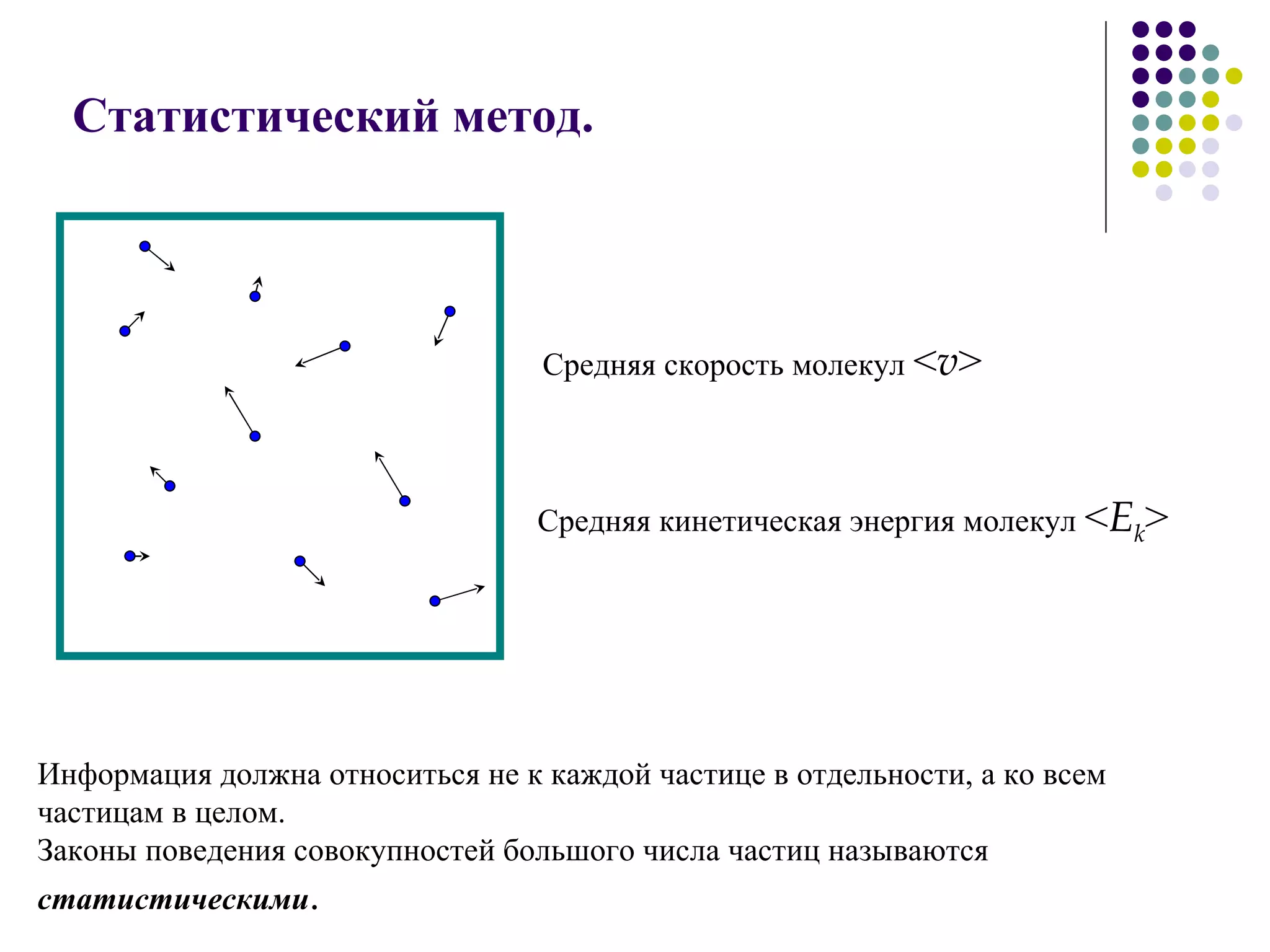
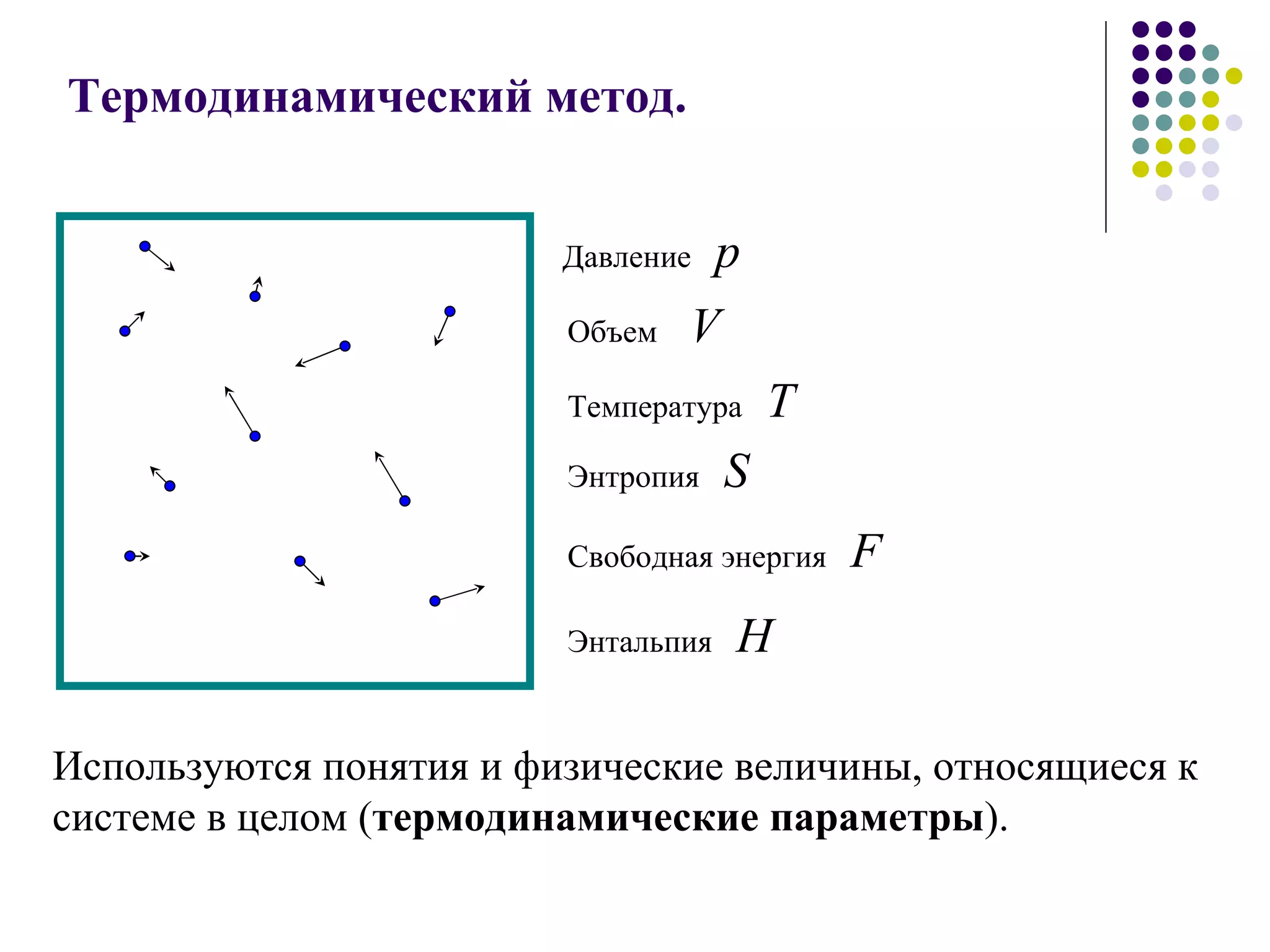
Документ посвящен основам молекулярной физики, включая статистическую физику и термодинамику. Рассматриваются методы наблюдения молекул, характеристики массы и размеров атомов, количество вещества, агрегатные состояния и модель идеального газа. Также отмечено использование динамических, статистических и термодинамических методов для анализа систем многих частиц.

1. МОЛЕКУЛЯРНАЯ ФИЗИКА. СТАТИСТИЧЕСКАЯ ФИЗИКА И ТЕРМОДИНАМИКА.

2. Лекция №1. Методы рассмотрения систем многих частиц. Предмет молекулярной физики. Масса и размеры атомов и молекул. Количество вещества. Агрегатные состояния веществ. Признаки агрегатных состояний. Модель идеального газа. Динамический, статистический и термодинамический методы.

3. Литература. Савельев И.В. Курс общей физики. – Т.1. – М., 1987. Гершензон Е.М., Малов Н.Н. Курс общей физики. Молекулярная физика. – М., 1987. Матвеев А.Н. Молекулярная физика. – М., 1987. Трофимова Т.И. Курс физики. – М., 2001.

4. 1. Предмет молекулярной физики. Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества исходя из так называемых молекулярно-кинетических представлений. Согласно этим представлениям: Любое тело – твердое, жидкое или газообразное состоит из большого числа обособленных частиц – молекул. Молекулы всякого вещества находятся в беспорядочном, не имеющим какого-либо преимущественного направления движении. В настоящее время существует ряд методов, которые позволяют как непосредственно наблюдать молекулы и атомы, таки косвенно обнаружить их наличие.

5. Методы наблюдения молекул прямые косвенные электронны й микроскоп, ионн ый проектор броуновско е движени е , давлени е газа на стенки сосуда, диффузи я газов и жидкостей, вязко е трени е

6. Броуновское движение

7. Электронный микроскоп Электронный микроскоп Поверхность куриного яйца под электронным микроскопом

8. 2. Масса и размеры атомов и молекул. В молекулярной физике принято характеризовать массы атомов и молекул не их абсолютными значениями, а относительными безразмерными величинами: относительной атомной массой А r относительной молекулярной массой М r В качестве единичной атомной массы принимается 1/12 массы изотопа углерода 12 С:

9. Относительная молекулярная масса есть масса молекулы, выраженная в а.е.м. Абсолютные значения атомных масс составляют около 10 -25 –10 -27 кг, а относительные значения 1–100. Для крупных молекул, состоящих из большого числа атомов относительная молекулярная масса порядка несколько сотен тысяч. Относительная атомная масса есть масса атома, выраженная в а.е.м.

10. 3. Количество вещества. В молекулярной физике часто используют понятие количество вещества. В СИ количество вещества выражается в молях. легко видеть, что Таким образом, моль любого вещества содержит одинаковое число структурных элементов. Это число называют постоянной Авогадро : Моль равен количеству вещества рассматриваемой системы, которое содержит столько же структурных элементов, сколько структурных элементов (атомов) содержится в 0,012 кг изотопа углерода 12 С.

11. В молекулярной физике часто используется понятие молярной массы Молекулярная и молярная массы связаны между собой простым соотношением: Число молей связано с числом структурных элементов N при помощи соотношения: Молекулярная масса с достаточной степенью точности может быть вычислена сложением атомных масс, входящих в состав молекулы атомов.

12. Пример. Рассчитаем из простых соотношений размер атома ртути. Будем полагать, что атомы ртути вплотную соприкасаются друг с другом в жидком состоянии. К онцентрация Величина обратная концентрации, т.е. показывает какой объем приходится на один атом (или молекулу) Плотность

13. Диаметр молекулы можно найти из следующих соображений:

14. 4. Агрегатные состояния веществ. Признаки агрегатных состояний. Между атомами и молекулами действуют как силы взаимного притяжения, так и отталкивания. Атомы и молекулы находятся в непрерывном хаотическом движении и, следовательно, обладают кинетической энергией. Силы притяжения стремятся связать атомы или молекулы в единое целое, а наличие кинетической энергии этому препятствует. Если потенциальная энергии притяжения по абсолютной величине много больше кинетической энергии, то вещество находится в твердом состоянии, если много меньше – то в газообразном. Жидкое состояние реализуется при примерном равенстве этих энергий.

15. Потенциальная энергия взаимодействия как функция расстояния между центрами сблизившихся молекул. В минимуме силы притяжения уравновешиваются силами отталкивания. r 0 U r 0

16. В газообразном состоянии вещество не сохраняет ни формы, ни объема. Большую часть времени каждая молекула движется без взаимодействия, затем в небольшой области, в результате столкновения с другой молекулой меняет направление движения. Расстояние пролетаемое молекулой между соударениями в сотни и тысячи раз больше диаметра самой молекулы.

17. Движение молекул в твердых, жидких и газообразных телах

18. В твердом состоянии вещество сохраняет и форму и объем. При деформации возникают силы, препятствующие изменению объема и формы. Молекулы или атомы располагаются в определенных местах и образуют кристаллическую решетку. Они колеблются около средних положений, называемых узлами кристаллической решетки. Линия, вдоль которой происходят колебания, и амплитуда колебаний медленно меняются со временем. Вдоль некоторой линии совершается достаточно много колебаний, прежде чем направление колебаний изменится.

19. Жидкое состояние характеризуется тем, что вещество стремится сохранить объем, но не сохраняет формы. Молекулы в жидкости находятся близко друг к другу, но их положения не фиксированы и они сравнительно медленно их меняют друг относительно друга. Иногда молекулы объединяются в агрегаты, состоящие из большого числа молекул, причем их агрегатное расположение определенным образом упорядоченно.

20. 5. Модель идеального газа. Наиболее простой моделью системы многих частиц является модель идеального газа. Это газ, состоящий из точечных материальных частиц, между которыми отсутствуют силы, действующие на расстоянии. Эти частицы сталкиваются между собой по законам соударения шаров, так что в результате удара изменяются абсолютные величины скоростей частиц. Наиболее близко свойствам идеального газа соответствуют достаточно разреженные газы.

21. 6. Динамический, статистический и термодинамический методы. Динамический метод. x 7 , y 7 , p 7 x 11 , y 11 , p 11 x 10 , y 10 , p 10 x 8 , y 8 , p 8 x 9 , y 9 , p 9 x 5 , y 5 , p 5 x 6 , y 6 , p 6 x 4 , y 4 , p 4 x 3 , y 3 , p 3 x 2 , y 2 , p 2 x 1 , y 1 , p 1 x’ 7 , y’ 7 , p’ 7 x’ 11 , y’ 11 , p’ 11 x’ 10 , y’ 10 , p’ 10 x’ 8 , y’ 8 , p’ 8 x’ 9 , y’ 9 , p’ 9 x’ 5 , y’ 5 , p’ 5 x’ 6 , y’ 6 , p’ 6 x’ 4 , y’ 4 , p’ 4 x’ 3 , y’ 3 , p’ 3 x’ 2 , y’ 2 , p’ 2 x’ 1 , y’ 1 , p’ 1

22. Пример. Для записи положений и скоростей всех молекул в этом объеме нужно зафиксировать 16,2·10 19 чисел. N L = 2,7·10 19 молекул ( число Лошмидта ). Количество молекул в 1 см 3 при н.у. Суперкомпьютер в Лаборатории моделирования Земли (Япония) производит 40·10 12 операций в сек. Для фиксации такого массива чисел ему нужно 47 дней! Для вычисления кинет. энергии всех молекул – 191 день! И еще 15 дней на фиксацию значений энергии. Каждая молекула испытывает примерно 10 9 столкновений в секунду. Если изменить направление скорости одной молекулы, то уже через 10 -7 с изменятся скорости 10 30 молекул, т.е. всех в нашем объеме 1 см 3 и неоднократно. динамический метод непригоден для описания реальных систем с большим числом частиц.

23. Статистический метод. Информация должна относиться не к каждой частице в отдельности, а ко всем частицам в целом. Законы поведения совокупностей большого числа частиц называются статистическими . Средняя скорость молекул < v > Средняя кинетическая энергия молекул < E k >

24. Термодинамический метод. Используются понятия и физические величины, относящиеся к системе в целом ( термодинамические параметры ). Давление p Объем V Температура T Энтропия S Свободная энергия F Энтальпия H

25. Статистический и термодинамический методы взаимно дополняют друг друга. Термодинамический метод характеризуется своей общностью и позволяет изучать явления без знания их внутренних механизмов. Статистический метод помогает понять суть явлений, установить связь поведения системы в целом с поведением и свойствами отдельных частиц и подсистем. Комбинированное применение того и другого методов способствует наиболее эффективному решению научной проблемы. Вывод: