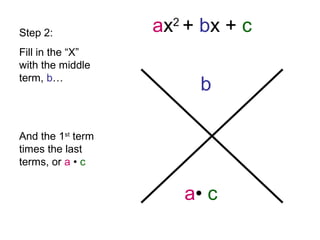
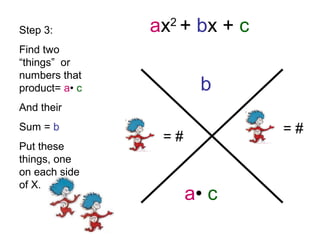
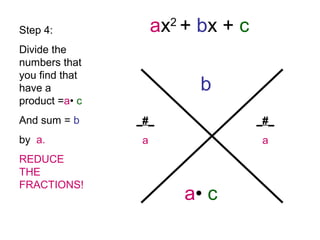
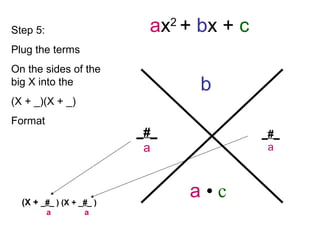
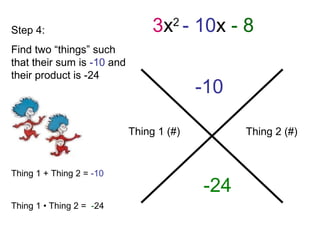
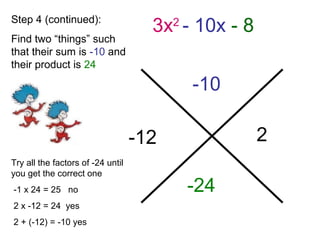
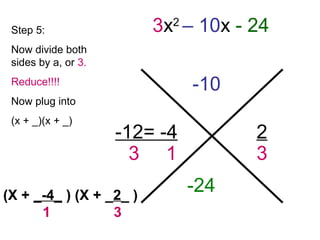
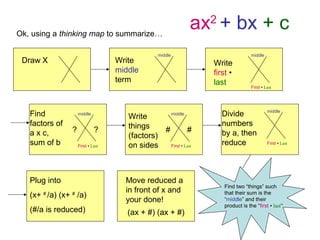
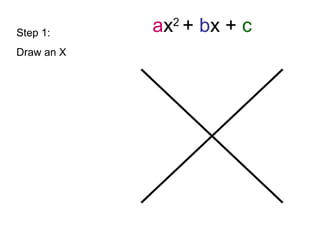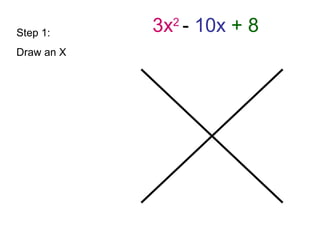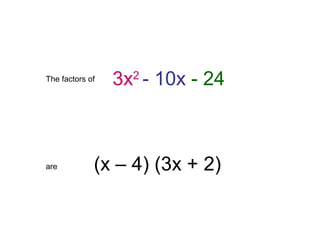The document provides step-by-step instructions for factorizing a quadratic trinomial using the grouping method. The method involves: 1) drawing an X and writing the middle and first times last terms; 2) finding two factors whose sum is the middle term and product is the first times last; 3) writing the factors on either side of the X and dividing by the leading coefficient; 4) plugging the factors into the (x + )(x + ) format and moving the denominator in front of the x terms. When completed, the factorization is obtained.

1. WARM UPS
Multiply by distribution or FOIL
method
1) (x + 2)(x + 4) 2)(x – 3)(2x + 4)
3) x2
– x – 6 4) x2
+ 7x + 12
Factor using grouping method

2. California
Standards
14.0 Students solve a quadratic
equation by factoring or completing the
square.
23.0 Students apply quadratic
equations to physical problems, such
as the motion of an object under the
force of gravity.

3. ax2
+ bx + cStep 1:
Draw an X

4. ax2
+ bx + cStep 2:
Fill in the “X”
with the middle
term, b…
And the 1st
term
times the last
terms, or a • c
b
a• c

5. ax2
+ bx + cStep 3:
Find two
“things” or
numbers that
product= a• c
And their
Sum = b
Put these
things, one
on each side
of X.
b
a• c
= #
= #

6. ax2
+ bx + cStep 4:
Divide the
numbers that
you find that
have a
product =a• c
And sum = b
by a.
REDUCE
THE
FRACTIONS!
b
a• c
_#_
a
_#_
a

7. ax2
+ bx + cStep 5:
Plug the terms
On the sides of the
big X into the
(X + _)(X + _)
Format
b
a • c
_#_
a
(X + _#_ ) (X + _#_ )
a a
_#_
a

8. ax2
+ bx + cStep 6:
Move the
denominator in front
of the X for both
terms. This is your
factorization of the
trinomial
(X + _#_ ) (X + _#_ )
a a
(aX + _#_ ) (aX + _#_ )
NOTE that the number in front of the x may not
equal a since we reduced the fraction in step 5.

9. We don’t get
it…can you
show us?

10. 3x2
- 10x + 8Step 1:
Draw an X

11. Step 2:
Fill in the “X” with
the middle term,
-10…
And the 1st
term
times the last
terms, or 3 • -8
-10
3 • -8 = -24
3x2
- 10x - 8
-24

12. Step 4:
Find two “things” such
that their sum is -10 and
their product is -24
Thing 1 + Thing 2 = -10
Thing 1 • Thing 2 = -24
3x2
- 10x - 8
-10
-24
Thing 1 (#) Thing 2 (#)

13. Step 4 (continued):
Find two “things” such
that their sum is -10 and
their product is 24
Try all the factors of -24 until
you get the correct one
-1 x 24 = 25 no
2 x -12 = 24 yes
2 + (-12) = -10 yes
-12
3x2
- 10x - 8
-10
-24
2

14. -12= -4
3x2
– 10x - 24
-10
-24
2
Step 5:
Now divide both
sides by a, or 3.
Reduce!!!!
Now plug into
(x + _)(x + _)
3 3
(X + _-4_ ) (X + _2_ )
1 3
1

15. ax2
+ bx + cStep 6:
Move the
denominator in front
of the X for both
terms. This is your
factorization of the
trinomial
(X - _4_ ) (X + _2_ )
1 3
(1X - 4 ) (2X + 3 )
NOTE that the number in front of the x may not
equal a since we reduced the fraction in step 5.

16. The factors of
are
3x2
- 10x - 24
(x – 4) (3x + 2)

17. Ok, using a thinking map to summarize…
Draw X Write
middle
term
Write
first •
last
middle
middle
First • Last
Find
factors of
a x c,
sum of b
Write
things
(factors)
on sides
Divide
numbers
by a, then
reduce
Find two “things” such
that their sum is the
“middle” and their
product is the “first • last”
ax2
+ bx + c
middle
First • Last
? ?
middle
First • Last
# #
Plug into
(x+ #
/a) (x+ #
/a)
(#/a is reduced) (ax + #) (ax + #)
middle
First • Last
Move reduced a
in front of x and
your done!