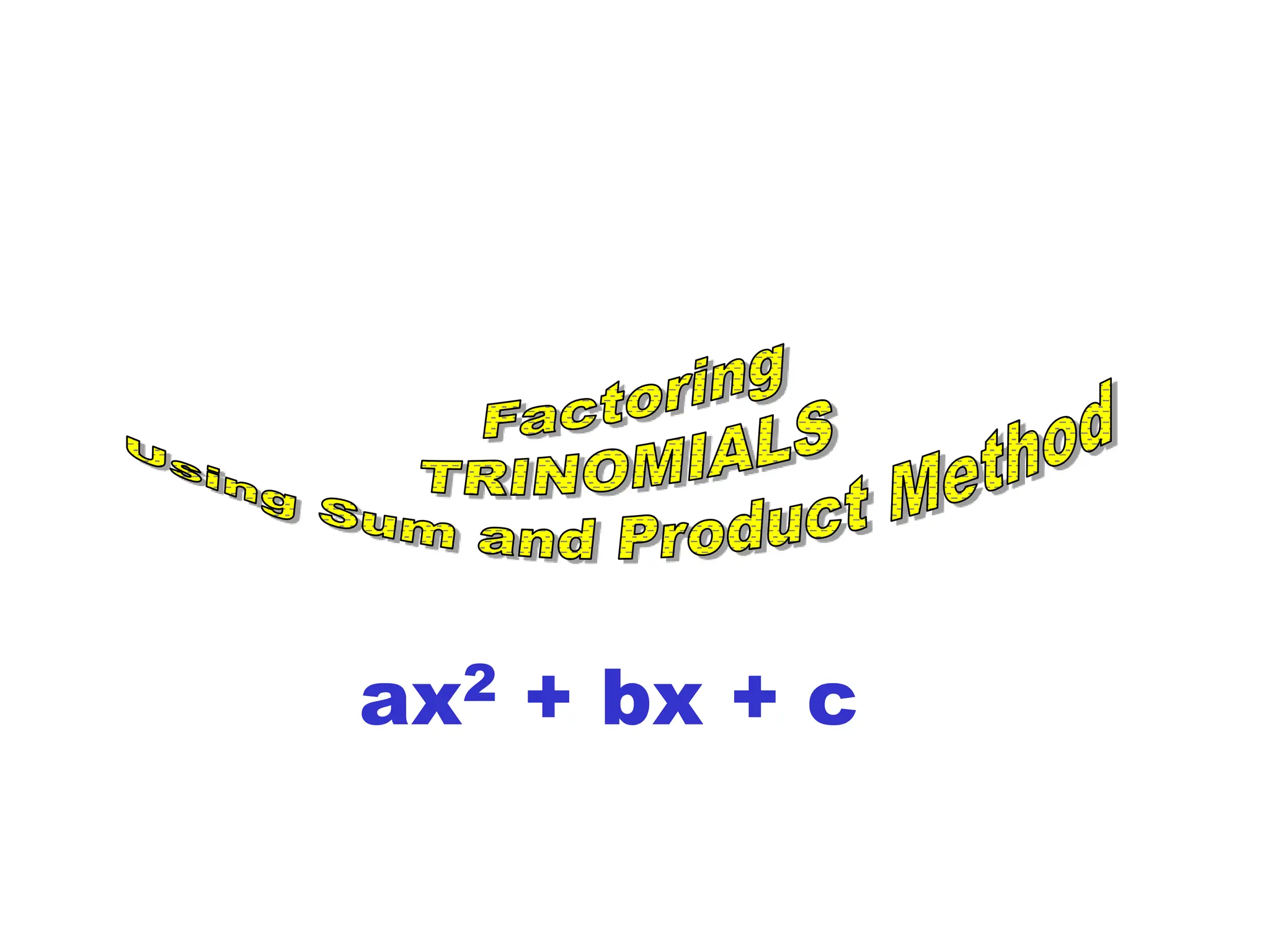
This document provides examples and instructions for factoring trinomials of the form ax2 + bx + c. It explains that the factors of c must have a sum of b and a product of ac. Several examples are worked through step-by-step to show how to set up a "MAMA table" to find the appropriate factors and then group the terms of the trinomial accordingly. The document also discusses how the signs of the factors change depending on the signs of b and c. Rules for determining the signs in different cases are presented.

1. ax2 + bx + c

2. Example 1: x2 + 11x + 24
Their sum equals the middle term (b) of the trinomial.
When factoring these trinomials the factors will be
two binomials: (x + )(x + )
We know that the first terms of each binomial must
be x because the first term of the trinomial is x2 and
x  x = x2. The challenge is to find the last term of
each binomial. They must be chosen so that they
will cause the coefficient of the middle term and
the last term of the trinomial to work out.
(That’s 11 and 24 in this case.)
+ = 11
Their product of those same numbers equals the last
term © of the trinomial.  = 24

3. List the factors of 24:
Example 1: x2 + 11x + 24
1 24 SUM = 25
2 12 SUM = 14
3 8 SUM = 11
4 6 SUM = 10
It is the factors 3 and 8 that produce a sum of 11
AND a product of 24 so they must be the last terms
of each binomial.
(x + 3)(x + 8)
24
11

4. If we multiply these factors using FOIL, we get the
polynomial that we started with.
(x + 3)(x + 8)
= x2 + 8x + 3x + 24
(x)(x) = x2
(x)(8) = 8x
(3)(x) = 3x
(3)(8) = 24
As we look at the 4 terms above, it becomes apparent
why the sum of the last terms in each binomial must
be equal to the middle term of the trinomial.
(x + 3)(x + 8)
= x2 + 8x + 3x + 24
= x2 + 11x + 24

5. Example 2: a2 + 16a + 28
SUM = 16
a  a = a2 so they are the first terms of each binomial
and the factors 2 and 14 make a sum of 16 so the are
the last terms of each binomial.
= (a + 2)(a + 14)
28
16

6. Example 3: y2 + 2y + 1 Factors of 1:
1 1
y2 + 2y + 1
= (y + 1)(y + 1)
= (y + 1)(y + 1)
Factors of 1:
1 1
Sometimes there is only 1 pair of
factors to consider.
Example 4: m2 + 3m + 1
Factors of 1:
1 1
In this example the factors available do
not make a sum of 3 which means that the
trinomial can’t be factored.
Example 5: p2 + 23p + 120
Factors of 120:
1 120
2 60
3 40
4 30
5 24
6 20
8 15
10 12
1 120
2 60
3 40
4 30
5 24
6 20
8 15
10 12
= (p + 8)(p + 15)
= (p + 8)(p + 15)
In this example there are many pairs of
factors to consider. Most examples will
have fewer than these. The trick is in
being able to quickly find all of the factors
of c. p2 + 23p + 120
SUM = 2
SUM = 3
SUM
= 23

7. In each of the preceding examples the signs of the
terms in the trinomials were always positive. Now we
will observe examples where the signs can be negative.
Example 6: x2 + 5x + 6 Factors of 6:
1 6
2 3
SUM = 5
Factors of 6:
1 6
2 3
= (x + 2)(x + 3)
Example 7: x2 + 5x - 6 Factors of -6:
-1 +6
-2 +3
SUM = 5
When looking for the factors of a negative number, one
must be positive and the other negative. If at the same
time their sum is positive, then the factor that is bigger
must be the positive one.
-1 +6
-2 +3
= (x - 1)(x + 6)

8. REVIEW OF RULES FOR SIGNS
Sign of bigger
number
(+) + (+) = (+)
(+) + (-) =
(-) + (+) =
(-) + (-) = (-)
( )
ADDITION
(+)(+) = (+)
(+)(-) = (-)
(-)(+) = (-)
(-)(-) = (+)
MULTIPLICATION
Example 8: x2 - 5x - 6
= (x + 1)(x - 6)
When both the product and sum are
negative, the factors have opposite
signs but this time the bigger factor
will be negative.
-6
-5

9. Example 9: x2 - 5x + 6 Factors of 6:
SUM = -5
-1 -6
-2 -3
= (x - 2)(x - 3)
When looking for factors of a positive
number when the sum is negative,
both factors will be negative.
Example 10: x2 - 5x - 36 Factors of -36:
1 -36
2 -18
3 -12
4 -9
6 -6
SUM = -5
1 -36
2 -18
3 -12
4 -9
6 -6
= (x + 4)(x - 9)

10. First terms:
Outer terms:
Inner terms:
Last terms:
Combine like terms.
y2 + 6y + 8
y +2
y
+4
y2
+4y
+2y
+8
y2
+4y
+2y
+8
Review: (y + 2)(y + 4)
In this lesson, we will begin with y2 + 6y + 8 as our
problem and finish with (y + 2)(y + 4) as our answer.

11. Here we go! 1) Factor y2 + 6y + 8
Use your factoring chart.
Do we have a GCF?
Is it a Diff. of Squares problem?
Now we will learn Trinomials! You will set up
a table with the following information.
Nope!
No way! 3 terms!
Product of the first and
last coefficients
Middle
coefficient
The goal is to find two factors in the first column that
add up to the middle term in the second column.
We’ll work it out in the next few slides.

12. 1) Factor y2 + 6y + 8
Create your MAMA table.
Multiply Add
+8 +6
Product of the
first and last
coefficients
Middle
coefficient
Here’s your task…
What numbers multiply to +8 and add to +6?
If you cannot figure it out right away, write
the combinations.
M
A

13. 1) Factor y2 + 6y + 8
Place the factors in the table.
+1, +8
-1, -8
+2, +4
-2, -4
Multiply Add
+8 +6
Which has
a sum
of +6?
+9, NO
-9, NO
+6, YES!!
-6, NO
We are going to use these numbers in the next step!

14. 1) Factor y2 + 6y + 8
+2, +4
Multiply Add
+8 +6
+6, YES!!
Hang with me now! Replace the middle number of
the trinomial with our working numbers from the
MAMA table
y2 + 6y + 8
y2 + 2y + 4y + 8
Now, group the first two terms and the last two
terms.

15. We have two groups!
(y2 + 2y)(+4y + 8)
If things are done
right, the parentheses
should be the same.
Almost done! Find the GCF of each group and factor
it out.
y(y + 2) +4(y + 2)
(y + 4)(y + 2)
Tadaaa! There’s your answer…(y + 4)(y + 2)
You can check it by multiplying. Piece of cake, huh?
There is a shortcut for some problems too!
(I’m not showing you that yet…)
Factor out the
GCF’s. Write them
in their own group.

16. 2) Factor x2 – 2x – 63
Create your MAMA table.
Multiply Add
-63 -2
Product of the
first and last
coefficients
Middle
coefficient
-63, 1
-1, 63
-21, 3
-3, 21
-9, 7
-7, 9
-62
62
-18
18
-2
2
Signs need to
be different
since number
is negative.
M
A

17. Replace the middle term with our working
numbers.
x2 – 2x – 63
x2 – 9x + 7x – 63
Group the terms.
(x2 – 9x) (+ 7x – 63)
Factor out the GCF
x(x – 9) +7(x – 9)
The parentheses are the same! Weeedoggie!
(x + 7)(x – 9)

18. Here are some hints to help
you choose your factors in the
MAMA table.
1) When the last term is positive, the factors
will have the same sign as the middle term.
2) When the last term is negative, the factors
will have different signs.

19. 2) Factor 5x2 - 17x + 14
Create your MAMA table.
Multiply Add
+70 -17
Product of the
first and last
coefficients
Middle
coefficient
-1, -70
-2, -35
-7, -10
-71
-37
-17
Signs need to
be the same as
the middle
sign since the
product is
positive. Replace the middle term.
5x2 – 7x – 10x + 14
Group the terms.
M
A

20. (5x2 – 7x) (– 10x + 14)
Factor out the GCF
x(5x – 7) -2(5x – 7)
The parentheses are the same! Weeedoggie!
(x – 2)(5x – 7)
Hopefully, these will continue to get easier the
more you do them.

21. Factor x2 + 3x + 2
1. (x + 2)(x + 1)
2. (x – 2)(x + 1)
3. (x + 2)(x – 1)
4. (x – 2)(x – 1)

22. Factor 2x2 + 9x + 10
1. (2x + 10)(x + 1)
2. (2x + 5)(x + 2)
3. (2x + 2)(x + 5)
4. (2x + 1)(x + 10)

23. Factor 6y2 – 13y – 5
1. (6y2 – 15y)(+2y – 5)
2. (2y – 1)(3y – 5)
3. (2y + 1)(3y – 5)
4. (2y – 5)(3y + 1)

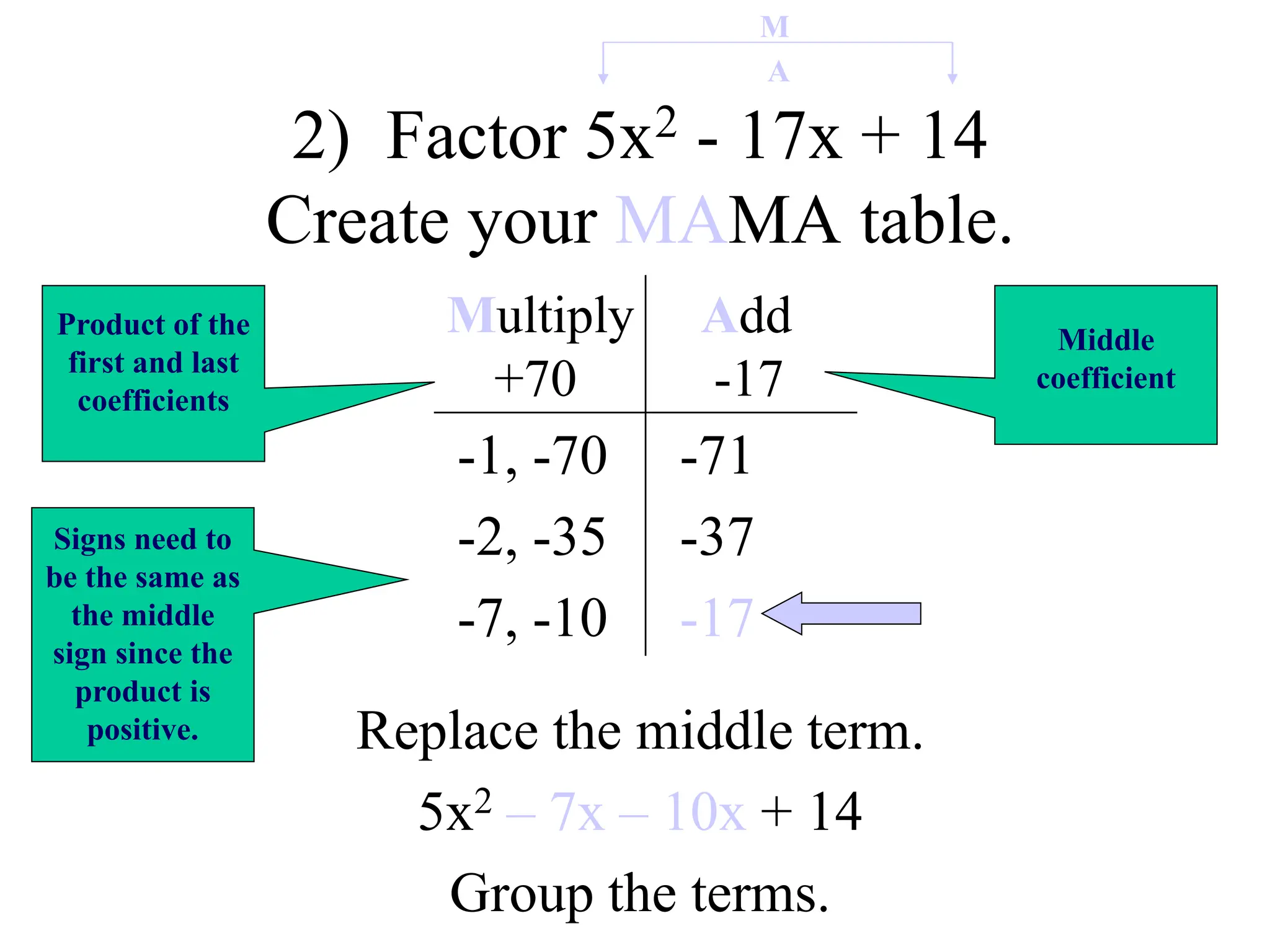
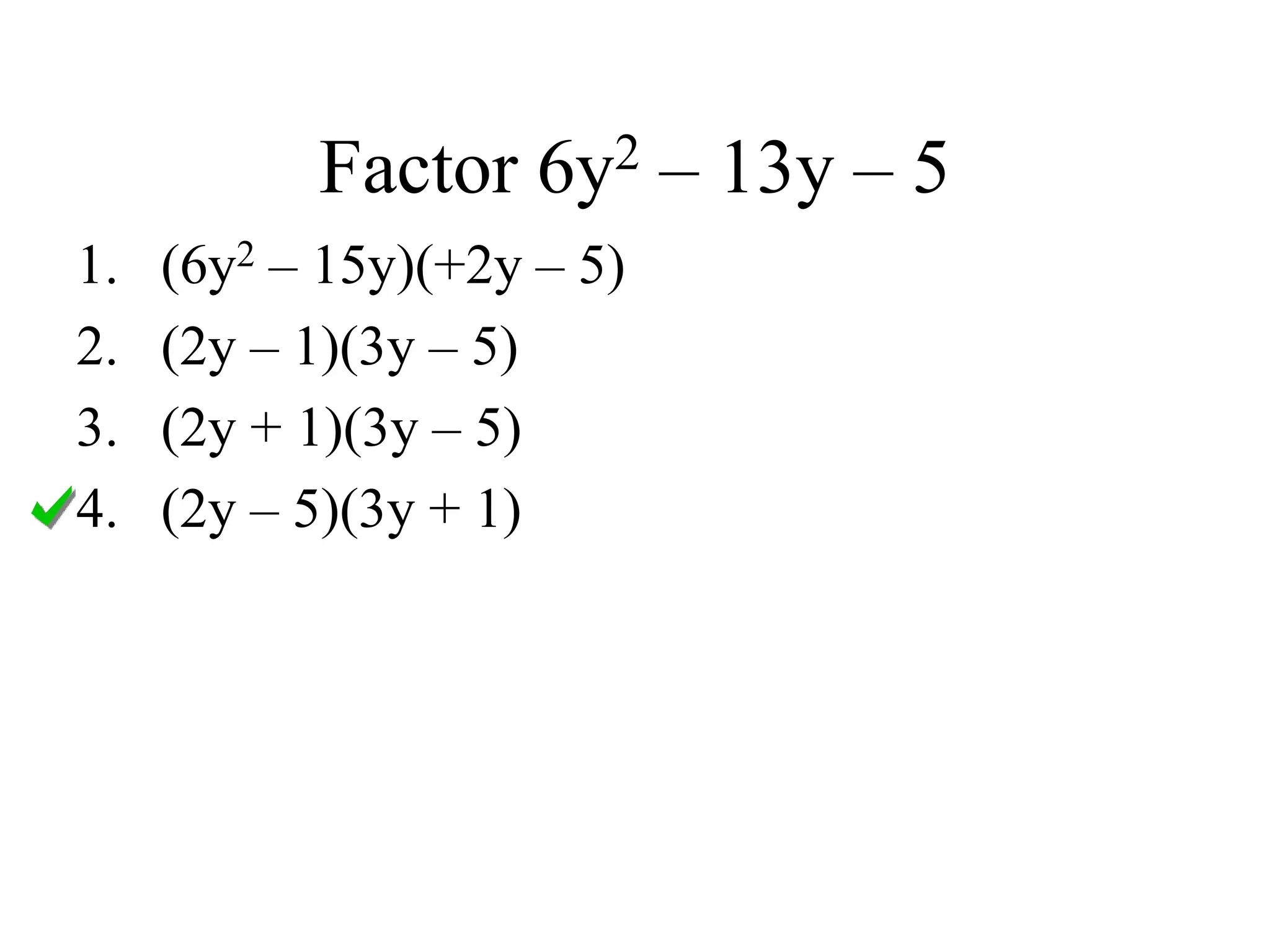
24. 2) Factor 2x2 - 14x + 12
Multiply Add
+6 -7
Find the GCF!
2(x2 – 7x + 6)
Now do the MAMA table!
-7
-5
Signs need to
be the same as
the middle
sign since the
product is
positive.
Replace the middle term.
2[x2 – x – 6x + 6]
Group the terms.
-1, -6
-2, -3

25. 2[(x2 – x)(– 6x + 6)]
Factor out the GCF
2[x(x – 1) -6(x – 1)]
The parentheses are the same! Weeedoggie!
2(x – 6)(x – 1)
Don’t forget to follow your factoring chart when
doing these problems. Always look for a GCF
first!!