Документ описывает временную сложность алгоритмов, используя o-нотацию для обозначения зависимости количества операций от входных данных. В нем также обсуждаются различные структуры данных, их операции и временная сложность для индексации, поиска, вставки и удаления. Упоминаются примеры, такие как стеки и очереди, и приводятся ссылки на ресурсы для дальнейшего изучения.






![7
Big O
[4, 6, 6, 7, 4, 7, 8, 5]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-7-320.jpg)
![8
Big O
O(n)
[4, 6, 6, 7, 4, 7, 8, 5]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-8-320.jpg)
![9
Big O
O(n)
[4, 6, 6, 7, 4, 7, 8, 5]
8
O(n/2)](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-9-320.jpg)
![10
Big O
O(n)
[4, 6, 6, 7, 4, 7, 8, 5]
8
O(n/2) 4
O( 𝑛2
)](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-10-320.jpg)
![11
Big O
O(n)
[4, 6, 6, 7, 4, 7, 8, 5]
8
O(n/2) 4
O( 𝑛2
) 64
O(2 𝑛
)](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-11-320.jpg)
![12
Big O
O(n)
[4, 6, 6, 7, 4, 7, 8, 5]
8
O(n/2) 4
O( 𝑛2
) 64
O(2 𝑛
) 256](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-12-320.jpg)












































![61
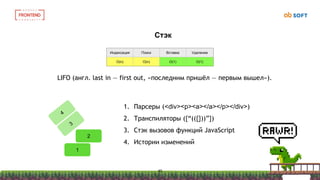
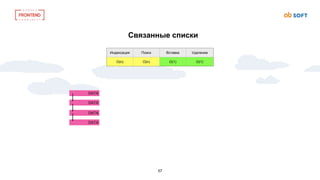
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[5, 8, 13, 6, 4, 23, 9]
54](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-61-320.jpg)
![62
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[5, 8, 13, 6, 4, 23, 9]
indexOf()/includes() - O(n)
55](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-62-320.jpg)
![Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[5, 8, 13, 6, 4, 23, 9]
indexOf()/includes() - O(n)
Hash table conversation - O(n + 1) => O(n) // O(1)
63](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-63-320.jpg)
![64
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[5, 8, 13, 6, 4, 23, 9]
indexOf()/includes() - O(n)
Binary search O(n log(n) + log(n)) => O(n log(n))
Hash table convertation - O(n + 1) => O(n) // O(1)](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-64-320.jpg)
![65
Бинарный поиск
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-65-320.jpg)
![66
Бинарный поиск
[4, 5, 6, 7, 8, 9, 13, 23]
O(n log(n))
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-66-320.jpg)
![67
Бинарный поиск
23
[4, 5, 6, 7, 8, 9, 13, 23]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-67-320.jpg)
![68
Бинарный поиск
23
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-68-320.jpg)
![69
Бинарный поиск
23
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-69-320.jpg)
![70
Бинарный поиск
23
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-70-320.jpg)
![71
Бинарный поиск
23
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]
[4, 5, 6, 7, 8, 9, 13, 23]
O(log(n))](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-71-320.jpg)

![73
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
indexOf()/includes() - O(n)
Binary search O(n log(n) + log(n)) => O(n log(n))
Hash table conversation - O(n + 1) => O(n) // O(1)
Binary search tree - O(log(n))
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-73-320.jpg)
![74
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
6
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-74-320.jpg)
![75
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
5
6
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-75-320.jpg)
![76
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
5 8
6
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-76-320.jpg)
![77
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
13
5 8
6
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-77-320.jpg)
![78
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
13
5 8
6
7
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-78-320.jpg)
![79
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
13
5 8
6
4 7
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-79-320.jpg)
![80
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
23
13
5 8
6
4 7
[6, 5, 8, 13, 7, 4, 23, 9]](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-80-320.jpg)
![81
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[6, 5, 8, 13, 7, 4, 23, 9]
9 23
13
5 8
6
4 7](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-81-320.jpg)
![82
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[6, 5, 8, 13, 7, 4, 23, 9]
9 23
13
5 8
6
4 7](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-82-320.jpg)
![83
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[6, 5, 8, 13, 7, 4, 23, 9]
9 23
13
5 8
6
4 7](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-83-320.jpg)
![84
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[6, 5, 8, 13, 7, 4, 23, 9]
9 23
13
5 8
6
4 7](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-84-320.jpg)
![85
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[6, 5, 8, 13, 7, 4, 23, 9]
9 23
13
5 8
6
4 7](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-85-320.jpg)
![86
Индексация Поиск Вставка Удаление
O(log(n)) O((log(n)) O((log(n)) O((log(n))
Бинарное дерево
[6, 5, 8, 13, 7, 4, 23, 9]
9 23
13
5 8
6
4 7](https://image.slidesharecdn.com/03-191013114747/85/JavaScript-Odessa-Frontend-Meetup-13-86-320.jpg)



