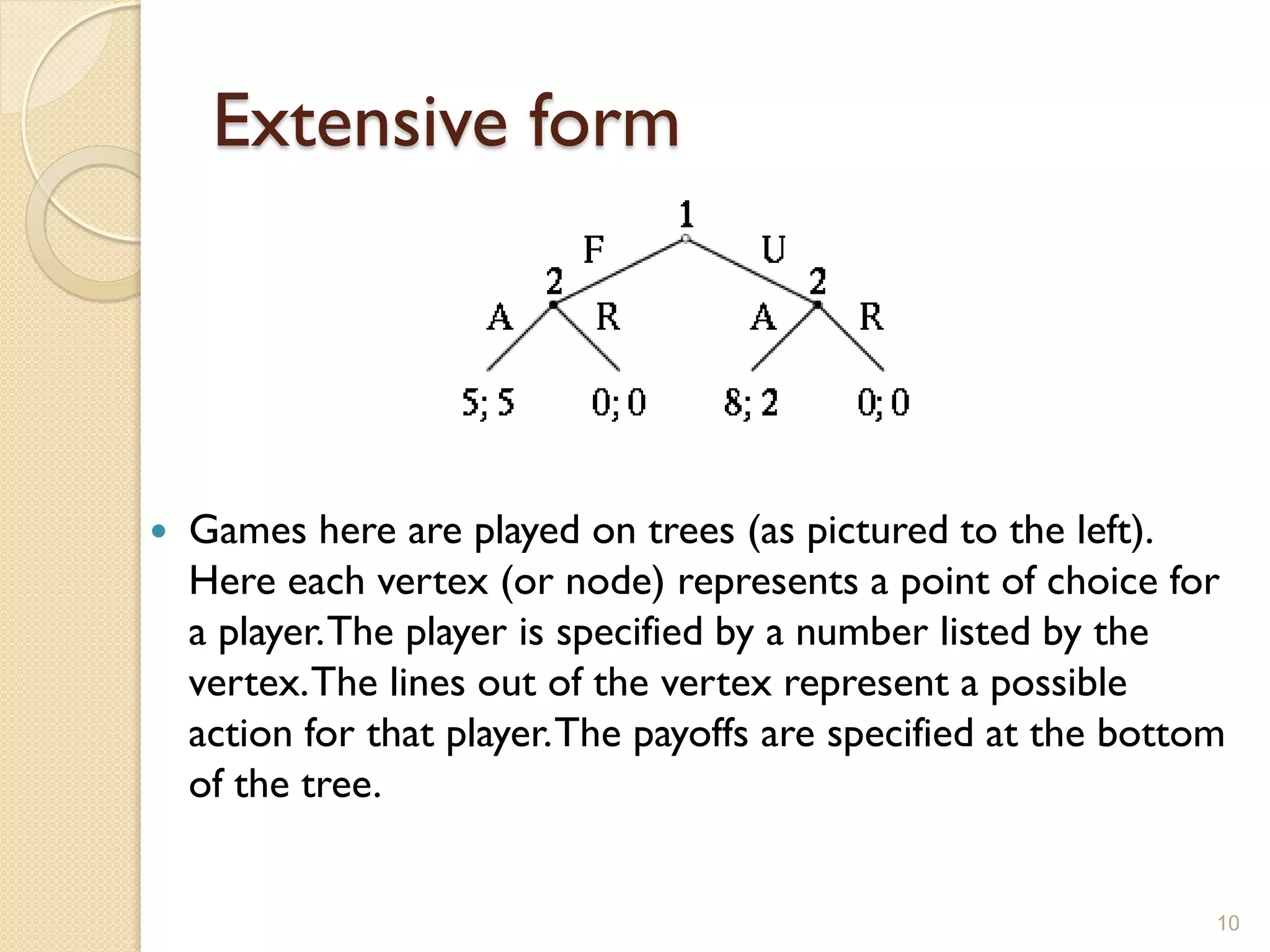
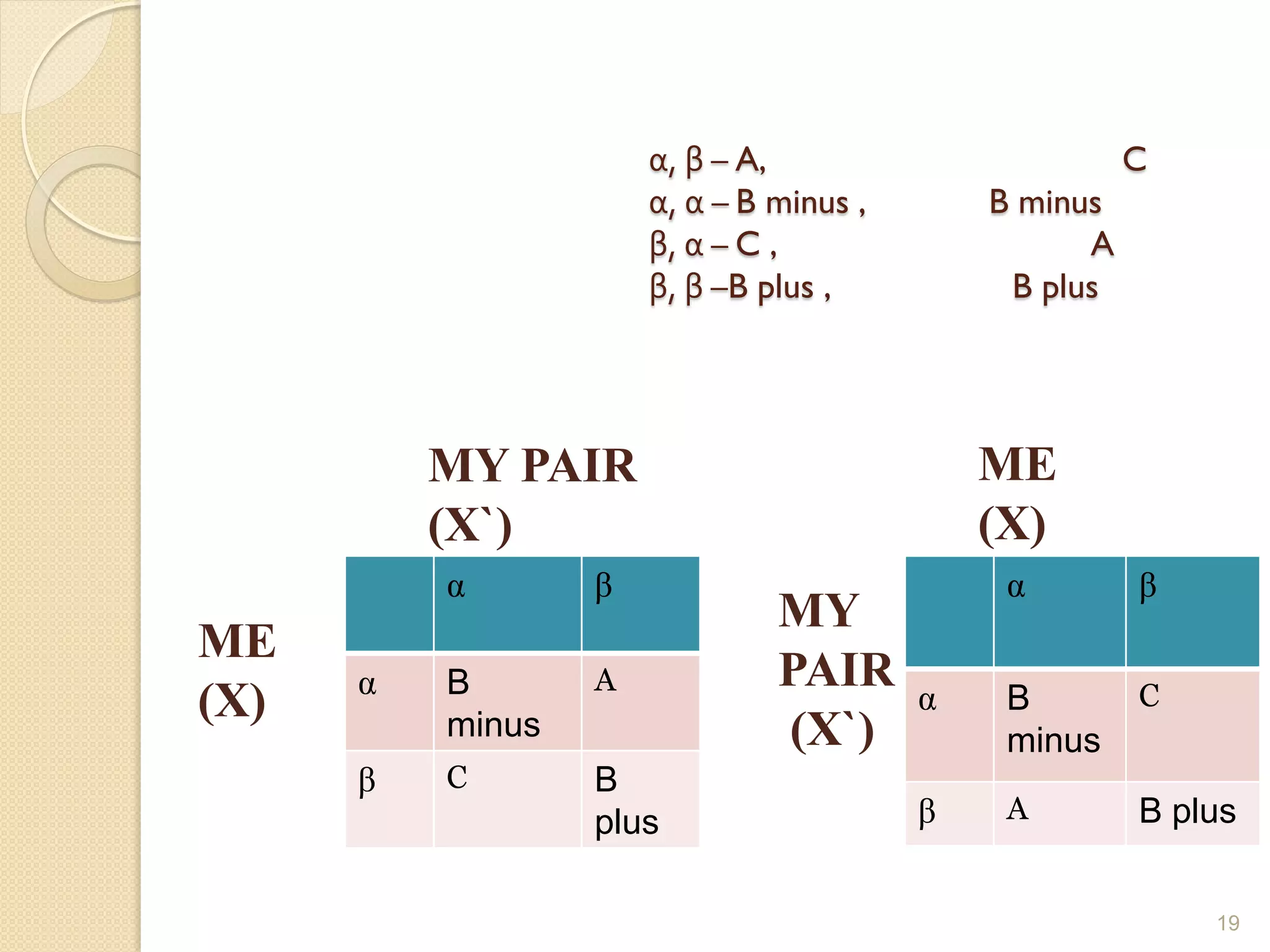
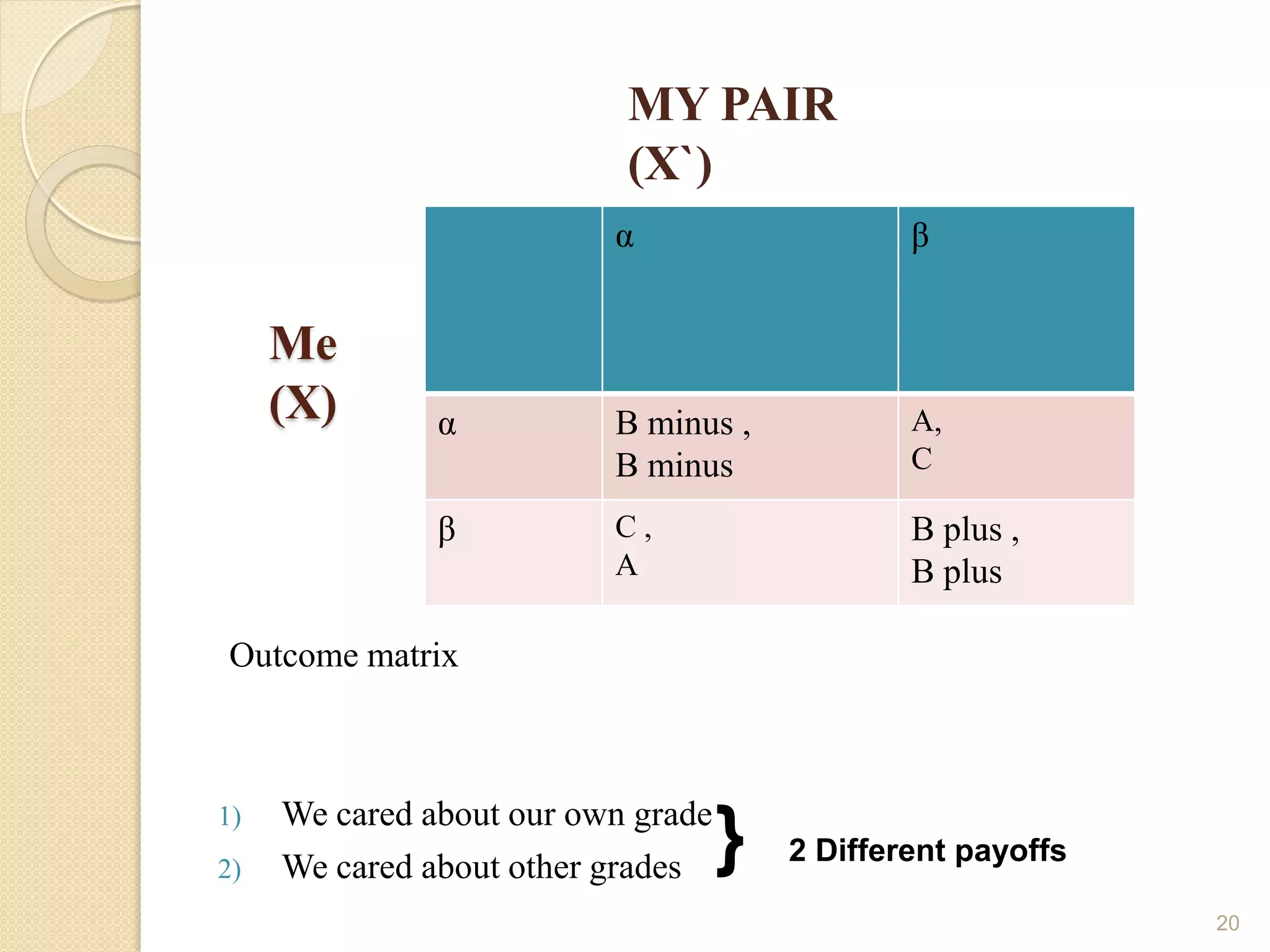
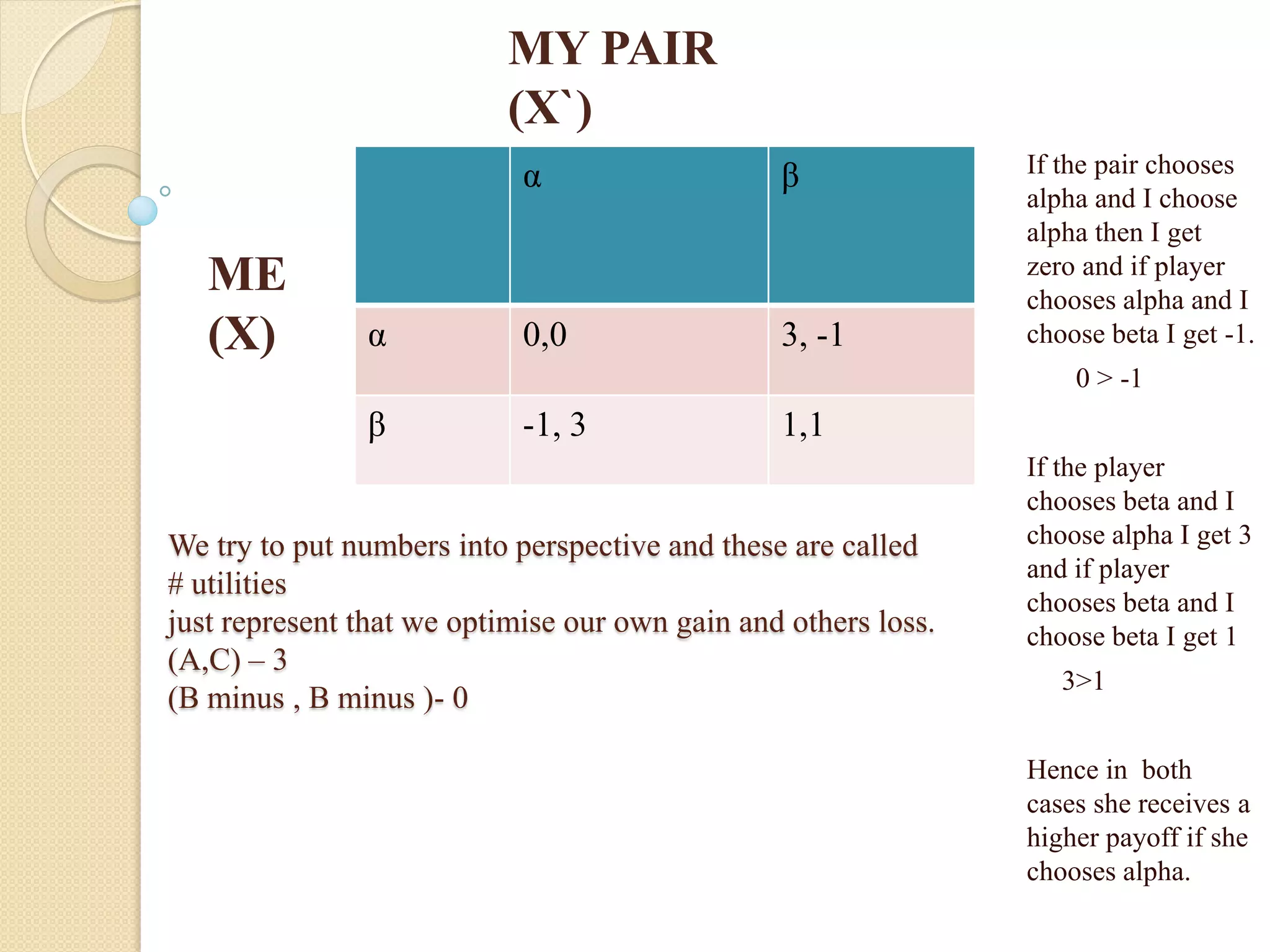
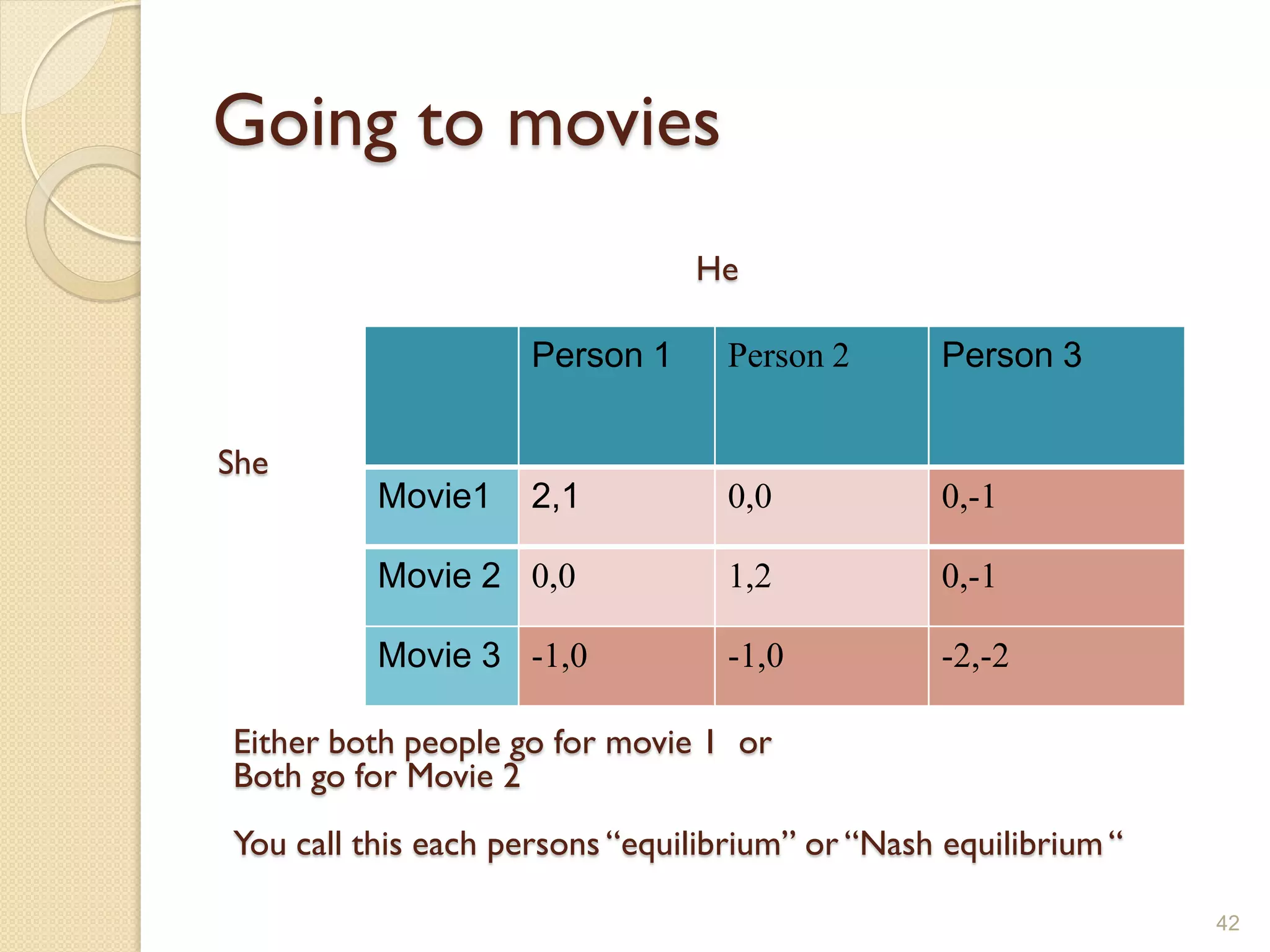
Game theory is the study of strategic decision making. It involves analyzing interactions between players where the outcome for each player depends on the actions of all players. Key concepts in game theory include Nash equilibrium, where each player's strategy is the best response to the other players' strategies, and Prisoner's Dilemma, where the non-cooperative equilibrium results in a worse outcome for both players than if they had cooperated. Game theory is applied in economics, political science, biology, and many other fields to model strategic interactions.

1. GAME THEORY

2. History
 1928 –
Game theory did not really exist as a unique field until John von Neumann &
Morgenstern published a paper.
 1950 -
John Nash developed a criterion for mutual consistency of players' strategies, known as
Nash equilibrium, applicable to a wider variety of games than the criterion proposed
by von Neumann and Morgenstern.
 1965 –
Reinhard Selten introduced his solution concept of subgame perfect equilibria, which
further refined the Nash equilibrium.
 1970 –
Game theory was extensively applied in biology, largely as a result of the work of John
Maynard Smith and his evolutionarily stable strategy.
 2007 –
Leonid Hurwicz, together with Eric Maskin and Roger Myerson, was awarded the
Nobel Prize in Economics "for having laid the foundations of mechanism
design theory
2

3. What's IT??
Game theory is a method of
studying strategic decision
making. More formally, it is "the
study of mathematical models of
conflict and cooperation
between intelligent rational
decision-makers.
Strategic- It is a setting where
the outcomes that affect you
depends on actions not just on
your own actions but on actions
of others. 3

4. Why game theory ???
Because the press tells us to …
―Managers have much to learn from game theory —provided they use it
to clarify their thinking, not as a substitute for business experience.‖
The Economist, 15 June 2007
―Game Theory, long an intellectual pastime, came into its own as a
business tool.‖
Forbes, 3 July 2009
―Game theory is hot.‖
The Wall Street Journal, 13 February 2011
Because recruiters tell us to …
―Game theory forces you to see a business situation over many
periods from two perspectives: yours and your competitor’s.‖
Judy Lewent – CFO, Merck
―Game theory can explain why oligopolies tend to be unprofitable,
the cycle of over capacity and overbuilding, and the tendency to
execute real options earlier than optimal.‖
Tom Copeland – Director of Corporate Finance, McKinsey
4

5. Terminology
 Players
 Strategies
◦ Choices available to each of the players
 Might be conditioned on history
 Payoffs
◦ Some numerical representation of the
objectives of each player
 Could take account fairness/reputation, etc.
 Does not mean players are narrowly selfish
5

6. Standard Assumptions
 Rationality
◦ Players are perfect calculators and
implementers of their desired strategy
 Common knowledge of rules
◦ All players know the game being played
 Equilibrium
◦ Players play strategies that are mutual best
responses
6

7. Strategies for Studying Games of
Strategy
 Two general approaches
◦ Case-based
 Pro: Relevance, connection of theory to application
 Con: Generality
◦ Theory
 Pro: General principle is clear
 Con: Applying it may not be
Types of firms :
1)Perfect competition
2)Monopolistic or Imperfect competition.
ex- Motor car industry , mobile markets etcetera.
7

8. Where It Exists?
An easy strategy A complex strategy
Asking your friend out for dinner? Geopolitical talks?
8

9. Representation of Games
 The games studied in game theory are well-defined
mathematical objects. A game consists of a set of players, a
set of moves (or strategies) available to those players, and
a specification of payoffs for each combination of
strategies.
 Categories :
Extensive form
Normal form
Characteristic function form
Partition function form
9

10. Extensive form
 Games here are played on trees (as pictured to the left).
Here each vertex (or node) represents a point of choice for
a player. The player is specified by a number listed by the
vertex. The lines out of the vertex represent a possible
action for that player. The payoffs are specified at the bottom
of the tree.
10

11. Normal/Strategic Form
 The normal (or strategic form) game is usually
represented by a matrix which shows the players,
strategies, and payoffs. More generally it can be
represented by any function that associates a payoff
for each player with every possible combination of
actions.
11

12. Types of Games
Cooperative :
A game is cooperative if the players are able to form binding
commitments. For instance the legal system requires them to adhere
to their promises. Often it is assumed that communication among
players is allowed in cooperative games. Cooperative games focus
on the game at large.
Non-cooperative :
In game theory, a non-cooperative game is one in which players
make decisions independently. Non-Cooperative games are able to
model situations to the finest details, producing accurate results.
Hybrid games :
contain cooperative and non-cooperative elements.
12

13. Symmetric :
A symmetric game is a game where the payoffs for playing a particular
strategy depend only on the other strategies employed, not on who is
playing them. Prisoner's dilemma, and the stag hunt are all symmetric
games.
Asymmetric :
Most commonly studied asymmetric games are games where there
are not identical strategy sets for both players.
Zero-sum games :
In zero-sum games the total benefit to all players in the game, for
every combination of strategies, always adds to zero (more informally,
a player benefits only at the equal expense of others).
Non Zero-sum games :
These type of games have outcomes whose net results are greater or less
than zero
13

14. Simultaneous games :
Are games where both players move simultaneously, or if they do not
move simultaneously, the later players are unaware of the earlier
players' actions (making them effectively simultaneous).
Sequential games (or dynamic games) :
They are games where later players have some knowledge about
earlier actions. This need not be perfect information about every
action of earlier players; it might be very little knowledge. For
instance, a player may know that an earlier player did not perform
one particular action.
Perfect information and Imperfect information :
A game is one of perfect information if all players know the moves
previously made by all other players. Thus, only sequential games
can be games of perfect information, since in simultaneous games not
every player knows the actions of the others.
Many card games are games of imperfect information, for instance
poker.
14

15.  Combinatorial games :
Games in which the difficulty of finding an optimal strategy stems
from the multiplicity of possible moves are called combinatorial
games. Examples include chess and go. Games that involve imperfect
or incomplete information may also have a strong combinatorial
character. A related field of study, drawing from computational
complexity theory, is game complexity, which is concerned with
estimating the computational difficulty of finding optimal strategies.
 Discrete and continuous games :
Continuous games includes changing strategy set.
Much of game theory is concerned with finite, discrete games, that
have a finite number of players, moves, events, outcomes, etc.
15

16.  Infinitely long games :
Pure mathematicians are not so constrained, and set theorists in
particular study games that last for infinitely many moves, with the
winner (or other payoff) not known until after all those moves are
completed. The focus of attention is usually not so much on what is the
best way to play such a game, but simply on whether one or the other
player has a winning strategy.
 Meta-games :
These are games the play of which is the development of the rules for
another game, the target or subject game. Metagames seek to maximize
the utility value of the rule set developed.
16

17. Lesson 1
 Dominance Principle :
Do Not Play A Strictly Dominated Strategy.
Player 2
α β
α
0,0 3,-1
Player 1
β
-1,3 1,1
We say that my strategy α strictly dominates my strategy β if my
payoff from α is strictly greater than that from β regardless of what
others do.
Here playing strategy β is a strictly dominated strategy. 17

18. GAME 1
Put in the box below either the letter α (alpha) or β (beta) .Think of this as a
great bid. I will randomly pair your form with another form and neither your
pair or you would know with whom you were paired.
Here is how grades maybe assigned :-
you pair
α, β – A,C
α, α – B minus , B minus
β, α – C , A
β, β –B plus , B plus
18

19. α, β – A, C
α, α – B minus , B minus
β, α – C , A
β, β –B plus , B plus
MY PAIR ME
(X`) (X)
α β α β
MY
ME
α B A PAIR α C
(X) minus
B
(X`) minus
β C B
plus β A B plus
19

20. MY PAIR
(X`)
α β
Me
(X) α B minus , A,
B minus C
β C, B plus ,
A B plus
Outcome matrix
We cared about our own grade
1)
2) We cared about other grades } 2 Different payoffs
20

21. MY PAIR
(X`)
α β If the pair chooses
alpha and I choose
alpha then I get
zero and if player
ME chooses alpha and I
(X) α 0,0 3, -1 choose beta I get -1.
0 > -1
β -1, 3 1,1
If the player
chooses beta and I
We try to put numbers into perspective and these are called choose alpha I get 3
and if player
# utilities
chooses beta and I
just represent that we optimise our own gain and others loss. choose beta I get 1
(A,C) – 3
3>1
(B minus , B minus )- 0
Hence in both
cases she receives a
higher payoff if she
chooses alpha.

22. MY PAIR
(X`)
α β
ME
(X) α 0,0 -1, -3
β -3,-1 1,1
Replacing (A,C) = -1,(C,A) = -3
22

23. Penalty kick game
Goal keeper
l r
Shooter
L 4,-4 9,-9
M 6,-6 6,-6
R 9,-9 4,-4
23

24. FINALS OF UEFA 2008
MAN Vs CHELSEA
It seemed that Chelsea’s strategy of
going to Van der Sar’s left had been
hatched by someone on the Utd
bench. As Anelka prepared to take
Chelsea’s 7th penalty Van der Sar
pointed to the left corner. Now
Anelka had a terrible dilemma. This
was game theory in its rawest form.
So Anelka knew that Van der Sar
knew that Anelka knew that Van der
Sar tended to dive right against right
footers. Instead Anelka kicked right
but it was at mid-height which
Ignacio warned against.
24

25. Lesson 2
 Put yourself in others shoes and try to
figure out what they will do.
Destroyer
Easy Hard
Easy 1,1 1,1
Savior
Hard 0,2 2,0
 Here savior should look upon the destroyers payoff before
making a move.
25

26. Prisoners Dilemma
 Two Prisoners are on trial for a crime and
each one faces a choice of confessing to the
crime or remaining silent.
The payoffs are given below:
Prisoner 2
Confess Silent
Confess 4,4 1,5
Prisoner 1
Silent 5,1 2,2
26

27. Solution to Prisoners Dilemma
Prisoner 2
Confess Silent
Confess 4,4 1,5
Prisoner 1
Silent 5,1 2,2
 The only stable solution in this game is that
both prisoners confess; in each of the other 3
cases, at least one of the players can switch
from ―silent‖ to ―confess‖ and improve his
payoff.
27

28. Odds to Prisoners Dilemma
 What would the Prisoner 1 and Prisoner 2 decide if
they could negotiate?
 They could both become better off if they reached the
cooperative solution….
which is why police interrogate suspects in separate
rooms.
 Equilibrium need not be efficient. Non-cooperative
equilibrium in the Prisoner’s dilemma results in a
solution that is not the best possible outcome for the
parties.
 Alternative: Implied contract
if there were a long relationship between the parties—
(partners in crime) are more likely to back each other
28

29. CPU Competition
 Intel and AMD compete fiercely to develop innovations
in CPUs for PCs
 As a result of this, CPU speeds have increased
dramatically, but there are few differences between the
products of the two companies
 Even though both companies expended huge amounts
of money to gain a competitive advantage, their relative
competitive position ends up unchanged.
 Both companies are worse off than if they had each
slackened the pace of innovation
 This is an example of a prisoner’s dilemma
29

30. Sale Price Guarantees
 Globus and many other stores like
Pantaloons offer sale price guarantees
◦ If an item comes on sale in the time period
after you bought it, they will match the
difference in prices
◦ Thus, consumers wishing to buy now are
―protected‖ against regrets from future price
reductions
30

31. Walking Down the Demand Curve
 Globus would like to sell goods at high prices
to those with high willingness to pay for them
and then lower prices to capture those with
lower willingness to pay.
 They might do this by running sales after new
items have been out for a while
 But high value consumers will anticipate this
and wait for the sale to occur.
31

32. The Power of Commitment
 By offering to rebate back the difference
in prices, Globus makes the sale strategy
less profitable for its ―future‖ self.
 This commits it to less discounting in the
future
 In fact It enables it to charge higher prices
today…and tomorrow.
32

33. Coordination Game
 Coordination game involves multiple outcomes that can be stable. A simple
Coordination game involves two players choosing between two options,
wanting to choose the same.
 Battle of the Sexes :
33

34. Solution to Battle Of the Sexes
 Solution: Both should play the same game.
 Everyone benefits from being in
cooperative group, but each can do better
by exploiting cooperative efforts of
others.
34

35. Anti Coordination Game
 Routing Congestion Game :
 Solution: The players must coordinate to send
traffic on different connection points.
35

36. Rules of the Game
 The strategic environment
◦ Players – I , j
◦ Strategies- S(i) – strategy of player I
◦ S(i) – set of possible strategies of player
I
◦ S – strategy profile
◦ Payoffs- µ (i)
◦ µi (s) – profile utilities
36

37.  The rules
◦ Timing of moves
◦ Nature of conflict and interaction
◦ Informational conditions
◦ Enforceability of agreements or
contracts
 The assumptions
◦ Rationality
◦ Common knowledge
37

38. Prisoner's Dilemma (communication is not legal)
communication wont help
38

39. Investor game
(where both can communicate legally.)
A communication can help
L R
U 1,1 0,0
D 0,0 1,1
39

40. So far we have used the dominant strategy solution and iterative
elimination of dominated strategy (IEDS) solution concepts to solve
strategic form games. A third approach is to use the Nash equilibrium
concept.
40

41. Nash Equilibrium- Necessary requirements
for a Nash equilibrium are that each player
play a best response against a conjecture,
and the conjecture must be correct.
41

42. Going to movies
He
Person 1 Person 2 Person 3
She
Movie1 2,1 0,0 0,-1
Movie 2 0,0 1,2 0,-1
Movie 3 -1,0 -1,0 -2,-2
Either both people go for movie 1 or
Both go for Movie 2
You call this each persons ―equilibrium‖ or ―Nash equilibrium ―
42

43. How do we identify the Nash equilibria in a game?
Look for the dominant strategy.
Eliminate the dominated strategies.
Play a minimax strategy. In a zero sum game you choose that strategy in
which your opponent can do you the least harm from among all of the
'bad' outcomes.
Cell-by-cell inspection or trial and error
43

44.  1- no regrets as we choosing the best
move
2- Self fulfilling believes
44

45. Coordination game –
1) Your farewell party
2) LED technology
3) Tv shows
4) Software platforms coordination
45

46.  selfish routing in large networks like the Internet
 theoretical basis to the field of multi-agent systems.
 Use of NLP for optimizing results.
46

47. Diverse applications
1)Economics and business
2) Political science
-game-theoretic models in which the players are often voters, states, special
interest groups, and politicians.
3) Biology
-Evolutionary game theory (EGT) is the application of game theory to
evolving populations of lifeforms in biology.
4) Computer science and logic
-Algorithmic game theory and within it algorithmic mechanism design
combine computational algorithm design and analysis of complex systems
with economic theory.
5) Philosophy-common beliefs or knowledge
6) Legal problems and behavioral economics.
47