Total Surface Area of Prisms
- 2. Image Source: http://www.ppfl.org Total Surface Area is important for Painters, so that they know how much paint will be required for a job. Engineers, Designers, Scientists, Builders, Concreters, Carpet Layers, and others also use Total Surface Areas as part of their work.
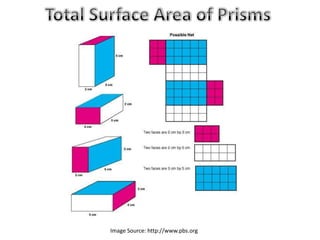
- 3. A 3D Rectangular Prism can be unfolded to create a flat 2D shape, called the “Net” of the Prism.
- 4. The “Total Surface Area” or “TSA” of the Prism is the Area of all of the six faces added together. Each of the Faces is a L x W Rectangle. 8 cm 4 cm
- 5. The “Total Surface Area” = 2 x ( 8 x 5) : Two Blues + 2 x ( 8 x 4) : Two Yellows + 2 x ( 4 x 5) : Two Reds = 2x40 + 2x32 + 2x20 = 184 cm2 8 cm 4 cm 8 x 5 8 x 5 4 x 5 4 x 5 8 x 4 8 x 4
- 6. The “Total Surface Area” = 2 x ( L x W ) : Two Blues + 2 x ( L x H ) : Two Yellows + 2 x ( W x H ) : Two Reds L H L x W L x W W x H W x H L x H L x H TSA = 2 x(L x W) + 2x(L x H) + 2x(W x H)
- 7. TSA = 2 x ( x ) + 2 x ( x ) + 2 x ( x ) TSA = + + TSA = TSA = 2 x(L x W) + 2x(L x H) + 2x(W x H) 6 m 3 m We can do the TSA of a Rectangular Prism without drawing out the flat 2D net. All we do is apply the Formula.
- 8. TSA = 2 x ( 6 x 4 ) + 2 x ( 6 x 3 ) + 2 x ( 4 x 3 ) TSA = 48 + 36 + 24 TSA = 108 m2 ( Note that units are AREA m2 and Not VOLUME m3 ) 6 m 3 m TSA = 2 x(L x W) + 2x(L x H) + 2x(W x H) We can do the TSA of a Rectangular Prism without drawing out the flat 2D net. All we do is apply the Formula.
- 9. The Toblerone chocolate bar packaging is a classic example of a Triangular Prism. Image Source: http://www.blogspot.com
- 10. A 3D Triangular Prism can be unfolded to create a flat 2D shape, called the “Net” of the Prism. The Net has two triangles plus three rectangles.
- 11. The “Total Surface Area” = 2 x ( 6 x 5) /2 : Two Reds + 2 x ( 8 x 7) : Two Yellows + 1 x ( 8 x 6) : One Green = 2x15 + 2x56 + 1x48 = 190 mm2 6 mm 5 mm 8 x 7 ( 6 x 5) /2 8 x 6 8 x 7 ( 6 x 5) /2
- 12. The “Total Surface Area” = 2 x ( b x h) /2 : Two Reds + 2 x ( D x n) : Two Yellows + 1 x ( D x b) : One Green Base b Height h D x n ( b x h) /2 D x b D x n ( b x h) /2TSA = 2 x (b x h)/2 + 2 x (D x n) + (D x b) Only Works for Isosceles Triangle Ended Prisms Only Works for Isosceles Triangle Ends
- 13. For Triangular Prisms, the best general approach is to draw a “Net” of the Prism. From the Net we can work out the Area of the Triangular Ends, and the three rectangles, and then add them all up. We could work out that the above Prism’s Formula as : TSA = 2 x (b x h )/2 + (D x b) + (D x m) + (D x n) But it is probably easier to use a Net and the General Formula: TSA = 2 x Triangle End + Bottom Rectangle + Left Rectangle + Right Rectangle.
- 14. If we only have the edge measurements, then we need to cut the end Triangle in half, and apply Pythagoras Theorem to work out the Missing Height of the Prism. 4 cm ? cm ? cm 8 cm
- 15. A 3D Cylinder can be unwrapped to create a flat 2D shape, called the “Net” of the Cylinder. The Net has two Circles plus one Rectangle.
- 16. W = 10 mH = 10 m TSA = 2 x Circles + Rectangle TSA = TSA = m2 R = 2 L =
- 17. TSA = 2 x Circles + Rectangle TSA = 2 x ∏ x 2 x 2 + 2x ∏ x 2 x 10 TSA = 151 m2 W = 10 2∏R L = 2∏ x 2 Rectangle = L x W Rectangle = 2x ∏ x 2 x 10 Circle = ∏ x 2 x 2 H = 10 m R = 2
- 18. TSA = 2 x Circles + Rectangle TSA = 2 x ∏ x R x R + 2x ∏ x R x H H L = 2∏R Rectangle = L x W Rectangle = 2x ∏ x R x H Circle = ∏ x R x R H TSA = 2∏R2 + 2 ∏RH R
- 19. TSA = 2 x ∏ x R x R + 2 x ∏ x R x H TSA = 2 x 3.1416 x 3 x 3 + 2 x 3.1416 x 3 x 8 TSA = 207.3 m2 H = 8 m TSA = 2∏R2 + 2 ∏RH R = 3 m We can do the TSA of a Cylinder without having to draw out the flat 2D net. All we do is apply the TSA Formula.
- 20. A 3D Square Pyramid can be unwrapped to create a flat 2D shape, called the “Net” of the Pyramid. The Net has one Square and Four Triangles.
- 21. The “Total Surface Area” = 4 x ( 8 x 10) /2 : Four Green Triangles + 1 x ( 8 x 8) : One Blue Purple Square = 4x40 + 1x64 = 224 m2 8 x 8
- 22. http://passyworldofmathematics.com/ All slides are exclusive Copyright of Passy’s World of Mathematics Visit our site for Free Mathematics PowerPoints
