The document provides an overview of cryptographic algorithms, specifically focusing on DES (Data Encryption Standard) for symmetric key cryptography and RSA (Rivest-Shamir-Adleman) for asymmetric key cryptography. It discusses the necessity of secure communication in light of increasing cyber crime in India, explores various cryptographic techniques, and outlines the strengths and weaknesses of each cryptography type. The document concludes with real-life applications and the importance of cryptography in ensuring secure data transactions.

1. Cryptographic
Algorithms:
DES & RSA
Presented By:
Aritra Ranjan Das (13000112077)
Arnab Bhattacharjee (13000112078)
Ipshita Das (13000112103)
Arpan Mondal (13000112081)

2. Overview
Needs for Security
Types of Attack
What is Cryptography?
Basic Terms
Techniques for Cryptography
Types of Cryptography
DES Algorithm for Symmetric key Cryptography
Problems with Symmetric Key Cryptography
RSA Algorithm for Asymmetric Key Cryptography
Real Life Applications of Cryptography
Conclusion
References

3. Needs for Security in India
• Computer Applications has been
developed to handle financial and
personal data.
• India has bypassed Japan to become
the world’s third largest Internet user
after China and the United States.
• This encourages a group of people to
indulge in cyber crime activities.
• India ranked 11th in the cyber crime
activities in the world [1].
Alice (Sender)
Bob (Receiver)
Medium
Eve
(Unauthorized
Person)

4. Needs for Security in India
Figure: Number of cyber crime complaints registered in India [2]

5. Types of Attack
ATTACKS
INTERCEPTION FABRICATION MODIFICATION INTERRUPTION
Passive Attacks Active Attacks

6. CRYPTOGRAPHY
What is Cryptography?
• Cryptography came from Greek kryptós, "hidden", + gráphein, "to
write".
• Cryptography is the art of achieving security by encoding messages to
messages to make them non-readable.
• It provides Confidentiality, Integrity, Accuracy.
CRYPTOGRAPHY

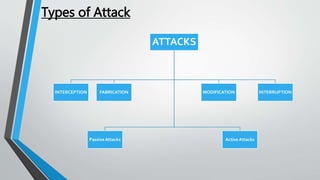
7. Basic Terms
• Plain Text: Message before encryption.
• Cipher Text: Message after encryption.
• Cipher: Encryption algorithm
• Encryption: the process of converting Plain text to Ciphertext
• Decryption: the process of converting ciphertext back to the original plaintext.
• Key: Sequence that controls the operation and behavior of the cryptographic
algorithm.
Figure: General working principle of Cryptography [3]

8. Techniques for Cryptography
1. Substitution Technique: In substitution cipher technique, the
characters of a plain text message are replaced by other Characters,
Characters, Number or Symbols.
Example: Caesar Cipher.
• Caesar Cipher is a special case of substitution technique wherein each message
message is replaced by an alphabet three place down the line.
• To decrypt Caesar Cipher we have to replace each alphabet in cipher text
text message with the alphabet that is three place up the line.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
F R P H K H U H
C O M E H E R E

9. Techniques for Cryptography (Contd..)
2. Transposition Technique: Transposition techniques differ from
substitution techniques in the way that they do not simply replace
replace one alphabet with another; they also perform some
permutation over the plain text alphabets.
Example: Rail Fence Technique
• Write down the plain text message as a sequence of diagonals.
• Read the plain text written in step 1 as a sequence of rows.
Original plain text message: Come home tomorrow
C m h m t m r o
o e o e o o r w
CipherText: cmhmtmrooeoeoorw

10. Types of Cryptography
1. Symmetric Key Cryptography:
• Symmetric key cryptography involves the usage of the same key for encryption
encryption and decryption [4].
• Both sender and receiver must know the common key.
• The common key need to be exchanged before hand by some other secure
secure method.
Figure: Working principle of Symmetric Key Cryptography [5]

11. Data Encryption Standard(DES)
• Symmetric Key Algorithm
• Derived from IBM’s Lucifer
• Approved as a standard in 1977 by the U.S Government

12. 64-bit
Plain Text
DES
64-bit
Cipher Text
64-bit
Plain Text
64-bit
Plain Text
DES DES
64-bit
Cipher Text
64-bit
Cipher Text
56-bit key 56-bit key 56-bit key…
Block 1 Block 2 Block n
The 56-bit key is derived from a 64-bit key by eliminating
all 8 bit positions.
In other words bits positions 8,16,24,32,40,48,56 and 64
are discarded.
Key Derivation:
…

13. Initial Permutation : Before the plain text is
encrypted with the key the bit positions of the plain
plain text are transposed .
Bit position in plain text block Overwritten by contents of bit
position
1 58
2 50
3 42
… …
64 7
The permuted block is divided into two blocks, namely
Left Plain Text (LPT) and Right Plain Text (RPT).
Original Plain Text of 64 bits
Left Plain Text (LPT) of 32 bits Right Plain Text (RPT) of 32 bits

14. Key Transformation:
• The 56-bit key is divided into two 28-bit segments. Each segment
undergoes a circular left shift of 1 or 2 bits depending on the round of
encryption (16 total rounds).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
Round
Number of
bits shifted
• After appropriate bit shifting 48 of the 56 bits are selected to form the
final encryption key. This is known as compression permutation.
14 17 11 24 1 5 3 28 15 6 21 10
23 19 12 4 26 8 16 7 27 20 13 2
41 52 31 37 47 55 30 40 51 45 33 48
44 49 39 56 34 53 46 42 50 36 29 32

15. Expansion Permutation:
Right Plain Text (RPT) of 32 bits from previous step
Block 1 (4 bits) Block 2 (4 bits) Block 8 (4 bits)
Input Block 1 (4 bits)
1 2 3 4
Input Block 2 (4 bits)
5 6 7 8
Input Block 8 (4 bits)
29 30 31 32
1 2 3 4 5 6
Output Block 1 (6 bits)
7 8 9 10 11 12
Output Block 2 (6 bits)
43 44 45 46 47 48
Output Block 8 (6 bits)
48-bit Key 48-bit RPTXOR
S-box Substitution

16. S-box Substitution:
In S-box substitution the 48-bit encrypted text is broken into 6-bit
blocks and each block is used to generate a 4-bit output block by
using an S-box
48-bit input block
6-bit sub block 6-bit sub block 6-bit sub block
S-box 1 S-box 8S-box 2
4-bit output 4-bit output4-bit output
…
32-bit output block
From each 6-bit block the MSB and LSB combine together to select the row
number and the intermediate bits select the column number in the 4x16 S-
box which contains a corresponding 4-bit number.
…

17. 1.Key Transformation
2.Expansion Permutation
3.S-box Substitution
4.P-box Permutation
P-Box Permutation: The output of S-box consists of 32 bits. These bits
are permuted using P-box with a straight forward permutation
mechanism.
XOR & Swap:
Original 64-bit Plain Text Block
32-bit Left Plain Text (LPT) 32-bit Right Plain Text (RPT)
32-bit Left Plain Text (LPT) 32-bit Right Plain Text (RPT)
XOR
Next Round
Final Permutation: At the end of 16 rounds, the Final Permutation is performed
(only once) which is a simple transposition.

18. Strength Of DES Algorithm:
• The Strength of DES Algorithm lies in its key, which must be
secret.
• DES uses 64-bits key.
• Thus, there are 264 possible keys
• Hence, Brute-Force attack on DES is impractical
• It would require more than 1,000 years to break DES.

19. Problems with Symmetric Key Cryptography:
• Problem of Key Distribution
• Large number of keys required (One for each pair of
communicating parties)
For n persons, the number of lock-and-key pairs are :
n*(n-1)/2!
Hence, for 1000 persons we will have 499,500 lock-and-key
pairs!!!
• A trusted party is required to manage all the keys
Parties Involved Lock-and-Key pairs Number of lock-key pair
2 (A,B) (A-B) 1
3 (A,B,C) (A-B,A-C, B-C) 3
4 (A,B,C,D) (A-B,A-C, A-D, B-C, B-D, C-D) 6

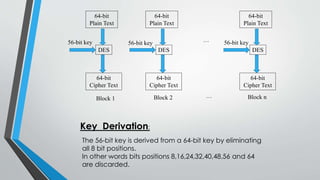
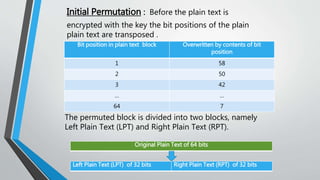
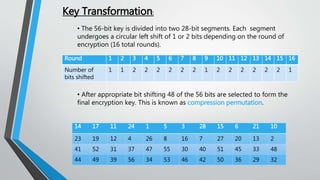
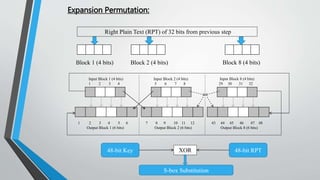
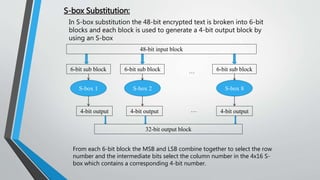
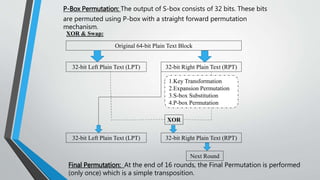
20. Types of Cryptography (Contd…)
2. Asymmetric Key Cryptography:
• Two different keys are used to encrypt and decrypt the message.
• Receiver generates a public and private key pair.
• Receiver broadcasts the public key.
• Encryption is done by public key and private key is used for decryption.
Figure: Working principle of Asymmetric Key Cryptography [6]

21. RSA Algorithm
• by Rivest , Shamir & Adleman of MIT in 1977
• best known & widely used public-key scheme
• security due to cost of factoring large numbers
RSA Algorithm
• by Rivest , Shamir & Adleman of MIT in 1977
• best known & widely used public-key scheme
• security due to cost of factoring large numbers

22. RSA Key Setup
• each user generates a public/private key pair by:
• selecting two large primes at random : p, q
• computing their system modulus N=p * q
• Note : ø(N)=(p-1)(q-1)
• selecting at random the encryption key : e
• where 1<e<ø(N), gcd(e,ø(N))=1
• solve following equation to find decryption key : d
• d ≡ e−1 (mod φ(n)) and 0≤d≤N
• publish their public encryption key: KU= {e , N}
• keep secret private decryption key: KR={d , p , q}

23. RSA Use
• To encrypt a message M the sender:
• obtains public key of recipient KU={e , N}
• computes: C ≡ Me mod N, where 0≤M<N
• To decrypt the ciphertext C the owner:
• uses their private key KR={d , p, q}
• computes: M ≡ Cd mod N
• Note that the message M must be smaller than the
modulus N (block if needed)

24. EXAMPLE OF RSA ALGORITHM
C
BOB wants to send a message
(M) to ALICE.
*Public Key KU{ e , N} is available
to
sender(BOB)
*Encrypting M, to create the cipher
text(C).
*Sending C to receiver ALICE
*Decrypting Cipher text (C):
Figure: Explanation Of RSA
[7]

25. Setting up RSA Cryptosystem(RECEIVER’S SIDE)
• Algorithm
1. A user must first choose
two large prime numbers, say
p and q
2.Calculate n = p * q
3.Calculate φ(n) = (p-1) * (q-
1)
• Example
1.Let Alice choose.
p=11 and q=19
2.Alice calculated p * q as 11
* 19 and got the value of n =
209.
3.Alice calculated (p-1) * (q-
1) as 10 * 18 and got the
value of φ(n) = 180.

26. Setting up RSA Cryptosystem(RECEIVER’S SIDE)
Algorithm
4.Choose a value of e such that
GCD(e,φ(n)) = 1.
5.Calculate d such that e * d(mod
φ(n))=1 , or in other words, find
the modular multiplicative inverse
of e.
• Applying Euclid's:
180 = 1 * 103 + 77
103 = 1 * 77 + 26
77 = 2 * 26 + 25
26 = 1 * 25 + 1
Example
4.Alice randomly chose e as
103 which is co-prime to 180.
5.To find the required inverse,
Alice would use Euclid's
Algorithm in reverse manner
and then use its extension to
find the inverse. Here's how:
Remember, Alice chose e =
103 and φ(n) = 180

27. Setting up RSA Cryptosystem(RECEIVER’S SIDE)
Algorithm
Reversing Euclid's:
1 = 26 – 25
= 26 – (77 – 2*26)
= 3 * 26 – 77
= 3 * (103 – 77) – 77
= 3 * 103 – 4 * 77
= 3 *(103) – 4 * (180 – 103)
1 = 7 * 103 – 4 * 180
(Bezout's Identity)
Example
Remember, Bezout's Identity is in the
form
ax + by = gcd ( a, b)

28. Setting up RSA Cryptosystem(RECEIVER’S SIDE)
• Finding Inverse:
We now write our Bézout's Identity as ex + φ(n)y = 1, and
we just determined x as 7.
Now, the inverse of e is e-1≡ x (mod φ(n)) ≡ 7 (mod 180)
Hence, d = 7

29. Setting up RSA Cryptosystem(RECEIVER’S SIDE)
Algorithm
6.The Public keys are (e,n),
Example
6.Alice thus obtained her
Public Key as (103,209) and
7.Private Key as (7, 209)

30. Encryption Process(SENDER’S SIDE)
Algorithm
In order to encrypt a
number m, we calculate
c≡me (mod n), where c is the
the encrypted number and
and m is less than n,
keeping in mind that the
encryption (public) key is
(e,n).
Example
Bob wants to send Alice
and important number, say
10. The cipher using Alice's
public key would be
c≡10103 (mod 209)
On calculating this, which
comes out to be 32, Bob
sends it to Alice.

31. Decryption Process(RECEIVER’S SIDE)
Algorithm
In order to decrypt a cipher
cipher c, we calculate m≡cd
Example
Alice receives the
encrypted number. The
decrypted number using
her private key would be
m≡327 (mod 209)
On calculating this, she
gets m=10, which was
desired.

32. ADVANTAGES
1. Convenience
2. Provides for message authentication
3. Detection of tampering
4. Provide for non-repudiation

33. DISADVANTAGES
1. Public keys should/must be authenticated
2. Slow
3. Uses up more computer resources
4. Widespread security compromise is possible
5. Loss of private key may be irreparable

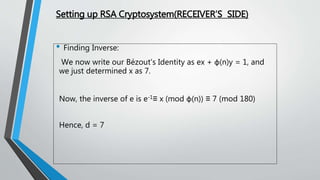
34. Real Life Application Of Cryptography[8]
• Authentication and Digital Signatures
• Time stamping
• Electronic Cash transaction
• Disk encryption

35. Conclusion
• Cryptography is literally everywhere.
• Do not rely on ‘security by obscurity’.
• Cryptographic theory is a very active field of research.

36. References
• [1]: http://www.dnaindia.com/india/report-indore-industries-lose-rs-18k-
cryr-to-cyber-crimes-1930610
• [2]: http://www.medianama.com
• [3]: http://www.slideshare.net/priyavinkal/cryptography-10858819(slide
number: 7)
• [4]: Cryptography and Network Security By Atul Kahate (ISBN: 0-07-
049483-5)
• [5]: http://www.slideshare.net/priyavinkal/cryptography-108588(slide
number: 11)
• [6]: http://www.slideshare.net/priyavinkal/cryptography-108588(slide
number: 14)
• [7]: www.youtube.com
• [8]: www.laits.utexas.edu/../life.html

37. Thank You
Do you have any Questions?