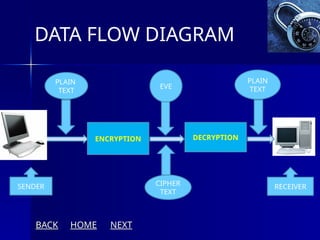
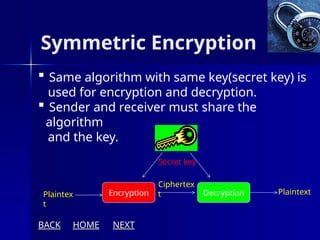
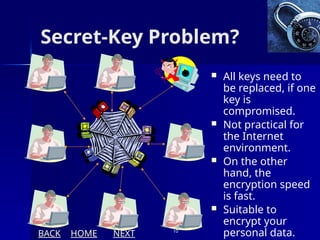
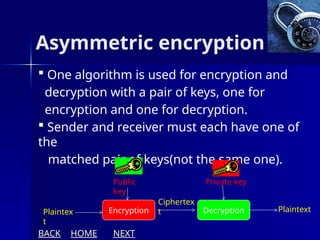
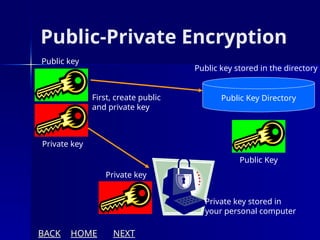
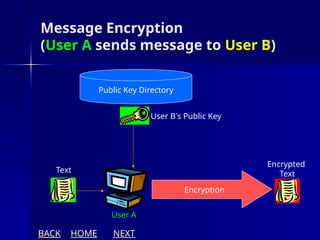
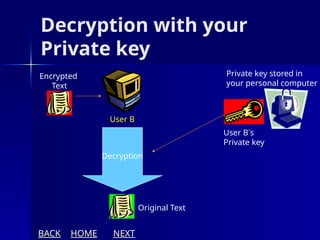
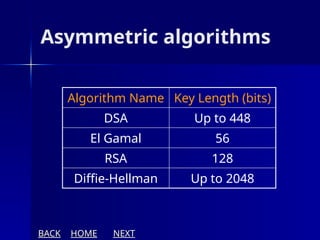
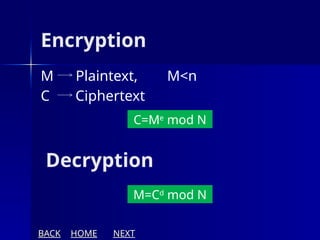
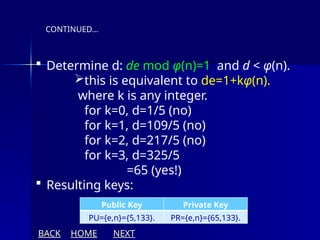
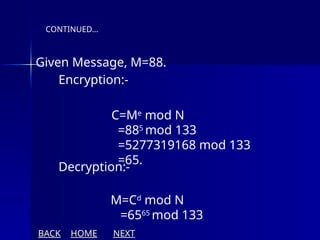
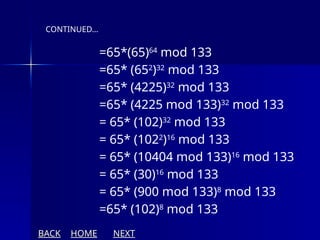
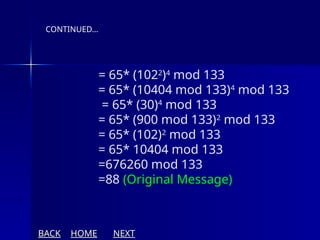
The document presents an overview of cryptography, specifically focusing on encryption and decryption methods, including symmetric (DES) and asymmetric (RSA) algorithms. It explains the fundamental concepts like plaintext, ciphertext, and the role of keys in data security, as well as the advantages and disadvantages of each encryption method. Additionally, it discusses key generation for RSA and its security considerations.

1. ENCRYPTION
AND
DECRYPTION
Presented By:-
Anchal Bhardwaj(0581522008)
And
Ruchi Jain(0161522008)

2. OUTLINE
 Introduction
 Encryption
 Decryption
 Algorithms
 Symmetric Encryption
DES Algorithm
 Asymmetric Encryption
RSA Algorithm
 Comparison
 Summary
BACK NEXT

3. INTRODUCTION
 Cryptography is the science of information
security.
 The word is derived from the Greek kryptos,
meaning hidden.
 Cryptography components:-
Plain Text
Cipher Text
Encryption
Decryption
BACK HOME NEXT

4.  Plaintext : It is original intelligible message ,
before being transformed .The data are not
encrypted.
 Ciphertext : After the message is transformed .
The data are encrypted.
 Alice : Alice is the person who needs to send
secure data.
 Bob : Bob is the recipient of the data.
 Eve : Eve is the person who somehow disturbs
the communication between Alice and Bob.
BACK HOME NEXT

5. ENCRYPTION DECRYPTION
PLAIN
TEXT
CIPHER
TEXT
PLAIN
TEXT
SENDER RECEIVER
EVE
DATA FLOW DIAGRAM
BACK HOME NEXT

6. ENCRYPTION
 It is the process in which plaintext or data is
converted into unintelligible form by means of
a reversible translation, based on a
translation table or algorithm .
BACK HOME NEXT
Encrypted Text
Original Text
+
Key
=
Encryption

7. DECRYPTION
 It is the proces in which encrypted text or
data
(called ciphertext) is translated back into the
original text or data (called plaintext).
Encrypted Text Original Text
Key
+ =
Decryption
BACK HOME NEXT

8. ALGORITHMS
 Symmetric
Encryption(Conventional
Encryption)
 Asymmetric Encryption(Public-key
Encryption)
BACK HOME NEXT

9. Symmetric Encryption
 Same algorithm with same key(secret key) is
used for encryption and decryption.
 Sender and receiver must share the
algorithm
and the key.
Secret key
BACK HOME NEXT
Plaintex
t
Encryption Decryption Plaintext
Ciphertex
t

10. Secret-Key Problem?
 All keys need to
be replaced, if one
key is
compromised.
 Not practical for
the Internet
environment.
 On the other
hand, the
encryption speed
is fast.
 Suitable to
encrypt your
personal data.
10
BACK HOME NEXT

11. Symmetric encryption
algorithms
Algorithm Name Key Length (bits)
Blowfish Up to 448
DES 56
IDEA 128
RC2 Up to 2048
RC4 Up to 2048
RC5 Up to 2048
Triple DES 192
BACK HOME NEXT

12. DES Algorithm
 The data encryption standard (DES) was
developed in the 1970s by the NATIONAL
BUREAU OF STANDARDS (NBS) with the help
of the NATIONAL SECURITY AGENCY (NSA).
Most widely used encryption algorithm until
recently.
 Exhibits the classic Feistel Structure.
 Uses a 64-bit block and a 56-bit key.
BACK HOME NEXT

13. Asymmetric encryption
 One algorithm is used for encryption and
decryption with a pair of keys, one for
encryption and one for decryption.
 Sender and receiver must each have one of
the
matched pair of keys(not the same one).
BACK HOME NEXT
Public
key
Plaintex
t
Encryption Decryption
Ciphertex
t Plaintext
Private key

14. Public-Private Encryption
First, create public
and private key
Public key
Private key
Private key
Private key stored in
your personal computer
Public Key Directory
Public Key
Public key stored in the directory
BACK HOME NEXT

15. Message Encryption
(User A sends message to User B)
Public Key Directory
Text
User A
User B’s Public Key
Encryption
Encrypted
Text
BACK HOME NEXT

16. Decryption with your
Private key
Encrypted
Text
User B’s
Private key
Private key stored in
your personal computer
Decryption
Original Text
User B
BACK HOME NEXT

17. Asymmetric algorithms
Algorithm Name Key Length (bits)
DSA Up to 448
El Gamal 56
RSA 128
Diffie-Hellman Up to 2048
BACK HOME NEXT

18. RSA Algorithm
 Published in the paper A Method for
Obtaining
Digital Signatures and Public-Key
Cryptosystems
in 1977 by Ron Rivest, Adi Shamir and Len
Adleman.
 Most widely accepted and implemented
general-
purpose approach to public-key encryption.
 Block cipher scheme in which the plaintext
BACK HOME NEXT

19. Key Generation
 Choose two distinct prime numbers p and q.
For security purposes, the prime integers
p and q should be chosen uniformly at
random and should be of similar bit-
length.
 Compute n = pq.
n is used as the modulus for both the
public and private keys.
 Compute φ(pq) = (p 1)(
− q 1). (
− φ is Euler's
totient function).
BACK HOME NEXT

20.  Choose a small integer e, such that
 1<e< φ(n).
 e is coprime to φ(n) i.e GCD(e,φ(n)).
 Determine d which satisfies the congruence
relation:-
 de=1(mod φ(n)), Where d< φ(n).
 Publish their public encryption key:
PU={e,n}.
 Keep secret private decryption key:
CONTINUED…
BACK HOME NEXT

21. Encryption
M Plaintext, M<n
C Ciphertext
C=Me
mod N
Decryption
M=Cd
mod N
BACK HOME NEXT

22. RSA Example
 Select primes: p=7 and q=19.
 Compute n = p * q = 7 * 19 = 133.
 Compute ø(n)=(p–1)(q-1)=6×18=108.
 Select e such that GCD(e,108)=1
for e=2, GCD(2,108)=2 (no)
for e=3, GCD(3,108)=3 (no)
for e=4, GCD(4,108)=4 (no)
for e=5, GCD(5,108)=1 (yes!)
Thus, choosing e=5.
BACK HOME NEXT

23. CONTINUED…
 Determine d: de mod φ(n)=1 and d < φ(n).
this is equivalent to de=1+kφ(n).
where k is any integer.
for k=0, d=1/5 (no)
for k=1, d=109/5 (no)
for k=2, d=217/5 (no)
for k=3, d=325/5
=65 (yes!)
 Resulting keys:
Public Key Private Key
PU={e,n}={5,133}. PR={e,n}={65,133}.
BACK HOME NEXT

24. Given Message, M=88.
Encryption:-
Decryption:-
CONTINUED…
C=Me
mod N
=885
mod 133
=5277319168 mod 133
=65.
M=Cd
mod N
=6565
mod 133
BACK HOME NEXT

25. =65*(65)64
mod 133
=65* (652
)32
mod 133
=65* (4225)32
mod 133
=65* (4225 mod 133)32
mod 133
= 65* (102)32
mod 133
= 65* (1022
)16
mod 133
= 65* (10404 mod 133)16
mod 133
= 65* (30)16
mod 133
= 65* (900 mod 133)8
mod 133
=65* (102)8
mod 133
CONTINUED…
BACK HOME NEXT

26. = 65* (1022
)4
mod 133
= 65* (10404 mod 133)4
mod 133
= 65* (30)4
mod 133
= 65* (900 mod 133)2
mod 133
= 65* (102)2
mod 133
= 65* 10404 mod 133
=676260 mod 133
=88 (Original Message)
CONTINUED…
BACK HOME NEXT

27. RSA Security
 Three approaches to attacking RSA:
– brute force key search (infeasible given size
of numbers)
– mathematical attacks (based on difficulty of
computing ø(N), by factoring modulus N)
– timing attacks (on running of decryption)

28. Advantages
 Increased security and convenience.
 Provide digital signatures that cannot be
repudiated.
 Best used in multi-user environment.
Disdvantages
 About 1000 times slower than DES.
 Computational cost is high.

29. SYMMETRIC ENCRYPTION ASYMMETRIC ENCRYPTION
 Same algorithm with the
same key is used for
encryption and decryption.
 One algorithm is used for
encryption and decryption with a
pair of keys, one for encryption
and other for decryption.
 Sender and receiver must share
the algorithm and the key.
 Sender and receiver must each
have one of the matched pair of
keys(not the same one).
 Key must be kept secret.  One of the two keys must be kept
secret.
 Faster as compared to asymmetric
encryption.
 About 1000 times slower than
symmetric encryption.
 Generally more secure and less
computationally less expensive .
 Less secure and computational
cost is relatively high.
 Best used for digital signatures
and
 Best used for Bulk data encryption
.
BACK HOME NEXT
Comparison

30. Summar
y
 Cryptography
 Encryption
 Decryption
 Algorithms
Symmetric encryption
DES
Asymmetric encryption
RSA
 Comparison
BACK HOME NEXT

31. References
“Cryptography and Network Security” by
William
Stallings.
“Computer Networks” by Andrew S.
Tanenbaum.
 Google.com.
 Wikipedia.com
BACK HOME NEXT

32. END SHOW