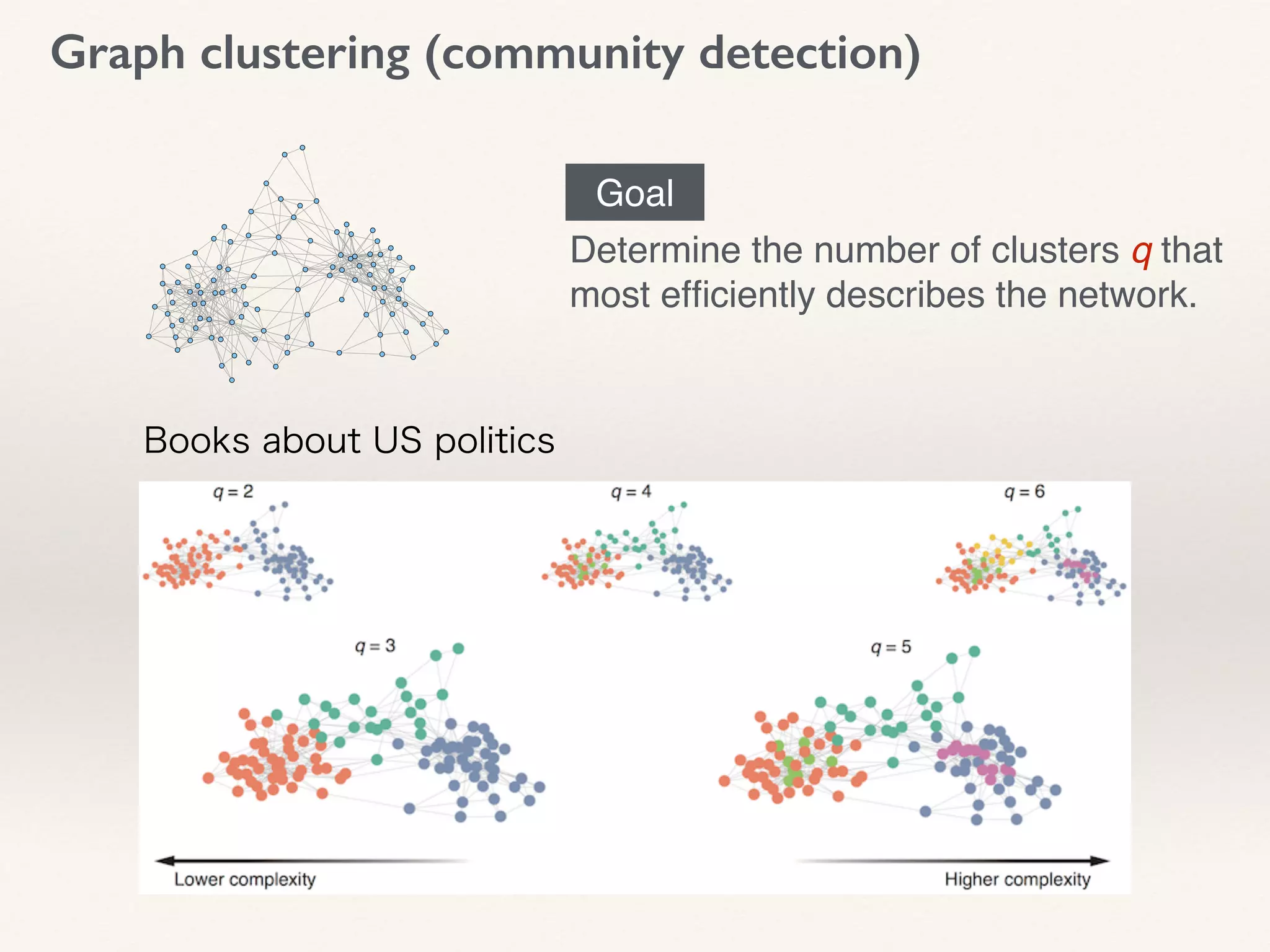
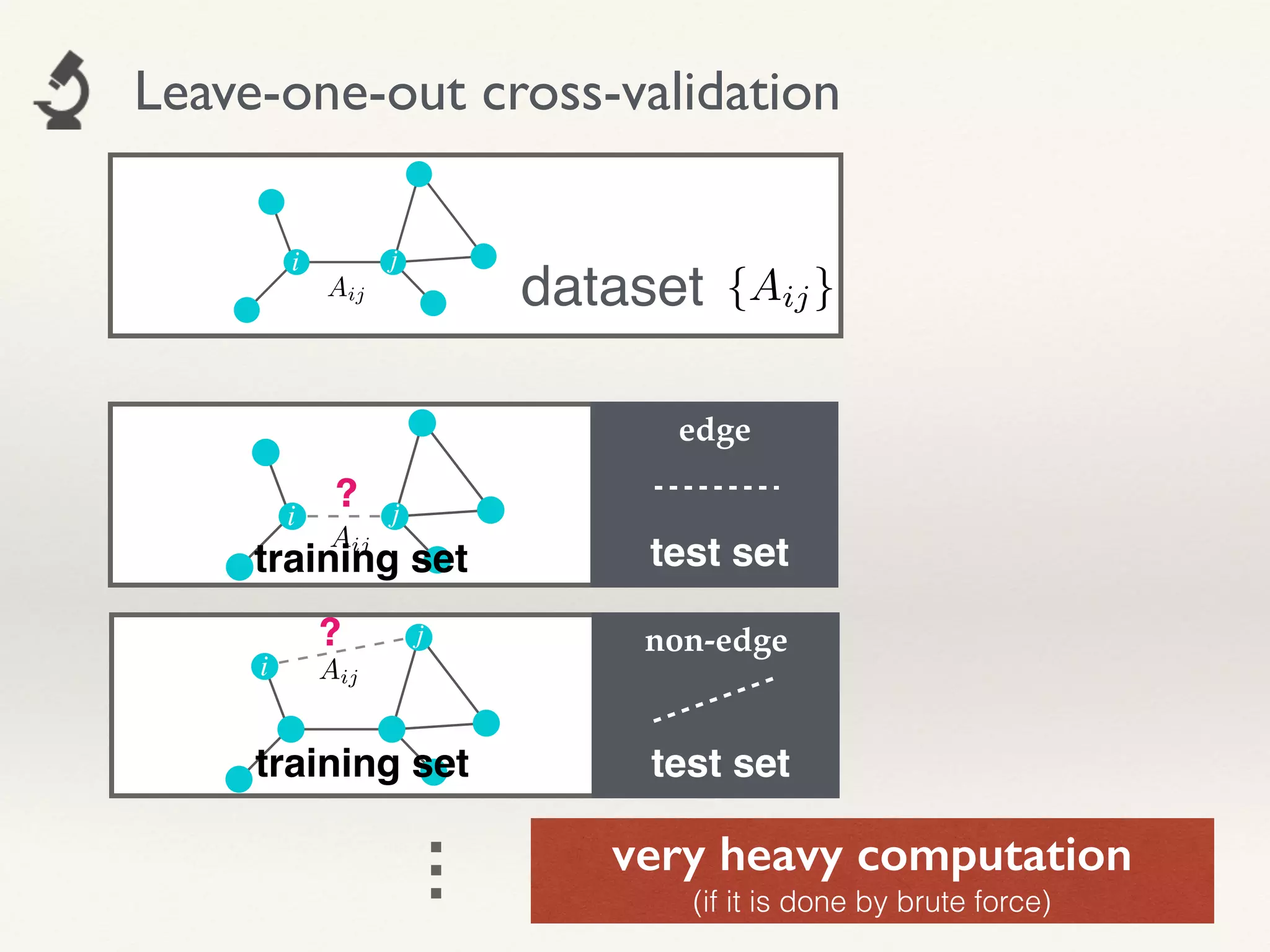
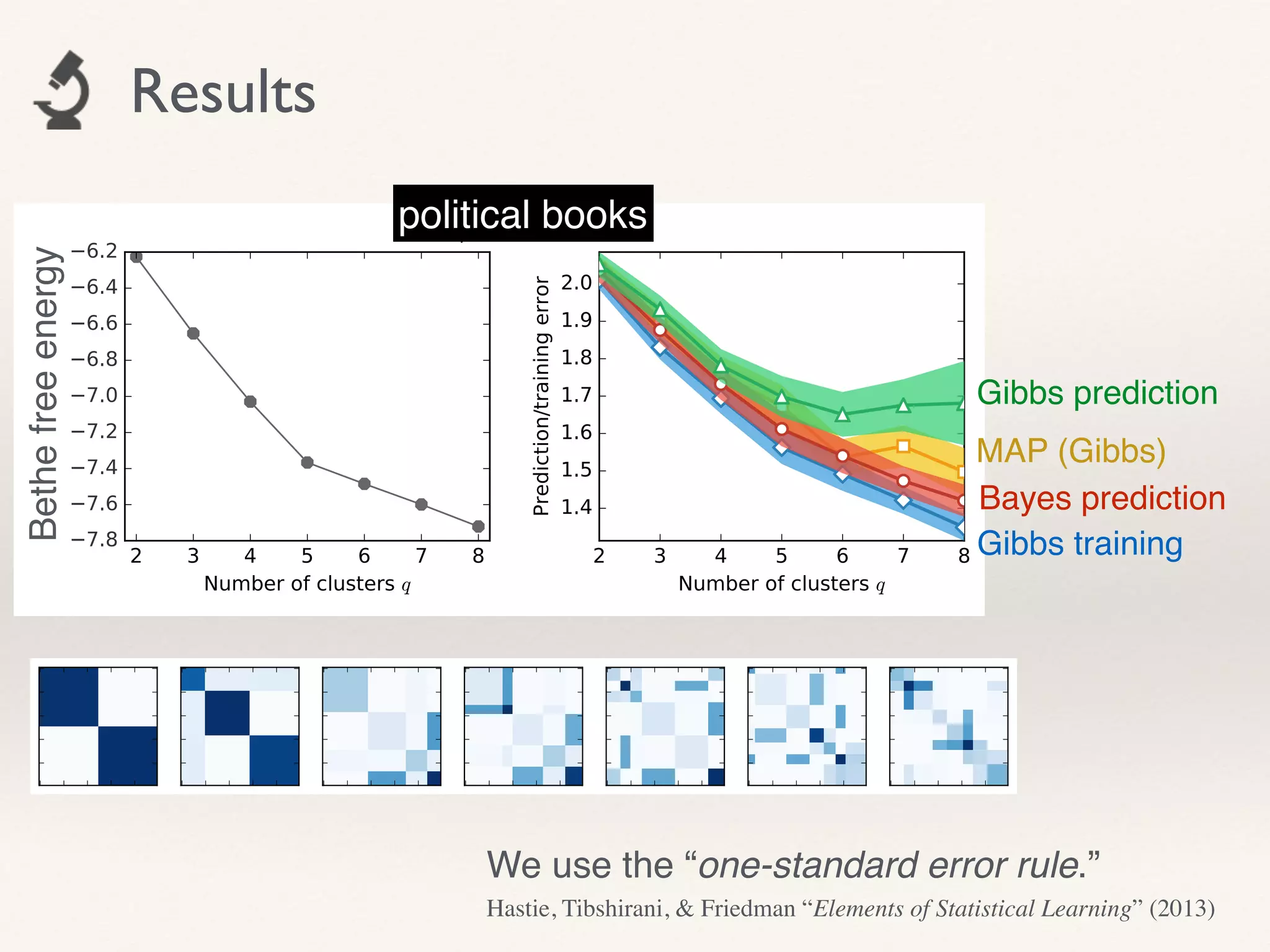
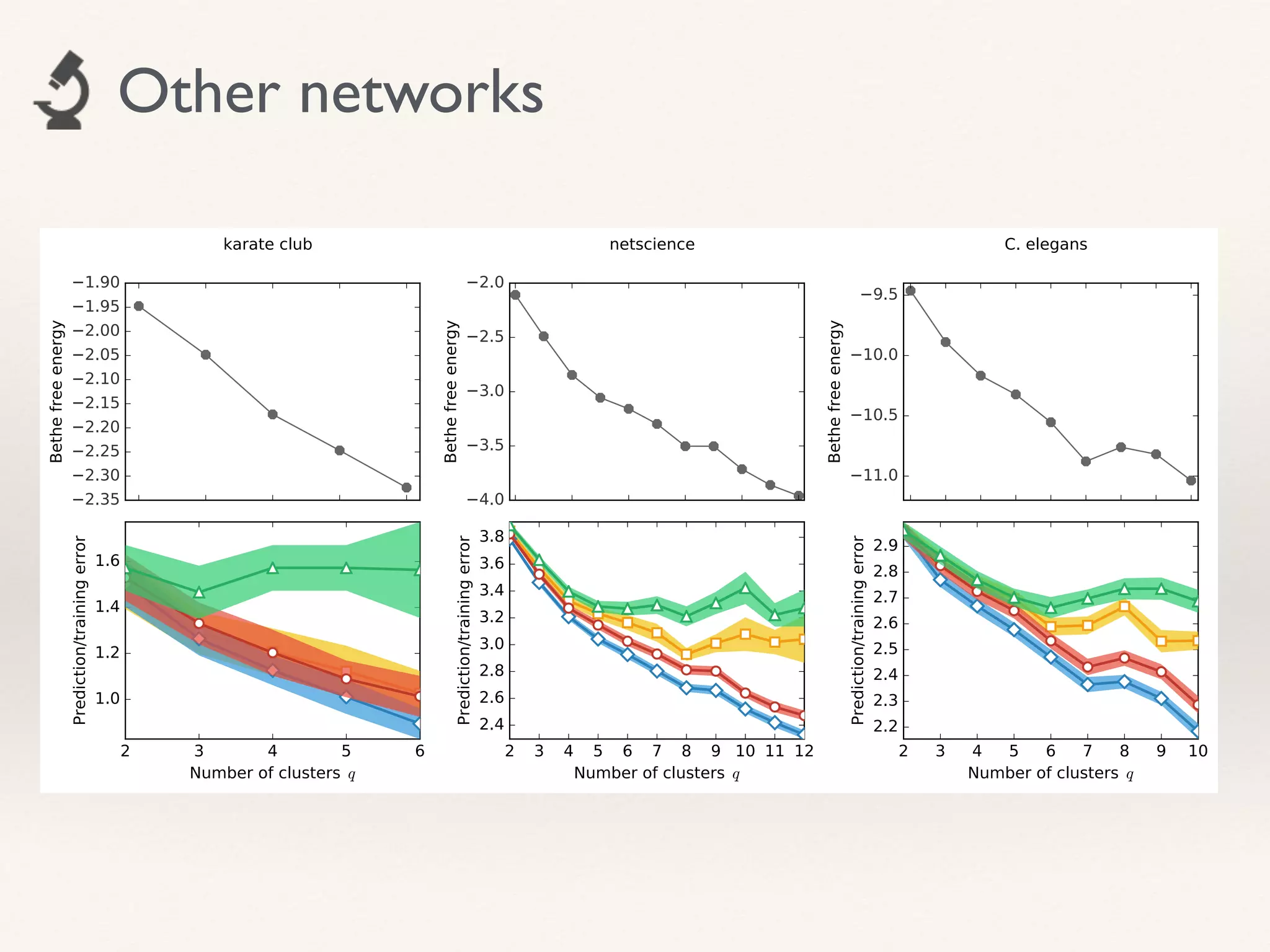
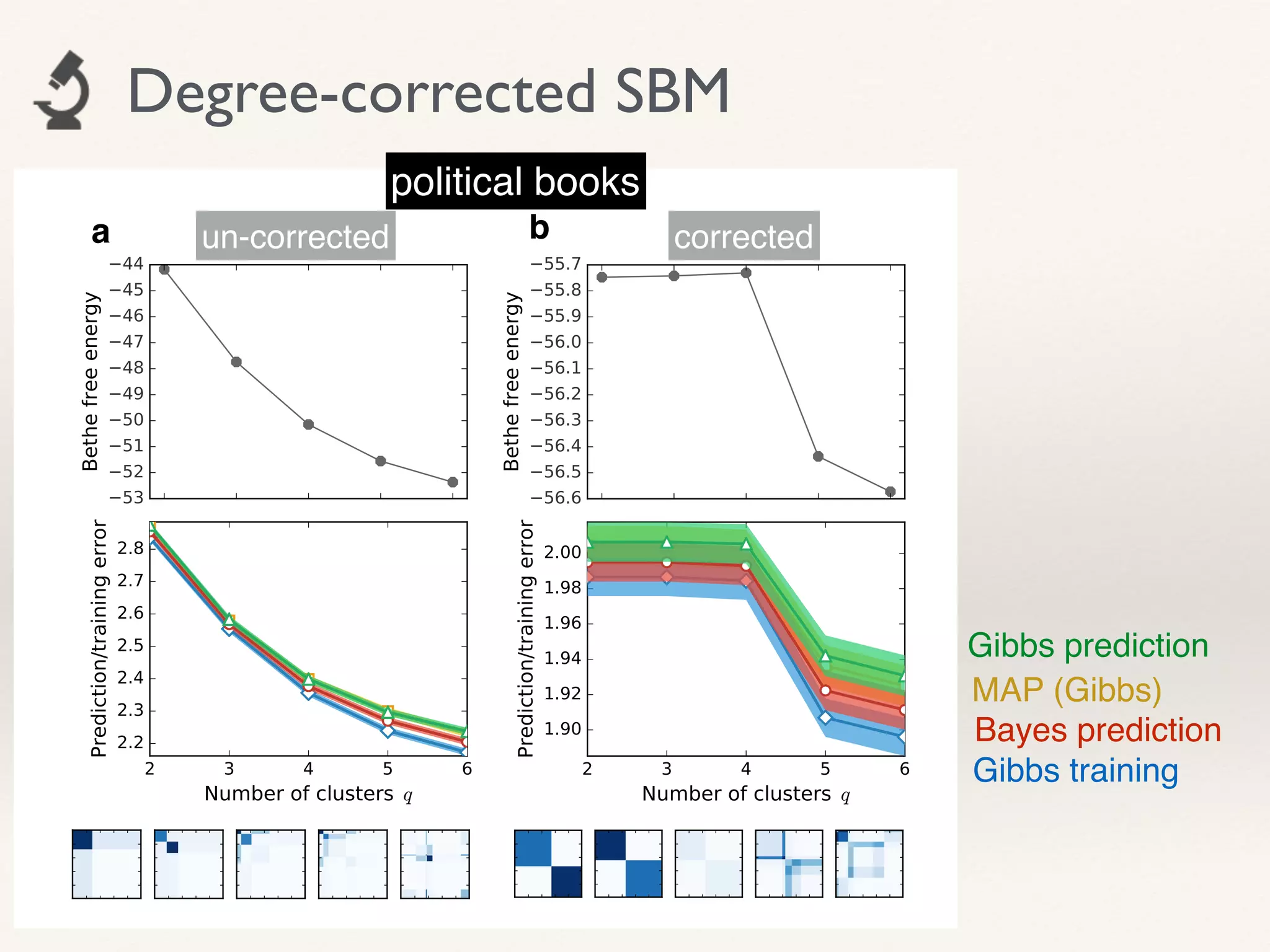
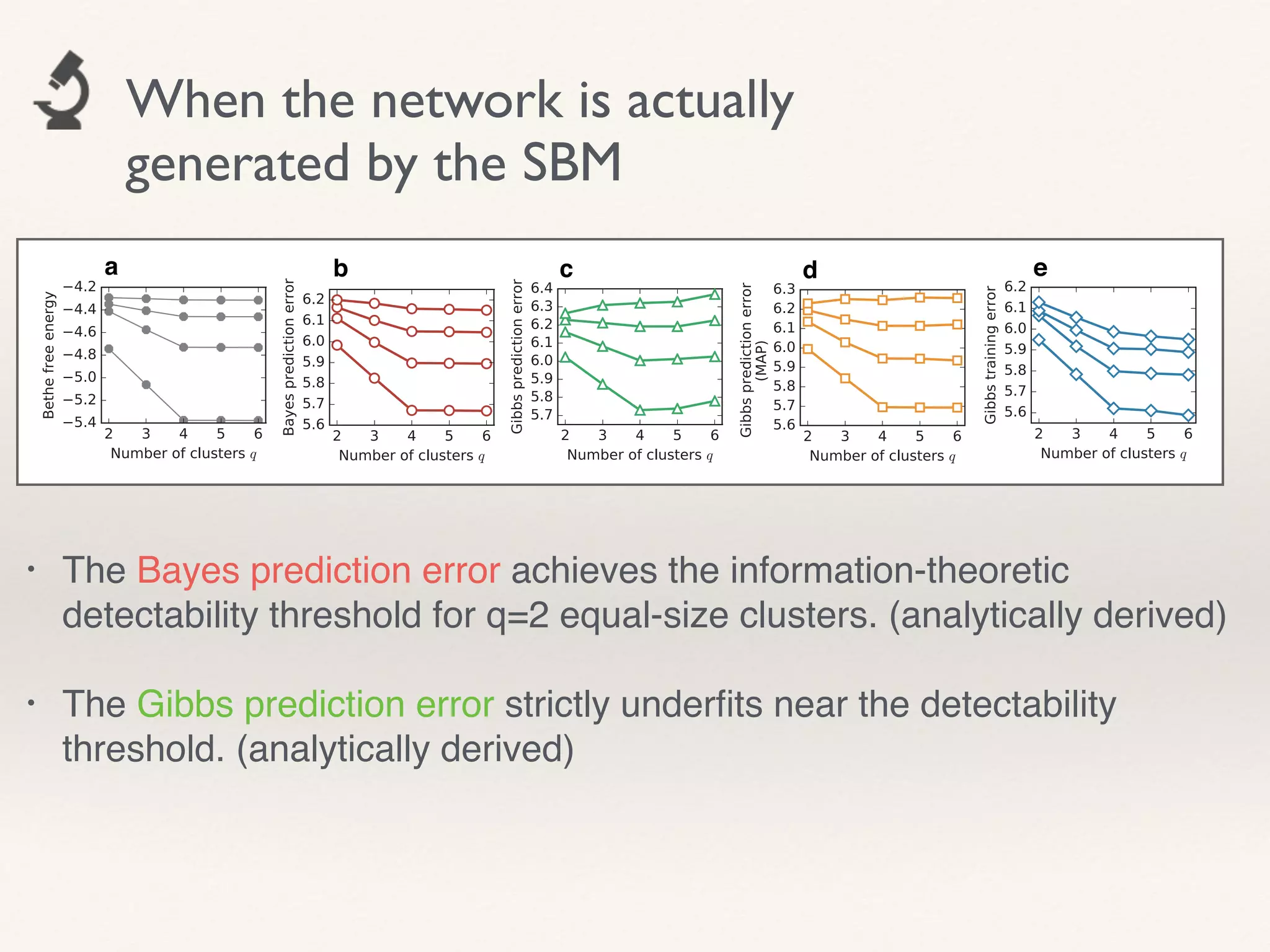
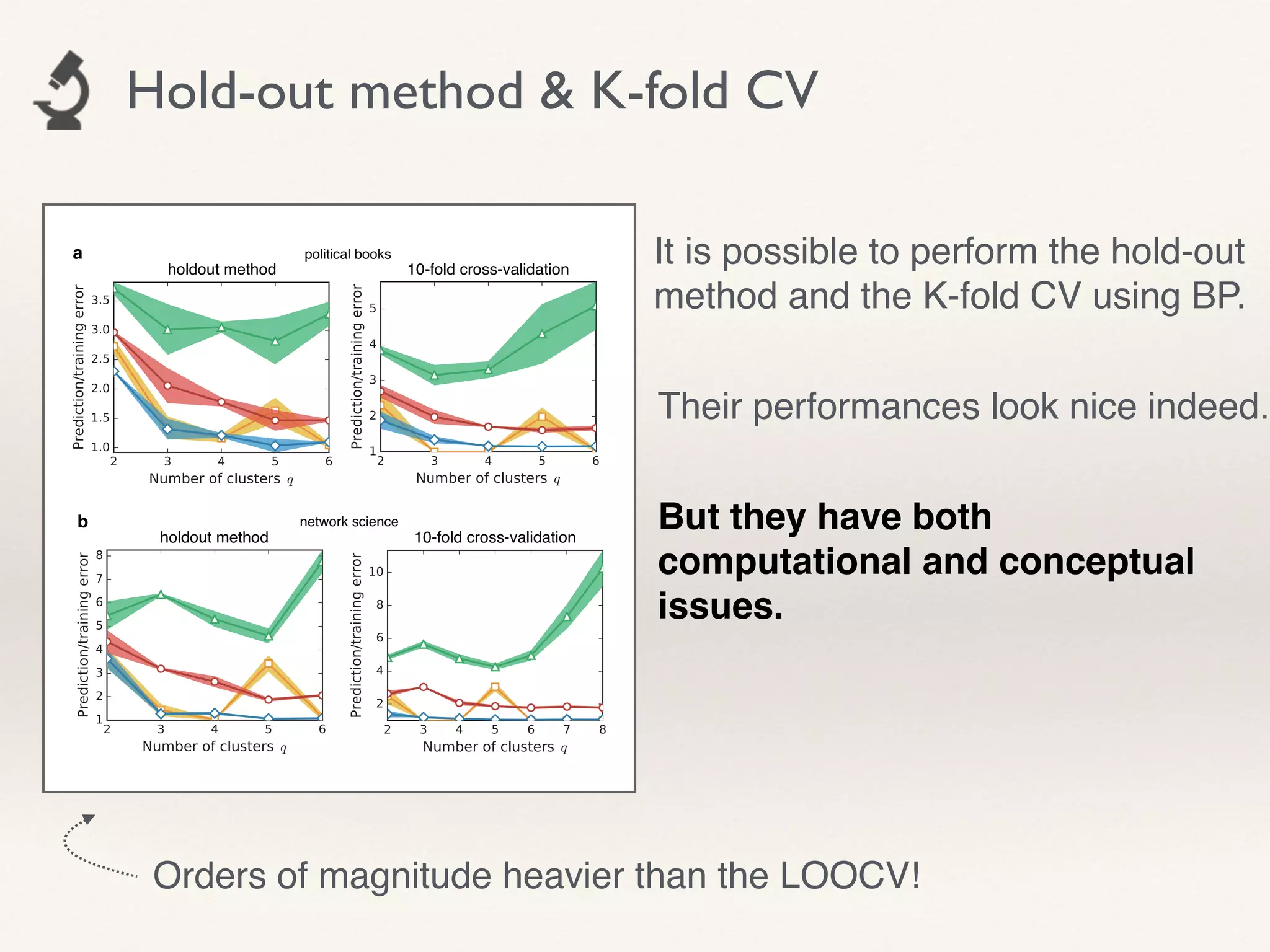
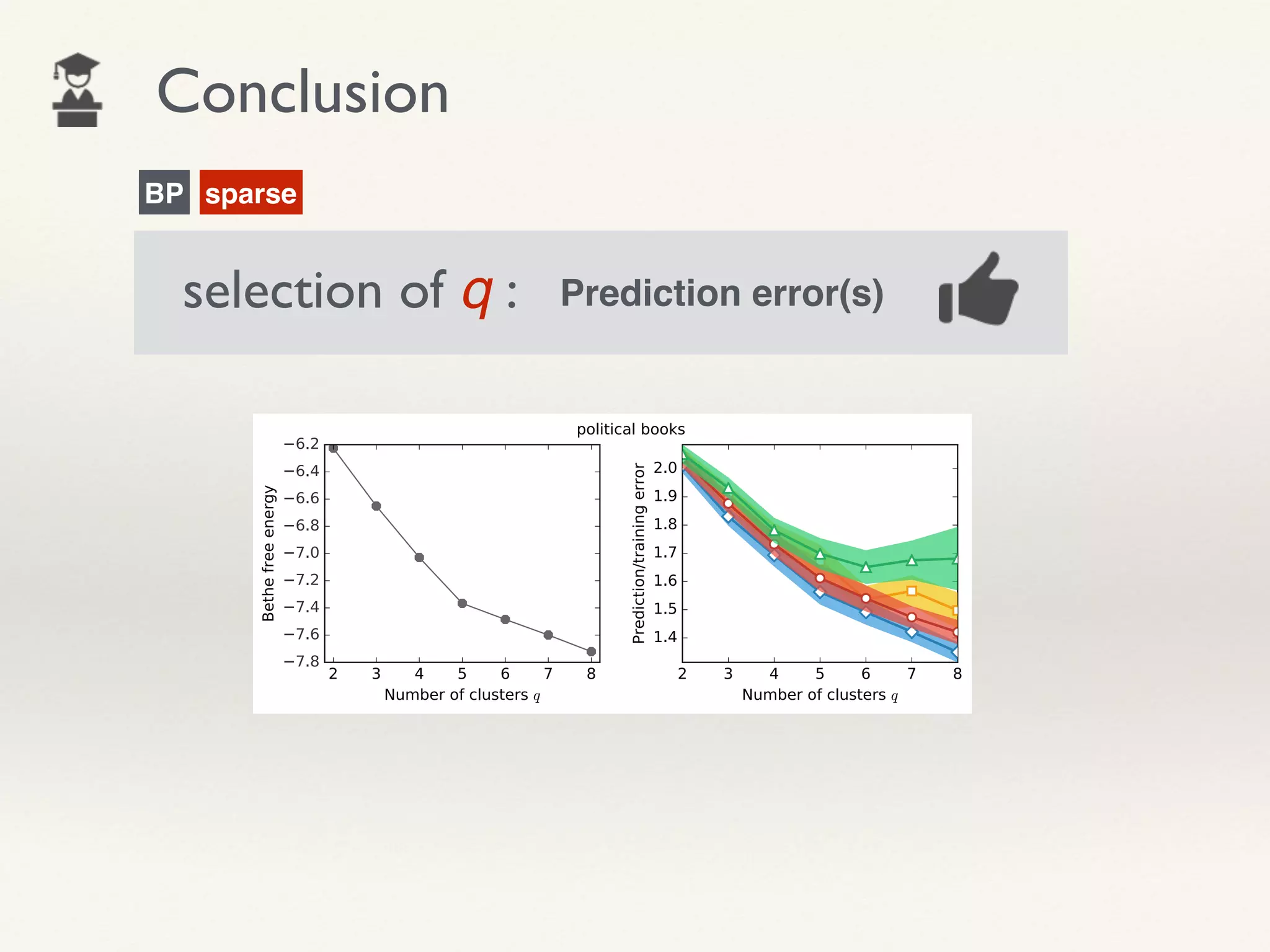
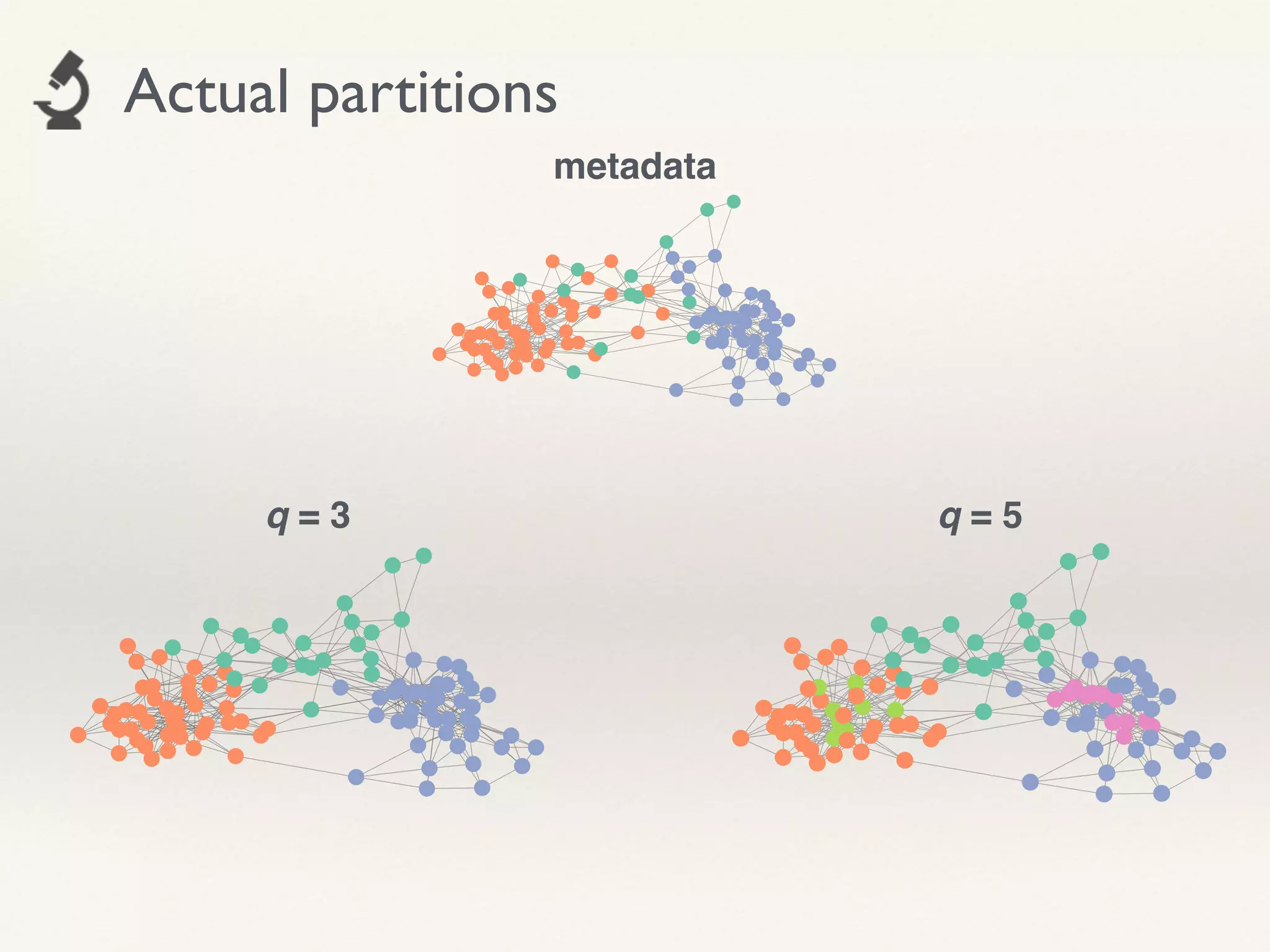
- The document proposes using leave-one-out cross-validation (LOOCV) estimates of prediction errors to select the number of clusters (q) in community detection on networks. - It considers 4 types of LOOCV estimates calculated efficiently using Belief Propagation, and analyzes their theoretical properties. - The approach is shown to perform reasonably in practice on example networks, providing a principled and scalable method for selecting q.

1. Cross-validation estimate of !
the number of clusters in a network
AIST
Scientific Reports 7, 3327 (2017). arXiv:1605.07915 (2016).
Tatsuro Kawamoto
1
“Comparative analysis on the selection of number of clusters in community detection”,!
T.K., Y. Kabashima, arXiv:1606.07668 (2016).
related work
Tokyo Tech Yoshiyuki Kabashima

2. Graph clustering (community detection)
Books about US politics
Determine the number of clusters q that
most efficiently describes the network.
Goal

3. Framework: statistical inference!
Model: Stochastic Block Model!
Algorithm: EM algorithm + Belief Propagation (BP)!
!
Selection of q (model selection): !
LOOCV estimates of prediction errors
Summary
• 4 types of the LOOCV estimates prediction/training errors are considered.
• The LOOCV can be performed efficiently using BP.
• Performance is reasonable in practice.
• Overfit/underfit tendency among the LOOCVs is analyzed theoretically.
(LOOCV = leave-one-out cross-validation)
Principled, scalable, and widely applicable.

4. ω : connection prob. (affinity matrix)
q : # of clusters
γ : sizes of clusters
p(A, | , !, q) =
NY
i=1
i
Y
i<j
!Aij
i j
1 ! i j
1 Aij
Aij : adjacency matrix
σi : the cluster that vertex i belongs
Stochastic block model (SBM)

5. f =
1
N
log
X
p(A, | , !)
j
i k
i
i
=
1
Zi i
e h i
Y
k2@i
X
k
k!i
k
! k i
!
i!j
i
=
1
Zi!j i
e h i
Y
k2@ij
X
k
k!i
k
! k i
!
Belief Propagation (BP)
Minimize the (Bethe) free energy
using the EM algorithm
p(A, | , !, q) =
NY
i=1
i
Y
i<j
!Aij
i j
1 ! i j
1 Aij
Marginal distribution of σ w.r.t. vertex i
i
i
Decelle et al., PRE (2011) BP sparsePartial Bayes

6. Previous works
Decelle et al., PRE (2011)
Scalable algorithm in sparse case!
High accuracy in the ideal situation (known theoretically)!
!
but the Bethe free energy typically fails to determine q in practice
We keep the algorithm and use
prediction errors to determine q
BP sparse
we focus on
Partial Bayes
can’t select q…

7. test settraining set
Prediction error
example
error
model complexity
prediction error
training error
most parsimonious
total dataset
predict test set from training set

8. test settraining set
Prediction error
training settraining set test set
test settraining set
test set training set
3-fold cross-validation
total dataset

9. test set
dataset
i j
edge
test set
non-edge
?i j
{Aij}
…
?
i
j
training set
training set
Leave-one-out cross-validation
very heavy computation
(if it is done by brute force)

10. Bayes prediction error
?i j
cross-entropy error function
EBayes(q) =
1
L
X
i<j
pactual(Aij)
h
log ˆp(Aij|A(i,j)
)
i
Analytic Expression in terms of BP!!
(i.e., no need of brute force!)
i j
σ are marginalized
ˆp(Aij = 1|A(i,j)
) =
X
i, j
ˆp(Aij = 1| i, j)p( i, j|A(i,j)
)
=
X
i, j
! i j
i!j
i
j!i
j

11. Gibbs prediction error
EGibbs(q) =
1
L
X
(i,j)2E
X
i, j
i!j
i
j!i
j
log ! i j
i!j
i
! i,argmax{ i!j
}
MAP estimate
Gibbs training error
Etraining(q) =
1
L
X
(i,j)2E
X
i, j
i!j
i
! i j
j!i
j
Zij
log ! i j
i j
Measure the error before
marginalizing w.r.t. σ
Choose most likely σ
Use all the data to
measure the error

12. Results
Gibbs prediction
MAP (Gibbs)
Bayes prediction
Gibbs training
political books
Bethefreeenergy
We use the “one-standard error rule.”
Hastie, Tibshirani, & Friedman “Elements of Statistical Learning” (2013)

13. Actual partitions
metadata
q = 3 q = 5

14. Other networks

15. Degree-corrected SBM
Gibbs prediction
MAP (Gibbs)
Bayes prediction
Gibbs training
ba
Political blogspolitical books
un-corrected corrected

16. Relations among errors
EBayes = EGibbs DKL p( i, j|A(i,j))||p( i, j|A)
EBayes = Etraining + DKL p( i, j|A)||p( i, j|A(i,j))
sample average
qtraining qBayes qGibbs
Etraining  EBayes  EGibbs
If the partitions of different q constitutes a
hierarchical structure (sufficient condition),
deduced from the monotonicity of the KL divergence.
Directly from the Bayes rule,

17. Bethe free energy in terms of the
prediction errors
If we consider the leaf-one-vertex-out version
of the Bayes prediction error,
i
Ev
Bayes(q) =
1
L
X
i
log Zi
fBethe(q) / Ev
Bayes(q) EBayes(q) + const.
Ev
Bayes(q)Note that the error for each edge is counted twice in

18. When the network is actually
generated by the SBM
a b c d e
• The Bayes prediction error achieves the information-theoretic
detectability threshold for q=2 equal-size clusters. (analytically derived)!
!
• The Gibbs prediction error strictly underfits near the detectability
threshold. (analytically derived)

19. Hold-out method & K-fold CV
10-fold cross-validationholdout method
network scienceb
holdout method 10-fold cross-validation
political booksa It is possible to perform the hold-out
method and the K-fold CV using BP.
But they have both
computational and conceptual
issues.
Their performances look nice indeed.
Orders of magnitude heavier than the LOOCV!

20. Codes are on GitHub
https://github.com/tatsuro-kawamoto/graphBIX
sbm.jl SBM!
mod.jl simpler one
（with&without degree-correction）

21. Conclusion
BP sparse
Prediction error(s)selection of q :