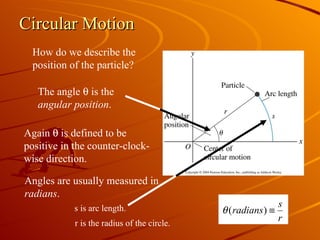
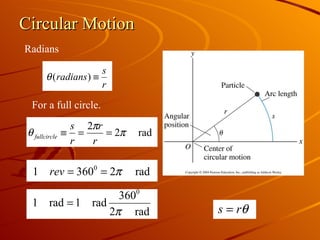
The document discusses uniform circular motion and related concepts. It describes uniform circular motion as a particle moving at constant speed in a circle. It also discusses angular position, angular velocity, centripetal acceleration, coordinate systems used to analyze circular motion, and problem-solving strategies for circular motion problems.