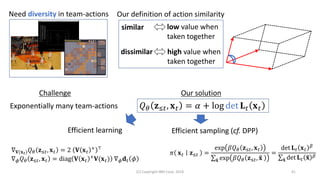
This document discusses the integration of diversity into reinforcement learning and machine learning, emphasizing its significance in collaborative multi-agent environments. It explores methods for enhancing action-value functions by incorporating the concept of diversity, particularly through the utilization of determinantal point processes. The proposed approach demonstrates efficient learning and sampling strategies that account for both value and action diversity in decision-making scenarios.
















![Prior work uses free-energy of restricted
Boltzmann machines [Sallans & Hinton 2001]
(C) Copyright IBM Corp. 2018 21
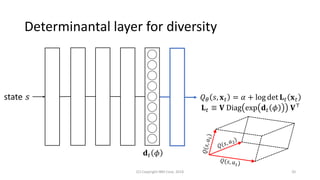
state 𝑠
hidden units
𝐱
𝐹 𝐱 = − log
ሚ𝐡
exp −𝐸 𝐱, ሚ𝐡
𝐸 𝐱, 𝐡 ≡ −𝐛⊤
𝐱 − 𝐜⊤
𝐡 − 𝐱⊤
𝐖𝐡
𝐹 𝐱 = −𝐛⊤ 𝐱
No hidden units
𝐡 Bias 𝐛 represents individual
value of each action](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-21-320.jpg)




![Determinantal SARSA finds a nearly optimal
policy 10 times faster than baseline methods
(C) Copyright IBM Corp. 2018 26
[Heese+ 2013]
SARSA: Free-energy SARSA
NN: Neural network
EQNAC: Energy-based Q-value natural actor critic
ENATDAC: Energy-based natural TD actor critic
Determinantal SARSA](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-26-320.jpg)

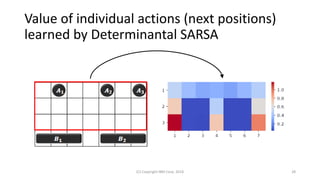
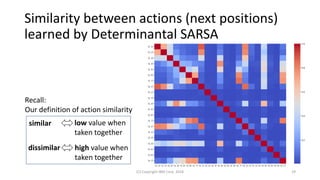
![Determinantal SARSA finds nearly optimal policies,
while baselines suffer from partial observability
(C) Copyright IBM Corp. 2018 31
(𝑁 = 5) (𝑁 = 6) (𝑁 = 8)
SARSA: Free-energy SARSA
NN: Neural network
EQNAC: Energy-based Q-value natural actor critic
ENATDAC: Energy-based natural TD actor critic
Determinantal SARSA Determinantal SARSA Determinantal SARSA
Baselines from [Heese+ 2013]](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-31-320.jpg)




![Determinantal point process (DPP) has been
studied for modeling and learning diversity
• Probability of selecting a subset 𝒳 [Macchi 1975]:
ℙ 𝒳 =
det 𝐋 𝒳
σ 𝒳
det 𝐋 𝒳
=
det 𝐋 𝒳
det 𝐋 + 𝐈
• Sampling in 𝑂 𝑁 𝑘3
time [Hough+ 2006]
• 𝑁: size of ground set
• 𝑘: number of items in sampled subset
(C) Copyright IBM Corp. 2018 36
[Kulesza & Taskar (2012)]](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-36-320.jpg)
![Prior work has been applying DPPs in
machine learning and artificial intelligence
• Recommendation [Gillenwater+ 2014, Gartrell+ 2017]
• Summarization of document, videos, … [Gong+ 2014]
• Hyper-parameter optimization [Kathuria+ 2016]
• Mini-batch sampling [Zhang+ 2017]
• Modeling neural spiking [Snoek+ 2013]
(C) Copyright IBM Corp. 2018 37](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-37-320.jpg)
![Nearly exact Boltzmann exploration with
MCMC [Kang 2013 (for 𝛽 = 1)]
1. Initialize 𝐱
2. Repeat
• 𝐱 ← 𝐱′ with probability min 1,
det 𝐋 𝑡 𝐱′
det 𝐋 𝑡 𝐱
𝛽
• When 𝐱’ and 𝐱 differs by one bit, det 𝐋 𝑡 𝐱′
can be computed from
det 𝐋 𝑡 𝐱 via rank-one update techniques
• Assume we can find 𝑎 ← 𝜓−1(𝐱)
(C) Copyright IBM Corp. 2018 38](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-38-320.jpg)
![Simpler approaches:
Heuristics for more exploration and exploitation
• For more exploration
• Uniform with probability 𝜀
• DPP with probability 1 − 𝜀
• For more exploitation
• Sample 𝑀 actions according to DPP
• Choose the best among 𝑀
• Hard-core point processes [Matérn 1986]
(C) Copyright IBM Corp. 2018 39](https://image.slidesharecdn.com/stairlab-20181116-181122055014/85/19-39-320.jpg)