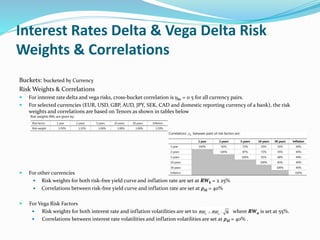
The document discusses the standardized approach for calculating counterparty credit valuation adjustment (SA-CVA) capital under Basel regulations. It provides details on the sensitivities based charge calculation method for SA-CVA, including delta and vega risk charges across different risk classes. It also outlines the risk weights and correlations used to calculate delta and vega risk charges for various risk factors like interest rates, credit spreads, equities, foreign exchange, and commodities.

1. Ramesh Jonnadula

2. Standardised Approach for CVA (SA-CVA)
 Two approaches are available for calculating CVA capital: the standardised approach (SA-CVA) and
the basic approach (BA-CVA). Banks must use the BA-CVA unless they receive approval from their
relevant supervisory authority to use the SA-CVA
 Banks that have received approval of their supervisory authority to use the SA-CVA may carve out
from the SA-CVA calculations any number of netting sets. CVA capital for all carved out netting sets
must be calculated via the BA-CVA
 Any bank whose aggregate notional amount of noncentrally cleared derivatives is less than or equal to
100 billion euro is deemed as being below the materiality threshold. Any bank below the materiality
threshold may choose to set its CVA capital equal to 100% of the bank’s capital requirement for
counterparty credit risk (CCR). CVA hedges are not recognised under this treatment. If chosen, this
treatment must be applied to the bank’s entire portfolio instead of the BA-CVA or the SA-CVA. A
bank’s relevant supervisory authority, however, can remove this option if it determines that CVA risk
resulting from the bank’s derivative positions materially contributes to the bank’s overall risk
 SA-CVA is meant for Banks that have a dedicated CVA Desk. The scope of this document is limited to
SA-CVA
 The standardised approach for CVA (SA-CVA) is an adaptation of the standardised approach for
Market risk (SA-TB) under FRTB.
 SA-CVA does not include default risk and curvature risk
 Regulatory CVA must be calculated as the expectation of future losses resulting from default of the
counterparty under the assumption that the bank itself is default risk-free. The calculation must be
based on at least the following inputs: (i) term structure of market implied probability of default
(PD); (ii) market-consensus expected loss given default (ELGD); (3) simulated paths of discounted
future exposure.
 If an instrument is deemed as an eligible hedge for credit spread delta risk, it must be assigned in its
entirety either to the counterparty credit spread or to the reference credit spread (ie credit spreads
that drive exposure) risk type. Instruments cannot be split between the two risk types.

3. Capital Charge (SA-CVA) under
Standardised Approach
Sensitivities based Charge (SBC)
The SA-CVA capital requirement is calculated as the sum of the capital requirements for
delta and vega risks calculated for the entire CVA portfolio (including eligible hedges).
Sensitivities based Charge for a given Correlation Scenario = sum of Delta and Vega Risk Charges
across all Risk Classes (IR, Cpty Credit, Ref Credit, EQ, FX & CM)
which is
Delta Risk Charge(IR) + Vega Risk Charge(IR)
+ Delta Risk Charge(Cpty Credit Spread)
+ Delta Risk Charge(Reference Credit Spread) + Vega Risk Charge(Reference Credit Spread)
+ Delta Risk Charge(EQ) + Vega Risk Charge(EQ)
+ Delta Risk Charge(FX) + Vega Risk Charge(FX)
+ Delta Risk Charge(CM) + Vega Risk Charge(CM)

4. SBC – Delta & Vega Risk Charges
Delta &Vega Risk Charges
 For a given risk type, calculate the sensitivity of the aggregate CVA, 𝑠 𝑘
CVA, and the
sensitivity of the market value of all eligible hedging instruments in the CVA portfolio, 𝑠 𝑘
Hdg, to each risk factor k in the risk type.
 Obtain the weighted sensitivities WS 𝑘
CVA and WS 𝑘
Hdg for each risk factor k by multiplying
the net sensitivities 𝑠 𝑘
CVA and 𝑠 𝑘
Hdg, respectively, by the corresponding risk weight RW 𝑘
WS 𝑘
CVA = RW 𝑘 .WS 𝑘
CVA WS 𝑘
Hdg = RW 𝑘 .WS 𝑘
Hdg
 The net weighted sensitivity of the CVA portfolio sk to risk factor k is obtained via:
WS 𝑘 =WS 𝑘
CVA + WS 𝑘
Hdg
 Group the Riskfactors in a given Risk Class into buckets. The risk position for Delta
bucket b (respectively Vega), 𝐾 𝑏, computed using correlation between riskfactors (𝜌 𝑘l)
using the following formula:
where R is the hedging disallowance parameter, set at 0.01, that prevents the possibility of
perfect hedging of CVA risk
 The Delta (respectively Vega) risk charge for a given Risk Class (IR, CR, ..) is computed
using bucket correlations (γbc):

5. Appendix

6. Interest Rates Delta & Vega Delta Risk
Weights & Correlations
Buckets: bucketed by Currency
Risk Weights & Correlations
 For interest rate delta and vega risks, cross-bucket correlation is γbc = 0 5 for all currency pairs.
 For selected currencies (EUR, USD, GBP, AUD, JPY, SEK, CAD and domestic reporting currency of a bank), the risk
weights and correlations are based on Tenors as shown in tables below
 For other currencies
 Risk weights for both risk-free yield curve and inflation rate are set at RWk = 2 25%
 Correlations between risk-free yield curve and inflation rate are set at 𝜌 𝑘l = 40%
 For Vega Risk Factors
 Risk weights for both interest rate and inflation volatilities are set to where RWσ is set at 55%.
 Correlations between interest rate volatilities and inflation volatilities are set at 𝜌 𝑘l = 40% .

7. Counterparty Credit Spreads Risk Weights
& Correlations
Buckets: bucketed by Sector and Credit Quality (as shown in the table below)
For Counterparty Credit Spread, Vega risk is ignored, only Delta risk is included
Risk Weights
 Risk weights RWk are same for all tenors and depend on the entity’s bucket and Credit Quality
 For cross-bucket correlations γbc applying across bucket 7 and another bucket, γbc = 0%
 Correlations 𝜌 𝑘l between different tenors for the same entity are set to 90%
 For entities that are legally related:
 Correlations 𝜌 𝑘l between the same tenors are set to 90%.
 Correlations 𝜌 𝑘l between different tenors are set to 81%.
 For unrelated entities of the same credit quality (IG and IG or HY/NR and HY/NR):
 Correlations 𝜌 𝑘l between the same tenors are set to 50%.
 Correlations 𝜌 𝑘l between different tenors are set to 45%.
 For unrelated entities of different credit quality (IG and HY/NR):
 Correlations 𝜌 𝑘l between the same tenors are set to 40%.
 Correlations 𝜌 𝑘l between different tenors are set to 36%.

8. Reference Credit Spreads Risk Weights &
Correlations
Buckets: bucketed by Sector and Credit Quality (as shown in the table below)
For reference credit spreads, both delta and vega risks are calculated. Buckets for delta and vega risks and cross-bucket correlations
are as shown below
Risk Weights
 Risk weights RWk for Delta Riskfactors are same for all tenors and depend on the entity’s bucket and Credit Quality
 Risk weights for reference credit spread volatilities are set to , where RWσ is set at 55%.
 For cross-bucket correlations γbc applying across IG and HY&NR categories, these correlations are divided by 2
 For cross-bucket correlations γbc applying across bucket 15 and another bucket, γbc is set to 0%.

9. Equity Delta Risk Weights & Correlations
Buckets: bucketed by Economy, Sector and Market Cap.
 Large Market Cap: Market Capitialization >= $2 billion, otherwise Small Cap
 The advanced economies are Canada, the United States, Mexico, the euro area, the non-euro area western European
countries (the United Kingdom, Norway, Sweden, Denmark and Switzerland), Japan, Oceania (Australia and New
Zealand), Singapore and Hong Kong SAR
 For equity delta and vega risks, cross-bucket correlation γbc = 15% for all cross-bucket pairs that fall within bucket
numbers 1 to 10. γbc = 0% for all cross-bucket pairs that include bucket 11.
 Risk weights for equity volatilities are set to for large capitalisation buckets and to for small
capitalisation buckets, where RWσ is set at 55%

10. Commodity Delta Risk Weights &
Correlations
Buckets & Risk Weights: bucketed by grouping commodities with similar characteristics
 For commodity delta and vega risks, cross-bucket correlation γbc = 20% for all cross-bucket pairs that fall within bucket
numbers 1 to 10. γbc = 0% for all cross-bucket pairs that include bucket 11.
 Risk weights for commodity volatilities are set to , where RWσ is set at 55%.

11. FX Delta & Vega Risk Weights &
Correlations
Buckets : Currency in which an instrument is denominated and the reporting currency (Currency pair)
Risk Weights
 For FX delta and vega risks, cross-bucket correlation is γbc = 0.6 for all currency pairs
 Risk weights for all foreign-domestic exchange rates are set at RWk = 21%
 Risk weights for FX volatilities are set to σ = , where RWσ is set at 55%.

12. Acknowledgements
Most of the content is sourced from Basel III – Finalising post-crisis reforms