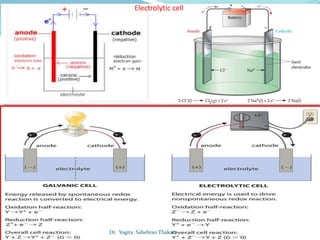
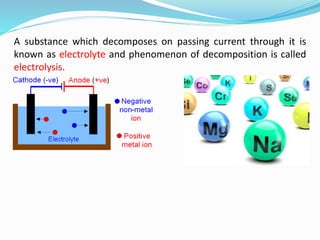
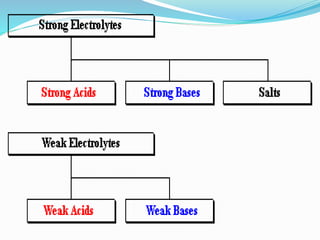
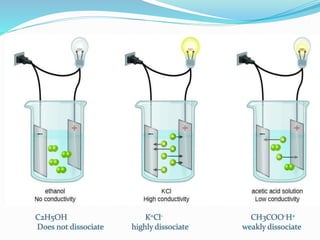
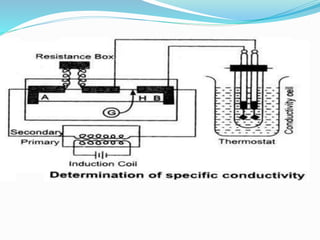
The document discusses electrochemistry, focusing on concepts such as conductance, specific conductance, equivalent conductance, and molar conductance, along with their definitions and formulas. It explains how to determine conductance using the Wheatstone bridge method and details the behavior of conductance with dilution. Various examples are provided to illustrate calculations related to specific and equivalent conductance in electrolytic solutions.

1. Dr. Y. S. THAKARE
M.Sc. (CHE) Ph D, NET, SET
Assistant Professor in Chemistry,
Shri Shivaji Science College, Amravati
Email: yogitathakare_2007@rediffmail.com
B Sc- II Year
SEM-III
PAPER-III
PHYSICAL CHEMISTRY
UNIT- VI
Introduction to electrochemistry
16-October -20 1

2. Education is the most powerful weapon
which you can use to change the world.
-Nelson Mandela
Be kind whenever possible. It is always
possible.
-Dalai Lama
There is no substitute for hard work.
-Thomas A. Edison

3. Electrochemistry: The Branch of physical chemistry which
deals with the study of interconversion of electrical energy
in to chemical energy or vice-versa
Electrolytic Cell: Conversion of electrical energy in to
chemical energy
Electrochemical Cell: Conversion of chemical energy into
electrical energy
Electrode – The metal rod dipped in its salt solution

4. Electrolytic cell
Dr. Yogita Sahebrao Thakare

5. A substance which decomposes on passing current through it is
known as electrolyte and phenomenon of decomposition is called
electrolysis.

10. Conductance of electrolyte solutions:
The capacity of conductor to carry the electrical current
(energy) is known as the conductance or conductivity. We generally
come across with two conductors i.e. metallic and electrolytic
conductors.
The conductance of electrolyte solution is due to migration of ions
through the solution to the electrodes. The conductance (C) of an
electrolyte is the reciprocal of its resistance (R).
Thus, 𝐶 =
1
𝑅
It is measured in ohm-1 or mho or Siemens (S).
Resistance of any uniform conductor varies directly as its
length and inversely to its area of cross section.
R ∝
𝑙
𝑎
OR R = ρ
𝑙
𝑎
Where, ρ = constant called specific resistance or resistivity
l = length of conductor
a = cross sectional area of conductor

11. R = ρ
𝑙
𝑎
When l = a = 1,
R = ρ
Hence, specific resistance is the resistance of
length and unit cross sectional area
OR It is the resistance of 1 m3 material.

12. Specific conductance (  ): “The conductance of one centimeter
cube (1 cm3) or one cubic meter (1 m3) solution of an electrolyte
an electrolyte is known as specific conductance.” It is denoted by
is denoted by ‘ ’ (Kappa).
Specific conductance () is reciprocal of specific resistance (ρ).
.˙.

13. For electrolytes specific conductance is the conductance of one
meter cube of solution.
Unit of Conductance
We know that
 = C
𝑙
𝑎
CGS unit
 = 𝑜ℎ𝑚−1
𝑐𝑚
𝑐𝑚2
= 𝑜ℎ𝑚−1𝑐𝑚−1 = 𝑚ℎ𝑜 𝑐𝑚−1 = 𝑆𝑐𝑚−1
SI Unit
 = 𝑜ℎ𝑚−1
𝑚
𝑚2
= 𝑜ℎ𝑚−1
𝑚−1
= 𝑚ℎ𝑜 𝑚−1
= 𝑆𝑚−1
Its CGS unit is ohm-1 cm-1 or S cm-1 & SI unit is ohm-1 m-1 or S m-1.

14. Equivalent conductance : It is defined as the conductance of a
solution containing one Kg equivalent of electrolyte placed between
placed between two parallel electrodes 1 meter apart. It is denoted
It is denoted by 𝑣 .
OR
“The conductance of one gram equivalent of an electrolyte, dissolved
electrolyte, dissolved in ‘V’cc of water.”
It is the product of specific conductivity and the volume of solution
containing 1 kg equivalent of electrolyte.
𝑣 =  V
In general, if an electrolyte solution contains ‘N’ gram equivalent in
1000 cc of solution. Then,
𝑣 =
 × 1000
𝑁

15. Unit of Equivalent conductance
We know that
𝑣 =
 × 1000
𝑁
CGS unit
𝑣 =
𝑆𝑐𝑚−1 × 𝑐𝑚3
𝑒𝑞
= 𝑆𝑐𝑚2
𝑒𝑞−1
= 𝑜ℎ𝑚−1
𝑐𝑚2
𝑒𝑞−1
= 𝑚ℎ𝑜 𝑐𝑚2𝑒𝑞−1
SI Unit
𝑣 =
𝑆𝑚−1 × 𝑚3
𝑒𝑞
= 𝑆𝑚2𝑒𝑞−1 = 𝑜ℎ𝑚−1𝑚2𝑒𝑞−1 = 𝑚ℎ𝑜 𝑚2𝑒𝑞−1
In CGS system its unit is mho cm2 eq-1 or S cm2 eq-1. The SI unit of
equivalent conductance is mho m2 eq-1 or S m2 eq-1

16. Molar conductance (µ𝑣): “It is defined as conductance of solution
containing one mole of electrolyte placed between two parallel
parallel electrodes one meter apart.” It is denoted by (µ𝑣 ).
).
OR
“The conductance of the solution containing one gram mole of
mole of electrolyte is known as molar conductance”.
If one gram mole of electrolyte dissolved in ‘V’cc of solution, then its
molar conductance is given as
µ𝑣 =  V
 = specific conductance
V = volume of solution in meter cube containing 1 gm molecular
molecular weight of an electrolyte.
µ𝑣 =
 × 1000
𝑀

17. Unit of Molar Conductance
We know that
µ𝑣 =
 × 1000
𝑀
CGS unit
µ𝑣 =
𝑆𝑐𝑚−1
× 𝑐𝑚3
𝑚𝑜𝑙
= 𝑆𝑐𝑚2
𝑚𝑜𝑙−1
= 𝑜ℎ𝑚−1
𝑐𝑚2
𝑚𝑜𝑙−1
= 𝑚ℎ𝑜 𝑐𝑚2𝑚𝑜𝑙−1
SI Unit
µ𝑣 =
𝑆𝑚−1 × 𝑚3
𝑚𝑜𝑙
= 𝑆𝑚2
𝑚𝑜𝑙−1
= 𝑜ℎ𝑚−1
𝑚2
𝑚𝑜𝑙−1
= 𝑚ℎ𝑜 𝑚2
𝑚𝑜𝑙−1
In CGS system its unit is mho cm2 𝑚𝑜𝑙 -1 or S cm2 𝑚𝑜𝑙 -1. The SI unit of
equivalent conductance is mho m2 eq-1 or S m2 𝑚𝑜𝑙 -1

18. Determination of conductance of electrolyte solution using
Wheatstone bridge method :
Conductance of an electrolytic solution is the reciprocal of
resistance (C=1/R). Therefore, measurement of conductance is
done indirectly by determining the resistance of the solution. The
resistance is measured by Wheatstone AC bridge method. Direct
current cannot be used in this process as this will give wrong result
due to
1. Change in concentration due to electrolysis.
2. Change in resistance due to polarization at electrodes

20. These difficulties are overcome by using alternating current within
audio frequency range and galvanometer in Wheatstone bridge is
replaced by headphone. The schematic diagram of the apparatus is
shown in fig.
The solution whose conductivity is to be determined is taken in a
suitable conductivity cell ‘C’. When current is flowing know resistance
‘R’ is introduced through resistance box. The sliding contact ‘X’ is then
moved along the wire ‘AB’ of uniform thickness until a point of
minimum sound is detected in headphone (G). At this stage,
𝑅𝑒𝑠𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑜𝑓 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
𝑅𝑒𝑠𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑓𝑟𝑜𝑚 𝑟𝑒𝑠𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑏𝑜𝑥
=
𝐿𝑒𝑛𝑔𝑡ℎ 𝐵𝑋
𝐿𝑒𝑛𝑔𝑡ℎ 𝐴𝑋
As all values from above equation are known, resistance of solution
can be determined. From this resistance, conductance of solution can
be determined.

21. Determination of cell constant:
Cell constant () is defined as the ratio of length (distance) between the
electrodes ‘l’ and area of cross section ‘a’ of electrode.
𝐶𝑒𝑙𝑙 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 =  =
𝑙
𝑎
In order to determine cell constant () it is necessary to determine ‘l’ & ‘a’.
But actually it is not possible. So indirect method based on measurement of
conductance of standard KCl solution is employed as follows:
We know that
 = C
𝑙
𝑎
Specific conductance = Observed conductance × 𝐶𝑒𝑙𝑙 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
To determine the cell constant, a standard solution of KCl of known specific
conductance at a given temperature is used. Its conductance is determined
experimentally at the same temperature. Substituting the two values in
above equation, the cell constant can be calculated.

22. Variation of specific and equivalent conductance with
dilution:
The solution of electrolyte conducts electricity due to the
presence of ions. The conductivity at constant temperature is
approximately proportional to number of ions. According to
ionic theory the number of ions increases as the solution of the
electrolyte is progressively diluted. Therefore, equivalent
conductivity increases as the dilution increases.
The specific conductivity decreases on dilution because on
dilution the number of ions per dm3 of solution decreases in spite
of increase in dissociation.
The equivalent and molecular conductivity increases because
these are the product of specific conductivity and volume
containing on gram equivalent or one mole of an electrolyte.
𝑣 =  V
On dilution, decrease in specific conductance is compensated by
increase in volume ‘V’. This behavior can be illustrated from the
table.

23. Important Formulae
1. Specific conductance ( ) = Observed conductance (C) × 𝑪𝒆𝒍𝒍 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕(
𝒍
𝒂
)
2. Cell constant (
𝒍
𝒂
) =
Sp. Conductance ( )
Observe Conductance (C)
3. Equivalent Conductance (λv) = Sp. conductance () × V
4. 𝒗 =
 × 𝟏𝟎𝟎𝟎
𝑵
5. Observed conductance (C) =
𝟏
𝑶𝒃𝒔𝒆𝒓𝒗𝒆𝒅 𝒓𝒆𝒔𝒊𝒔𝒕𝒂𝒏𝒄𝒆(𝑹)
OR C = 1/R
6. Specific conductance() =
𝟏
Specific 𝒓𝒆𝒔𝒊𝒔𝒕𝒂𝒏𝒄𝒆(ρ)
OR  = 1/ρ
7. Molar Conductance(µ𝒗) = Sp. conductance () × V
8. µ𝒗 =
 × 𝟏𝟎𝟎𝟎
𝑴
9. 𝑪𝒆𝒍𝒍 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕 =  =
𝒍
𝒂

24. Example: 1
A conductivity cell was filled with 0.01 M KCl which was known to have specific
conductivity of 0.1404 mho m-1 at 298 K. Its measured resistance at 298 K was 99.3
ohm. When the cell was filled with 0.02M AgNO3, the resistance was 50.3 ohm.
Calculate (i) Cell constant, (ii) Specific Conductance of AgNO3 solution.
Solution: Given that
(i) For 0.01 M KCl,  = 0.1404 mho m-1
T = 298 K
R = 99.3 ohm
We know that
Cell constant =
Sp. Conductance ( )
Observe Conductance
=
0.1404
1/99.3
= 0.1404 × 99.3
= 13.94
(ii) For 0.02 M AgNO3, R = 50.3 ohm
Sp. Conductance ( ) = Cell constant × Observe Conductance
= 13.94 X 1/50.3
= 13.94 X 50.3
= 0.2771 mho m-1

25. Example: 2
0.5 N solution of salt occupying volume between two platinum electrodes
0.0172 m apart and 0.04499 sq. m. area has resistance 25 ohm. Calculate
equivalent conductance of solution.
Solution: Given that
distance between electrodes, l = 0.0172 m
area of cross section of electrode a = 0.04499 sq. m.
resistance of salt solution R = 25 ohm
Concentration of salt solution C = 0.5N
Sp. conductance () = Cell constant × Observed conductance
=
0.0172
0.04499
×
1
25
= 0.3823 × 0.04
= 0.01529 mho 𝑚−1
Equivalent Conductance λv = Sp. conductance × V
𝑣 =
 × 1000
𝑁
=
0.01529 × 1000
0.5
= 0.01529 X 0.04499=30.58 S 𝑚2𝑒𝑞𝑢𝑖−1

26. Example: 3
The resistance of conductivity cell was 7.02 ohm when filled with 0.1 N KCl solution
(k=0.1480 ohm-1 m-1) and 69.2 ohm, when filled with N/100 NaCl solution at same
temperature. Calculate the cell constant and equivalent conductance of NaCl solution.
Solution:
(i) For 0.1 N KCl, R = 7.02 ohm
 = 0.1480 ohm-1 m-1
Cell constant =
Sp. Conductance ( )
Observe Conductance
=
0.1480
1
7.02
= 0.1480 × 7.02
= 1.038 𝑚−1
(ii) For N/100 or 0.01 N NaCl,
R = 69.2 ohm
Sp. conductance () = Cell constant × Observed conductance
= 1.038 X 1 / 69.2
= 0.015 S m-1
=
Equivalent Conductance λv = Sp. conductance × V
𝑣 =
0.015 × 1000
0.01
=15000 𝑚2𝑒𝑞𝑢𝑖−1