Download as PDF, PPTX
Anderson局在入門
- 1.
- 2. • 研究対象とする実験 • 金属絶縁体転移とAnderson局在の直観的描像 •Anderson局在に関する実験 • スケーリング理論によるAnderson転移 • ミクロ理論によるAnderson弱局在 • 纏めと展望 概要
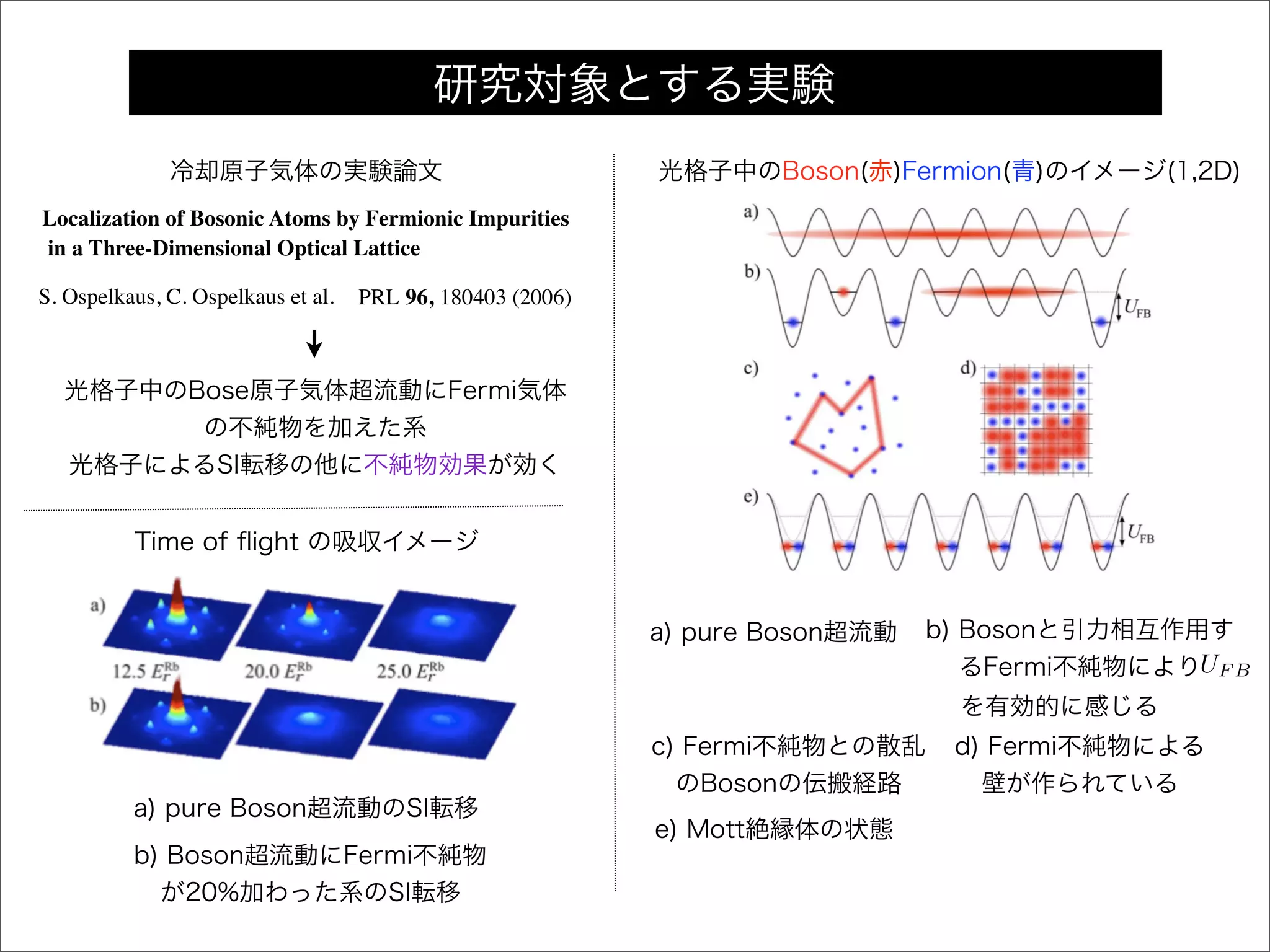
- 3. 研究対象とする実験 Localization of BosonicAtoms by Fermionic Impurities in a Three-Dimensional Optical Lattice PRL 96, 180403 (2006) 光格子中のBose原子気体超流動にFermi気体 の不純物を加えた系 光格子によるSI転移の他に不純物効果が効く S. Ospelkaus, C. Ospelkaus et al. 冷却原子気体の実験論文 a) pure Boson超流動のSI転移 b) Boson超流動にFermi不純物 が20%加わった系のSI転移 Time of flight の吸収イメージ a) pure Boson超流動 b) Bosonと引力相互作用す るFermi不純物によりUF B を有効的に感じる 光格子中のBoson(赤)Fermion(青)のイメージ(1,2D) c) Fermi不純物との散乱 のBosonの伝搬経路 d) Fermi不純物による 壁が作られている e) Mott絶縁体の状態
- 4.
- 5. スケーリング理論について 1958年のAndersonの問題提起があったものの、不規則系の不純物 との散乱、電子の波動関数のふるまいに対しては取り扱いが難しい Anderson局在に対する取り組み 1979年、P. W. Anderson、E.Abrahams、D. C. Licciardello、 T. V. Ramakrishnanの画期的なスケーリング理論が提出される 局在状態の問題としてではなく、試料のコンダクタンス の試料サイズ依存性をみるという新しい視点の理論 スケーリング理論 ？
- 6. スケーリングの仮定 繰り込み群方程式 無次元のコンダクタンスを定義 左辺 右辺 L →νL g(νL) g(L)を求めるにはの下で さえ解っていればよい 両辺対数を取り ln ν で割ると スケーリング理論による繰り込み群方程式の導出 R = ρ L S 3D金属 （ ） コンダクタンスのサイズ依存度が わかる微分方程式になっている
- 7.
- 8.
- 9.
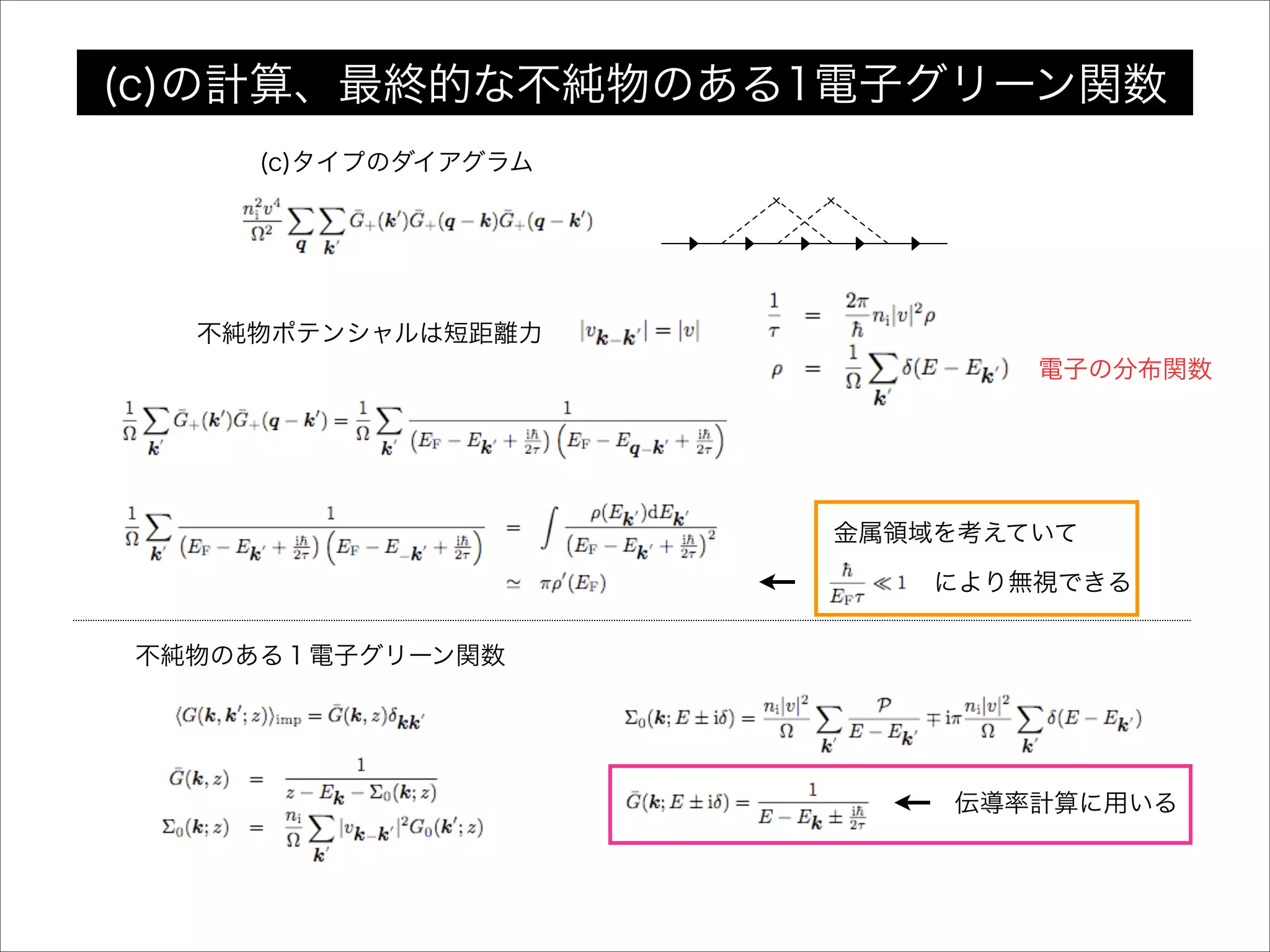
- 10. = + + !! ! … 弱局在の効果を見たいので、金属領域では 不規則ポテンシャルが弱いとして摂動展開 ! ! ! ! imp = ! ! ! ! ! ! + + の下で平均を取ると v は偶数次のみ残る 例：4次の摂動項 (a) (b) (c) 不純物効果を含めた１電子グリーン関数 対象とする系と前提 不純物分布 で存在する金属、また不規則ポテンシャルは弱いとして、短距離力 また3次以上の項では3個以上の の積の平均から、同じ不純物と３回以 上相互作用する項が残るが、不純物の つくるポテンシャルが弱いとして無視 ρk1−k2
- 11. ! ! (a)タイプのダイアグラム Σ0 は自己エネルギー (b)タイプのダイアグラム! ! 自己エネルギー部分に含まれるグリーン関数が 不純物効果を繰り込んだもので置き換えられる (a)(b)のダイアグラム計算
- 12.
- 13. ! ! ! ! ! ! !! ! ! ! ! ! ! ! = + + + ・・・ 電気伝導度の計算に関わるグリーン関数 (a) (b) (c) Drudeの公式 梯子近似 補正摂動項 (b)の梯子型無限級数の第一項 k kと の向きに依存しないので 梯子型はすべて電気伝導度に寄与しない (a)の計算 Drudeの公式と梯子近似 Drudeの公式 imp
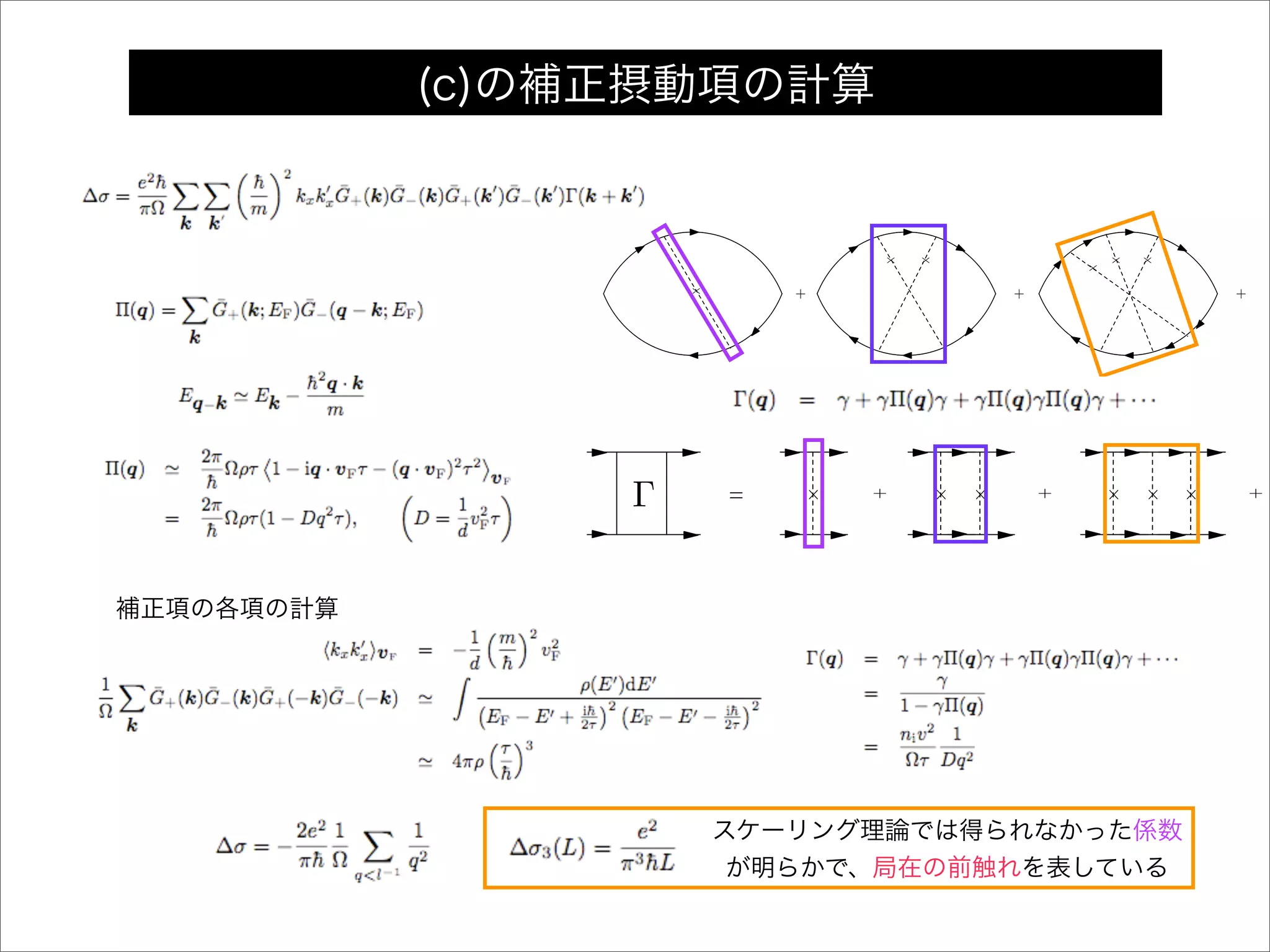
- 14. × ×× ×× × + ++ Γ = × + × × + × × +× (c)の補正摂動項の計算 スケーリング理論では得られなかった係数 が明らかで、局在の前触れを表している 補正項の各項の計算
- 15. • スケーリング理論において弱局在の前触れを見ることができるが、伝導率 の数係数まで求めれない。 • 微視的理論から数係数が得られる •金属系においてAnderson局在の勉強をしたが、さらに金属超伝導おい て不純物効果について調べる • BECに関して、不純物効果の研究をする 纏め 展望
- 16.