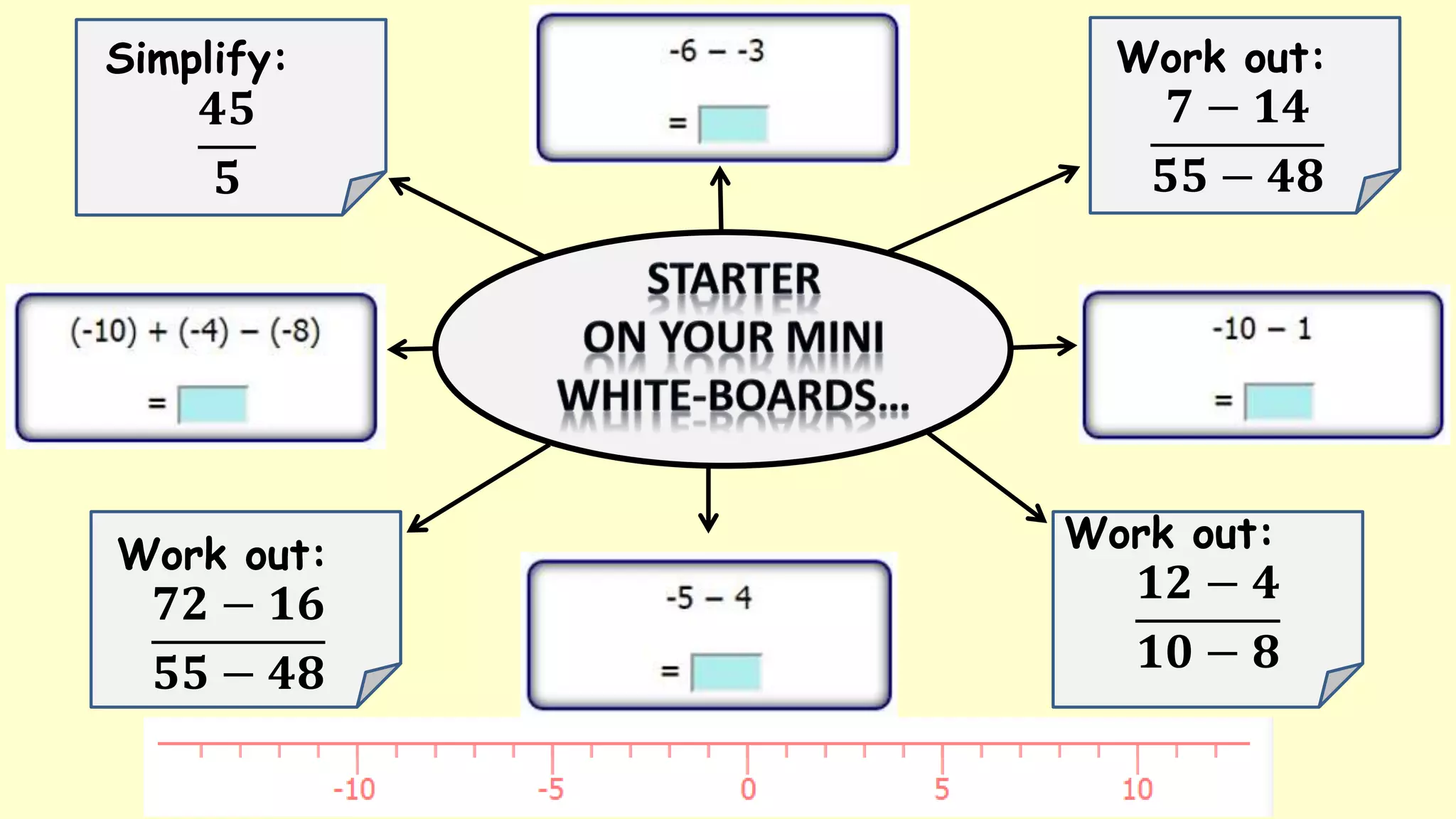
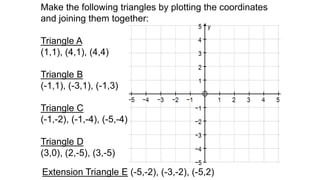
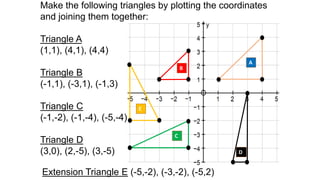
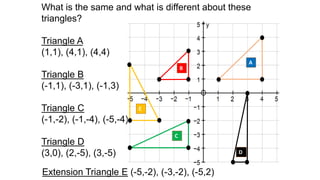
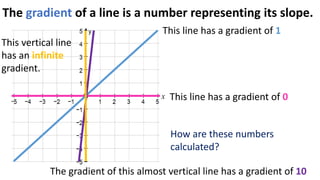
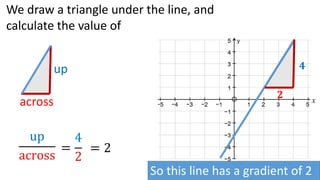
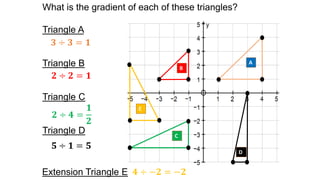
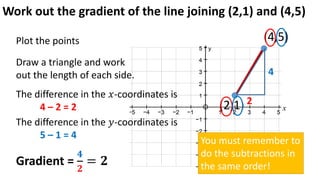
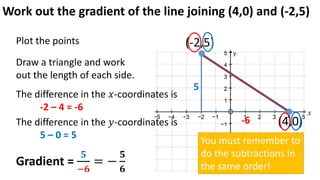
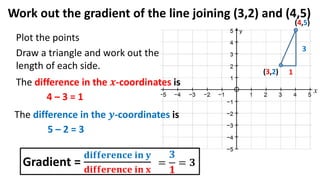
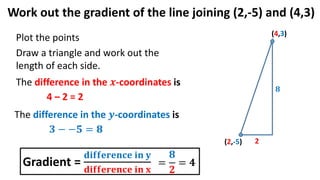
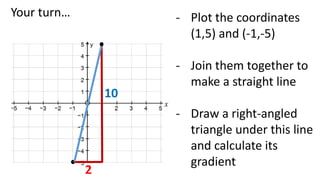
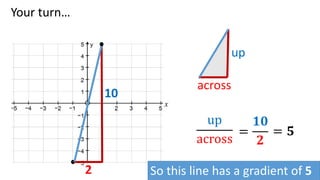
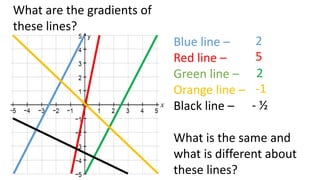
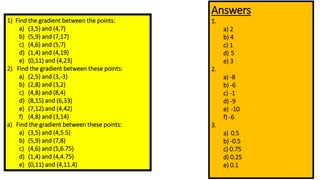
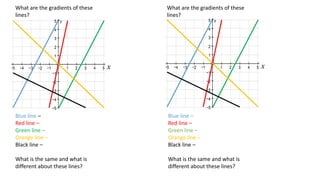
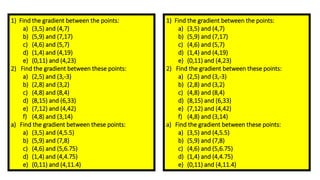
The document discusses calculating the gradient of a line from two coordinate points by drawing a triangle and taking the rise over run. It provides examples of finding the gradient between different point pairs. It also contains practice problems for students to calculate gradients between given points.

1. Work out:
𝟕𝟐 − 𝟏𝟔
𝟓𝟓 − 𝟒𝟖
Work out:
𝟏𝟐 − 𝟒
𝟏𝟎 − 𝟖
Simplify:
𝟒𝟓
𝟓
Work out:
𝟕 − 𝟏𝟒
𝟓𝟓 − 𝟒𝟖

2. LO: Investigate how to find the gradient of a
line given two coordinates
To be able to plot
coordinates in all
four quadrants
To be able to find
the gradient of a
line from a graph
To be able to find
the gradient given
only two
coordinates
GRADIENTS

3. Make the following triangles by plotting the coordinates
and joining them together:
Triangle A
(1,1), (4,1), (4,4)
Triangle B
(-1,1), (-3,1), (-1,3)
Triangle C
(-1,-2), (-1,-4), (-5,-4)
Triangle D
(3,0), (2,-5), (3,-5)
Extension Triangle E (-5,-2), (-3,-2), (-5,2)

4. Make the following triangles by plotting the coordinates
and joining them together:
Triangle A
(1,1), (4,1), (4,4)
Triangle B
(-1,1), (-3,1), (-1,3)
Triangle C
(-1,-2), (-1,-4), (-5,-4)
Triangle D
(3,0), (2,-5), (3,-5)
Extension Triangle E (-5,-2), (-3,-2), (-5,2)
A
D
C
B
E

5. What is the same and what is different about these
triangles?
Triangle A
(1,1), (4,1), (4,4)
Triangle B
(-1,1), (-3,1), (-1,3)
Triangle C
(-1,-2), (-1,-4), (-5,-4)
Triangle D
(3,0), (2,-5), (3,-5)
Extension Triangle E (-5,-2), (-3,-2), (-5,2)
A
D
C
B
E

6. What is the same and what is different about these
triangles?
Triangle A
Triangle B
Triangle C
Triangle D
Extension Triangle E
A
D
C
B
E

10. The gradient of a line is a number representing its slope.
x This line has a gradient of 0
This line has a gradient of 1
The gradient of this almost vertical line has a gradient of 10
How are these numbers
calculated?
This vertical line
has an infinite
gradient.

11. x
We draw a triangle under the line, and
calculate the value of
up
across
up
across
=
4
2
= 2
𝟒
𝟐
So this line has a gradient of 2

12. What is the gradient of each of these triangles?
Triangle A
Triangle B
Triangle C
Triangle D
Extension Triangle E
A
D
C
B
E
𝟑 ÷ 𝟑 = 𝟏
𝟐 ÷ 𝟐 = 𝟏
𝟐 ÷ 𝟒 =
𝟏
𝟐
𝟓 ÷ 𝟏 = 𝟓
𝟒 ÷ −𝟐 = −𝟐

13. x
Work out the gradient of the line joining (2,1) and (4,5)
Plot the points
(2,1)
(4,5)
Draw a triangle and work
out the length of each side.
The difference in the 𝑥-coordinates is
4 – 2 = 2
The difference in the 𝑦-coordinates is
5 – 1 = 4
You must remember to
do the subtractions in
the same order!
2
4
Gradient =
𝟒
𝟐
= 𝟐

14. x
Work out the gradient of the line joining (4,0) and (-2,5)
Plot the points (-2,5)
(4,0)
Draw a triangle and work
out the length of each side.
The difference in the 𝑥-coordinates is
-2 – 4 = -6
The difference in the 𝑦-coordinates is
5 – 0 = 5
You must remember to
do the subtractions in
the same order!
-6
5
Gradient =
𝟓
−𝟔
= −
𝟓
𝟔

15. ON YOUR MINI-WHITEBOARDS…
Work out the gradient of the line joining (3,2) and (4,5)
- Plot the points
- Draw a triangle and work out the length of each side.
- Work out the difference in the 𝒙-coordinates
- Work out the difference in the 𝒚-coordinates
Gradient =
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐲
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐱
Remember to do the
subtractions in the
same order!

16. x
Work out the gradient of the line joining (3,2) and (4,5)
Plot the points
Draw a triangle and work out the
length of each side.
The difference in the 𝒙-coordinates is
The difference in the 𝒚-coordinates is
Gradient =
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐲
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐱
(3,2)
(4,5)
4 – 3 = 1
1
5 – 2 = 3
3
=
𝟑
𝟏
= 𝟑

17. ON YOUR MINI-WHITEBOARDS…
Work out the gradient of the line joining (2,-5) and (4,3)
- Plot the points
- Draw a triangle and work out the length of each side.
- Work out the difference in the 𝒙-coordinates
- Work out the difference in the 𝒚-coordinates
Gradient =
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐲
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐱
Remember to do the
subtractions in the
same order!

18. Work out the gradient of the line joining (2,-5) and (4,3)
Plot the points
Draw a triangle and work out the
length of each side.
The difference in the 𝒙-coordinates is
The difference in the 𝒚-coordinates is
Gradient =
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐲
𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞 𝐢𝐧 𝐱
4 – 2 = 2
𝟑 − −𝟓 = 𝟖
=
𝟖
𝟐
= 𝟒
(2,-5)
(4,3)
2
𝟖

19. End
Easy
Medium
Hard

20. What have we learnt…
To be able to plot
coordinates in all
four quadrants
To be able to find
the gradient of a
line from a graph
To be able to find
the gradient given
only two
coordinates

21. x
Your turn… - Plot the coordinates
(1,5) and (-1,-5)
- Join them together to
make a straight line
- Draw a right-angled
triangle under this line
and calculate its
gradient
10
2

22. x
Your turn…
10
2
up
across
up
across
=
𝟏𝟎
𝟐
= 𝟓
So this line has a gradient of 5

23. x
What are the gradients of
these lines?
Blue line –
Red line –
Green line –
Orange line –
Black line –
What is the same and
what is different about
these lines?
2
5
2
-1
- ½

25. 1) Find the gradient between the points:
a) (3,5) and (4,7)
b) (5,9) and (7,17)
c) (4,6) and (5,7)
d) (1,4) and (4,19)
e) (0,11) and (4,23)
2) Find the gradient between these points:
a) (2,5) and (3,-3)
b) (2,8) and (3,2)
c) (4,8) and (8,4)
d) (8,15) and (6,33)
e) (7,12) and (4,42)
f) (4,8) and (3,14)
a) Find the gradient between these points:
a) (3,5) and (4,5.5)
b) (5,9) and (7,8)
c) (4,6) and (5,6.75)
d) (1,4) and (4,4.75)
e) (0,11) and (4,11.4)
Answers
1.
a) 2
b) 4
c) 1
d) 5
e) 3
2.
a) -8
b) -6
c) -1
d) -9
e) -10
f) -6
3.
a) 0.5
b) -0.5
c) 0.75
d) 0.25
e) 0.1

26. x
What are the gradients of these
lines?
Blue line –
Red line –
Green line –
Orange line –
Black line –
What is the same and what is
different about these lines?
x
What are the gradients of these
lines?
Blue line –
Red line –
Green line –
Orange line –
Black line –
What is the same and what is
different about these lines?

27. 1) Find the gradient between the points:
a) (3,5) and (4,7)
b) (5,9) and (7,17)
c) (4,6) and (5,7)
d) (1,4) and (4,19)
e) (0,11) and (4,23)
2) Find the gradient between these points:
a) (2,5) and (3,-3)
b) (2,8) and (3,2)
c) (4,8) and (8,4)
d) (8,15) and (6,33)
e) (7,12) and (4,42)
f) (4,8) and (3,14)
a) Find the gradient between these points:
a) (3,5) and (4,5.5)
b) (5,9) and (7,8)
c) (4,6) and (5,6.75)
d) (1,4) and (4,4.75)
e) (0,11) and (4,11.4)
1) Find the gradient between the points:
a) (3,5) and (4,7)
b) (5,9) and (7,17)
c) (4,6) and (5,7)
d) (1,4) and (4,19)
e) (0,11) and (4,23)
2) Find the gradient between these points:
a) (2,5) and (3,-3)
b) (2,8) and (3,2)
c) (4,8) and (8,4)
d) (8,15) and (6,33)
e) (7,12) and (4,42)
f) (4,8) and (3,14)
a) Find the gradient between these points:
a) (3,5) and (4,5.5)
b) (5,9) and (7,8)
c) (4,6) and (5,6.75)
d) (1,4) and (4,4.75)
e) (0,11) and (4,11.4)

28. x