Uploaded byJaysonPalma4
20 views

Unit II-Lesson 3- Dihedral and Multiplicative Groups (PALMA).pdf

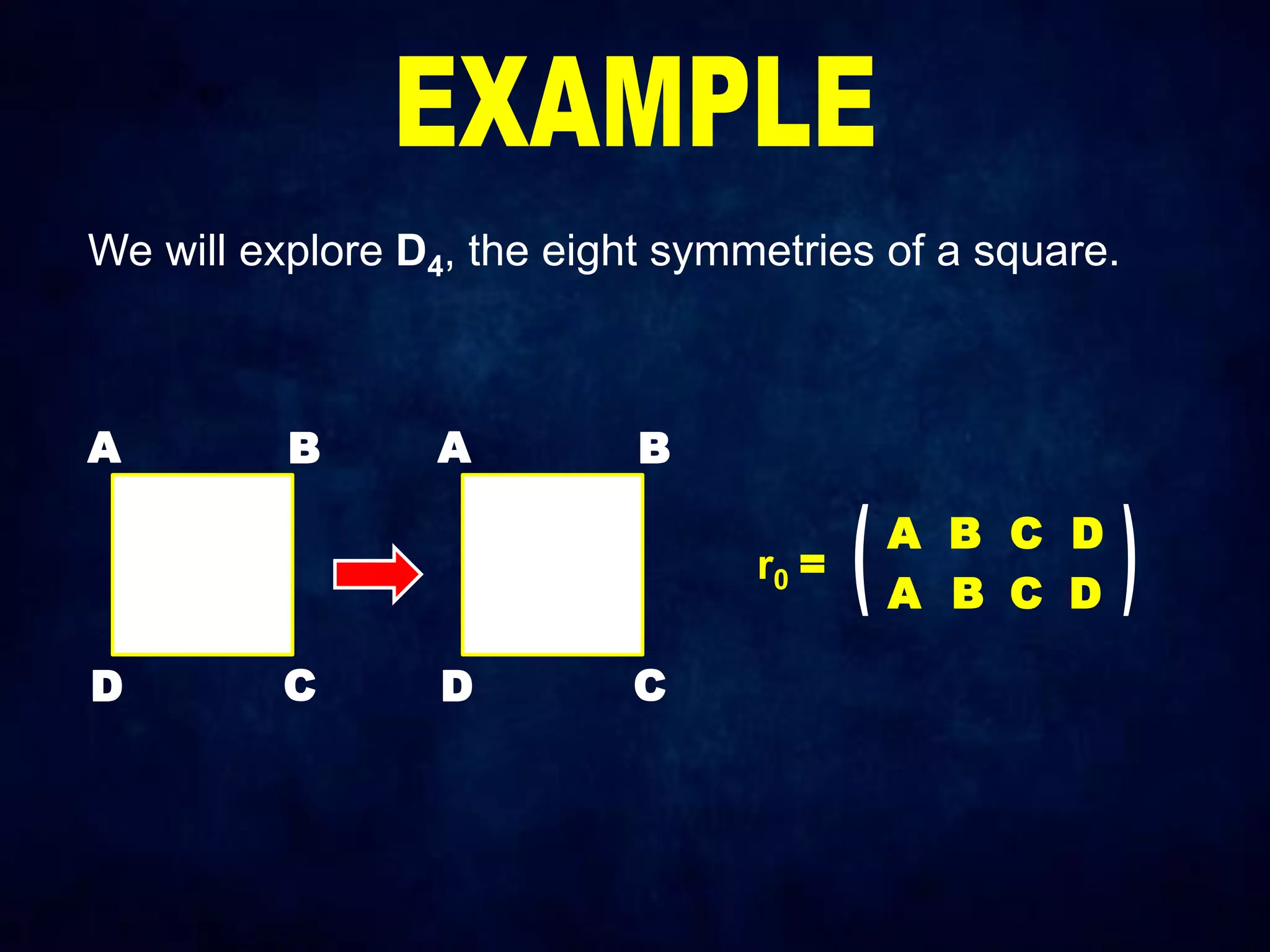
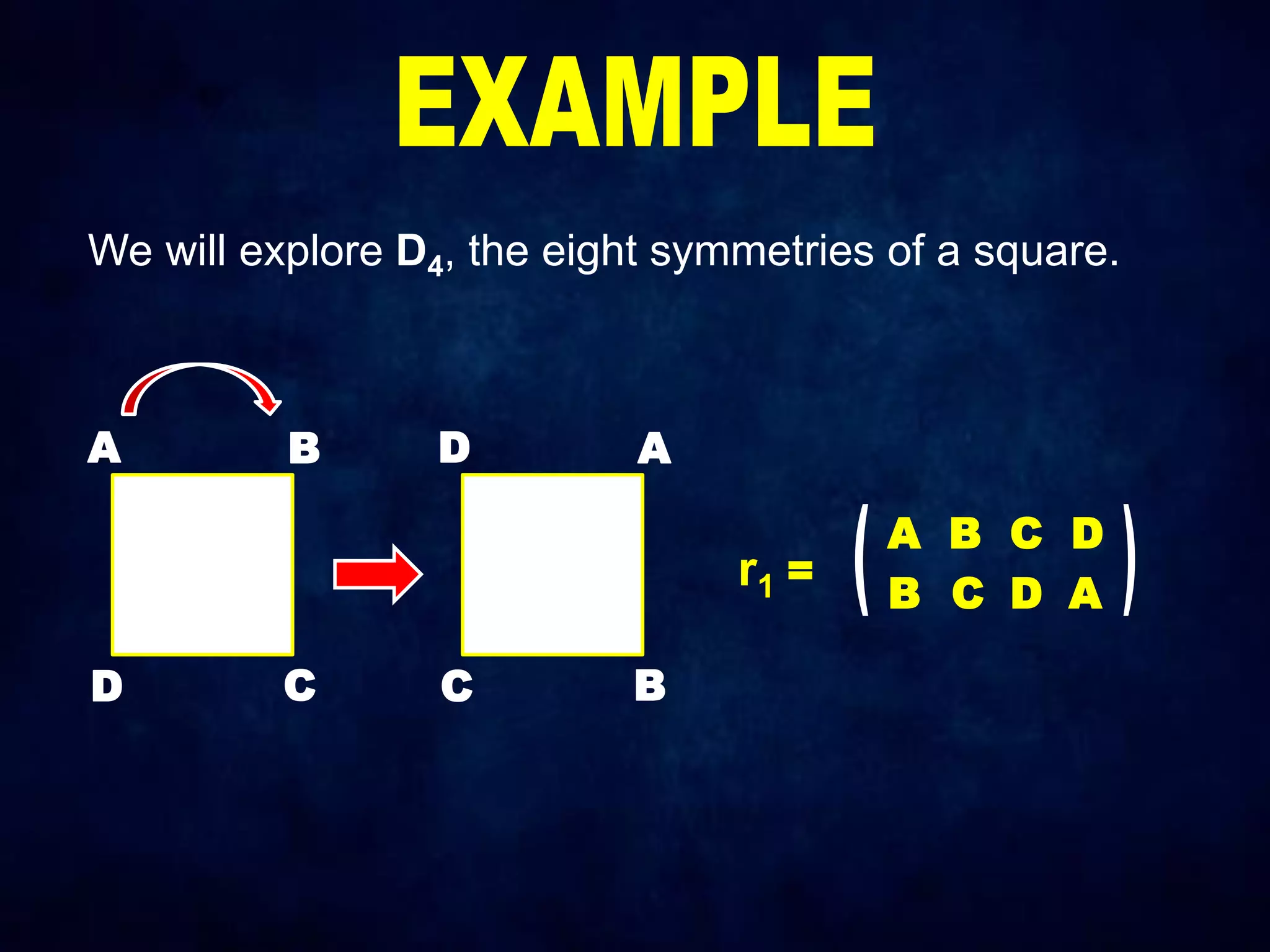
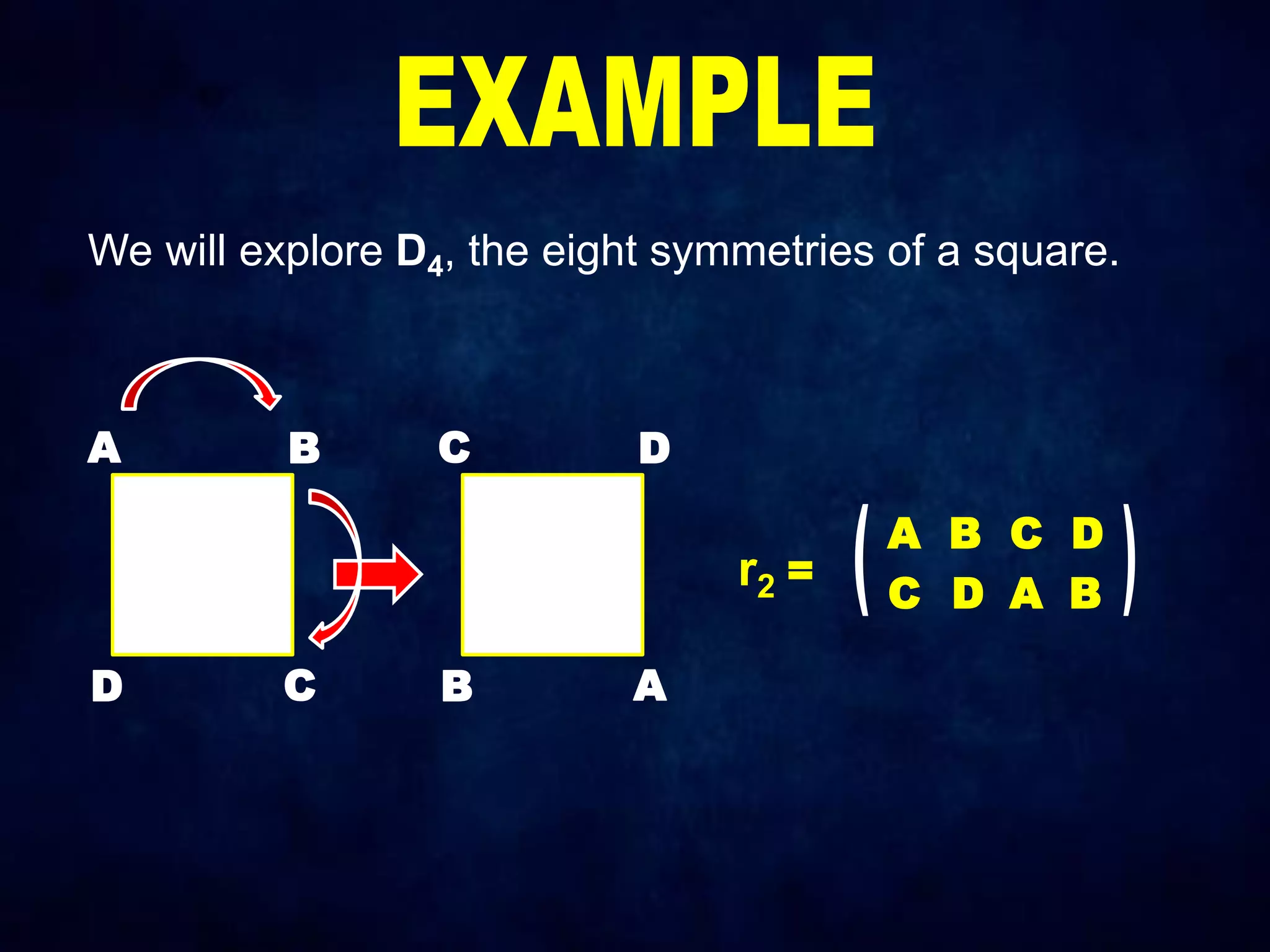
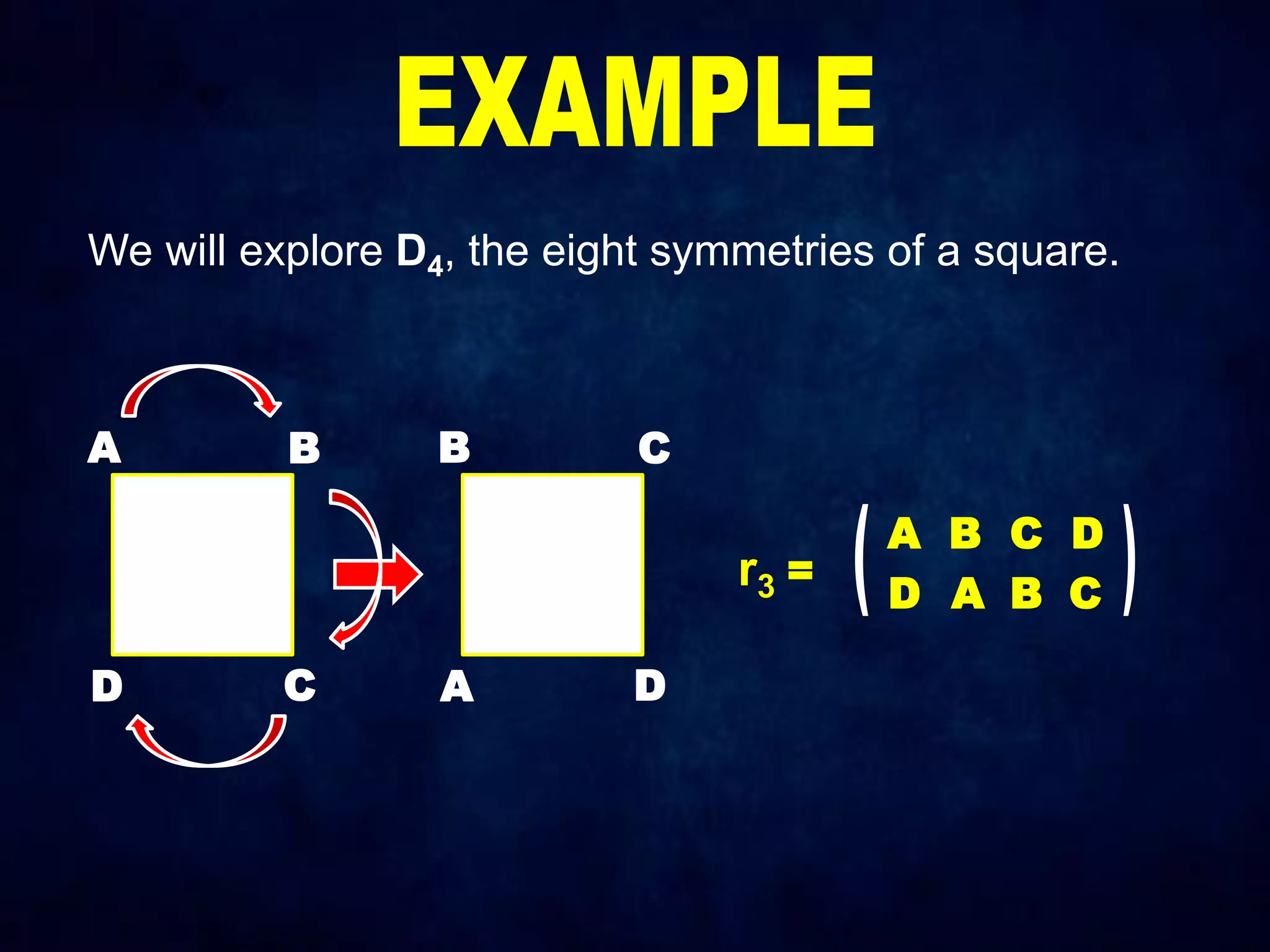
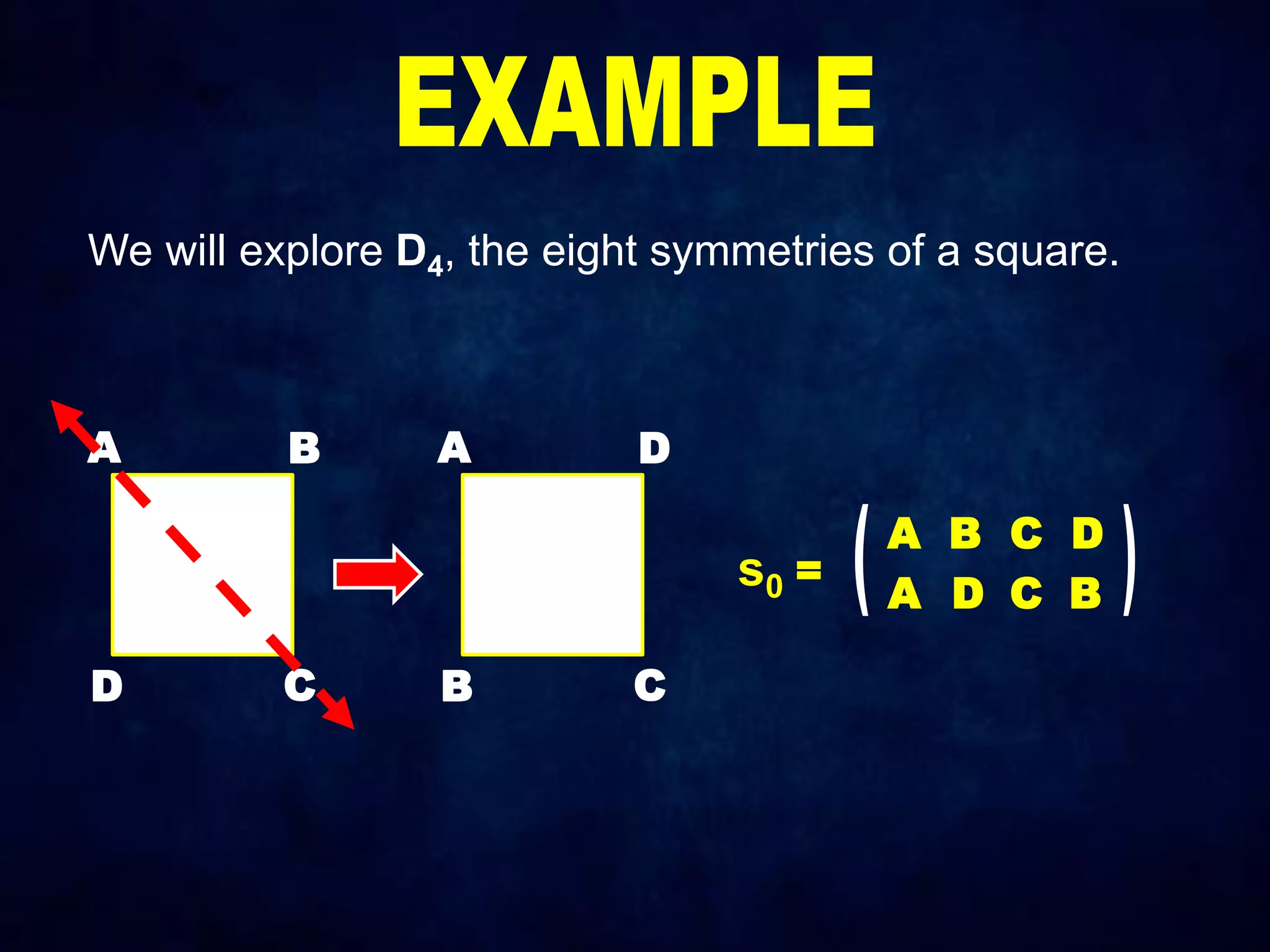
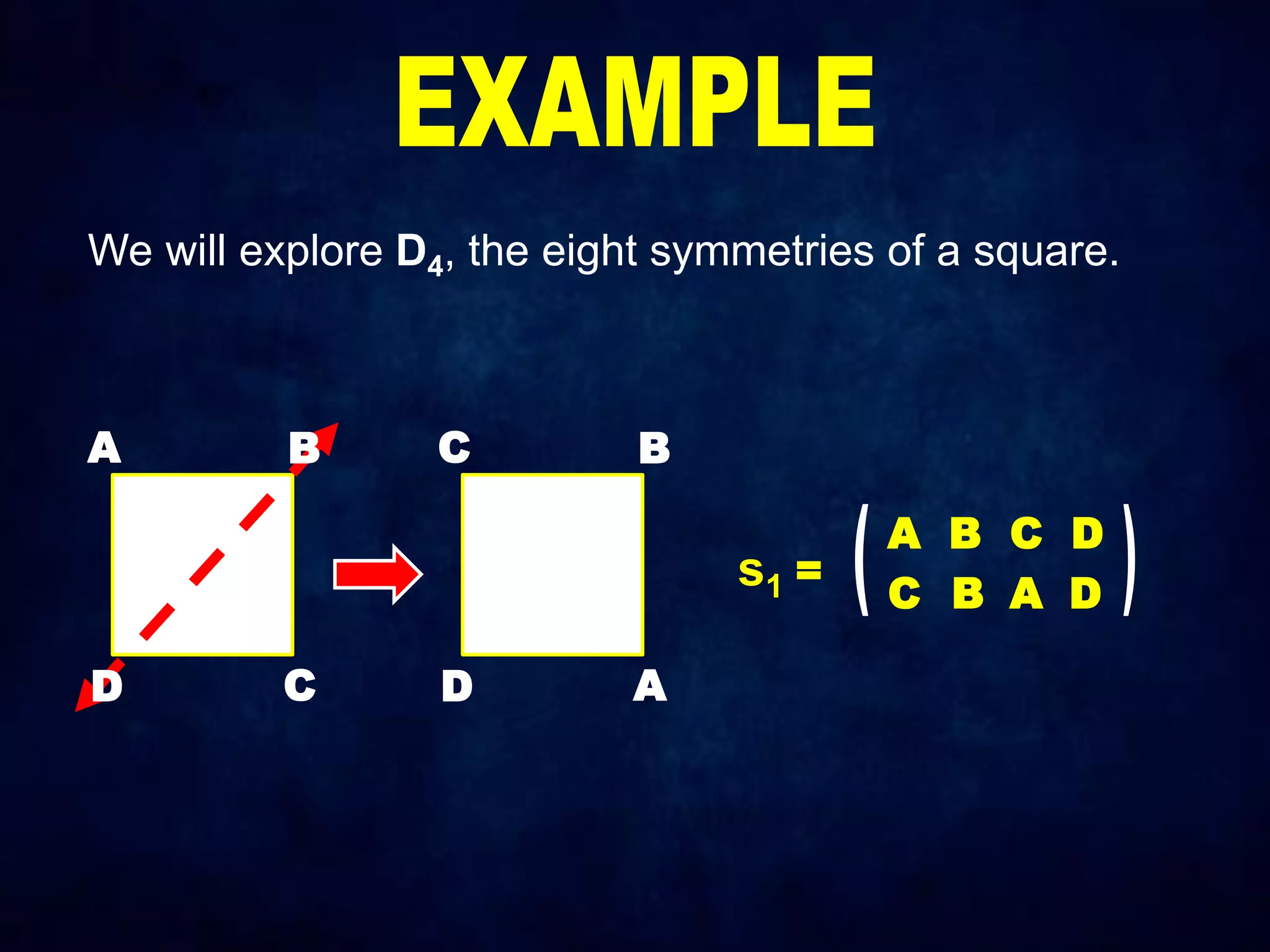
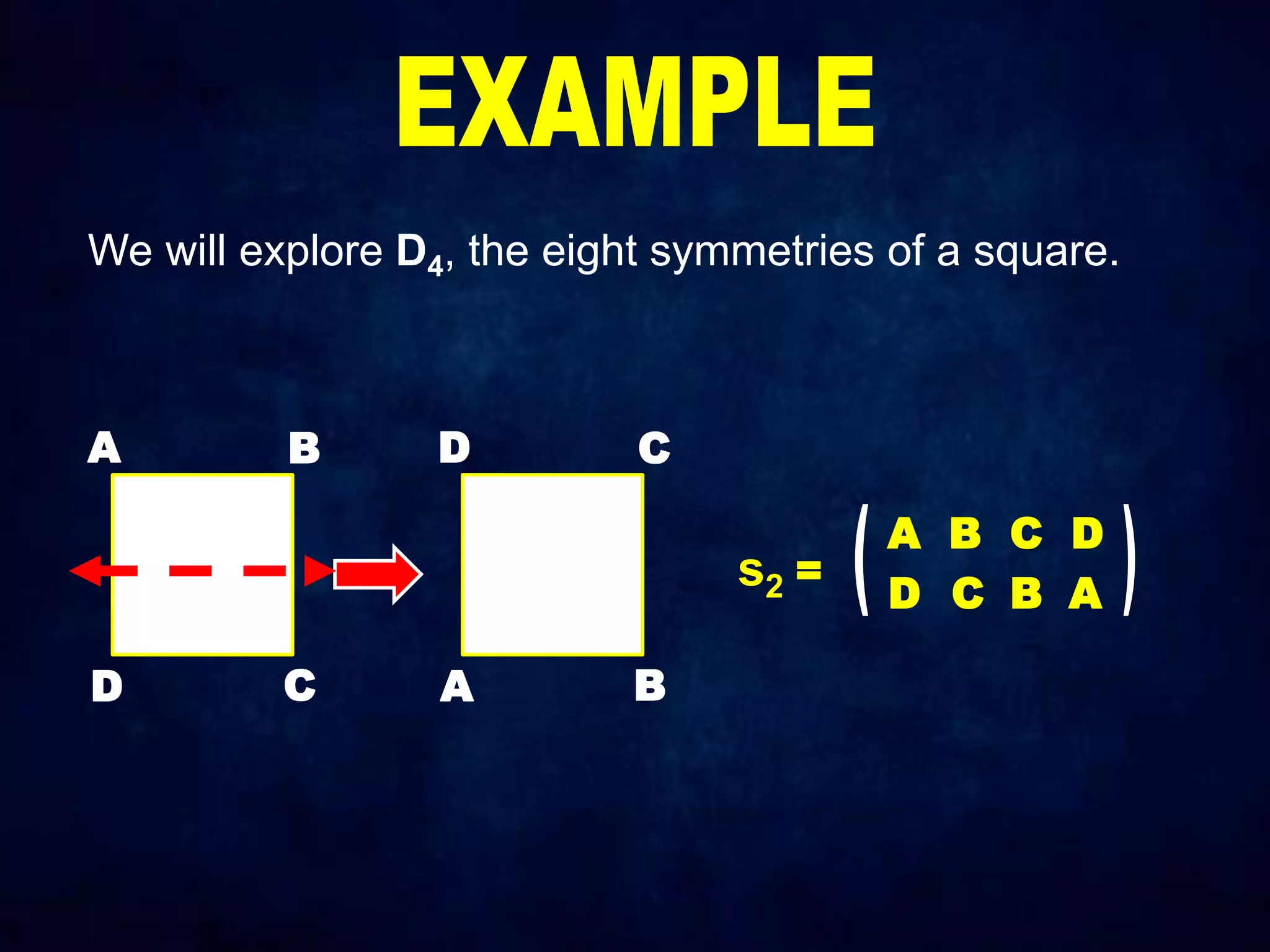
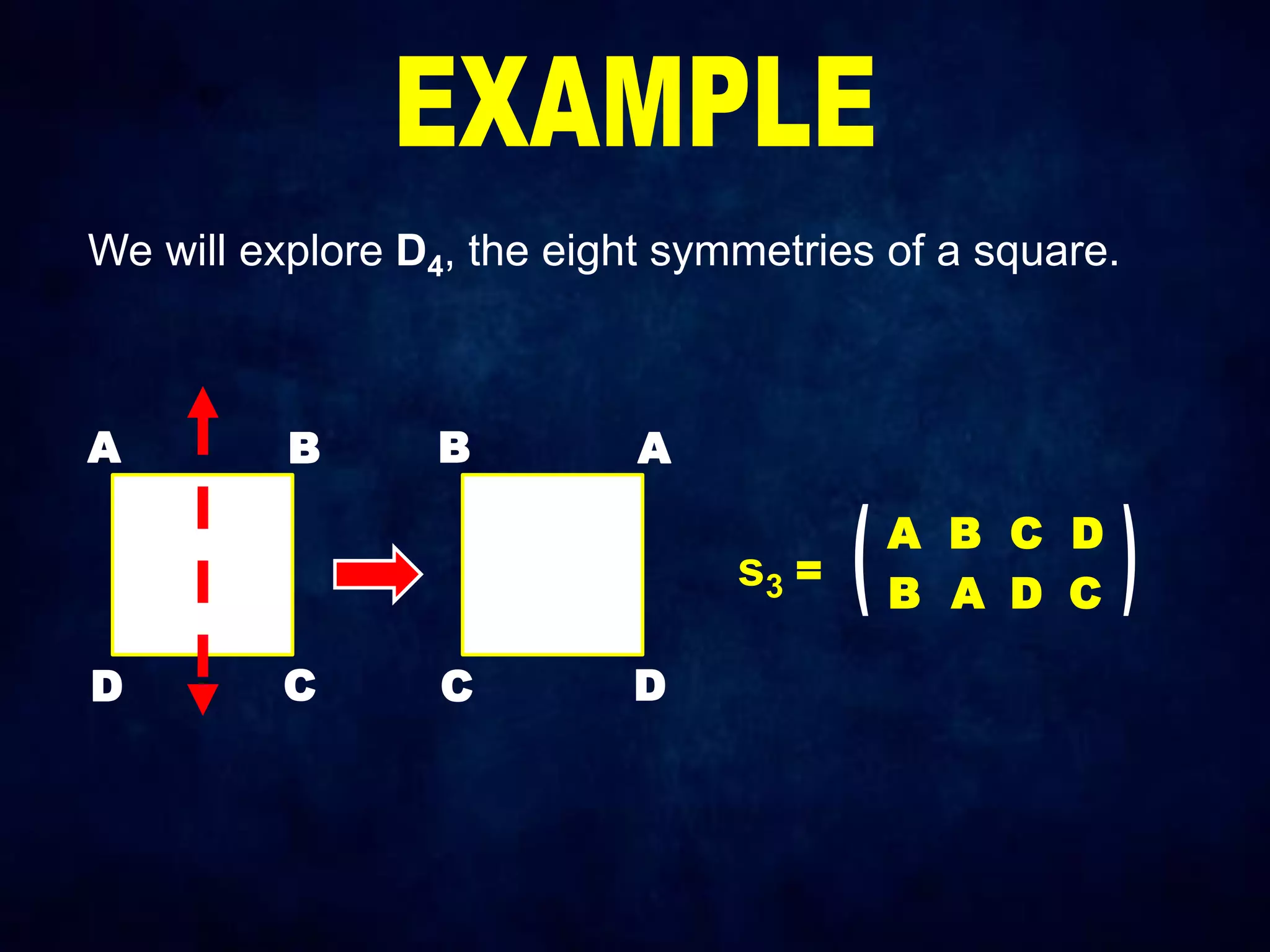
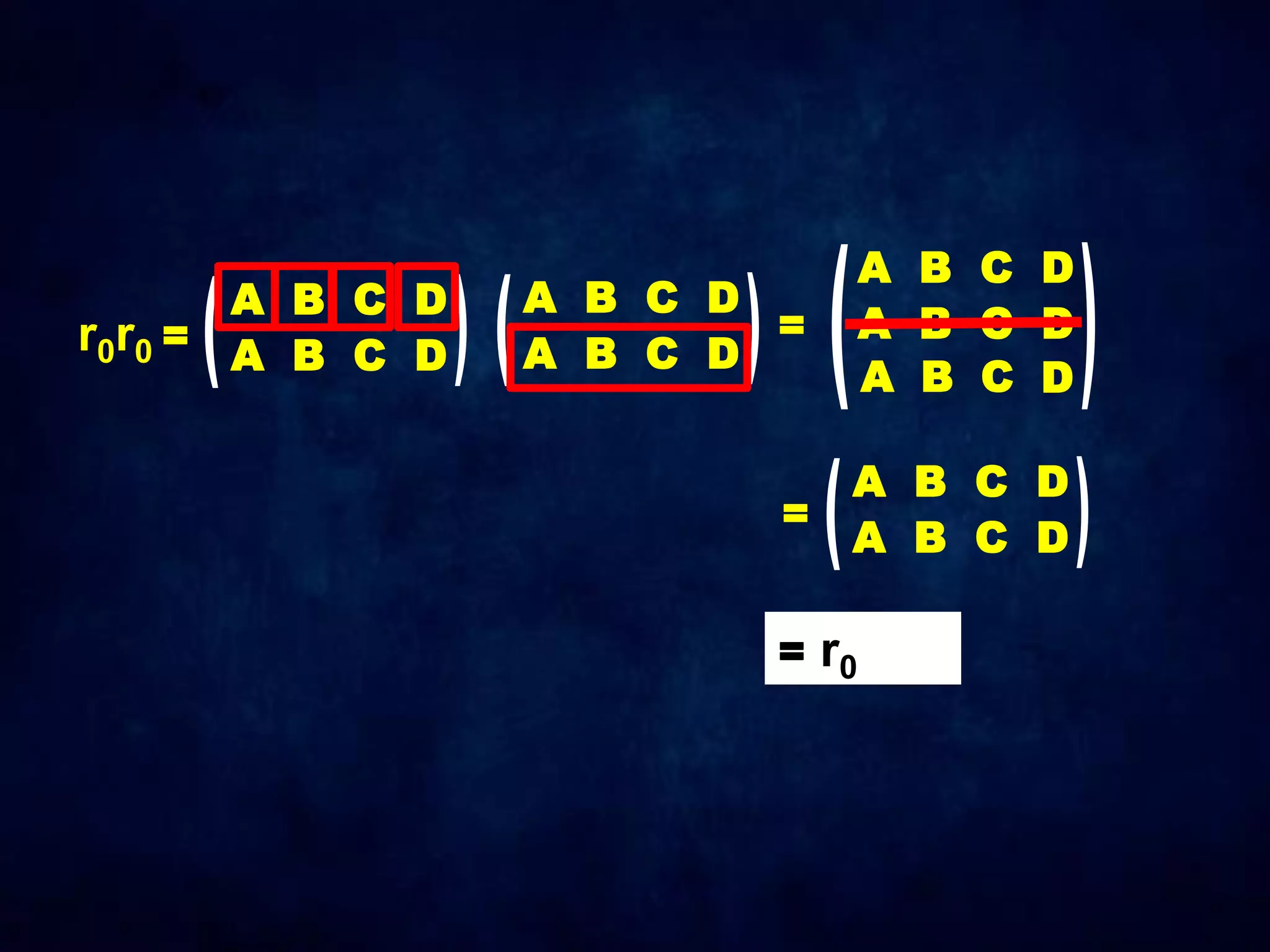
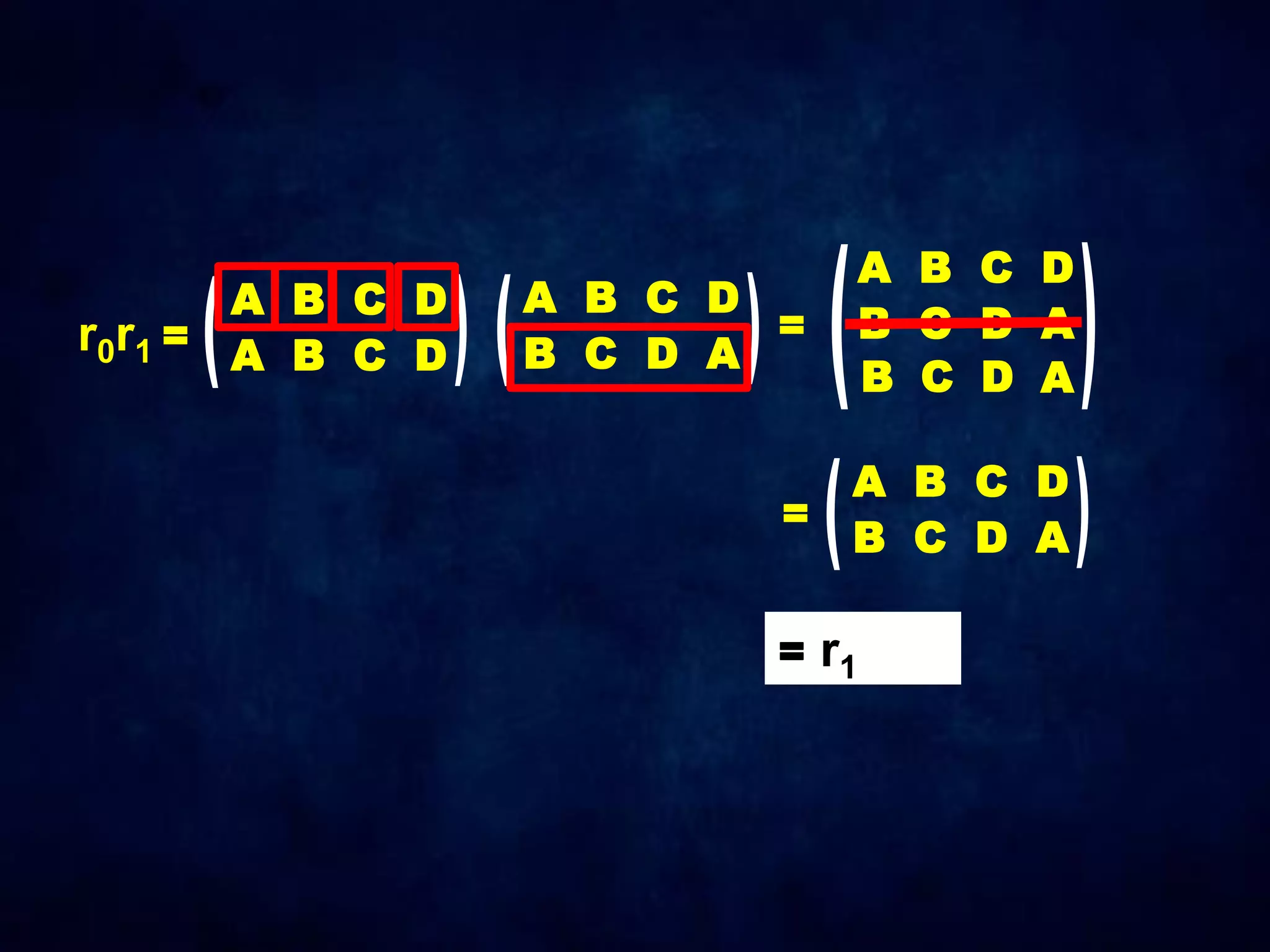
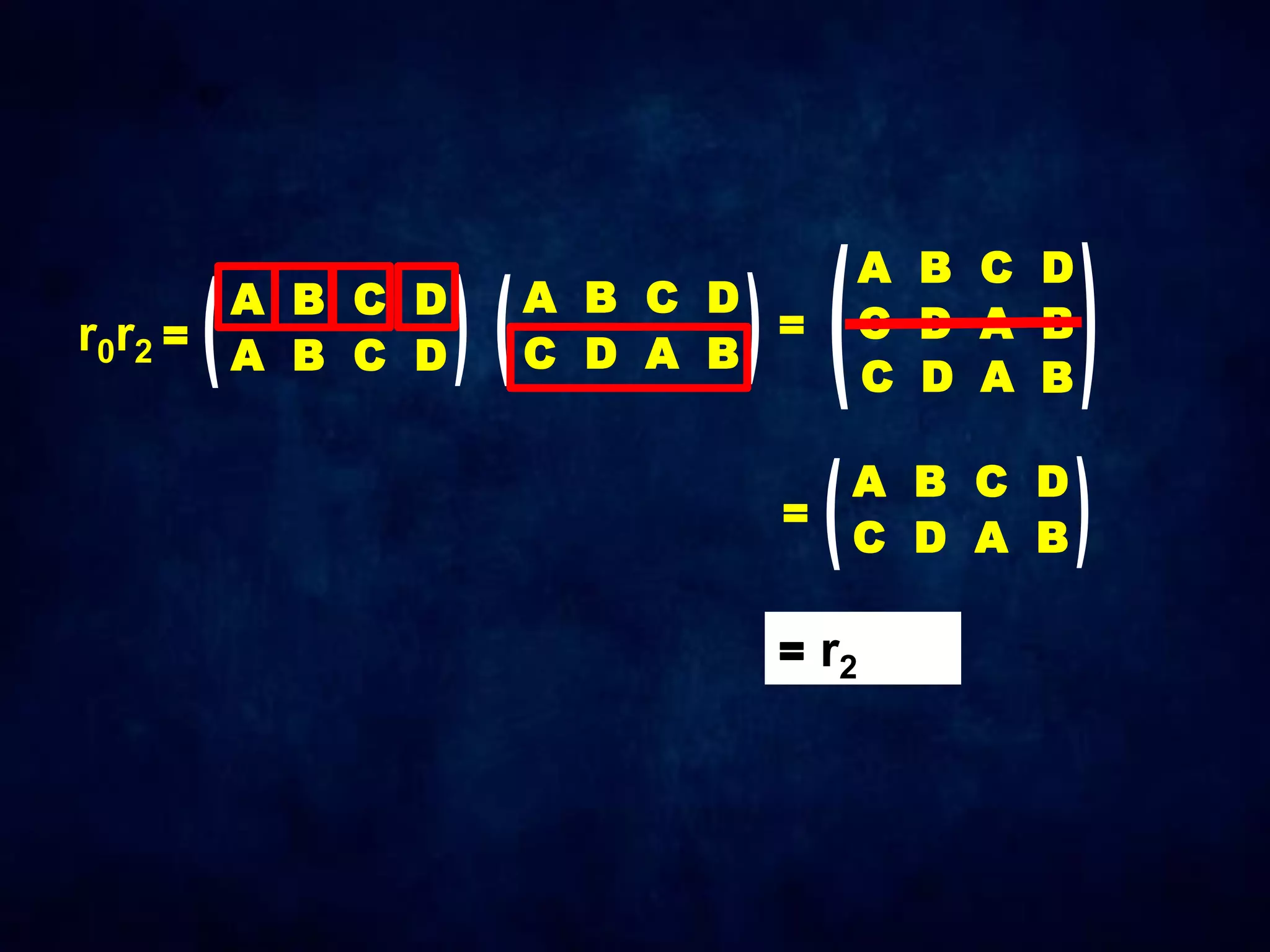
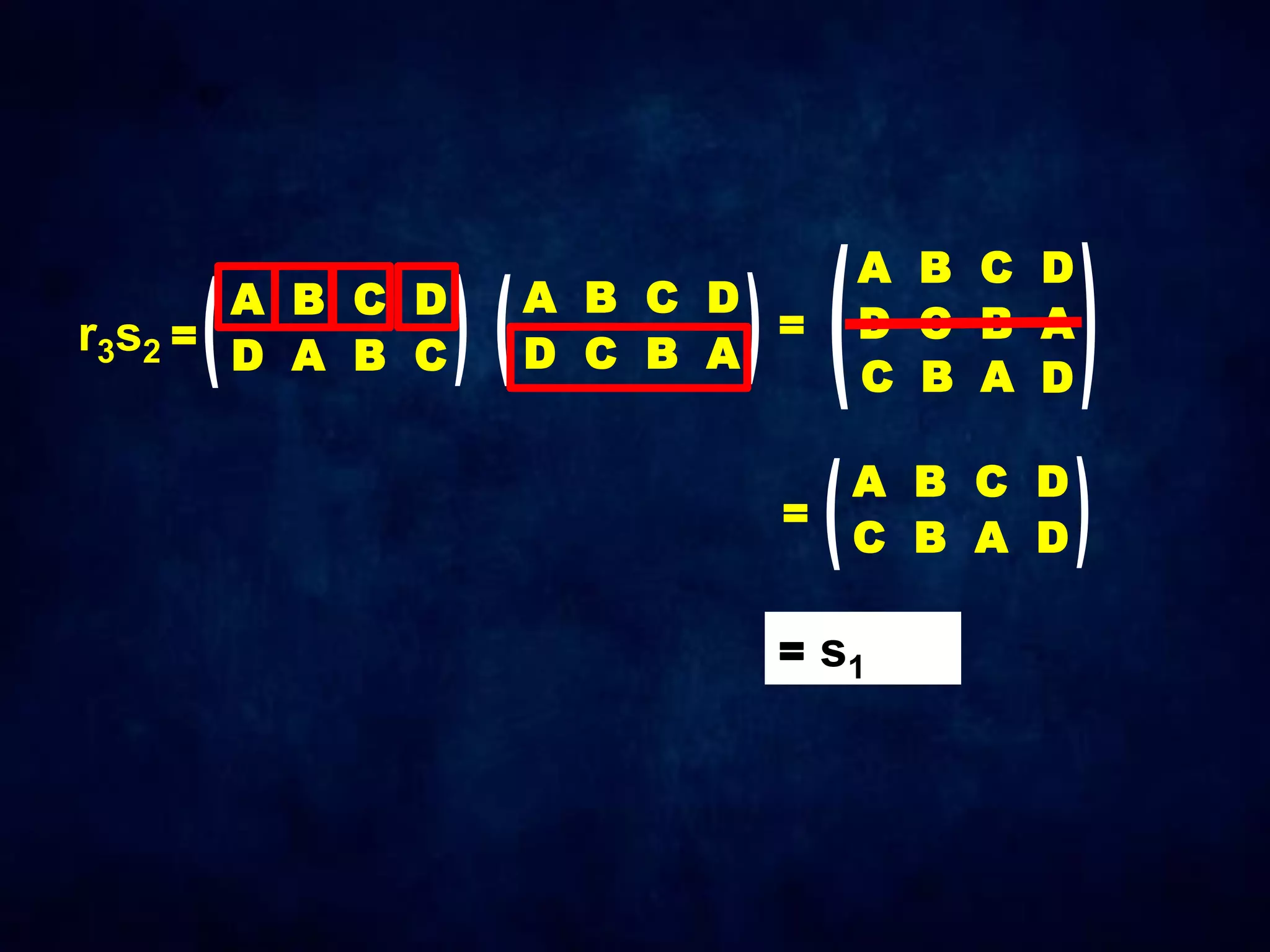
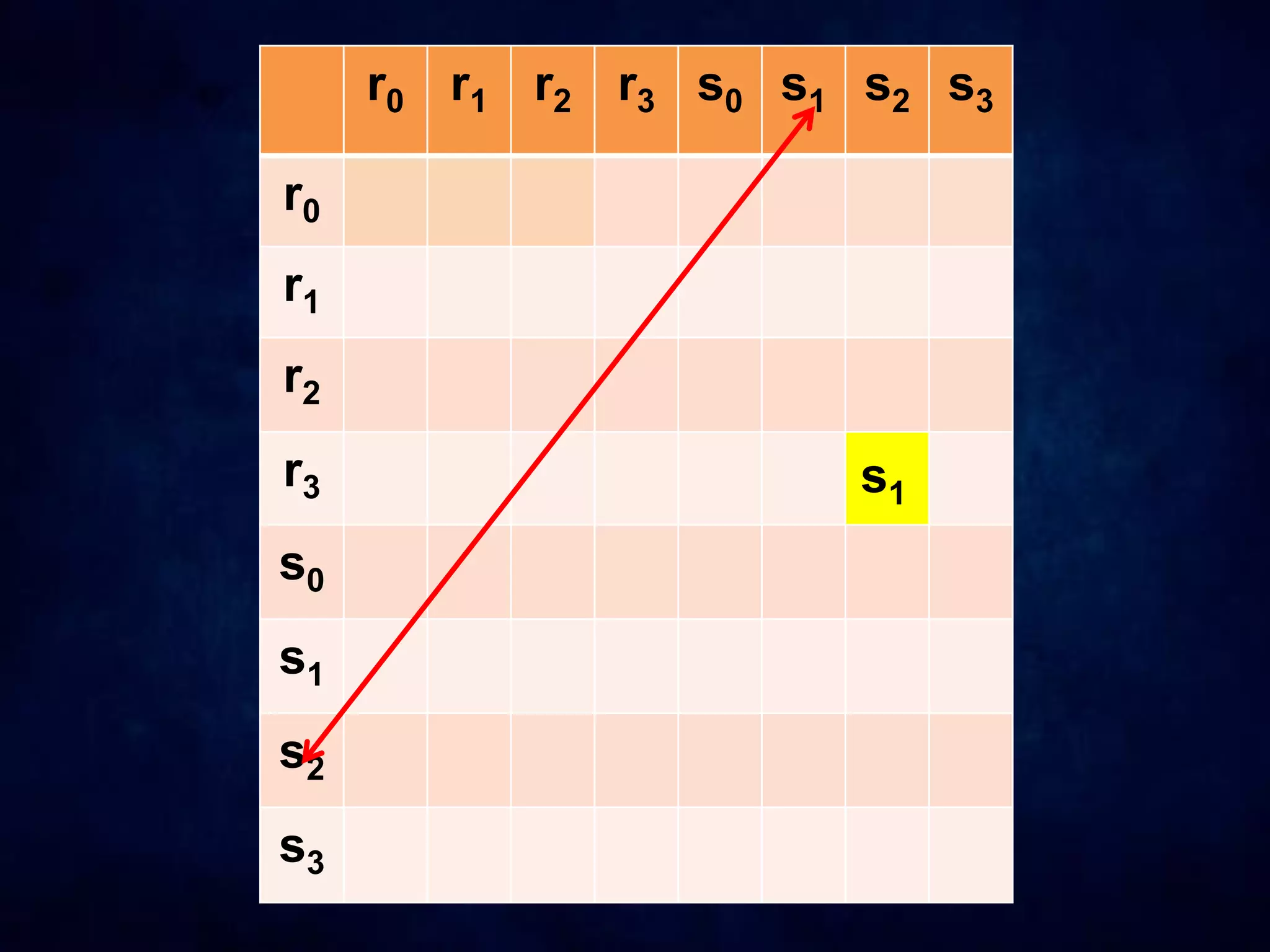
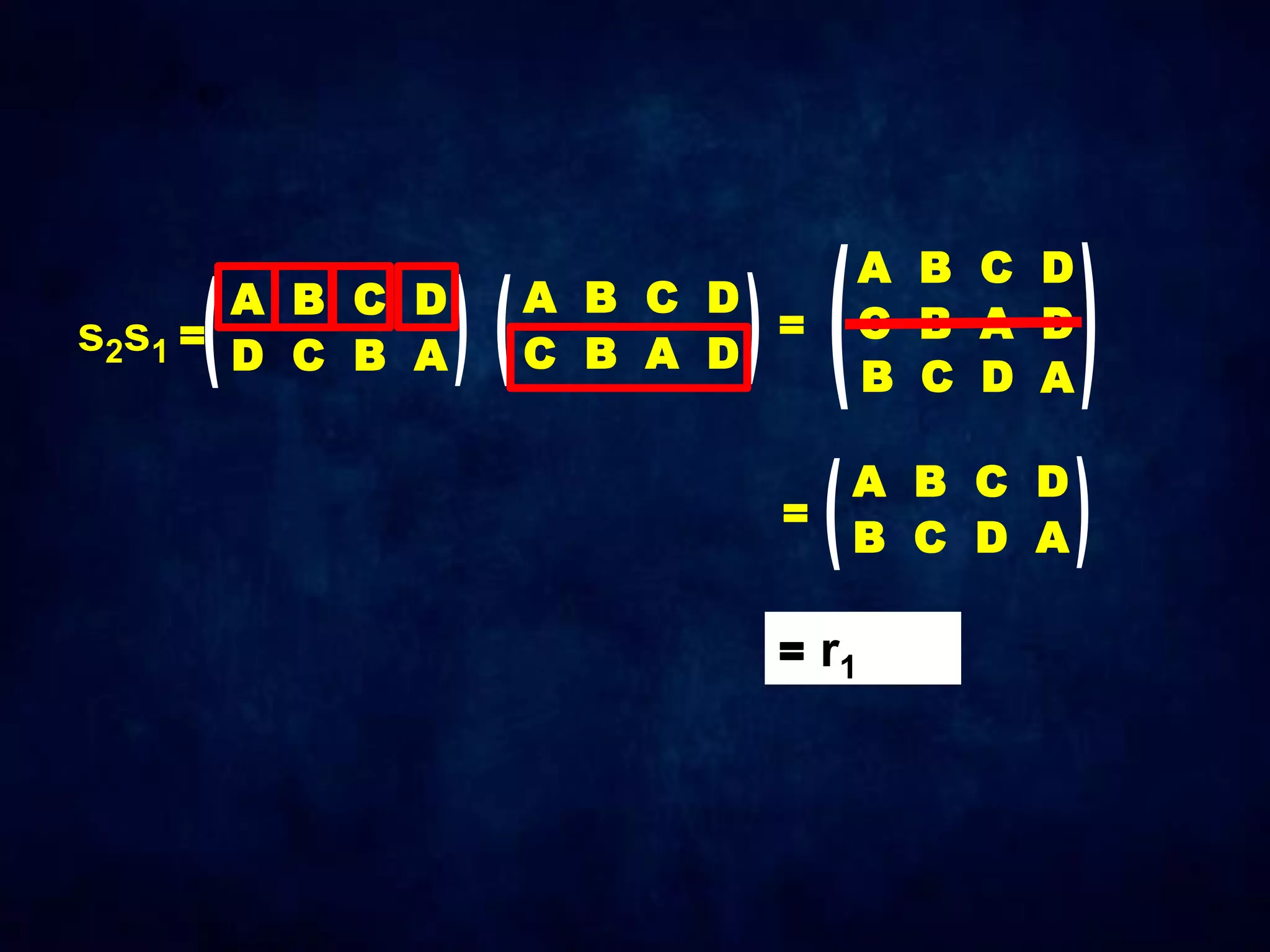
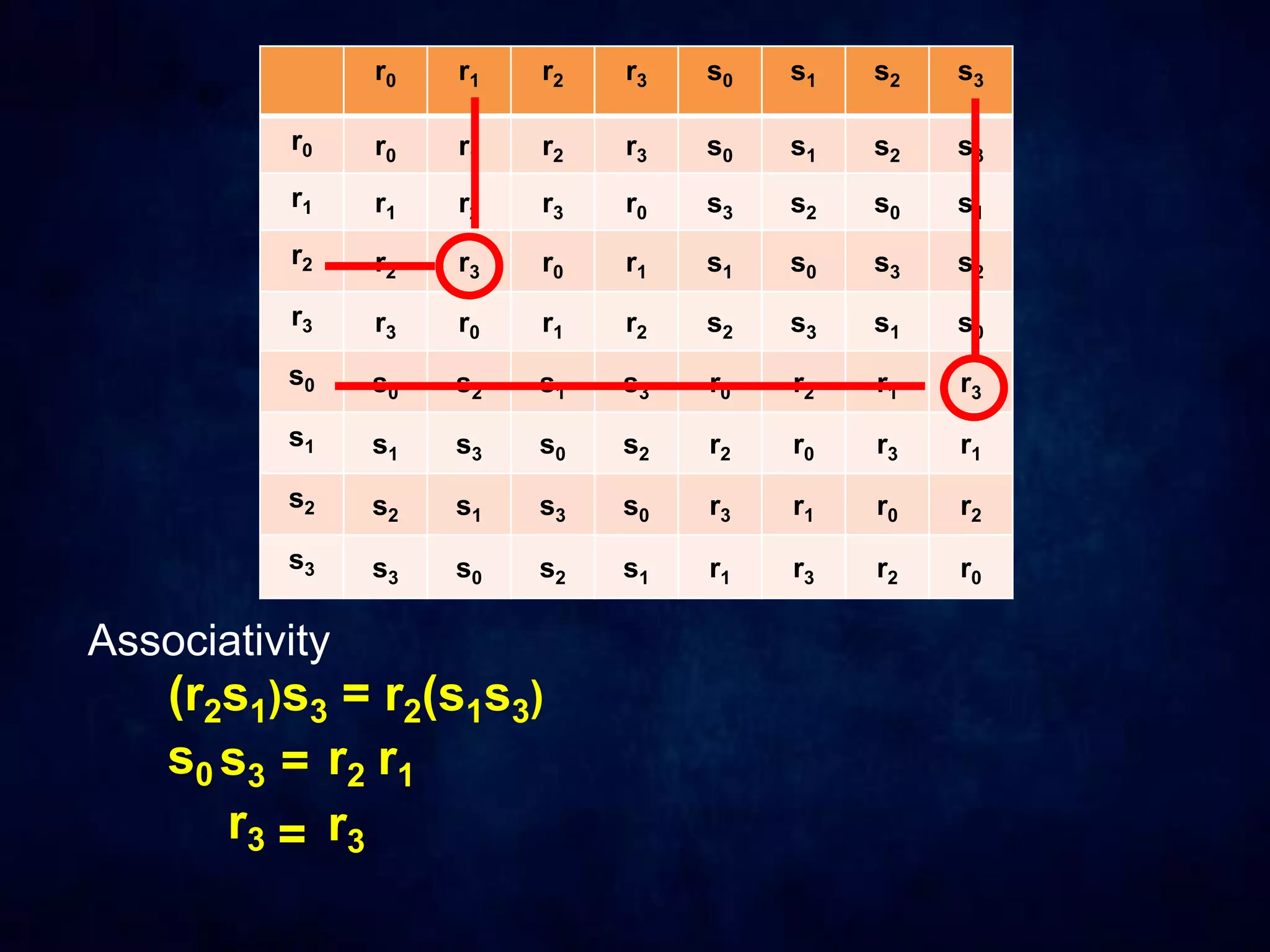
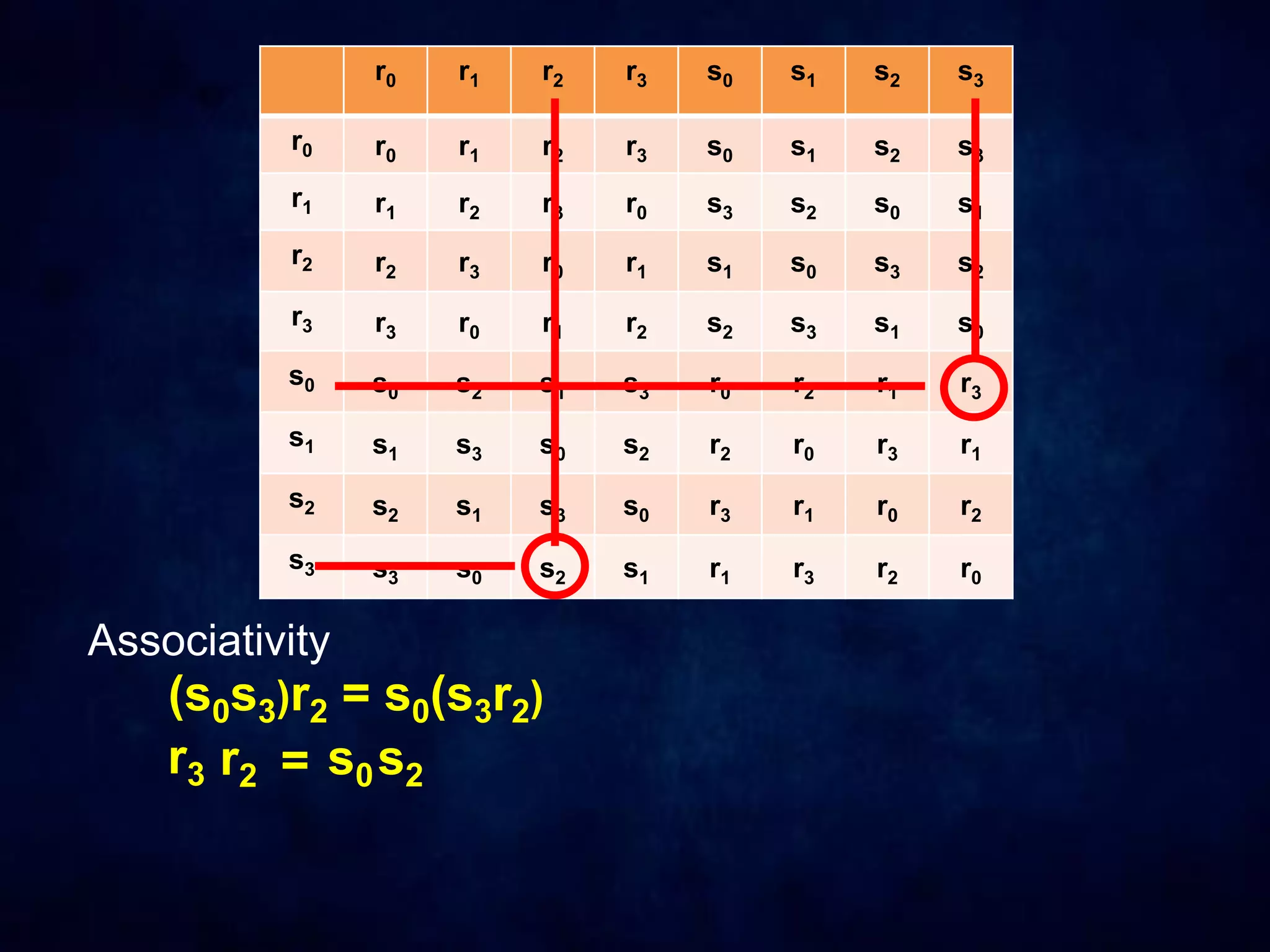
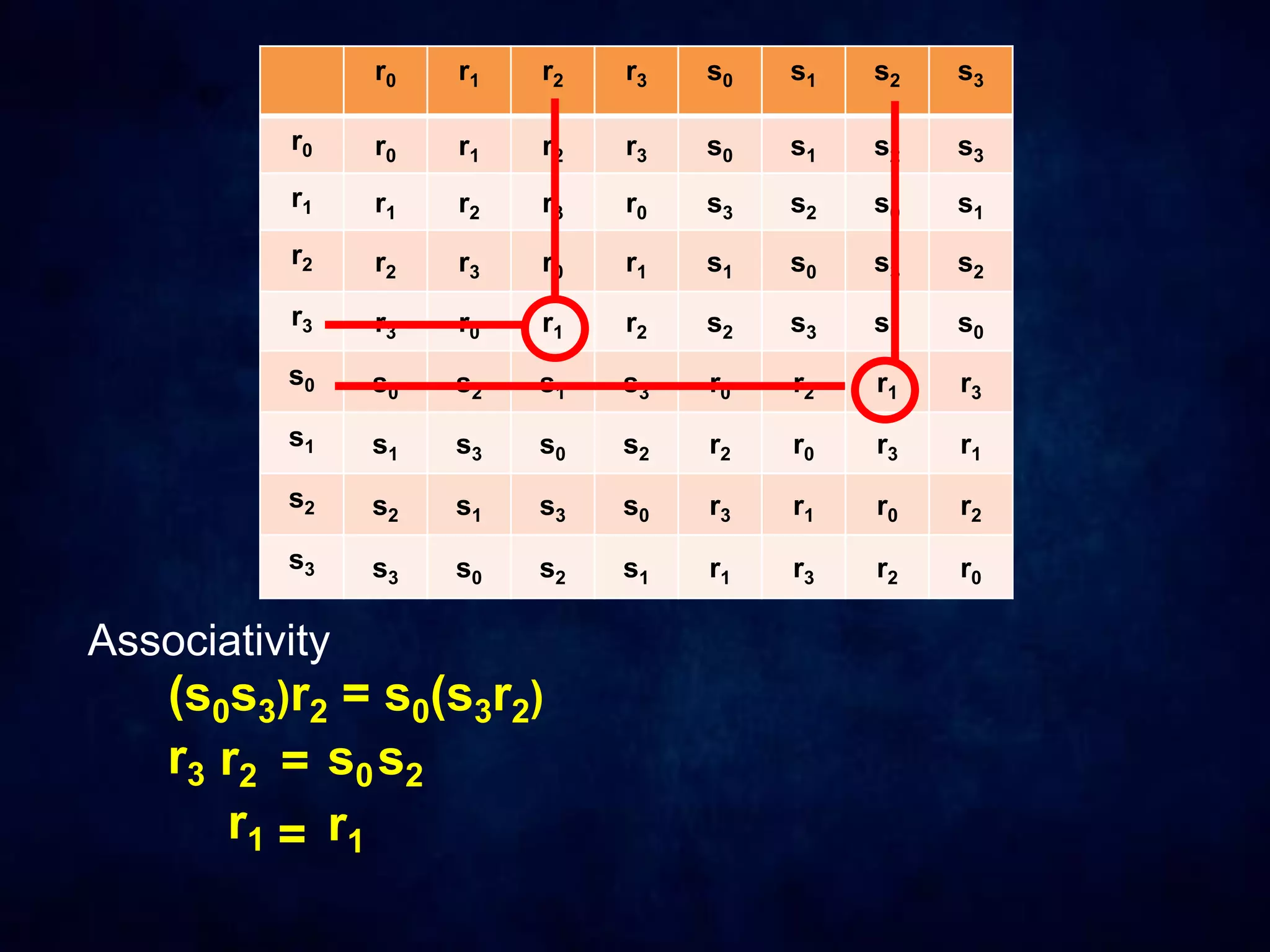
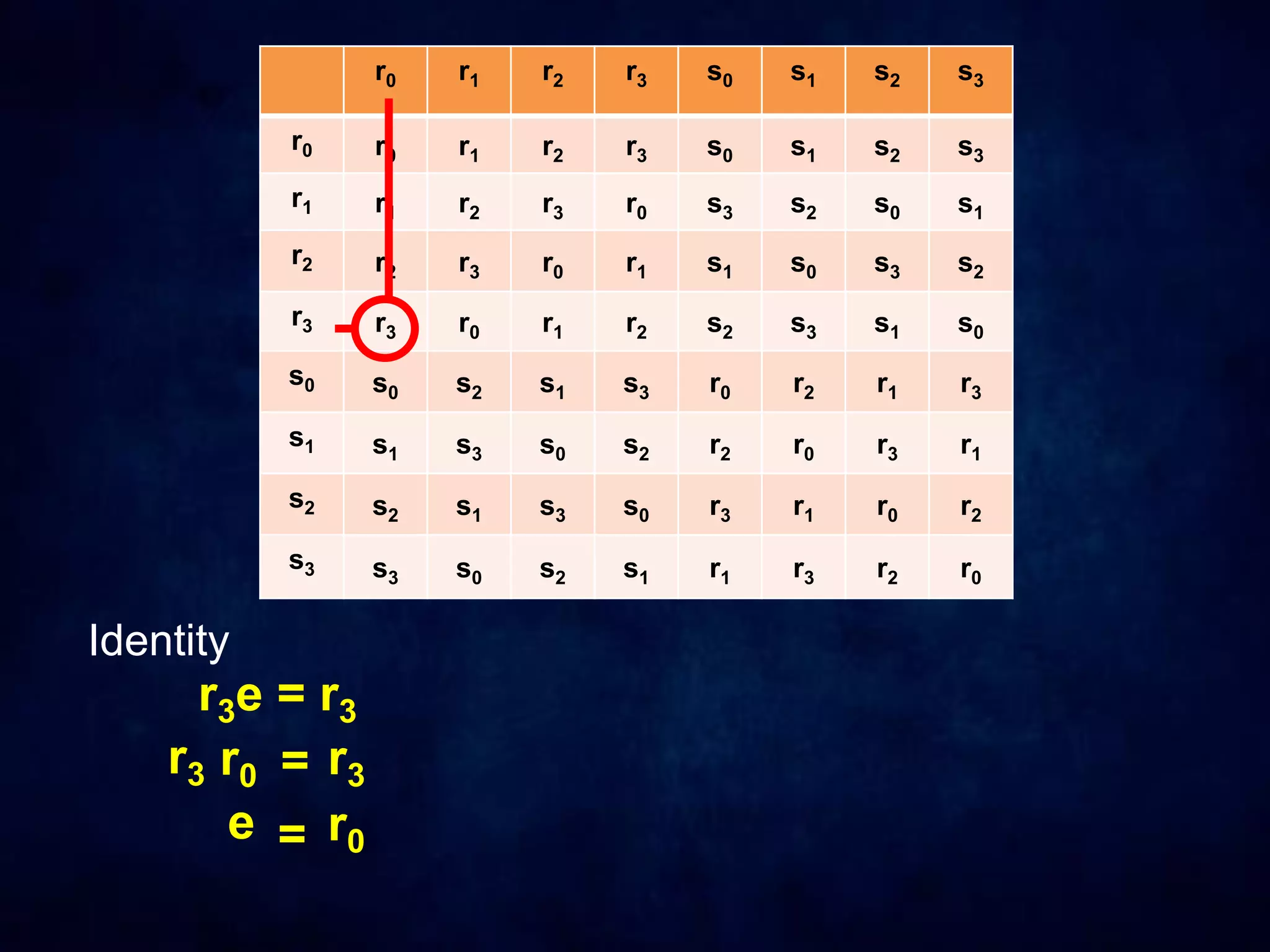
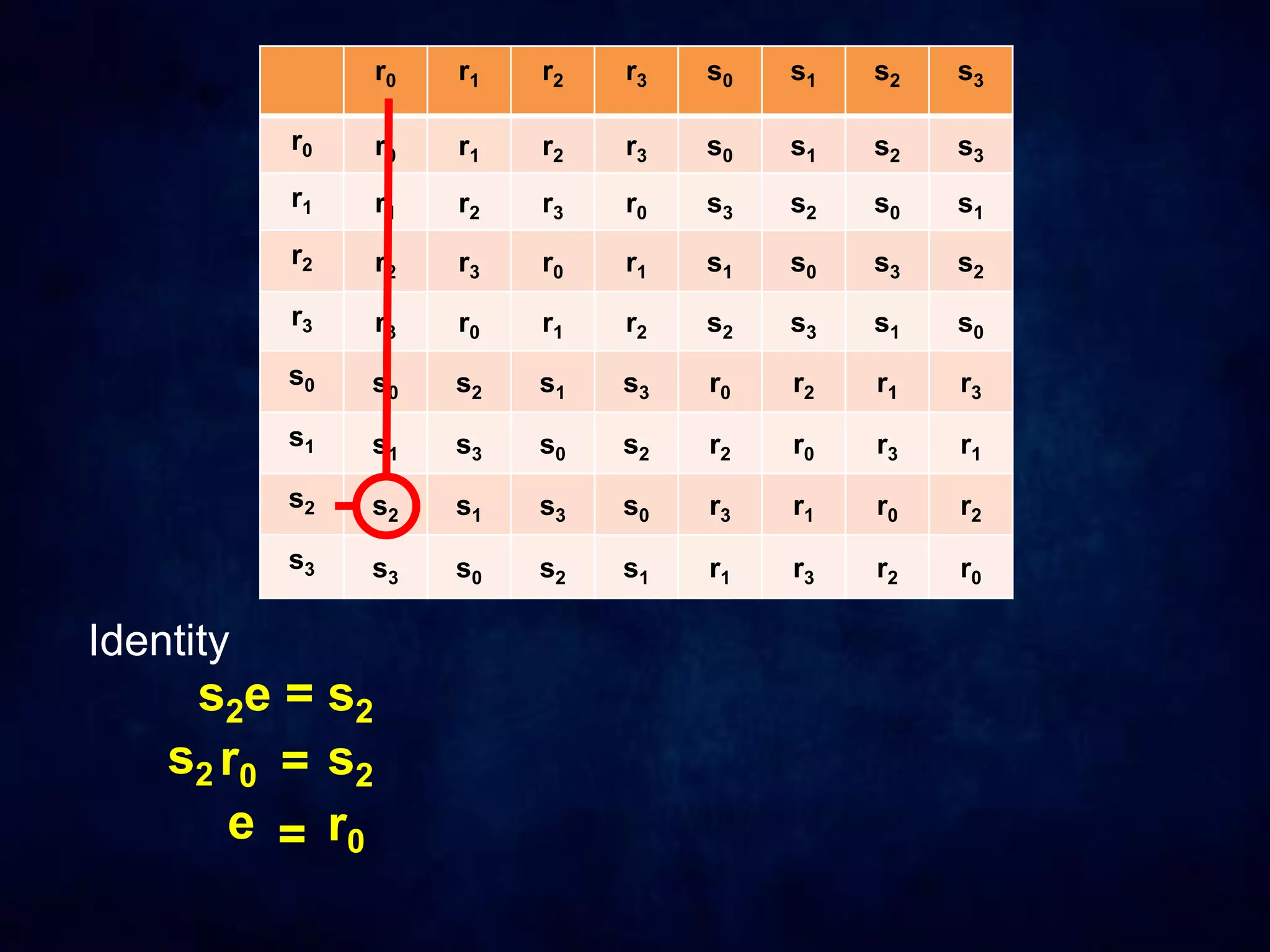
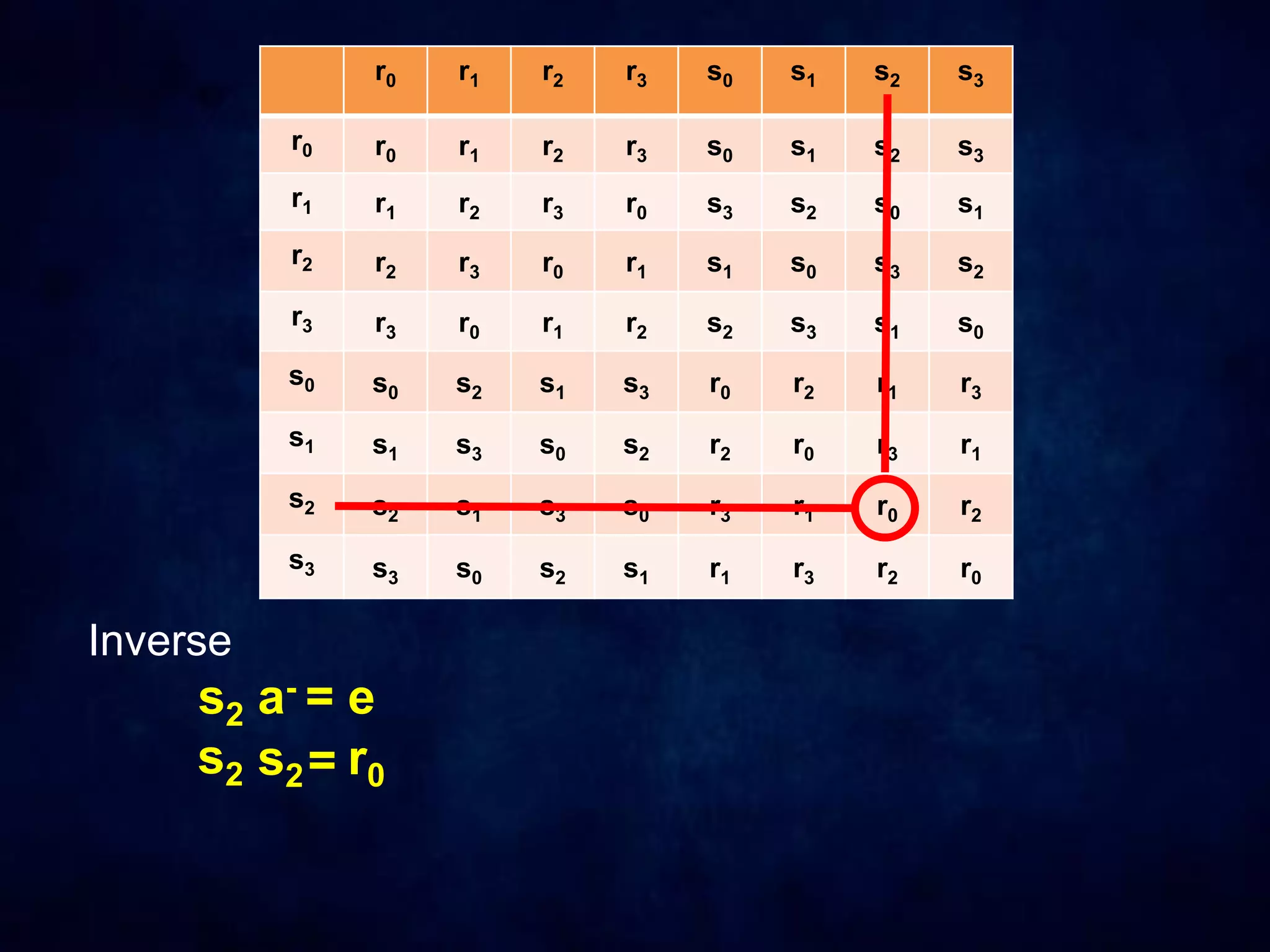
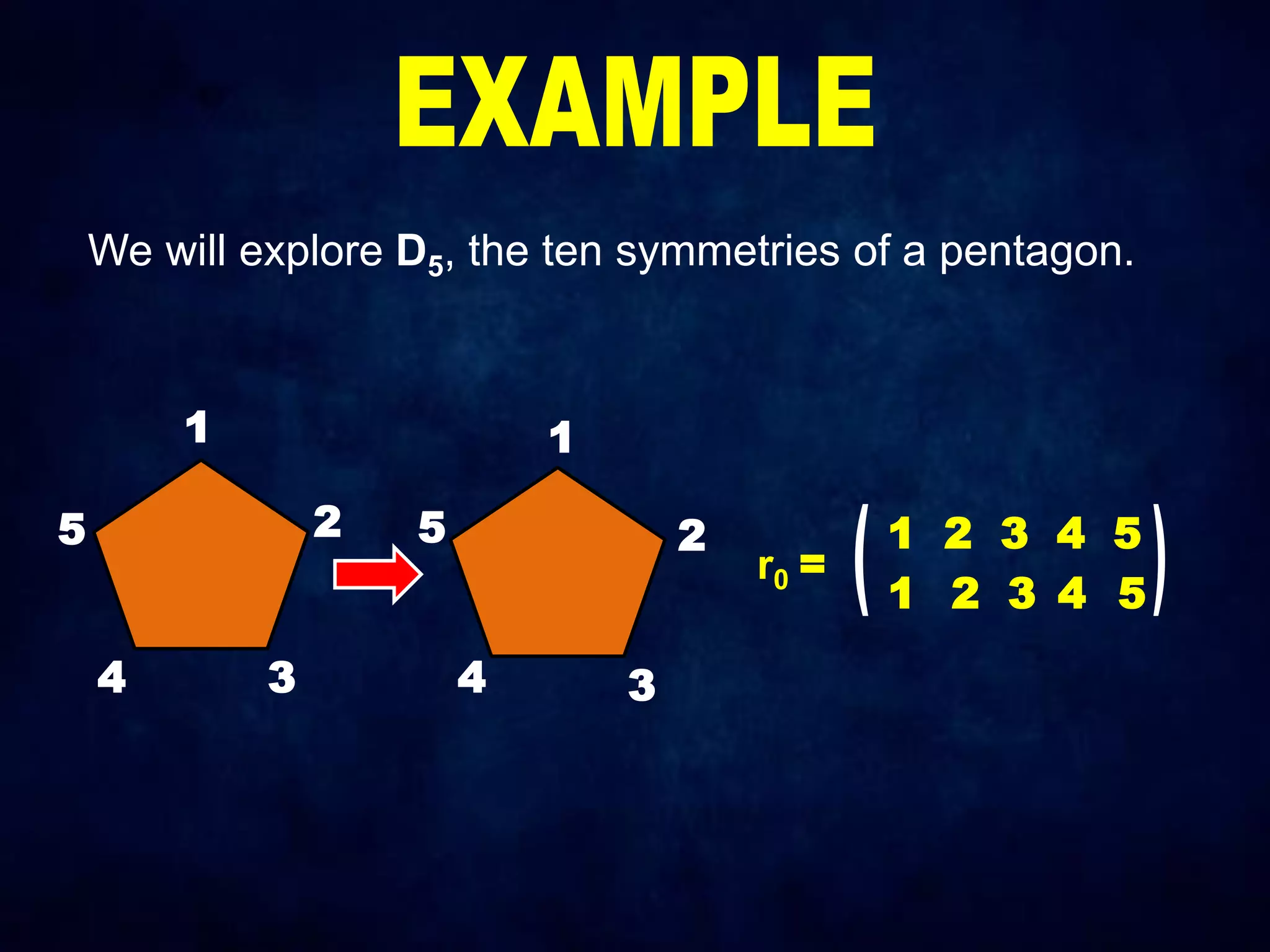
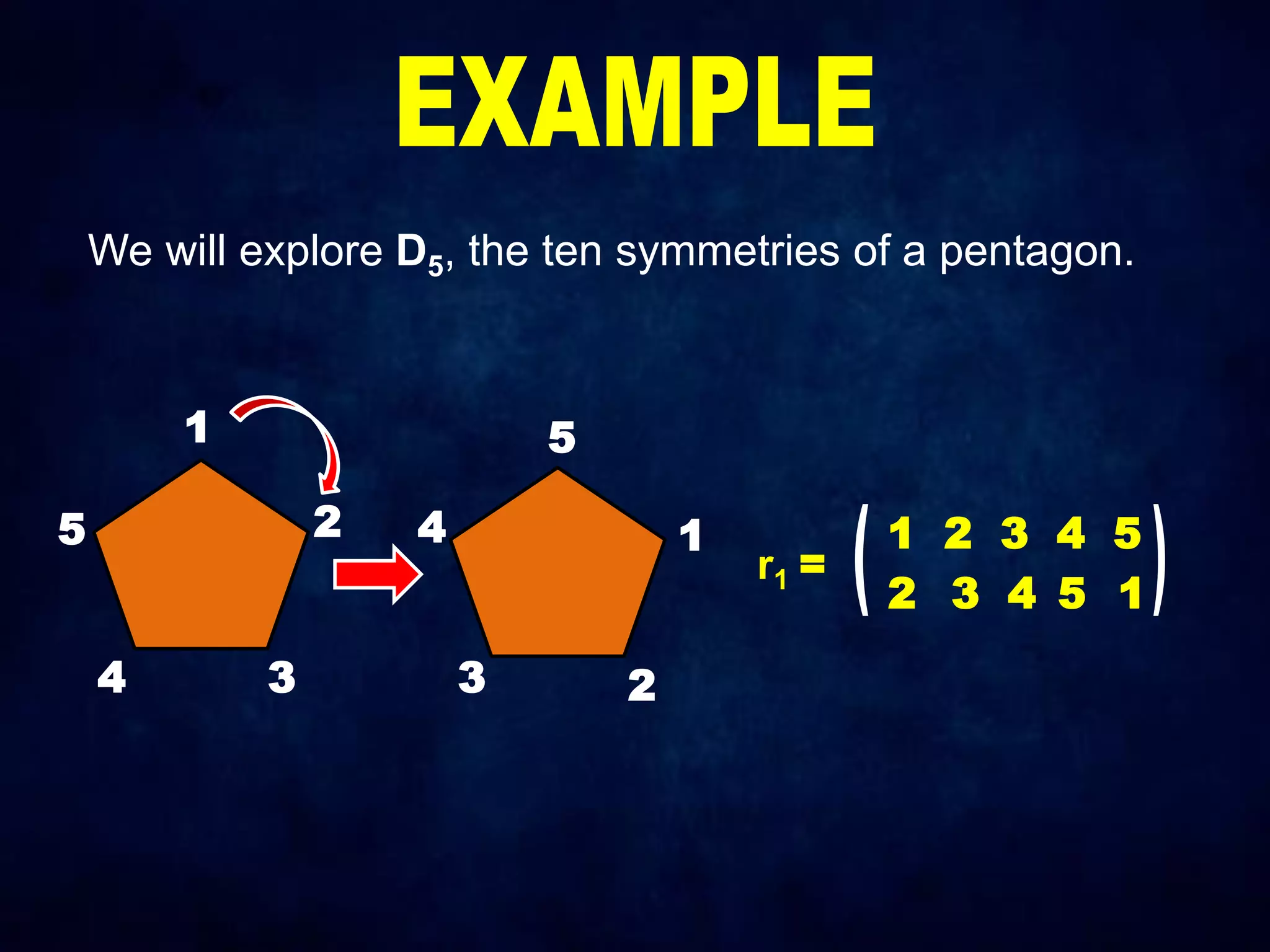
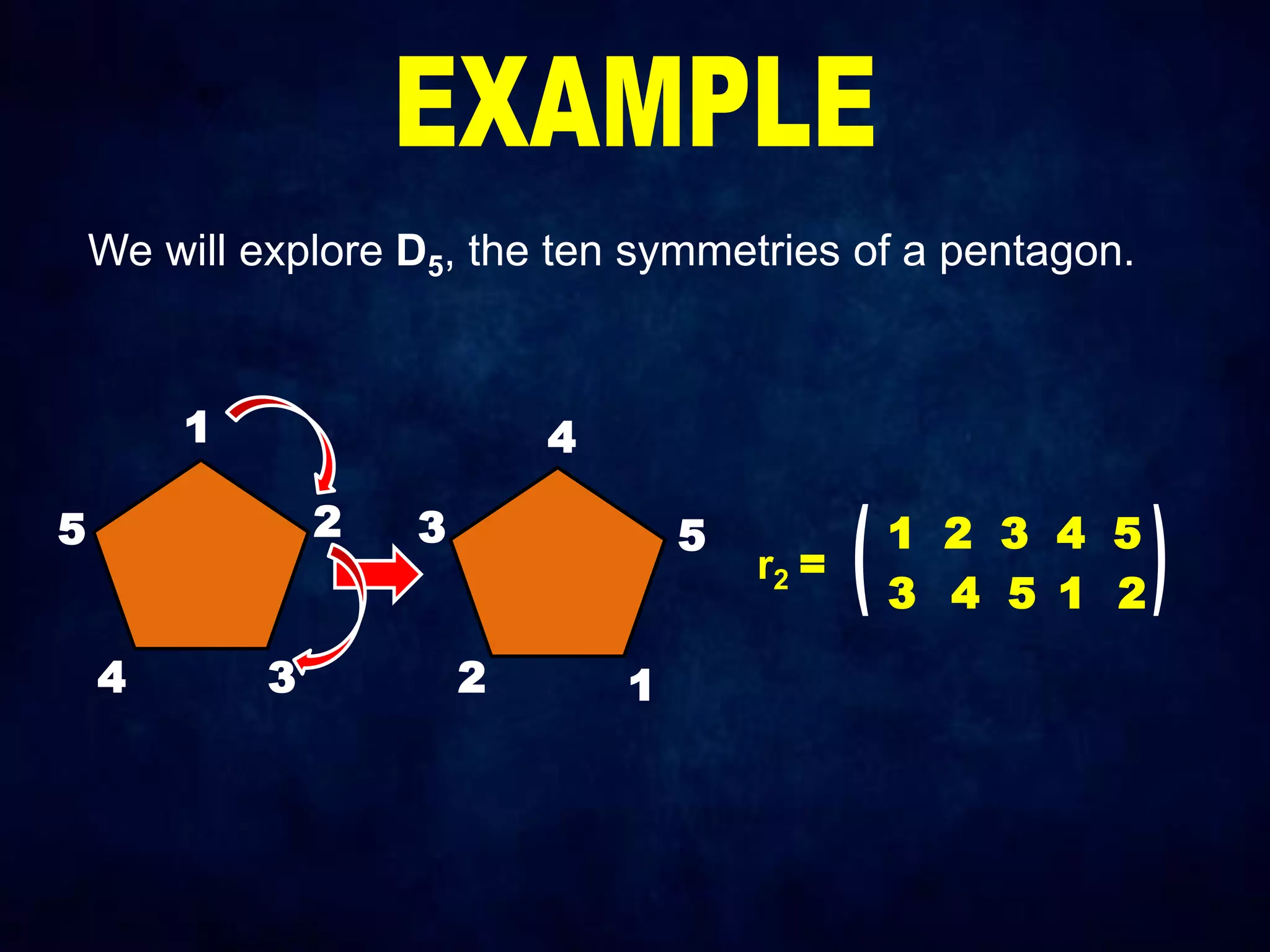
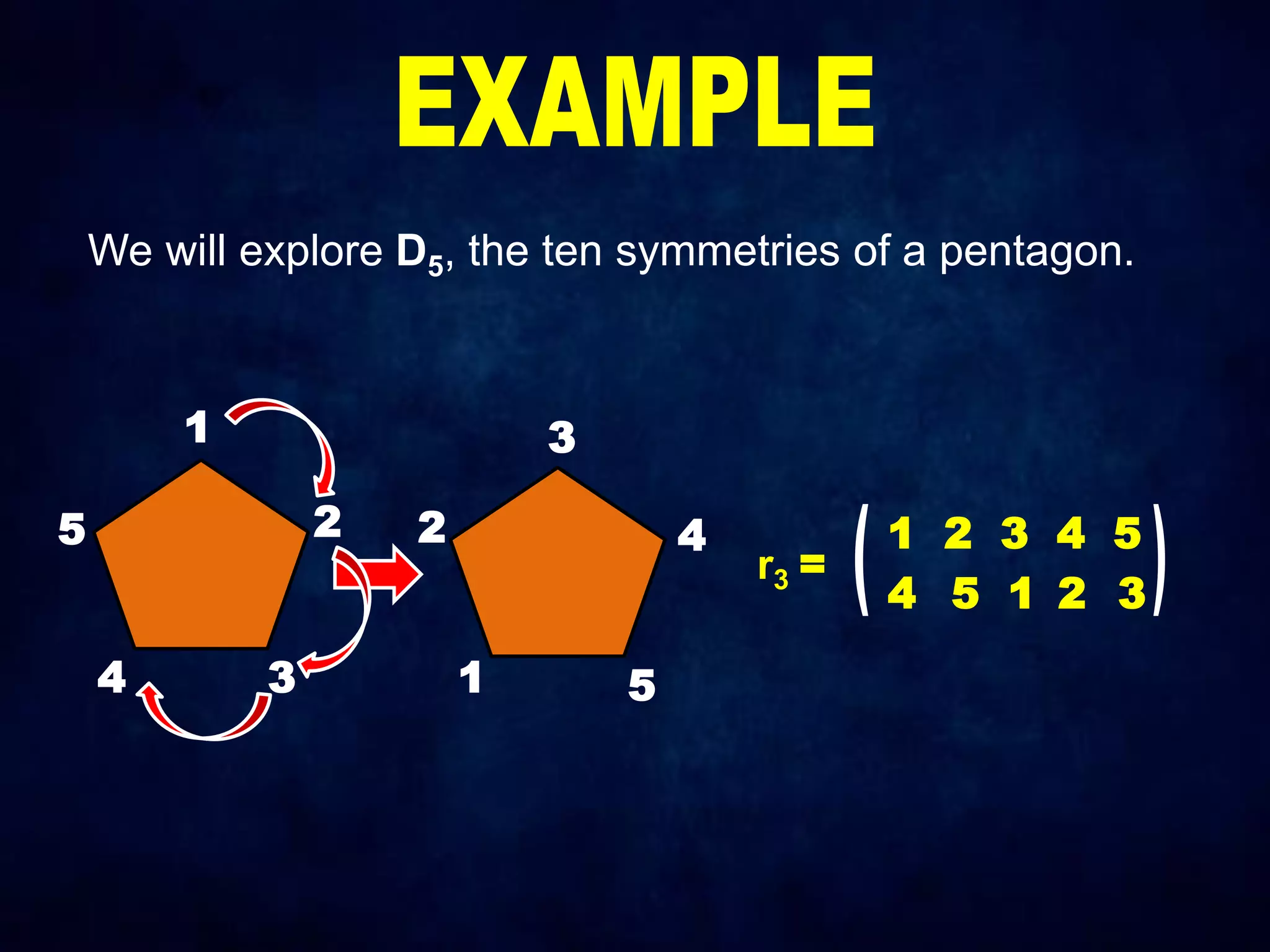
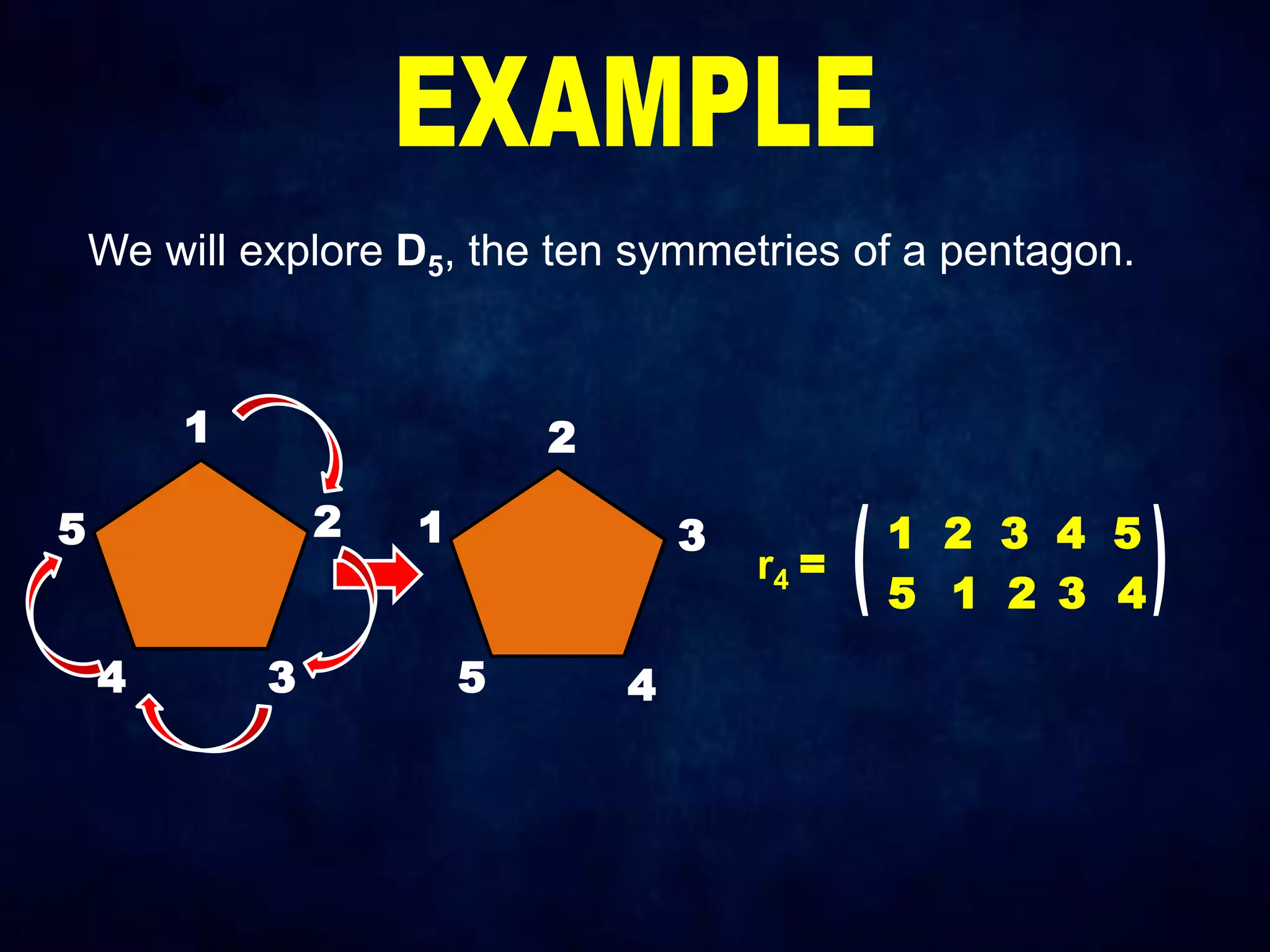
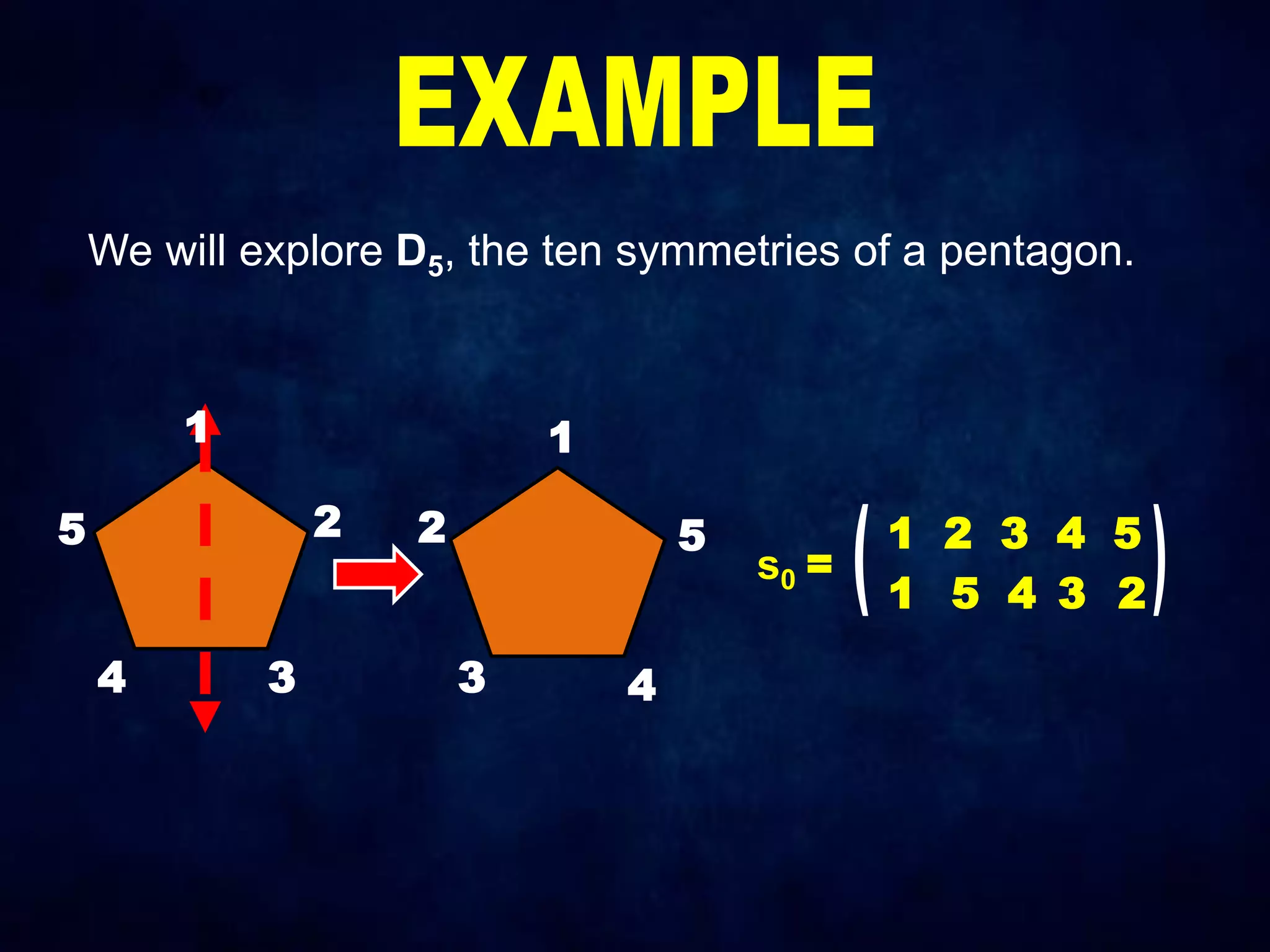
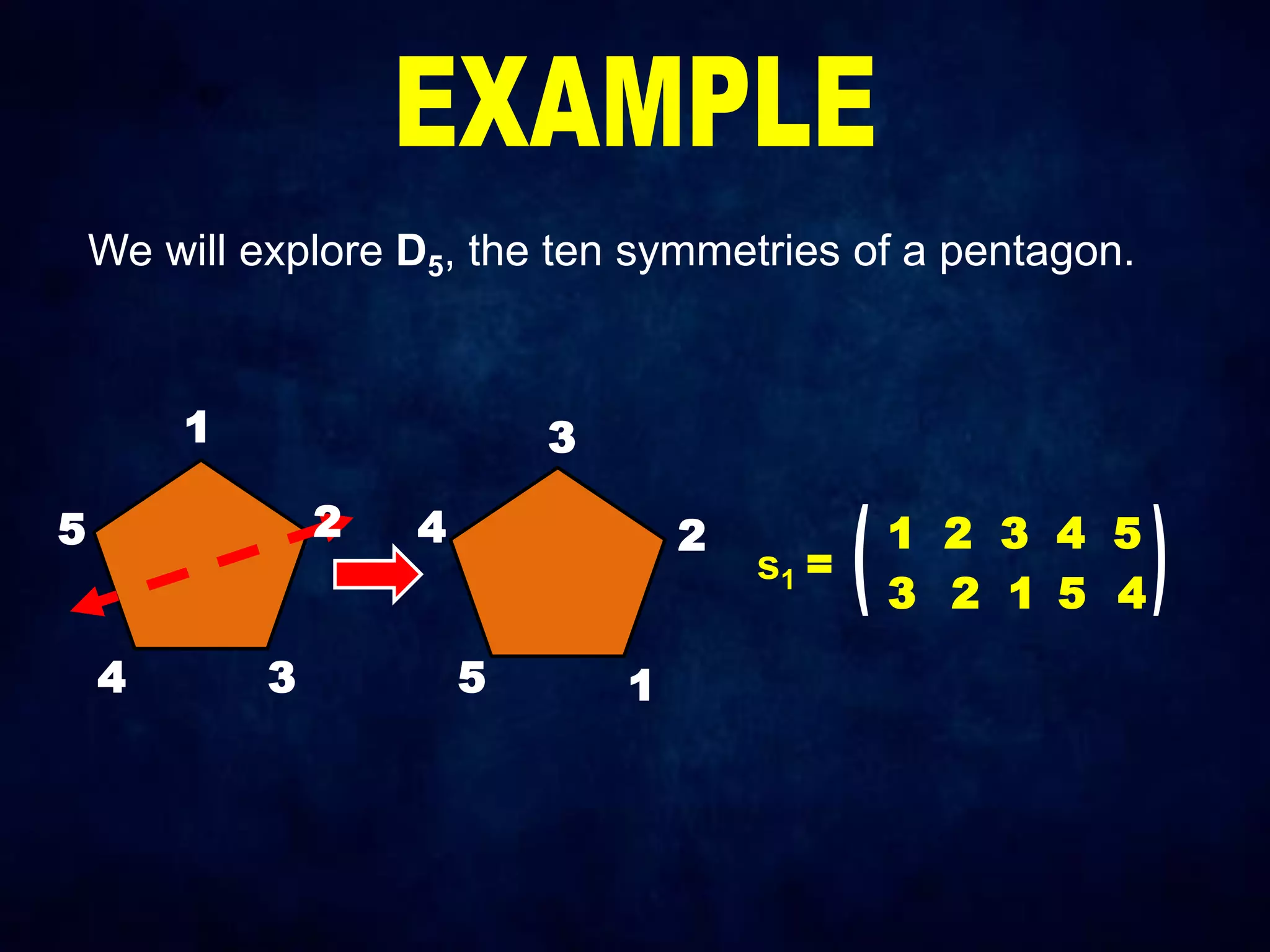
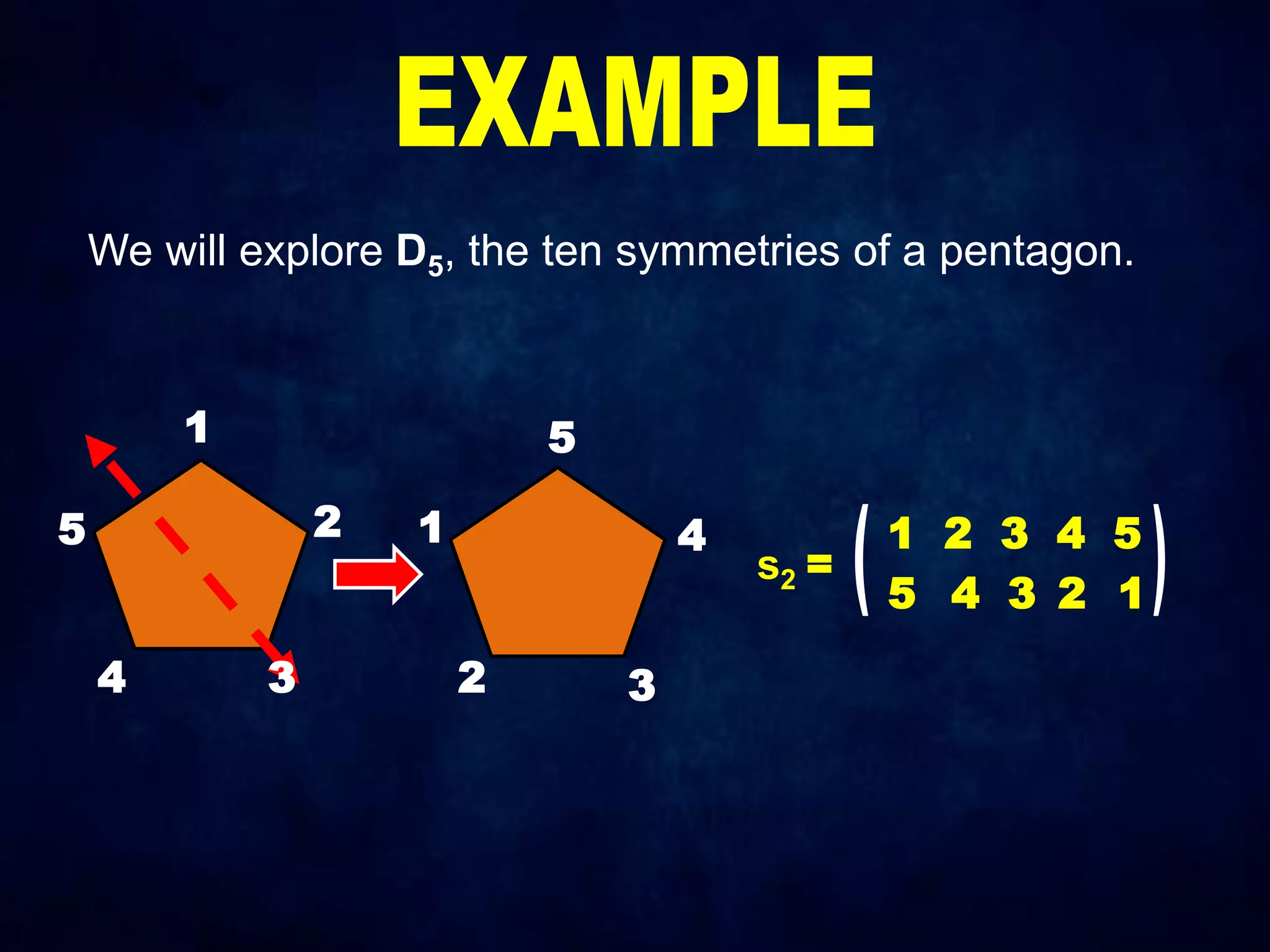
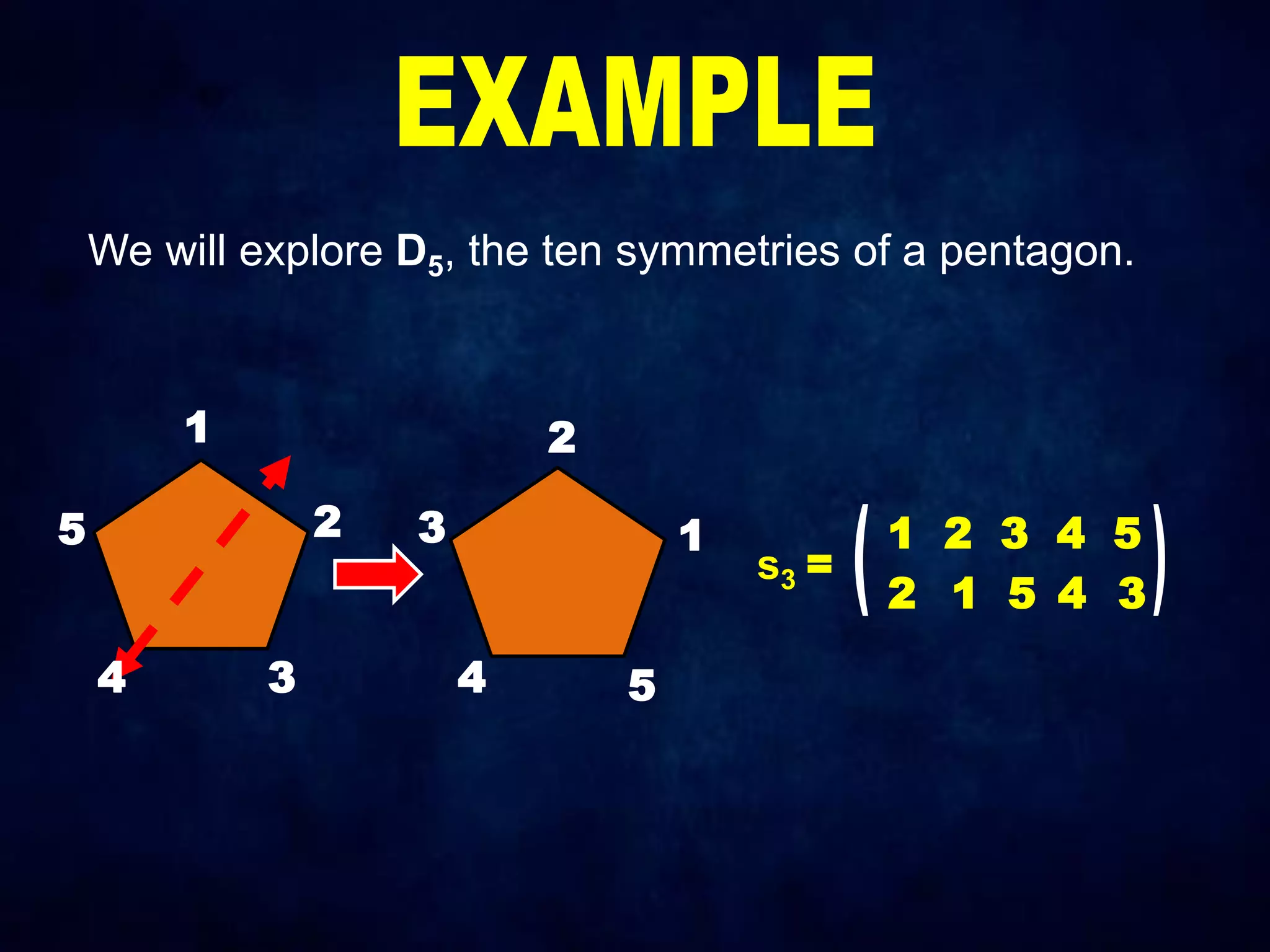
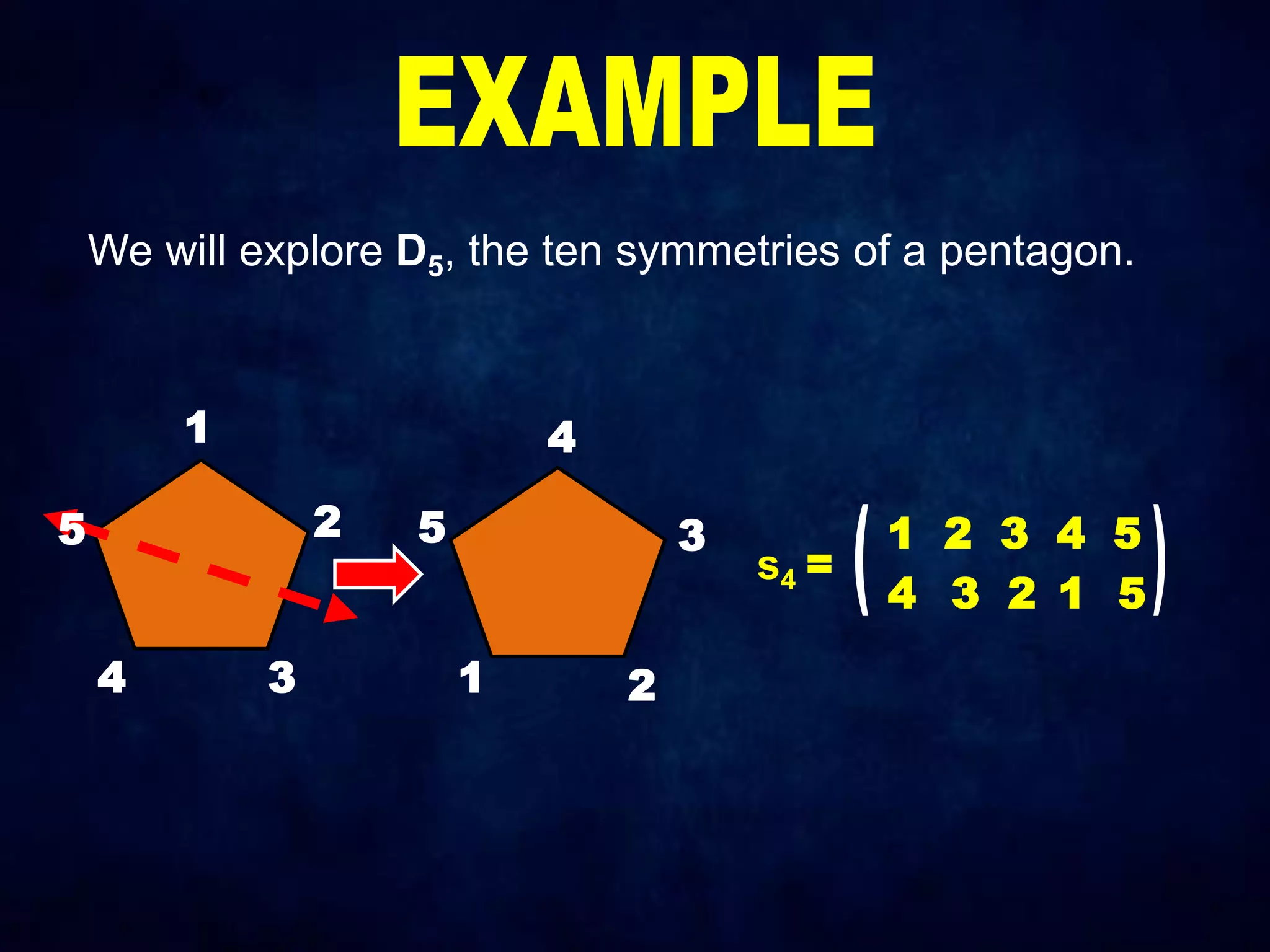
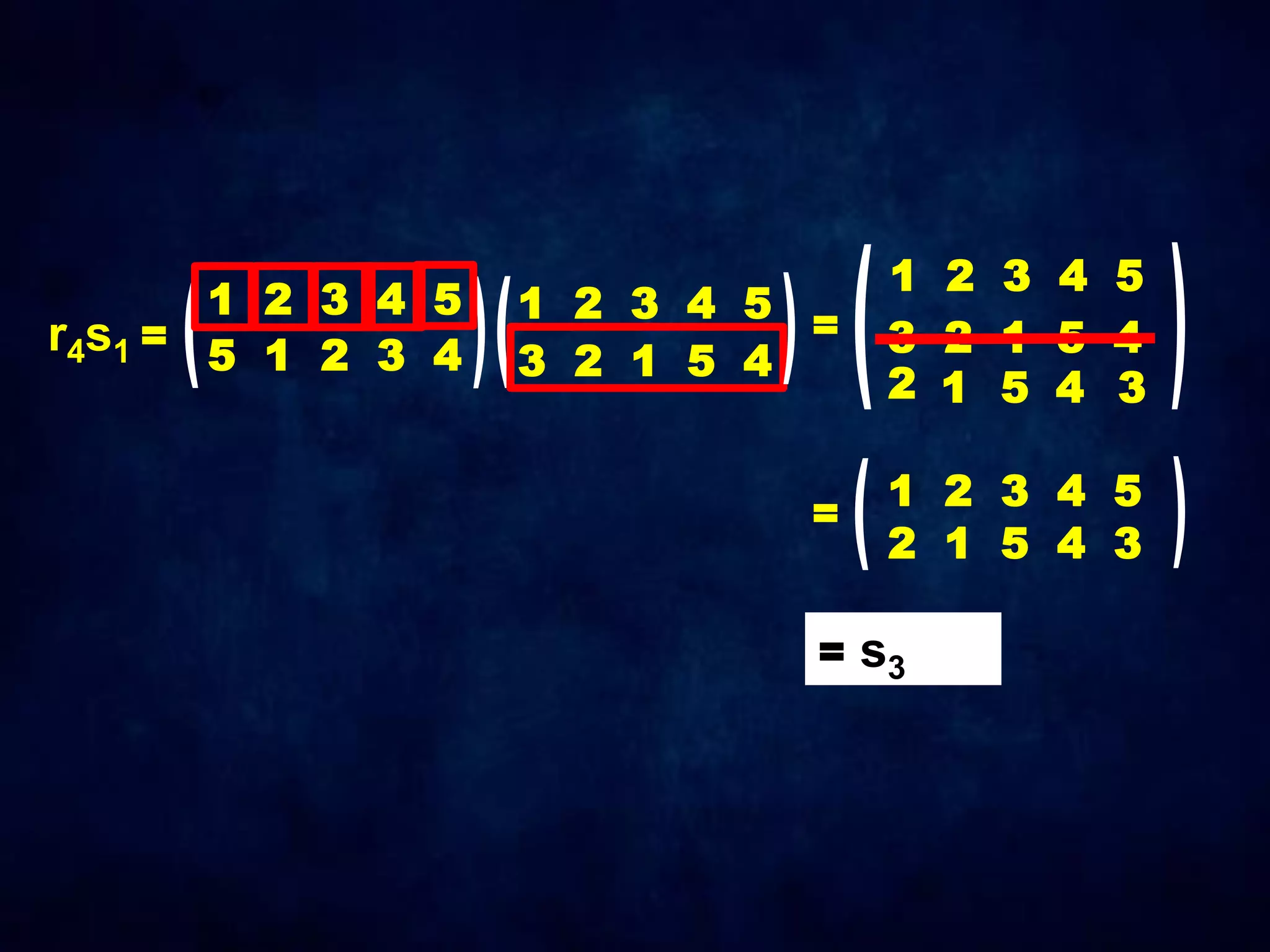
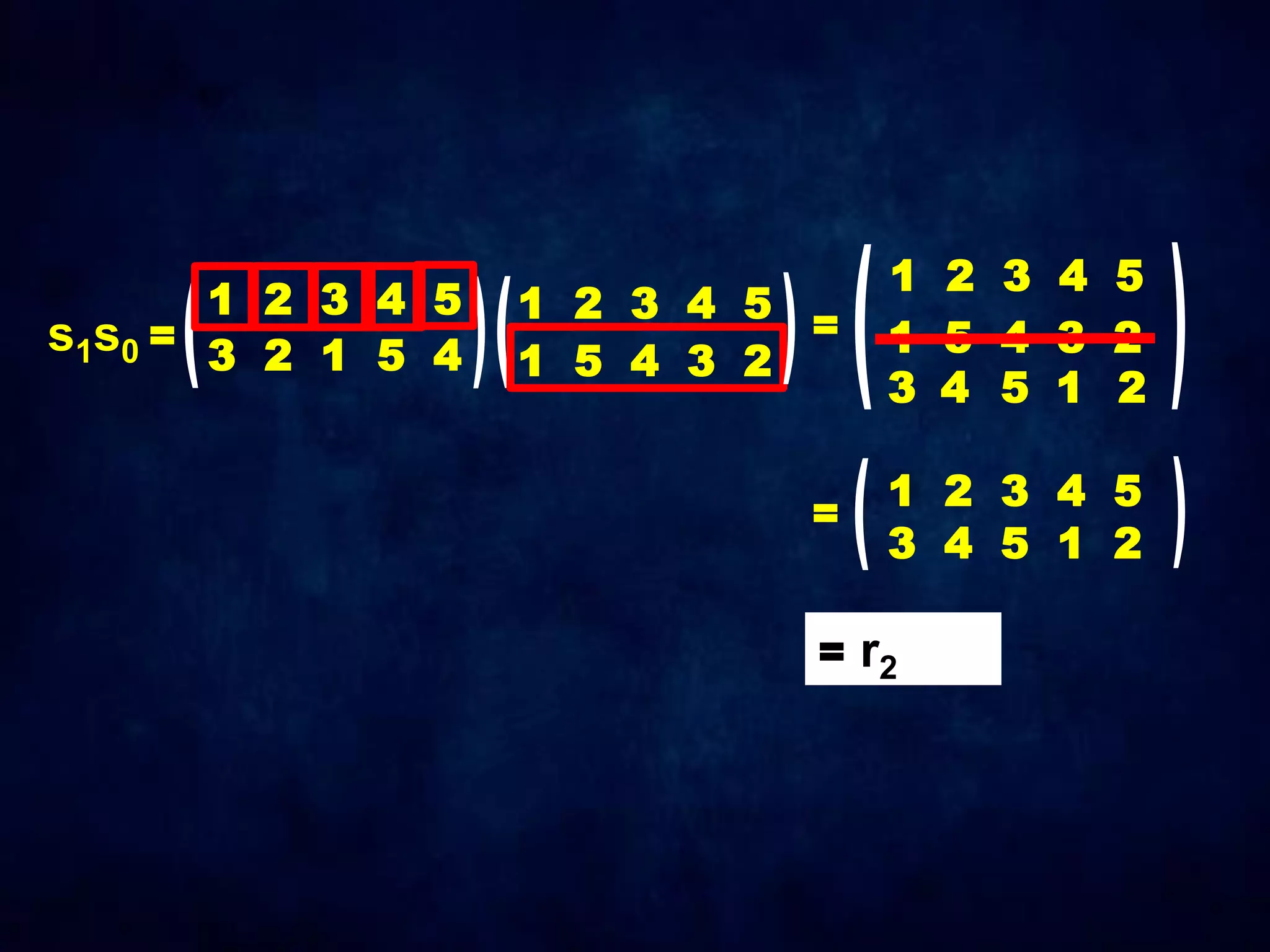
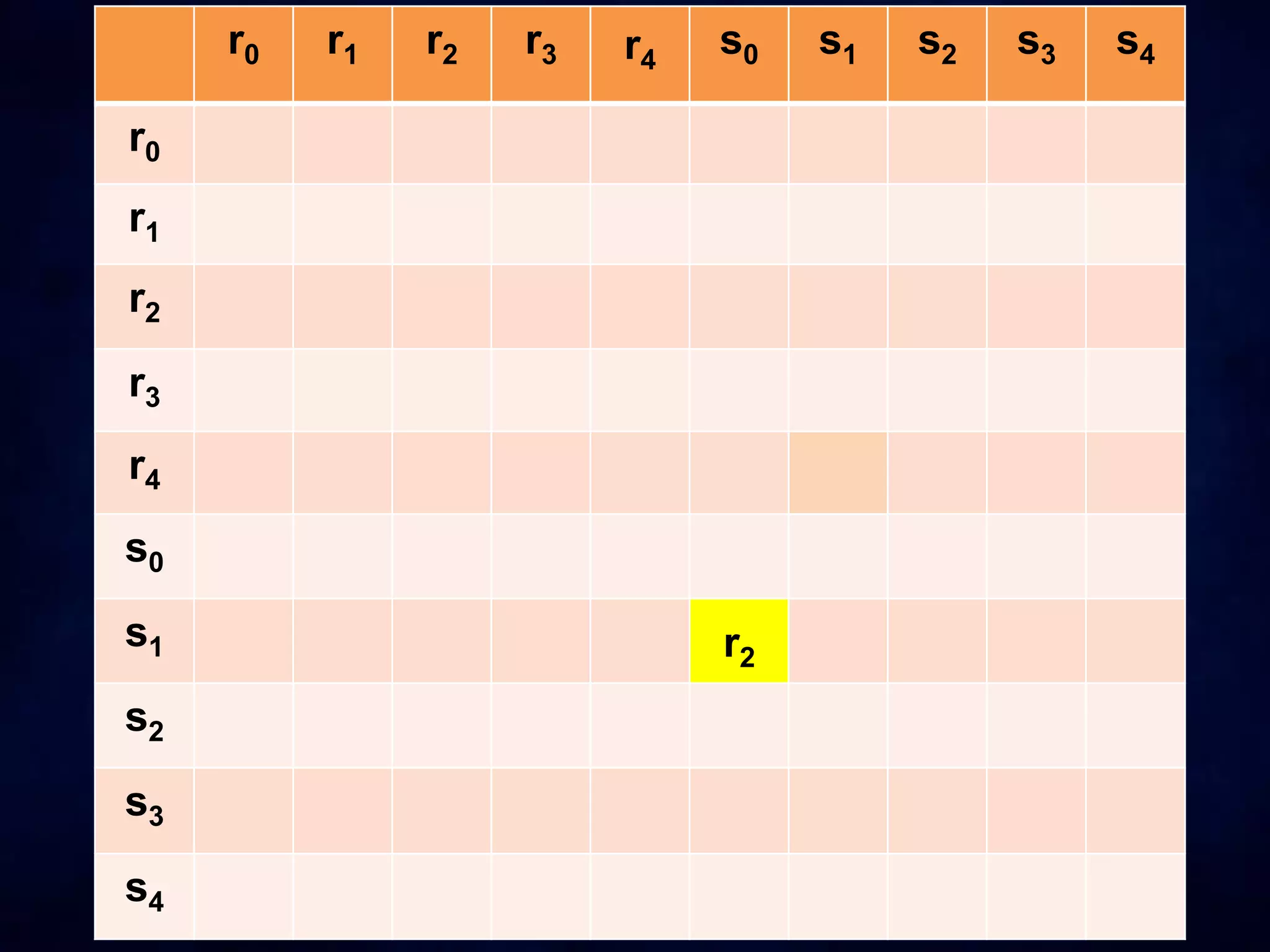
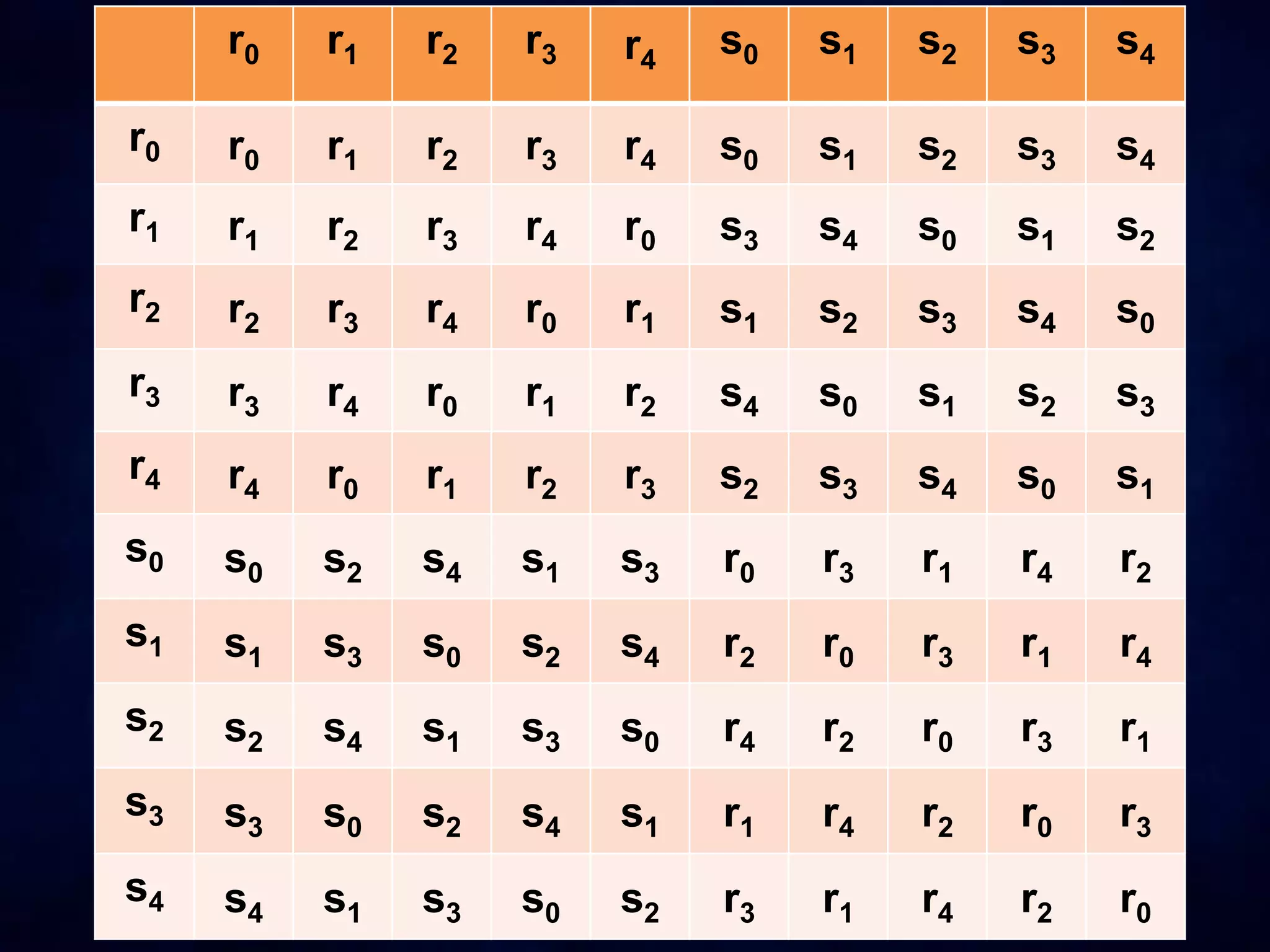
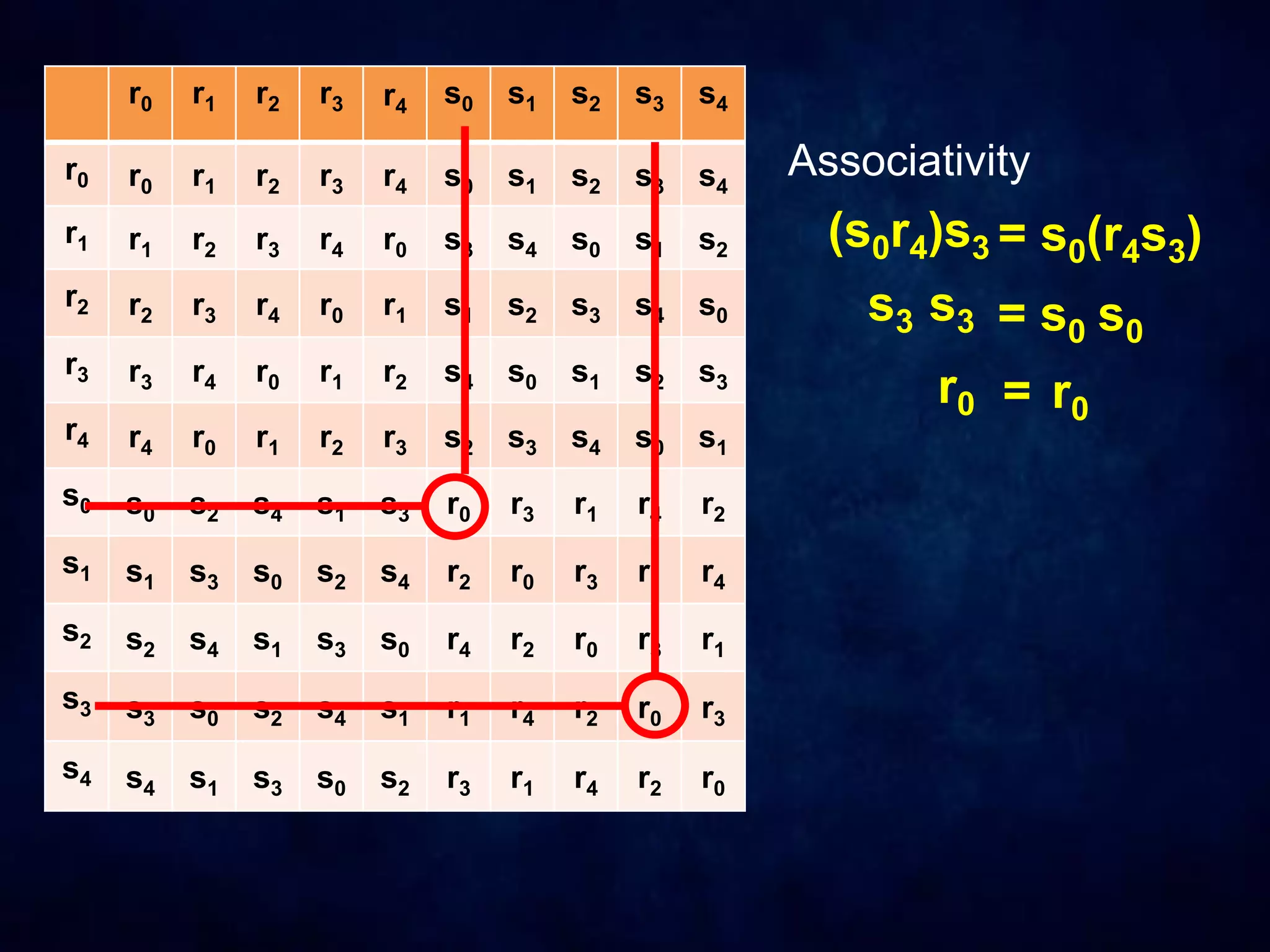
The document discusses dihedral groups Dn, which are the symmetry groups of regular polygons with n sides. It specifically examines D4, the symmetry group of a square with 8 elements - the 4 rotations (r0, r1, r2, r3) and 4 reflections (s0, s1, s2, s3). It then shows that D4 forms a group by verifying the group properties of closure, associativity, identity, and inverse elements. The document will next explore the symmetry group D5 of a pentagon.

Embed presentation

Download to read offline
MTH 601 ABSTRACT ALGEBRA Dihedral Groups and Multiplicative Group Jayson C. Palma (Reporter) PhD Math Student
a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. denoted by Dn
Dn = 2n elements D4 = 2(4) = 8 elements D8 = 2(8) = 16 elements
We will explore D4, the eight symmetries of a square. A B C D A B C D r0 = A B C D A B C D
We will explore D4, the eight symmetries of a square. A B C D D A B C r1 = A B C D B C D A
We will explore D4, the eight symmetries of a square. A B C D C D A B r2 = A B C D C D A B
We will explore D4, the eight symmetries of a square. A B C D B C D A r3 = A B C D D A B C
We will explore D4, the eight symmetries of a square. A B C D D B s0 = A B C D A D C B A C
We will explore D4, the eight symmetries of a square. A C s1 = A B C D C B A D C A D B B D
We will explore D4, the eight symmetries of a square. A B C D C A s2 = A B C D D C B A D B
We will explore D4, the eight symmetries of a square. A B C D A C s3 = A B C D B A D C B D
r0 = A B C D A B C D r1 = A B C D B C D A r2 = A B C D C D A B r3 = A B C D D A B C s0 = A B C D A D C B s1 = A B C D C B A D s2 = A B C D D C B A s3 = A B C D B A D C
r0 r1 r2 r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3
r0r0 = A B C D A B C D A B C D A B C D = A B C D A B C D A B C D A B C D A B C D = = r0
r0 r1 r2 r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r0
r0r1 = A B C D A B C D A B C D B C D A = A B C D B C D A B C D A A B C D B C D A = = r1
r0 r1 r2 r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r1
r0r2 = A B C D A B C D A B C D C D A B = A B C D C D A B C D A B A B C D C D A B = = r2
r0 r1 r2 r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r2
r3s2 = A B C D D A B C A B C D D C B A = A B C D D C B A C B A D A B C D C B A D = = s1
r0 r1 r2 r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 s1
s2s1 = A B C D D C B A A B C D C B A D = A B C D C B A D B C D A A B C D B C D A = = r1
r0 r1 r2 r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r1
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Closure s2s1 = r1 r3s0 = s2
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (r2s1)s3 = r2(s1s3) s0 s3 = r2 r1
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (r2s1)s3 = r2(s1s3) s0 s3 = r2 r1 r3 = r3
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (s0s3)r2 = s0(s3r2) r3 r2 = s0s2
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (s0s3)r2 = s0(s3r2) r3 r2 = s0s2 r1 = r1
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Identity r3e = r3 r3 r0 = r3 e = r0
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Identity s2e = s2 s2 r0 = s2 e = r0
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Inverse s2 a- = e s2 s2= r0
r0 r1 r2 r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Inverse s0 a- = e s0s0 = r0
We will explore D5, the ten symmetries of a pentagon. 1 2 3 4 1 2 3 4 r0 = 1 2 3 4 5 1 2 3 4 5 5 5
We will explore D5, the ten symmetries of a pentagon. 1 2 3 4 5 1 2 3 r1 = 1 2 3 4 5 2 3 4 5 5 4 1
We will explore D5, the ten symmetries of a pentagon. 1 2 3 4 4 5 1 2 r2 = 1 2 3 4 5 3 4 5 1 5 3 2
We will explore D5, the ten symmetries of a pentagon. 1 2 3 4 3 4 5 1 r3 = 1 2 3 4 5 4 5 1 2 5 2 3
We will explore D5, the ten symmetries of a pentagon. 1 2 3 4 2 3 4 5 r4 = 1 2 3 4 5 5 1 2 3 5 1 4
We will explore D5, the ten symmetries of a pentagon. 2 3 4 5 4 3 s0 = 1 2 3 4 5 1 5 4 3 5 2 2 1 1
We will explore D5, the ten symmetries of a pentagon. 1 3 4 1 5 s1 = 1 2 3 4 5 3 2 1 5 5 4 4 3 2 2
We will explore D5, the ten symmetries of a pentagon. 1 2 4 2 s2 = 1 2 3 4 5 5 4 3 2 5 1 1 5 4 3 3
We will explore D5, the ten symmetries of a pentagon. 1 2 3 s3 = 1 2 3 4 5 2 1 5 4 5 3 3 2 1 5 4 4
We will explore D5, the ten symmetries of a pentagon. 1 2 3 4 s4 = 1 2 3 4 5 4 3 2 1 5 4 3 2 1 5 5
r0 = 1 2 3 4 5 1 2 3 4 5 r1 = 1 2 3 4 5 2 3 4 5 1 r2 = 1 2 3 4 5 3 4 5 1 2 r3 = 1 2 3 4 5 4 5 1 2 3 r4 = 1 2 3 4 5 5 1 2 3 4 s0 = 1 2 3 4 5 1 5 4 3 2 s1 = 1 2 3 4 5 3 2 1 5 4 s2 = 1 2 3 4 5 5 4 3 2 1 s3 = 1 2 3 4 5 2 1 5 4 3 s4 = 1 2 3 4 5 4 3 2 1 5
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4
r4s1 = 1 2 3 4 5 5 1 2 3 4 = 2 1 5 4 = = s3 1 2 3 4 5 3 2 1 5 4 1 2 3 4 5 3 2 1 5 4 3 1 2 3 4 5 2 1 5 4 3
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r1 r2 r3 r4 s3 s0 s1 s2 s3 s4
s1s0 = 1 2 3 4 5 3 2 1 5 4 = 3 4 5 1 = = r2 1 2 3 4 5 1 5 4 3 2 1 2 3 4 5 1 5 4 3 2 2 1 2 3 4 5 3 4 5 1 2
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r1 r2 r3 r4 s0 s1 r2 s2 s3 s4
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Closure s3r2 = s2 r4s3 = s0
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Associativity (s0r4)s3 = s0(r4s3) s3 = s0 s3 s0
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Associativity (s0r4)s3 = s0(r4s3) s3 = s0 s3 s0 r0 = r0
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Identity s2 = s2 s2 = s2 r0 e
r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Inverse r4 = e r4 = r0 r1 a-
Dihedral Group Symbol Our Thoughts D1 Shell Petroleum uses the symbol to the left. This shell shape has no rotations (other than the identity) and has only one mirror line (vertical). Therefore, like Mickey Mouse, the figure is said to be bilaterally symmetric and it fits into the category D1. D2 An example of D2 that is easily spotted is the logo for the Columbia Broadcasting System (CBS). The "eye" shape within the circle prevents the figure from being able to rotate by any rotation other than a 1/2 turn. Additionally, the figure has only two ways in which it can be reflected onto itself. D3 The luxury car, Mercedes-Benz, uses a symbol with three rotations and 3 mirror lines. Therefore, the emblem is an example of D3. If we were to convert this figure into a peace sign, however, we would lose 2 of the rotations and two of the reflection lines. This would leave a D1 figure.
D4 The symbol for Purina is a great example of a finite figure of the category D4. It is easy to see that there are four mirror reflections of the figure (one vertical, one horizontal, and two diagonal) as well as four rotations. In other words, rotating the figure four times gives the original figure (the identity). D5 The symbol for Chrysler is a great example of a finite figure of the category D5. In other words, the symbol has five rotations and five axes of reflection. D8 This finite figure is a dihedral group of order 8 due to its eight reflections and eight rotations. The symmetries are created by two squares placed on top of each other and offset by 90 degrees.
In modular arithmetic, the integers coprime (relatively prime) to n from the set {0, 1, …, n-1} of n non-negative integers form a group under multiplication modulo n, called the multiplicative group of integers modulo n. denoted by U(n)
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Closure * 5 * 5 = 1 7 * 3 = 5
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Associativity * (3 * 5) * 1 = 3 * (5 * 1) 7 * 1 = 3 * 5
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Associativity * (3 * 5) * 1 = 3 * (5 * 1) 7 * 1 = 3 * 5 7 = 7
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Identity * 3 * e = 3 3 *1 = 3
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Identity * 7 * e = 7 7 *1 = 7
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Inverse * 7 * a- = e 7 *7 = 1
U(8) = {1, 3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Inverse * 5 * a- = e 5 *5 = 1
Unit II-Lesson 3- Dihedral and Multiplicative Groups (PALMA).pdf

More Related Content

PPT
Resolucion diagrama diagrama Diagramas.ppt
byMartinGonzalez87354
 
PDF
Symbolic Computations in Conformal Geometric Algebra for Three Dimensional O...
byYoshihiro Mizoguchi
 
PDF
Singular value decomposition (SVD)
byLuis Serrano
 
PPTX
Matrix representation of graph
byRounak Biswas
 
PDF
Doc1.doc nobel[1]1
byMark Hilbert
 
PDF
Solucao_Marion_Thornton_Dinamica_Classic (1).pdf
byFranciscoJavierCaedo
 
PDF
Week4
byosamahussien
 
PDF
Mathematics sample assignment
byAll Assignment Experts
 
Resolucion diagrama diagrama Diagramas.ppt
byMartinGonzalez87354
 
Symbolic Computations in Conformal Geometric Algebra for Three Dimensional O...
byYoshihiro Mizoguchi
 
Singular value decomposition (SVD)
byLuis Serrano
 
Matrix representation of graph
byRounak Biswas
 
Doc1.doc nobel[1]1
byMark Hilbert
 
Solucao_Marion_Thornton_Dinamica_Classic (1).pdf
byFranciscoJavierCaedo
 
Week4
byosamahussien
 
Mathematics sample assignment
byAll Assignment Experts
 

Similar to Unit II-Lesson 3- Dihedral and Multiplicative Groups (PALMA).pdf

PDF
Doc1.doc nobel[1]2
byMark Hilbert
 
PDF
Doc1.doc nobel[1]1[1]
byMark Hilbert
 
PDF
Doc1.doc nobel[1]3
byMark Hilbert
 
PPTX
graph theory
byShashank Singh
 
PPTX
Tutorial 0 mth 3201
byDrradz Maths
 
PPT
Alignment scoring functions
byavrilcoghlan
 
PPTX
Relations
byAkkradet Keawyoo
 
PDF
The shortest distance between skew lines
byTarun Gehlot
 
PPTX
NDA-Mathematics.pptx djfjsdjfbdjbfjdbjfbjd
byramkiran1907
 
PPT
The fourier series signals and systems by R ismail
byRumaisa35
 
PDF
Latex Symbols.pdf
byKomal526846
 
PDF
Brian Covello: Research in Mathematical Group Representation Theory and Symmetry
byBrian Covello
 
PDF
Serpent sboxes
byAbrar Ahmad
 
PPTX
Square Peg Problem Test Function
bySing Kuang Tan
 
PDF
Permutations 2020
byRobert Geofroy
 
PDF
Tot d sokal
byΣωκράτης Ρωμανίδης
 
PPT
Operational research
byAlbi Thomas
 
PDF
AlgoPerm2012 - 03 Olivier Hudry
byAlgoPerm 2012
 
PDF
Tutorial 6 mth 3201
byDrradz Maths
 
PDF
Suborbits and suborbital graphs of the symmetric group acting on ordered r ...
byAlexander Decker
 
Doc1.doc nobel[1]2
byMark Hilbert
 
Doc1.doc nobel[1]1[1]
byMark Hilbert
 
Doc1.doc nobel[1]3
byMark Hilbert
 
graph theory
byShashank Singh
 
Tutorial 0 mth 3201
byDrradz Maths
 
Alignment scoring functions
byavrilcoghlan
 
Relations
byAkkradet Keawyoo
 
The shortest distance between skew lines
byTarun Gehlot
 
NDA-Mathematics.pptx djfjsdjfbdjbfjdbjfbjd
byramkiran1907
 
The fourier series signals and systems by R ismail
byRumaisa35
 
Latex Symbols.pdf
byKomal526846
 
Brian Covello: Research in Mathematical Group Representation Theory and Symmetry
byBrian Covello
 
Serpent sboxes
byAbrar Ahmad
 
Square Peg Problem Test Function
bySing Kuang Tan
 
Permutations 2020
byRobert Geofroy
 
Tot d sokal
byΣωκράτης Ρωμανίδης
 
Operational research
byAlbi Thomas
 
AlgoPerm2012 - 03 Olivier Hudry
byAlgoPerm 2012
 
Tutorial 6 mth 3201
byDrradz Maths
 
Suborbits and suborbital graphs of the symmetric group acting on ordered r ...
byAlexander Decker
 

Recently uploaded

PPTX
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PPTX
PARENTAL ROUTES OF DRUGS ADMINISTRATION .pptx
byAneetaSharma15
 
PDF
The voice of the rain poem class 11th.pdf
byReeta Baral
 
PPTX
Repeat Orders_ Use Odoo Blanket Agreement
byCeline George
 
PDF
Most Imp Chapters & Weightage for Boards 2025.pdf
byTamannaSagar
 
PPTX
Steve Hale - Developing Elite Young Goalkeepers 2024.pptx
bypjmfd
 
PDF
IMANI Africa files RTI request seeking full disclosure on 2026 SIM registrati...
bynservice241
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PPTX
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
PPTX
UNIT 1: COMMUNICATION SKILLS, BARRIERS TO COMMUNICATION, PERSPECTIVES IN COMM...
byPOOJA KARVANDE
 
PDF
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
PDF
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
PPTX
Nursing Unit Management, patient care unit, physical layout of nursing unit,t...
byyellow4878
 
PPTX
Partial Correlation of Coefficient - Values of r₁₂.₃, r₂₃.₁ & r₁₃.₂
bySundar B N
 
PPTX
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
PDF
Micro Economics for class 12 and class 11
bysurajbajaj4116
 
PPTX
Introduction-to-Anatomy-and-Physiology.pptx
byAshish Umale
 
PPTX
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
PPTX
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PARENTAL ROUTES OF DRUGS ADMINISTRATION .pptx
byAneetaSharma15
 
The voice of the rain poem class 11th.pdf
byReeta Baral
 
Repeat Orders_ Use Odoo Blanket Agreement
byCeline George
 
Most Imp Chapters & Weightage for Boards 2025.pdf
byTamannaSagar
 
Steve Hale - Developing Elite Young Goalkeepers 2024.pptx
bypjmfd
 
IMANI Africa files RTI request seeking full disclosure on 2026 SIM registrati...
bynservice241
 
Analyzing the data of your initial survey
byThelma Villaflores
 
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
UNIT 1: COMMUNICATION SKILLS, BARRIERS TO COMMUNICATION, PERSPECTIVES IN COMM...
byPOOJA KARVANDE
 
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
Nursing Unit Management, patient care unit, physical layout of nursing unit,t...
byyellow4878
 
Partial Correlation of Coefficient - Values of r₁₂.₃, r₂₃.₁ & r₁₃.₂
bySundar B N
 
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
Micro Economics for class 12 and class 11
bysurajbajaj4116
 
Introduction-to-Anatomy-and-Physiology.pptx
byAshish Umale
 
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 

Unit II-Lesson 3- Dihedral and Multiplicative Groups (PALMA).pdf

  • 1.
    MTH 601 ABSTRACTALGEBRA Dihedral Groups and Multiplicative Group Jayson C. Palma (Reporter) PhD Math Student
  • 2.
    a dihedral groupis the group of symmetries of a regular polygon, which includes rotations and reflections. denoted by Dn
  • 3.
    Dn = 2nelements D4 = 2(4) = 8 elements D8 = 2(8) = 16 elements
  • 4.
    We will exploreD4, the eight symmetries of a square. A B C D A B C D r0 = A B C D A B C D
  • 5.
    We will exploreD4, the eight symmetries of a square. A B C D D A B C r1 = A B C D B C D A
  • 6.
    We will exploreD4, the eight symmetries of a square. A B C D C D A B r2 = A B C D C D A B
  • 7.
    We will exploreD4, the eight symmetries of a square. A B C D B C D A r3 = A B C D D A B C
  • 8.
    We will exploreD4, the eight symmetries of a square. A B C D D B s0 = A B C D A D C B A C
  • 9.
    We will exploreD4, the eight symmetries of a square. A C s1 = A B C D C B A D C A D B B D
  • 10.
    We will exploreD4, the eight symmetries of a square. A B C D C A s2 = A B C D D C B A D B
  • 11.
    We will exploreD4, the eight symmetries of a square. A B C D A C s3 = A B C D B A D C B D
  • 12.
    r0 = A BC D A B C D r1 = A B C D B C D A r2 = A B C D C D A B r3 = A B C D D A B C s0 = A B C D A D C B s1 = A B C D C B A D s2 = A B C D D C B A s3 = A B C D B A D C
  • 13.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3
  • 14.
    r0r0 = A BC D A B C D A B C D A B C D = A B C D A B C D A B C D A B C D A B C D = = r0
  • 15.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r0
  • 16.
    r0r1 = A BC D A B C D A B C D B C D A = A B C D B C D A B C D A A B C D B C D A = = r1
  • 17.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r1
  • 18.
    r0r2 = A BC D A B C D A B C D C D A B = A B C D C D A B C D A B A B C D C D A B = = r2
  • 19.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r2
  • 20.
    r3s2 = A BC D D A B C A B C D D C B A = A B C D D C B A C B A D A B C D C B A D = = s1
  • 21.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 s1
  • 22.
    s2s1 = A BC D D C B A A B C D C B A D = A B C D C B A D B C D A A B C D B C D A = = r1
  • 23.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r1 r2 r3 s0 s1 s2 s3 r1
  • 24.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0
  • 25.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Closure s2s1 = r1 r3s0 = s2
  • 26.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (r2s1)s3 = r2(s1s3) s0 s3 = r2 r1
  • 27.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (r2s1)s3 = r2(s1s3) s0 s3 = r2 r1 r3 = r3
  • 28.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (s0s3)r2 = s0(s3r2) r3 r2 = s0s2
  • 29.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Associativity (s0s3)r2 = s0(s3r2) r3 r2 = s0s2 r1 = r1
  • 30.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Identity r3e = r3 r3 r0 = r3 e = r0
  • 31.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Identity s2e = s2 s2 r0 = s2 e = r0
  • 32.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Inverse s2 a- = e s2 s2= r0
  • 33.
    r0 r1 r2r3 s0 s1 s2 s3 r0 r0 r1 r2 r3 s0 s1 s2 s3 r1 r1 r2 r3 r0 s3 s2 s0 s1 r2 r2 r3 r0 r1 s1 s0 s3 s2 r3 r3 r0 r1 r2 s2 s3 s1 s0 s0 s0 s2 s1 s3 r0 r2 r1 r3 s1 s1 s3 s0 s2 r2 r0 r3 r1 s2 s2 s1 s3 s0 r3 r1 r0 r2 s3 s3 s0 s2 s1 r1 r3 r2 r0 Inverse s0 a- = e s0s0 = r0
  • 34.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 4 1 2 3 4 r0 = 1 2 3 4 5 1 2 3 4 5 5 5
  • 35.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 4 5 1 2 3 r1 = 1 2 3 4 5 2 3 4 5 5 4 1
  • 36.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 4 4 5 1 2 r2 = 1 2 3 4 5 3 4 5 1 5 3 2
  • 37.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 4 3 4 5 1 r3 = 1 2 3 4 5 4 5 1 2 5 2 3
  • 38.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 4 2 3 4 5 r4 = 1 2 3 4 5 5 1 2 3 5 1 4
  • 39.
    We will exploreD5, the ten symmetries of a pentagon. 2 3 4 5 4 3 s0 = 1 2 3 4 5 1 5 4 3 5 2 2 1 1
  • 40.
    We will exploreD5, the ten symmetries of a pentagon. 1 3 4 1 5 s1 = 1 2 3 4 5 3 2 1 5 5 4 4 3 2 2
  • 41.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 4 2 s2 = 1 2 3 4 5 5 4 3 2 5 1 1 5 4 3 3
  • 42.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 s3 = 1 2 3 4 5 2 1 5 4 5 3 3 2 1 5 4 4
  • 43.
    We will exploreD5, the ten symmetries of a pentagon. 1 2 3 4 s4 = 1 2 3 4 5 4 3 2 1 5 4 3 2 1 5 5
  • 44.
    r0 = 1 23 4 5 1 2 3 4 5 r1 = 1 2 3 4 5 2 3 4 5 1 r2 = 1 2 3 4 5 3 4 5 1 2 r3 = 1 2 3 4 5 4 5 1 2 3 r4 = 1 2 3 4 5 5 1 2 3 4 s0 = 1 2 3 4 5 1 5 4 3 2 s1 = 1 2 3 4 5 3 2 1 5 4 s2 = 1 2 3 4 5 5 4 3 2 1 s3 = 1 2 3 4 5 2 1 5 4 3 s4 = 1 2 3 4 5 4 3 2 1 5
  • 45.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4
  • 46.
    r4s1 = 1 23 4 5 5 1 2 3 4 = 2 1 5 4 = = s3 1 2 3 4 5 3 2 1 5 4 1 2 3 4 5 3 2 1 5 4 3 1 2 3 4 5 2 1 5 4 3
  • 47.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r1 r2 r3 r4 s3 s0 s1 s2 s3 s4
  • 48.
    s1s0 = 1 23 4 5 3 2 1 5 4 = 3 4 5 1 = = r2 1 2 3 4 5 1 5 4 3 2 1 2 3 4 5 1 5 4 3 2 2 1 2 3 4 5 3 4 5 1 2
  • 49.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r1 r2 r3 r4 s0 s1 r2 s2 s3 s4
  • 50.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0
  • 51.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Closure s3r2 = s2 r4s3 = s0
  • 52.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Associativity (s0r4)s3 = s0(r4s3) s3 = s0 s3 s0
  • 53.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Associativity (s0r4)s3 = s0(r4s3) s3 = s0 s3 s0 r0 = r0
  • 54.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Identity s2 = s2 s2 = s2 r0 e
  • 55.
    r0 r1 r2r3 r4 s0 s1 s2 s3 s4 r0 r0 r1 r2 r3 r4 s0 s1 s2 s3 s4 r1 r1 r2 r3 r4 r0 s3 s4 s0 s1 s2 r2 r2 r3 r4 r0 r1 s1 s2 s3 s4 s0 r3 r3 r4 r0 r1 r2 s4 s0 s1 s2 s3 r4 r4 r0 r1 r2 r3 s2 s3 s4 s0 s1 s0 s0 s2 s4 s1 s3 r0 r3 r1 r4 r2 s1 s1 s3 s0 s2 s4 r2 r0 r3 r1 r4 s2 s2 s4 s1 s3 s0 r4 r2 r0 r3 r1 s3 s3 s0 s2 s4 s1 r1 r4 r2 r0 r3 s4 s4 s1 s3 s0 s2 r3 r1 r4 r2 r0 Inverse r4 = e r4 = r0 r1 a-
  • 56.
    Dihedral Group Symbol Our Thoughts D1 ShellPetroleum uses the symbol to the left. This shell shape has no rotations (other than the identity) and has only one mirror line (vertical). Therefore, like Mickey Mouse, the figure is said to be bilaterally symmetric and it fits into the category D1. D2 An example of D2 that is easily spotted is the logo for the Columbia Broadcasting System (CBS). The "eye" shape within the circle prevents the figure from being able to rotate by any rotation other than a 1/2 turn. Additionally, the figure has only two ways in which it can be reflected onto itself. D3 The luxury car, Mercedes-Benz, uses a symbol with three rotations and 3 mirror lines. Therefore, the emblem is an example of D3. If we were to convert this figure into a peace sign, however, we would lose 2 of the rotations and two of the reflection lines. This would leave a D1 figure.
  • 57.
    D4 The symbol forPurina is a great example of a finite figure of the category D4. It is easy to see that there are four mirror reflections of the figure (one vertical, one horizontal, and two diagonal) as well as four rotations. In other words, rotating the figure four times gives the original figure (the identity). D5 The symbol for Chrysler is a great example of a finite figure of the category D5. In other words, the symbol has five rotations and five axes of reflection. D8 This finite figure is a dihedral group of order 8 due to its eight reflections and eight rotations. The symmetries are created by two squares placed on top of each other and offset by 90 degrees.
  • 58.
    In modular arithmetic,the integers coprime (relatively prime) to n from the set {0, 1, …, n-1} of n non-negative integers form a group under multiplication modulo n, called the multiplicative group of integers modulo n. denoted by U(n)
  • 59.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Closure * 5 * 5 = 1 7 * 3 = 5
  • 60.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Associativity * (3 * 5) * 1 = 3 * (5 * 1) 7 * 1 = 3 * 5
  • 61.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Associativity * (3 * 5) * 1 = 3 * (5 * 1) 7 * 1 = 3 * 5 7 = 7
  • 62.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Identity * 3 * e = 3 3 *1 = 3
  • 63.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Identity * 7 * e = 7 7 *1 = 7
  • 64.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Inverse * 7 * a- = e 7 *7 = 1
  • 65.
    U(8) = {1,3, 5, 7} Binary operation: Multiplication modulo 8 Lets construct the group table for U(8) 1 3 5 7 1 3 5 7 1 3 5 7 3 1 7 5 5 7 1 3 7 5 3 1 Group Properties Inverse * 5 * a- = e 5 *5 = 1