The document describes applying the Mason's rule method to calculate the transfer function Tt of a network with multiple loops. It identifies 6 loops (L1-L6) in the network and calculates the terms needed for the Tt formula, including the individual path functions (T1-T4), the Δi values, and the ΔT denominator term. It then applies the Tt formula to calculate the overall transfer function of the network.

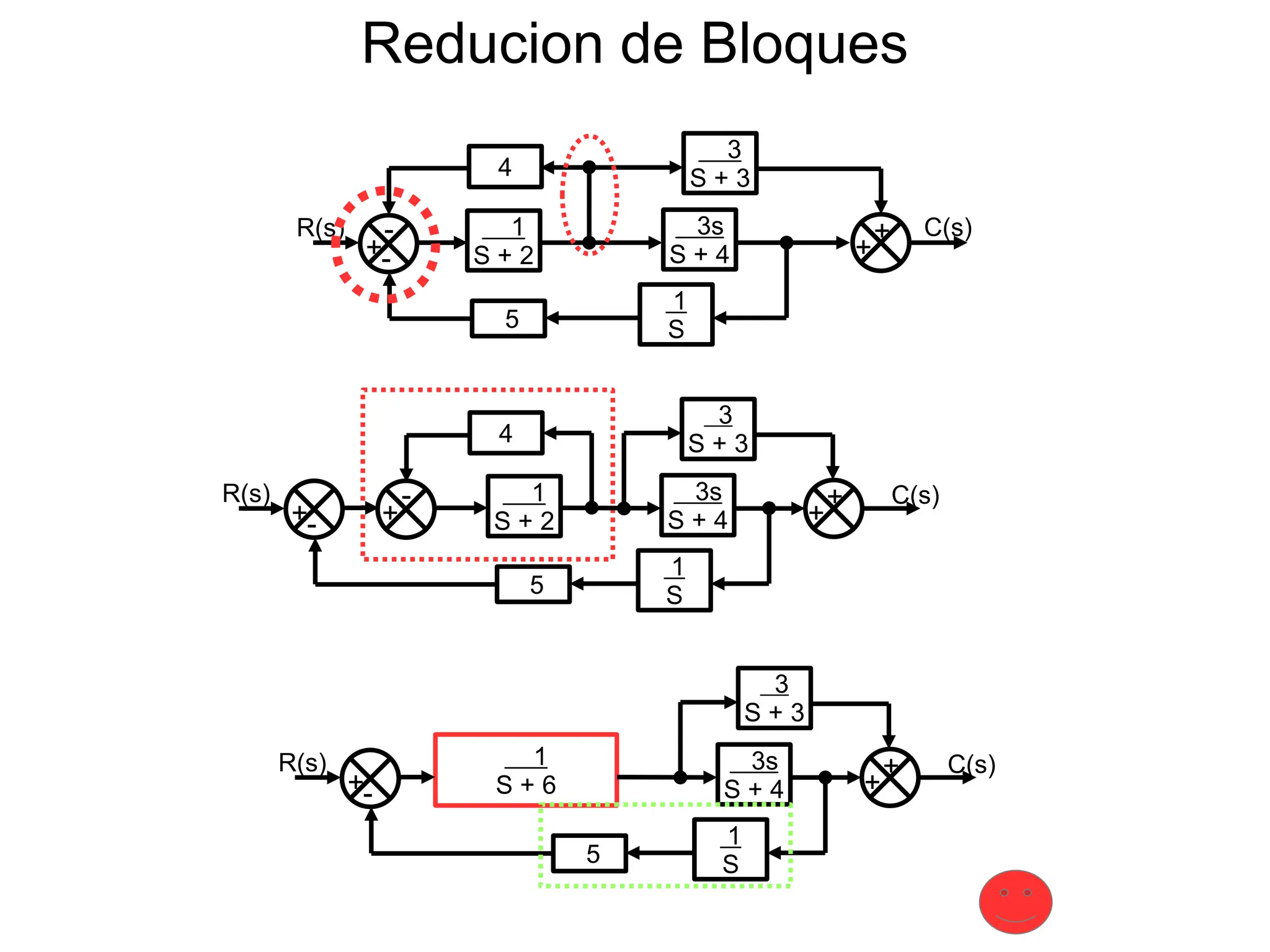
1. Reducion de Bloques
1
S + 2
4
3s
S + 4
3
S + 3
5
1
S
+
+
-
+
-
R(s) C(s)
1
S + 2
4
3s
S + 4
3
S + 3
5
1
S
+
+
-
+
R(s) C(s)
+
-
1
S + 6
3s
S + 4
3
S + 3
5
1
S
+
+
-
+
R(s) C(s)

2. 1
S + 6
3s
S + 4
3
S + 3
5
S
+
+
-
+
R(s) C(s)
1
S + 6
3s
S + 4
3
S + 3
5
S
+
+
-
+
R(s) C(s)
s+4
3s
1
S + 6
3s
S + 4
3
S + 3
5
S
+
+
-
+
R(s) C(s)
s+4
3s
1
(s+6)(s+4)
5
S
+
+
-
+
R(s) C(s)
(s+4)
s(s+3)
3s
(s+6)(s+4) + 15
s(s+3)+ (s+4)
[s(s+3)]
R(s) C(s)
3s (s+3) +3 (s+4)
[(s+6)(s+4) +15](s+3)
R(s) C(s)

3. Reducion de Señales
1/S 1/S
1 b2
-a1
-a2
R(s) C(s)
b1
1/S 1/S
1 b2
-a1
-a2
R(s) C(s)
b1
1 1
1/(s+a1) 1/S
1 b2
-a2
R(s)
C(s)
b1
1 1
1/(s+a1) 1/S
1 b2
-a2
R(s)
C(s)
b1
1
1/(s+a1)
1/(s+a1) 1/S
1 b2
-a2
R(s)
C(s)
b1
1
1/(s+a1)
1/b2

4. Reducion de Señales
1/S 1/S
1 b2
-a1
-a2
R(s) C(s)
b1
1/S 1/S
1 b2
-a1
-a2
R(s) C(s)
b1
1 1
1/(s+a1) 1/S
1 b2
-a2
R(s)
C(s)
b1
1 1
1/(s+a1) 1/S
1 b2
-a2
R(s)
C(s)
b1
1
1/(s+a1)
1/(s+a1) 1/S
1 b2
-a2
R(s)
C(s)
b1
1
1/(s+a1)
1/b2

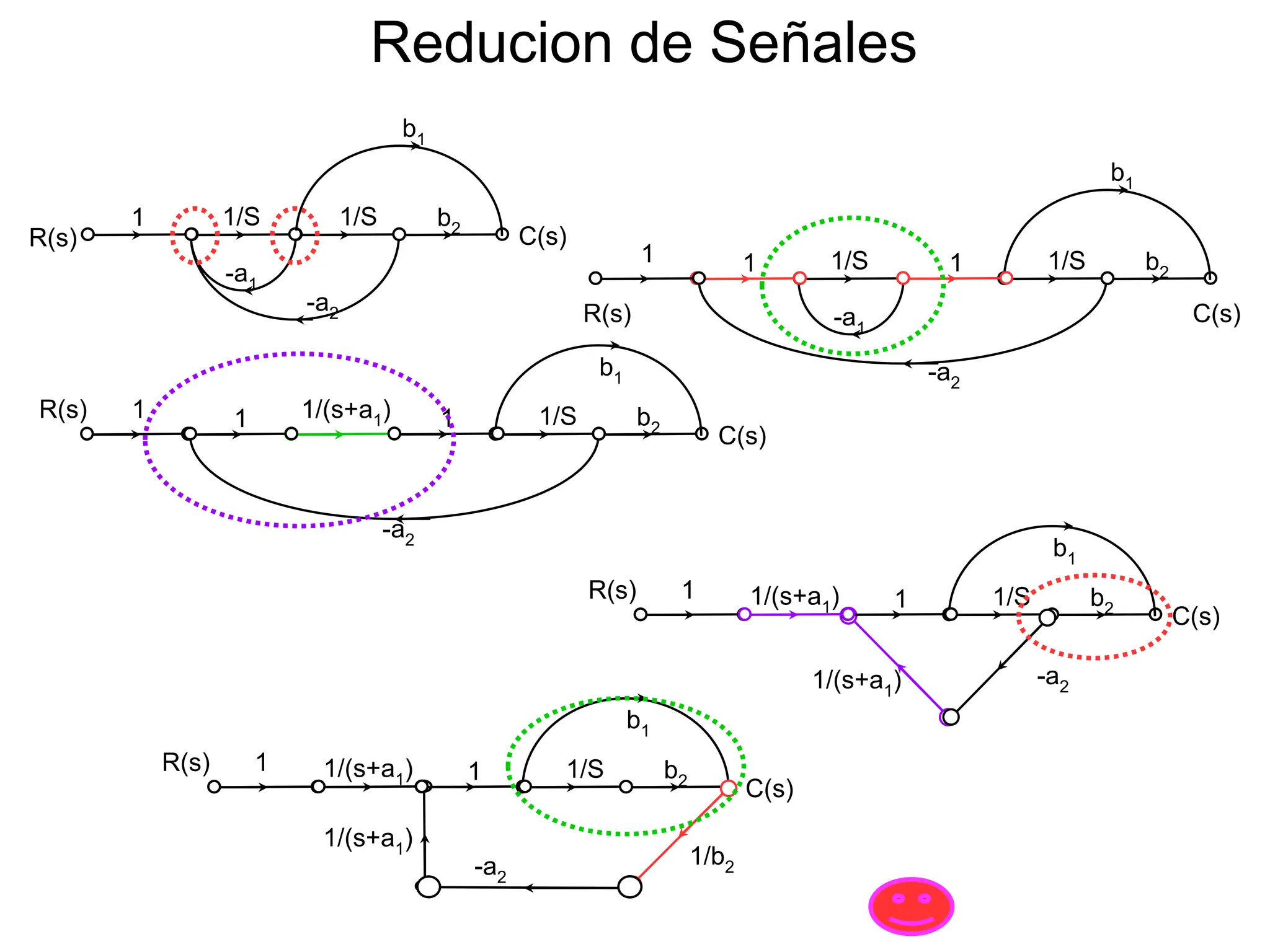
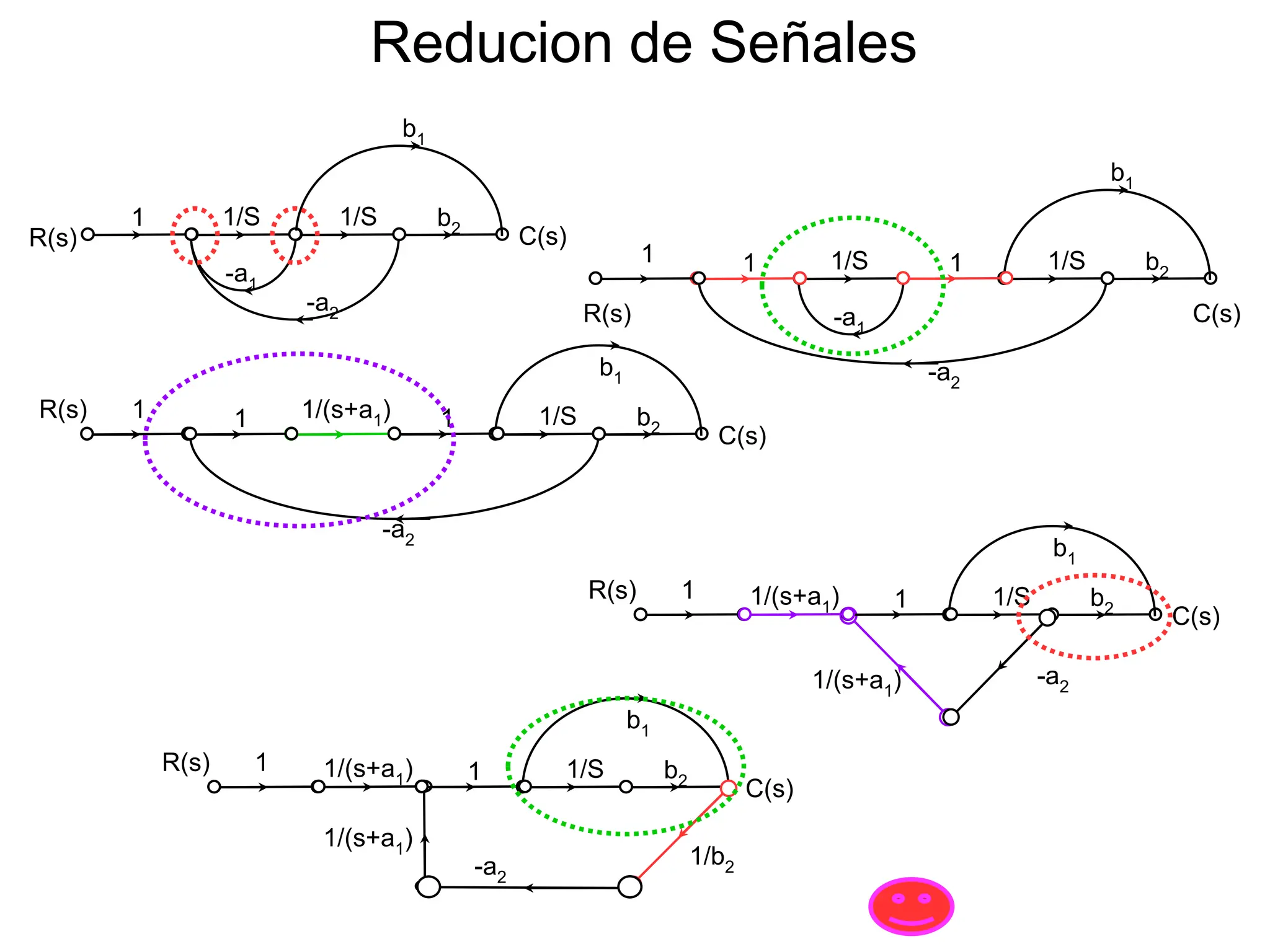
5. 1/(s+a1) b1+1/(sb2 )
1
-a2
R(s)
C(s)
1
1/(s+a1)
1/b2
1/(s+a1)
R(s)
1 G1 1
C(s
)
1/(s+a1)
R(s) C(s)
1 b1+1/(sb2 )
1
-a2(1/b2)[1/(s+a)]
G1=
b1+
1
sb2
1+ [b1 +
1
sb2
][
a2
b2 (s+ a1)
]
Gs
R(s)
1 1
C(s
)
Gs=
1
(s+ a1)
b1+
1
sb2
1+ [b1 +
1
sb2
][
a2
b2 (s+ a1)
]
Gs=
1
(s+ a1)
[(b1 sb2)+ 1]/sb2
1+ [
(b1 sb2)+ 1
sb2
][
a2
b2 (s+ a1)
]
Gs=
(b1 sb2)+ 1
(sb2)(s+ a1)+ [(b1 sb2)+ 1][
a2
b2
]

6. Método de Mason
R(S)
C(s)
1
1
x4
x2 x3 x5
x8
x7 x6
x9
xA
x1 b c d
i h g f e
j
k
m
p
a
o

7. Las trayectorias
directas son los
caminos desde
una entrada
hasta una salida
sin repetir nodo.
T1(x18A) = i . k
T2(x1234567A) = a.b.c.d.e.o.m
T3(x123457A) = a.b.c.d.f.m
T4(x1238A) = a.b.h.k

8. IDENTIFICAR TODOS LOS LAZOS
L1 = x18A9 = ikpj
L2 = x3457 = cdfg
L3 = x34567 = cdeog
L4 = x1238A9 = abhkpj
L5 = x123457A9 = abcdfmpj
L6 = x1234567A9 = abcdeompj

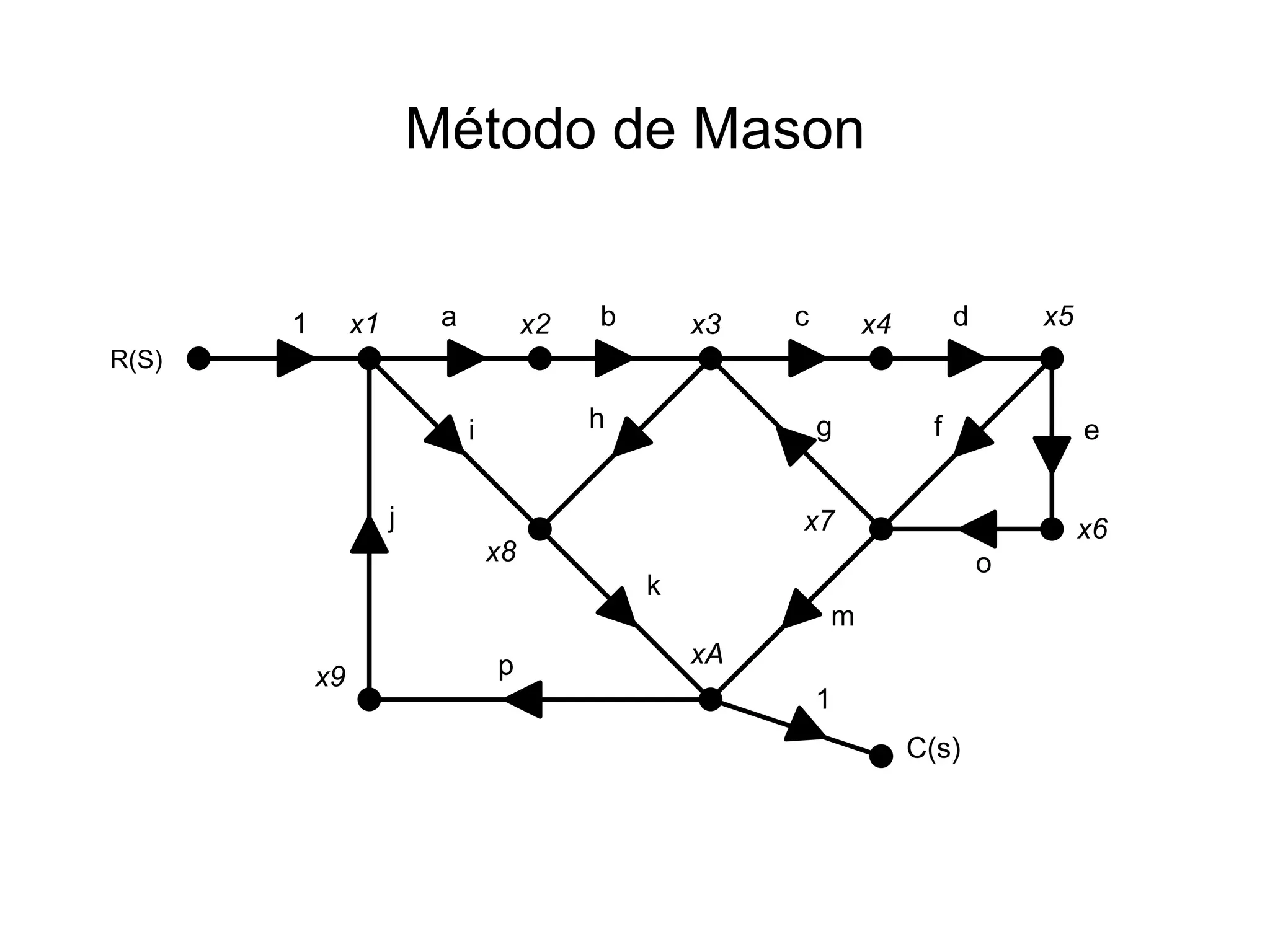
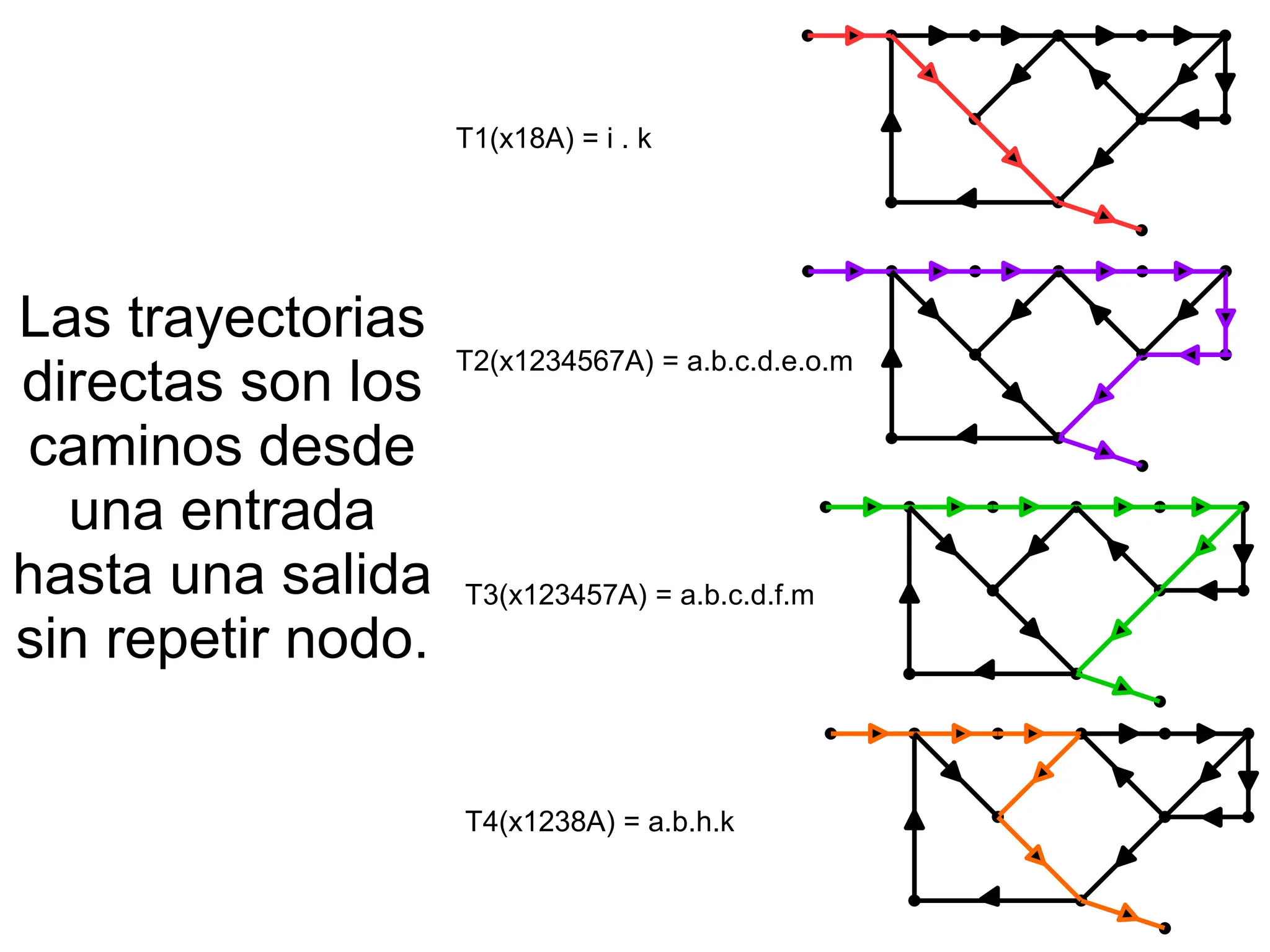
9. Con esos datos la formula es:
Tt=
∑
i
Ti .△i
△T
△T= 1− ∑
a
La+ ∑
a,b
La .Lb− ∑
a,b,c
La .Lb .Lc+ ....
∑
a
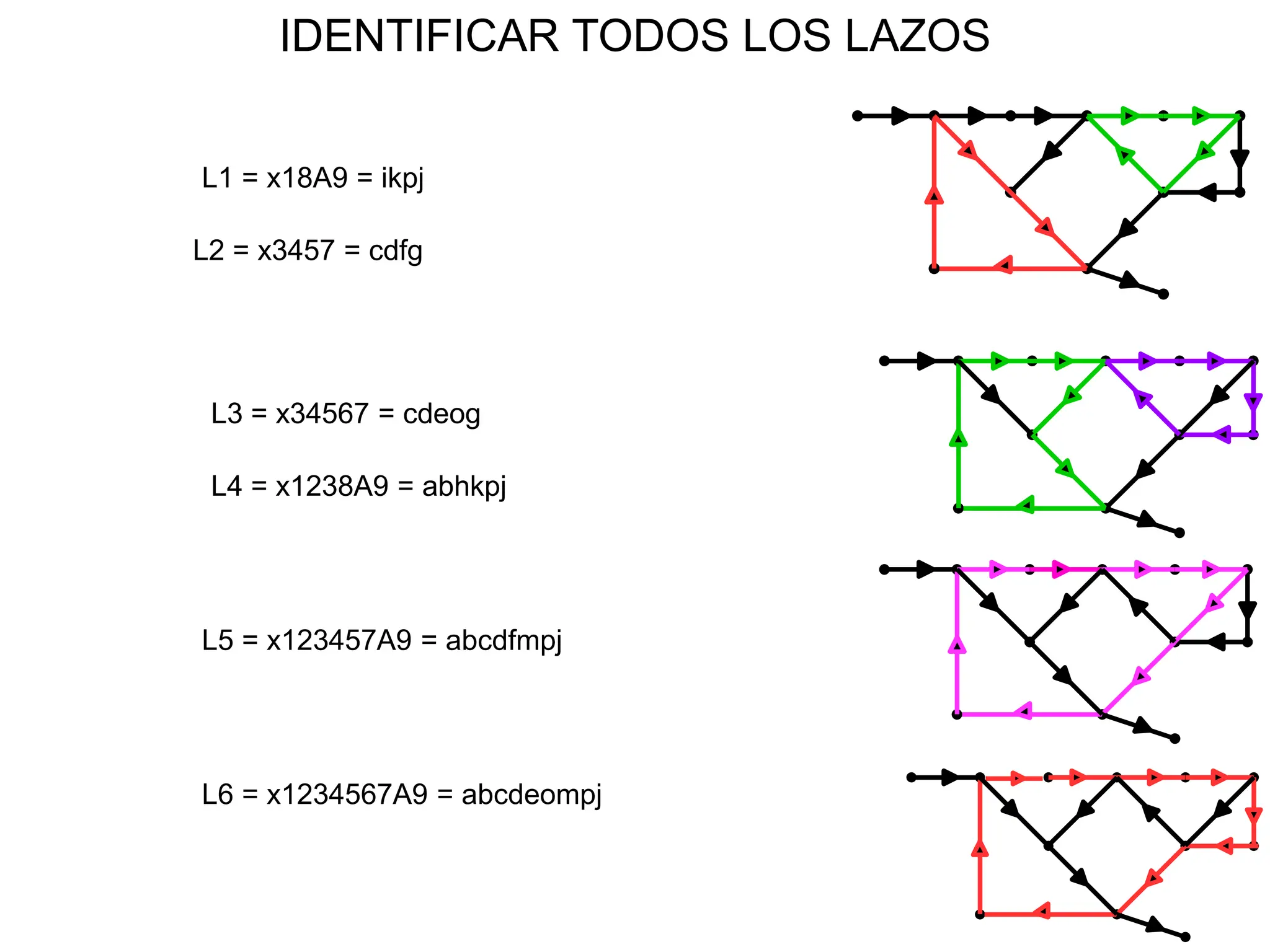
La= L1+ L2+ L3+ L4+ L5+ L6
∑
a,b
La .Lb= L1 .L2+ L1 .L3= abhkpj.cdfg+ abhkpj.cdeog
∑
a
La= abhkpj+ cdeog+ cdfg+ ikpj+ abcdfmpj+ abcdeompj
∑
a,b,c
La .Lb .Lc= no hay grupos de 3 lazos disjuntos
△T= 1− [abhkpj+ cdeog+ cdfg+ ikpj+ abcdfmpj+ abcdeompj]+
+ [abhkpj.cdfg+ abhkpj.cdeog]

10. ΔT= 1 - [abhkpj + cdeog + cdfg + ikpj + abcdfmpj + abcdeompj] + [abhkpj . cdfg + abhkpj . cdeog]
ΔT= 1 - [abhkpj + cdeog + cdfg + ikpj + abcdfmpj + abcdeompj] + [abhkpj . cdfg + abhkpj . cdeog]
Δ1 = ΔT – todo elemento de T1
T1 = i . k
Δ1= 1 - cdeog - cdfg
ΔT= 1 - [abhkpj + cdeog + cdfg + ikpj + abcdfmpj + abcdeompj] + [abhkpj . cdfg + abhkpj . cdeog]
T2 = a.b.c.d.e.o.m Δ2 = ΔT – todo elemento de T2
Δ2= 1
T3 = a.b.c.d.f.m Δ3 = ΔT – todo elemento de T3
ΔT= 1 - [abhkpj + cdeog + cdfg + ikpj + abcdfmpj + abcdeompj] + [abhkpj . cdfg + abhkpj . cdeog]
Δ3= 1
T4 = a.b.h.k Δ4 = ΔT – todo elemento de T4
ΔT= 1 - [abhkpj + cdeog + cdfg + ikpj + abcdfmpj + abcdeompj] + [abhkpj . cdfg + abhkpj . cdeog]
Δ4= 1

11. Tt=
∑
i
Ti .△i
△T
Tt = (T1. Δ1 + T2. Δ2 + T3. Δ3 + T4. Δ4) / Δ
T
Tt=
(ik)(1− cdeog− cdfg) + abcdeom+ abcdfm + abhk
1− [abhkpj+ cdeog+ cdfg+ ikpj+ abcdfmpj+ abcdeompj]+ [abhkpj.cdfg+ abhkpj.cdeog]
ΔT = 1 - [ L1 + L2 + L3 + L4 + L5 + L6 ] + [L1.L2 + L1.L3]