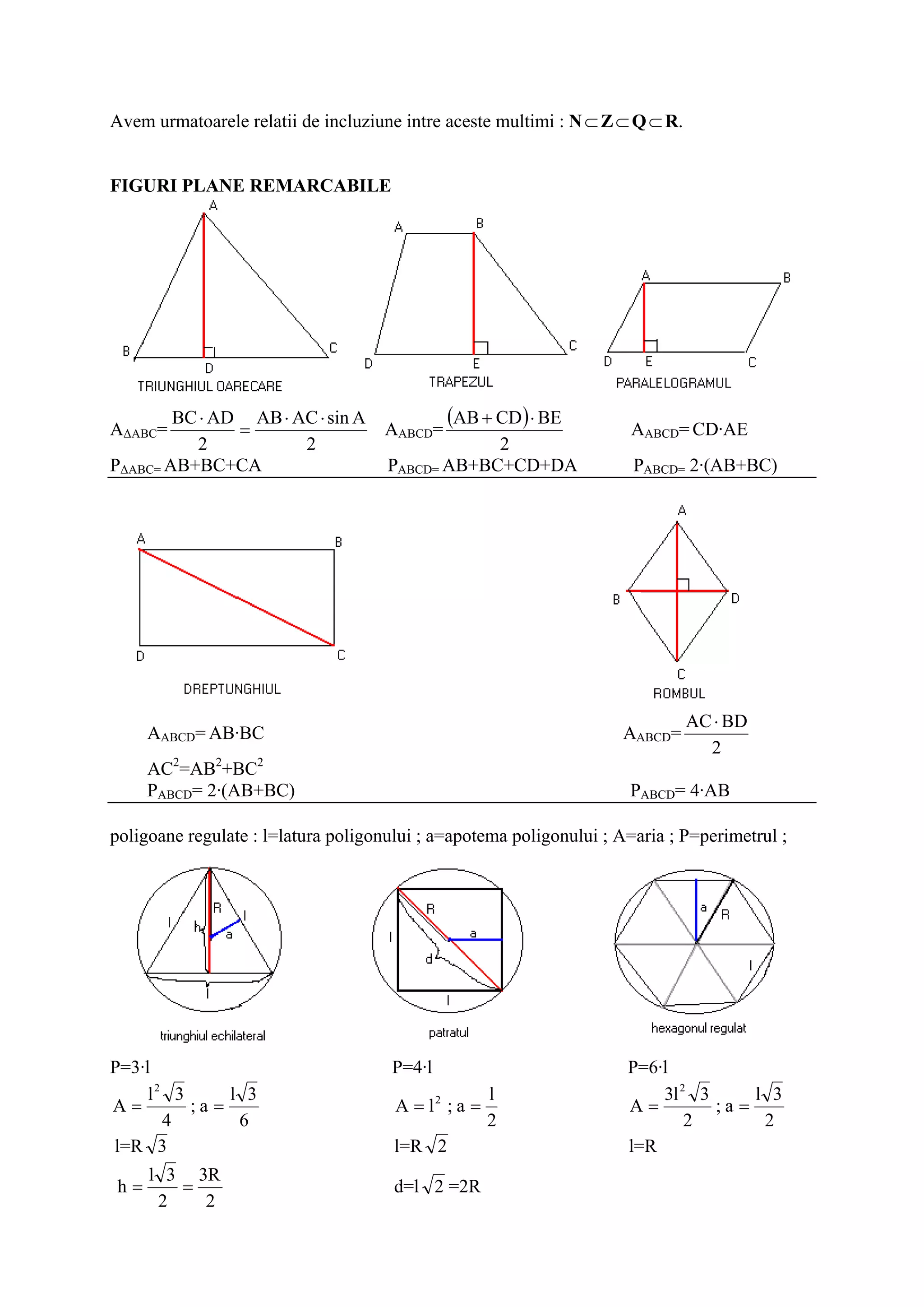
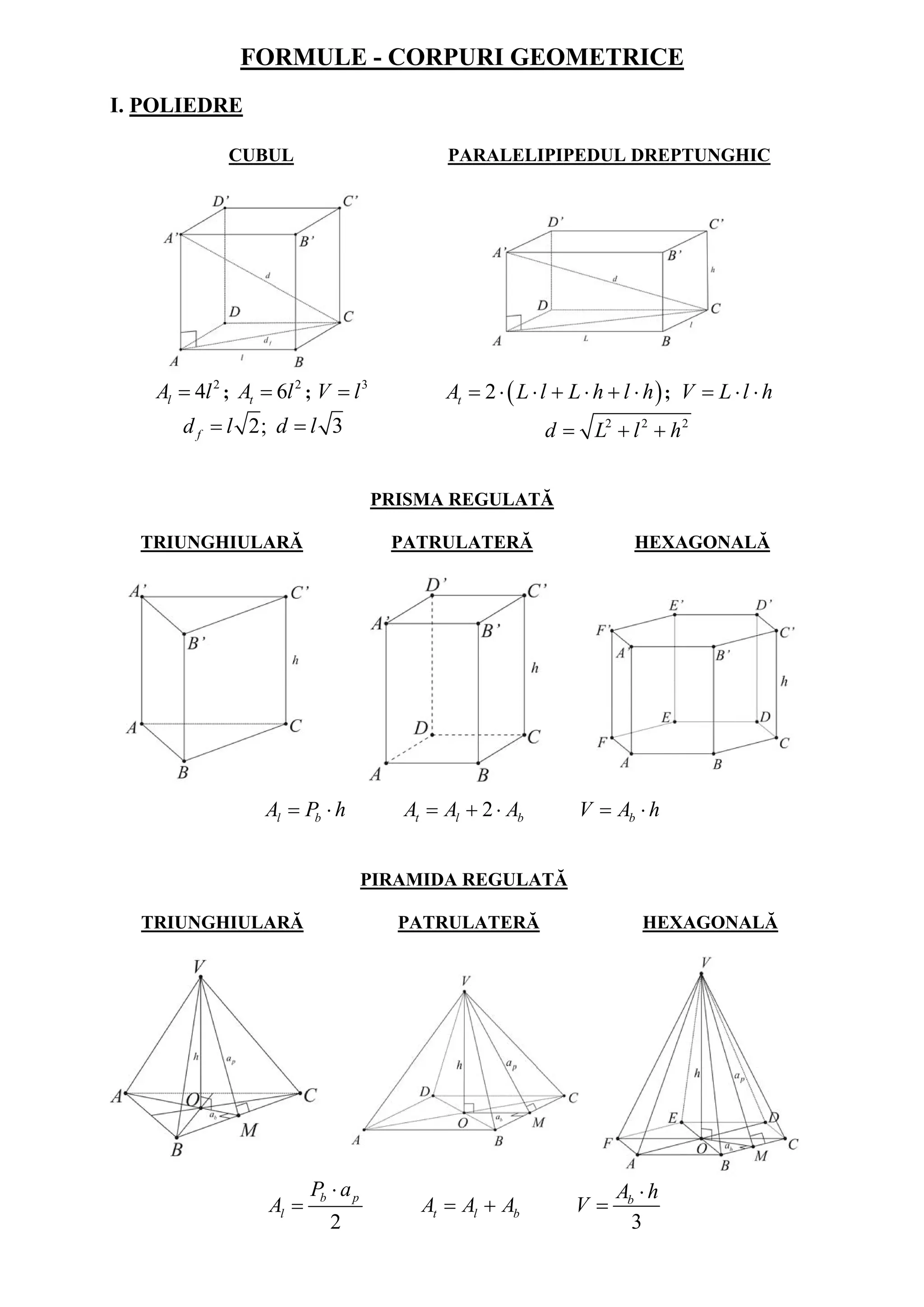
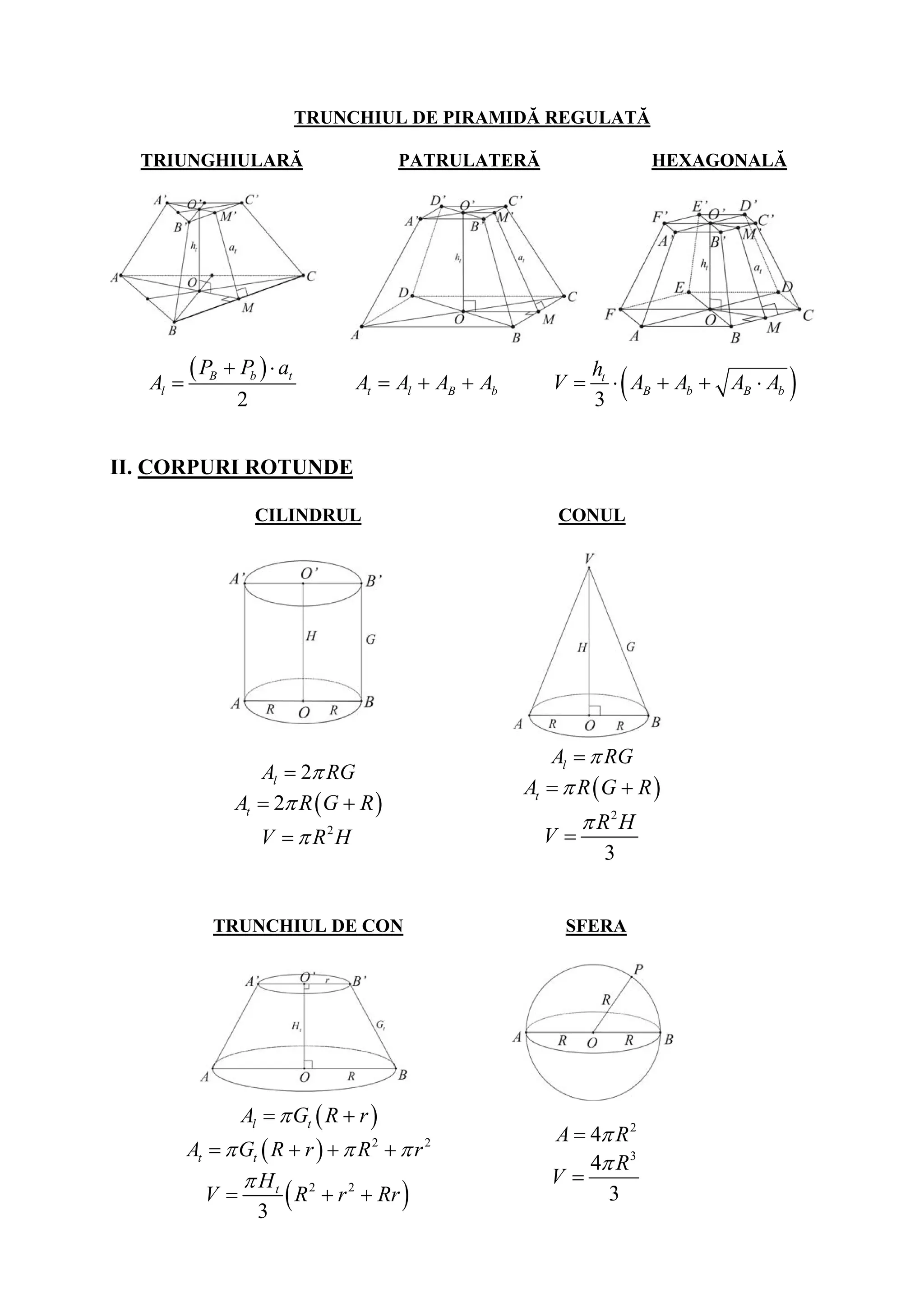
The document provides formulas for calculating expressions, properties of exponents and radicals, absolute value, linear functions, sets of numbers, plane figures, triangles, trigonometric functions, similar triangles theorem of Thales, circle, geometric solids including cube, cuboid, prism, pyramid, truncated pyramid, cylinder, cone, truncated cone and sphere.

1. FORMULE UTILE PENTRU CLASA A VIII A
www.mateinfo.ro
FORMULE DE CALCUL PRESCURTAT
(a+b)2=a2+2ab+b2 ; (a-b)2=a2-2ab+b2 ; a2-b2=(a+b)(a-b) ; (a+b+c)2=a2+b2+c2+2ab+2ac+2bc ;
(a+b)3=a3+3a2b+3ab2+b3
;
(a-b)3=a3-3a2b+3ab2-b3 ;
a3+b3=(a+b)(a2-ab+b2)
;
a3-b3=(a-b)(a2+ab+b2) ;
PROPRIETATILE PUTERILOR
an·am=an+m ; an:am=an -m ; (an)m=an·m ; (a·b)n=an·bn ; (a:b)n=an:bn ; a0=1 ; 0n=0 ; 1n=1
PROPRIETATILE RADICALILOR
a⋅b = a ⋅ b ;
a / b = a / b ; x2 = x ;
( y)
2
= y ; a≥0 ; b≥0 ; y≥0 ; exemple:
18 = 9 ⋅ 2 = 9 ⋅ 2 = 3 2 ; 5 3 = 25 ⋅ 3 = 25 ⋅ 3 = 75 ;
( 6)
(− 3)2
= −3 = 3 ;
2
= 6.
MODULUL
Definitie : |X|=X daca X≥0 si |X|= -X daca X≤0 ;
Proprietati : |X|≥0 ; |a·b|=|a|·|b| ; |a+b|≤|a|+|b| ;
Exemple : |-5|= -(-5)=5 ; |7|=7 ; |-2|= -(-2)=2 ; |+4|=4 ;
FUNCTIA LINIARA f :R R , f(x)=ax+b
P(x,y) ∈ Gf daca si numai daca f(x)=y ;
A(x,y) ∈ Gf∩ox daca f(x)=y si y=0 ;
B(x,y) ∈ Gf∩oy daca f(x)=y si x=0 ;
Daca f si g sunt doua functii atunci Q(x,y) ∈ Gf∩Gg
daca f(x)=g(x)=y ;
A(-b/a , 0) si B(0 , b)
MULTIMI DE NUMERE
Multimea numerelor naturale notata cu N : 0,1,2,3,4,…∞
Multimea numerelor intregi notata cu Z : -∞ … ,-4,-3,-2,-1,0,1,2,3,4,…+∞
Multimea numerelor rationale notata cu Q: exemple -3/4 ;5/2 ;-12/4 ;0,23 ;-5,(24) ;4,20(576) ;
Multimea numerelor reale notata cu R ; exemple : -3/4 ;5/2 ;-1/4 ; 7 5 ; − 6 ; -5,(24) ;
4,20(576) ; 0,202002000200… ;-5,2323323332333323… ;

2. Avem urmatoarele relatii de incluziune intre aceste multimi : N ⊂ Z ⊂ Q ⊂ R.
FIGURI PLANE REMARCABILE
BC ⋅ AD AB ⋅ AC ⋅ sin A
=
2
2
PΔABC= AB+BC+CA
AΔABC=
AABCD=
(AB + CD ) ⋅ BE
2
PABCD= AB+BC+CD+DA
AABCD= AB·BC
AABCD= CD·AE
PABCD= 2·(AB+BC)
AABCD=
AC2=AB2+BC2
PABCD= 2·(AB+BC)
AC ⋅ BD
2
PABCD= 4·AB
poligoane regulate : l=latura poligonului ; a=apotema poligonului ; A=aria ; P=perimetrul ;
P=3·l
l2 3
l 3
;a =
A=
4
6
l=R 3
h=
l 3 3R
=
2
2
P=4·l
A = l2 ; a =
l=R 2
d=l 2 =2R
l
2
P=6·l
3l 2 3
l 3
A=
;a =
2
2
l=R

3. TRIUNGHIUL DREPTUNGHIC
Teorema catetei:
b2=a·n
Teorema inaltimii:
c2=a·m
;
h2=m·n ;
h=
b⋅c
a
Teorema lui Pitagora: a2=b2+c2
;
c2=h2+m2 si
b⋅c a ⋅h
=
A=
2
2
Aria tr. dreptunghic:
b2=h2+n2
FUNCTII TRIGONOMETRICE
functia
45°
1
2
cos
c.o. AB
=
i.
AC
60°
sin
sin x°=
30°
3
2
3
2
1
2
2
2
2
2
cos x°=
c.a. BC
=
i.
AC
tg x°=
functia
30°
60°
45°
tg
3
3
3
1
3
3
3
1
ctg
c.o. AB
=
c.a. BC
ctg x°=
c.a. BC
=
c.o. AB
TRIUNGHIURI ASEMENEA ,TEOREMA LUI THALES
rezulta:
AB AC BC
=
=
MN MP NP
rezulta:
AB AC
=
AM AN
CERCUL
Lc= 2π R ;
Ac= π R 2 ;
Daca m ∠AOB = x o atunci :
π Rx o
LAB=
180 o
πR 2xo
AOAB=
360 o

4. www.mateinfo.ro
FORMULE - CORPURI GEOMETRICE
I. POLIEDRE
CUBUL
PARALELIPIPEDUL DREPTUNGHIC
Al = 4l 2 ; At = 6l 2 ; V = l 3
At = 2 ⋅ ( L ⋅ l + L ⋅ h + l ⋅ h ) ; V = L ⋅ l ⋅ h
d f = l 2; d = l 3
d = L2 + l 2 + h 2
PRISMA REGULATĂ
TRIUNGHIULARĂ
PATRULATERĂ
Al = Pb ⋅ h
At = Al + 2 ⋅ Ab
HEXAGONALĂ
V = Ab ⋅ h
PIRAMIDA REGULATĂ
TRIUNGHIULARĂ
Al =
PATRULATERĂ
Pb ⋅ a p
2
At = Al + Ab
HEXAGONALĂ
V=
Ab ⋅ h
3

5. www.mateinfo.ro
TRUNCHIUL DE PIRAMIDĂ REGULATĂ
TRIUNGHIULARĂ
Al =
PATRULATERĂ
( PB + Pb ) ⋅ at
At = Al + AB + Ab
2
HEXAGONALĂ
V=
(
ht
⋅ AB + Ab + AB ⋅ Ab
3
II. CORPURI ROTUNDE
CILINDRUL
CONUL
Al = π RG
At = π R ( G + R )
Al = 2π RG
At = 2π R ( G + R )
V=
V =πR H
2
TRUNCHIUL DE CON
At = π Gt ( R + r ) + π R + π r
π Ht 2 2
V=
( R + r + Rr )
3
3
SFERA
Al = π Gt ( R + r )
2
π R2 H
2
A = 4π R 2
4π R 3
V=
3
)