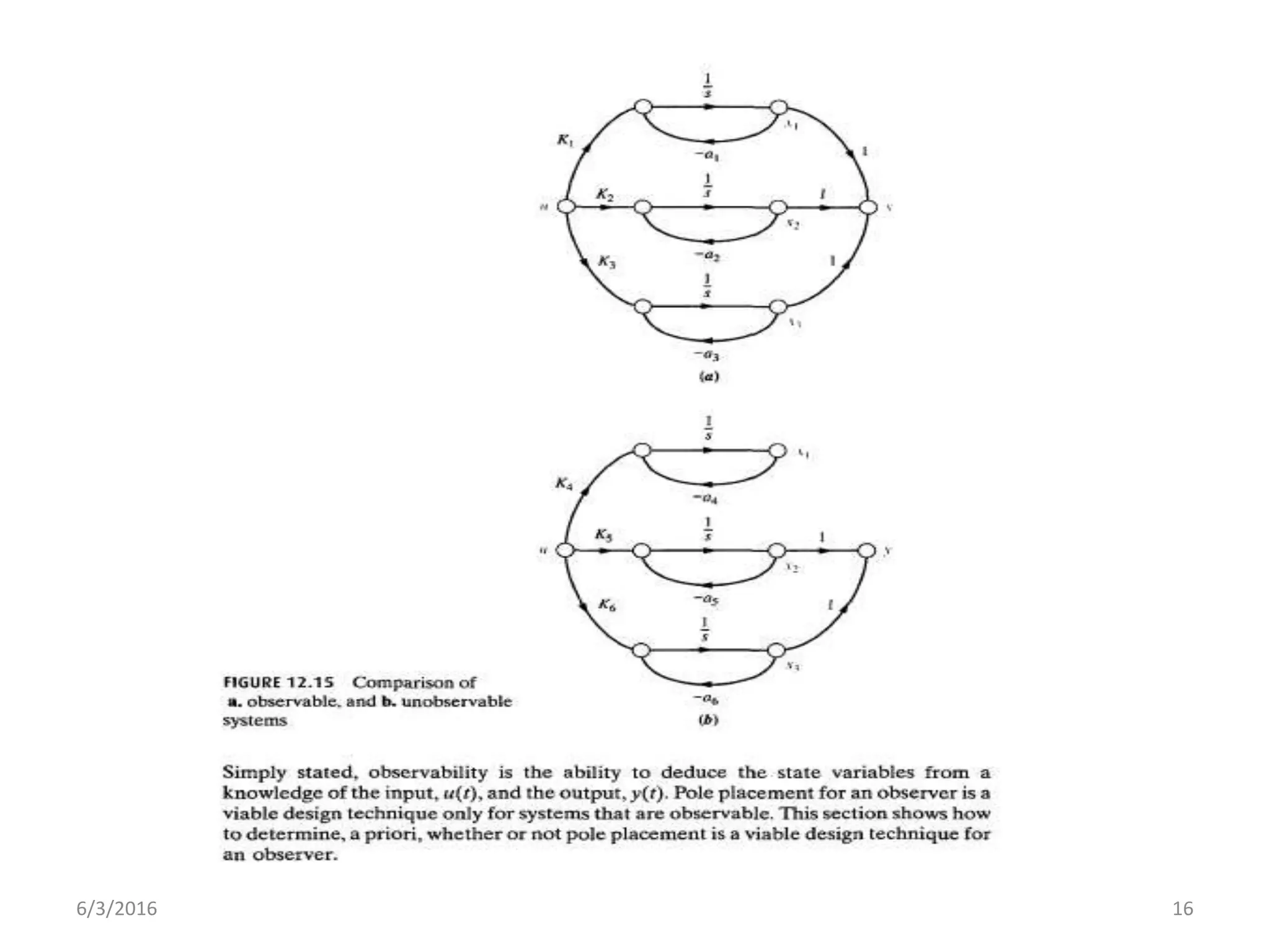
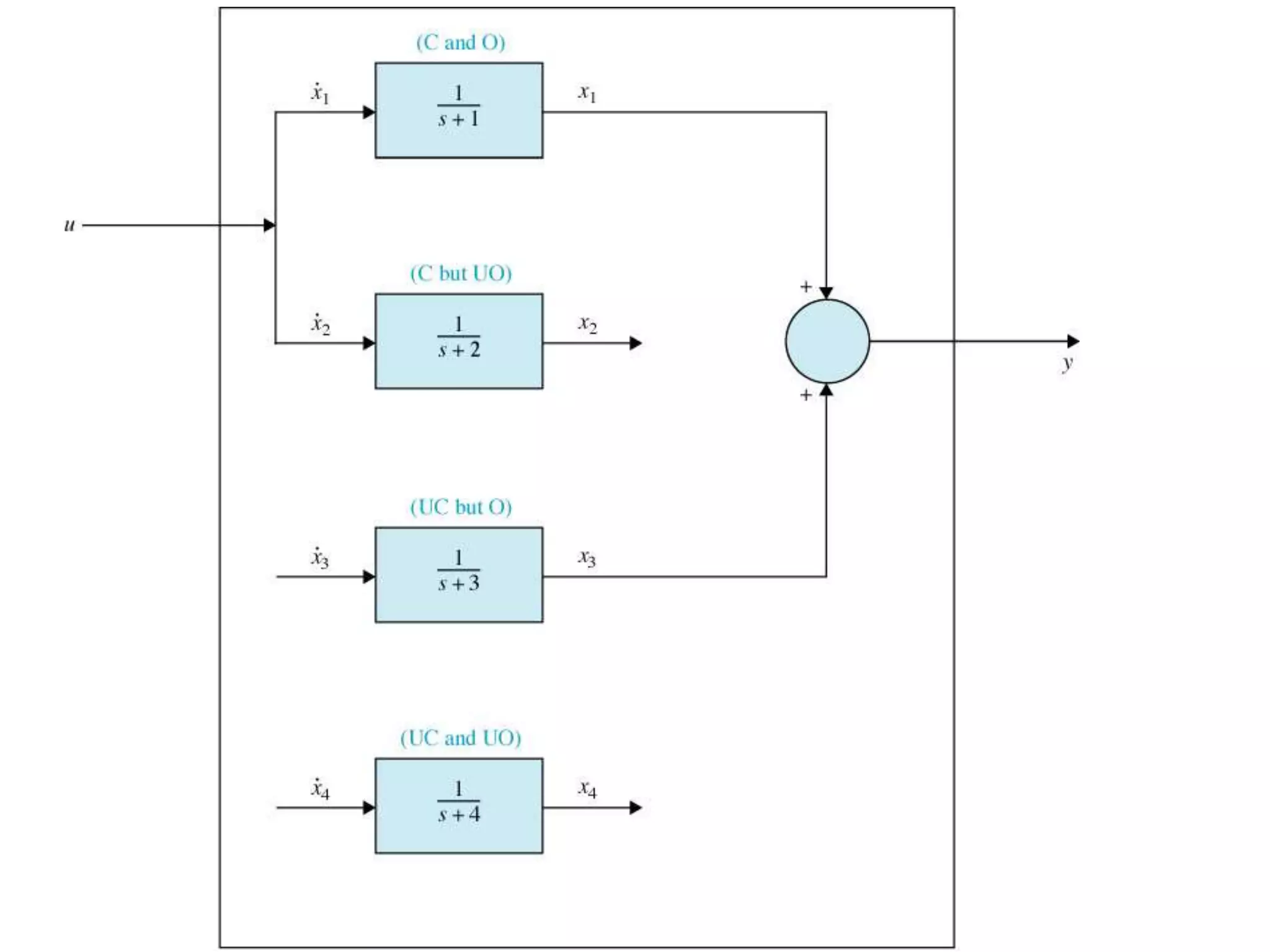
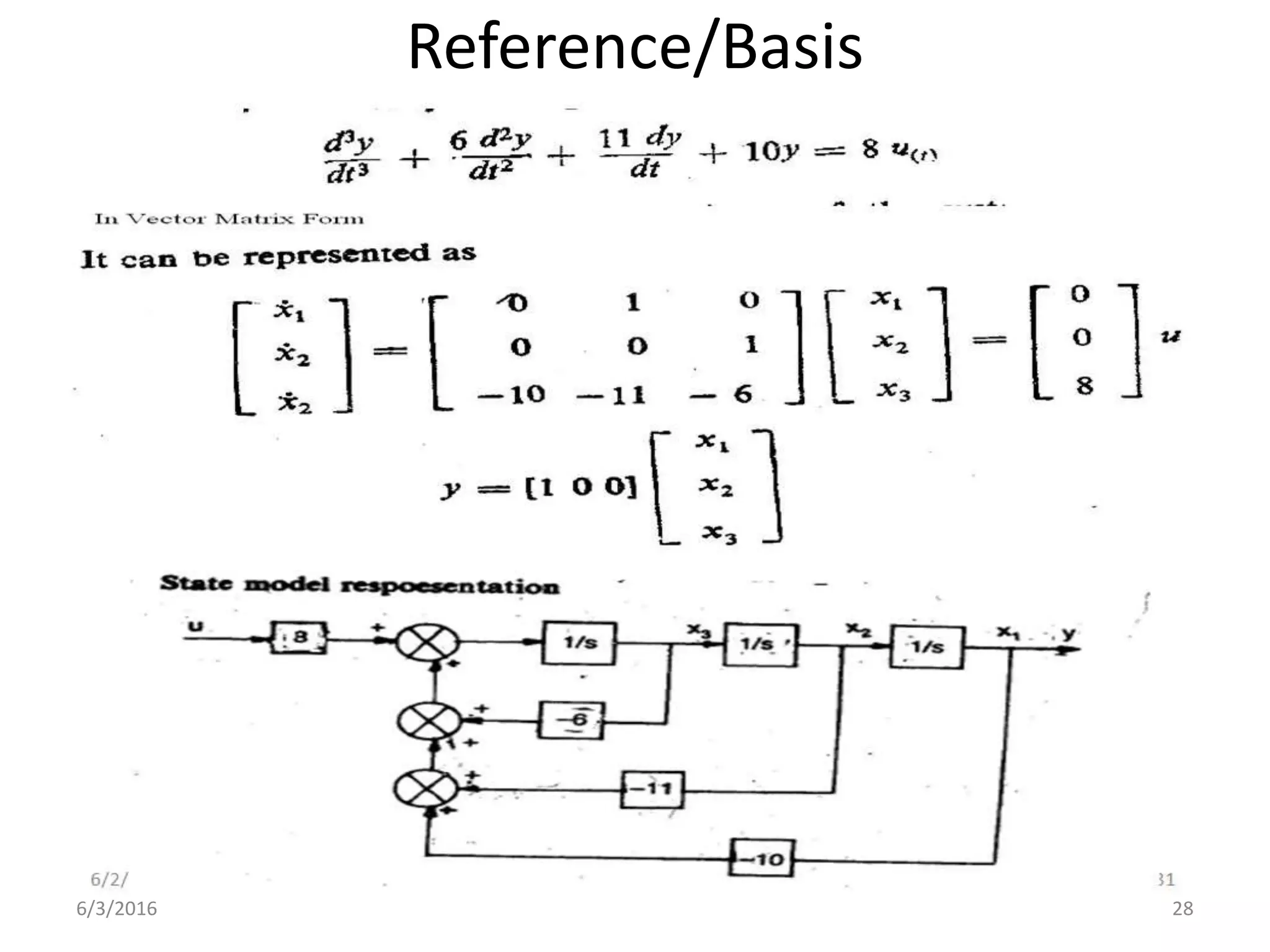
This document discusses controllability and observability of systems using Matlab. It provides an example of checking the controllability and observability of a 2nd order system. The controllability and observability matrices are calculated from the state space matrices using Matlab functions. The rank of each matrix is then checked to determine if the system is controllable/observable or not.




































![• % State Space Representation % x' = Ax + Bu % y = Cx + Du % %
Problem 1 --------------------------------------------------------------- %
• Check Controllability and Observability of a 2nd order System %
• Given ------------------------------------------------------------------- MatrixA =
[0 1;-2 -3]; MatrixB = [0;1]; MatrixC = [1 -1]; MatrixD = 0; %
• Objective --------------------------------------------------------------- %
• 1) To Find Controllable Matrix Qc, its rank and check controllability
• % 2) To Find Observable Matrix Qb, its rank and check observability
%------
• --- % Controllable Matrix -----------------------------------------------------
Qc = ctrb(MatrixA,MatrixB); rankQc = rank(Qc); disp('Controllable
Matrix is Qc = '); disp(Qc); if(rankQc == rank(MatrixA)) disp('Given
System is Controllable.'); else disp('Given System is Uncontrollable');
end % Observable Matrix -------------------------------------------------------
Qb = obsv(MatrixA, MatrixC); rankQb = rank(Qb); disp('Observable
Matrix is Qb = '); disp(Qb); if(rankQb == rank(MatrixA)) disp('Given
System is Observable.'); else disp('Given System is Unobservable');
end % End of Program ----------------](https://image.slidesharecdn.com/week16controllabilityandobservabilityjune1final-160603092314/75/Week-16-controllability-and-observability-june-1-final-49-2048.jpg)



