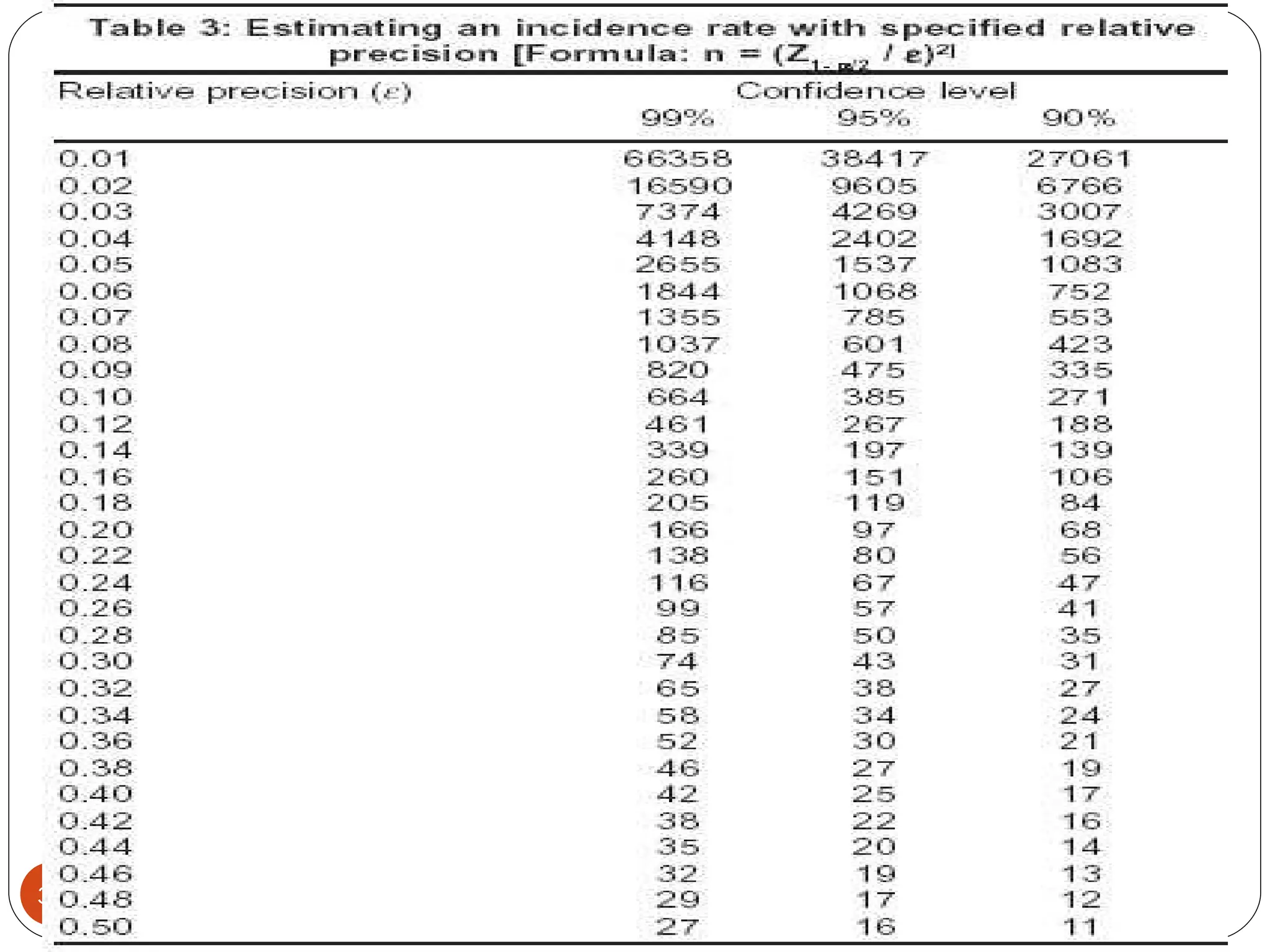
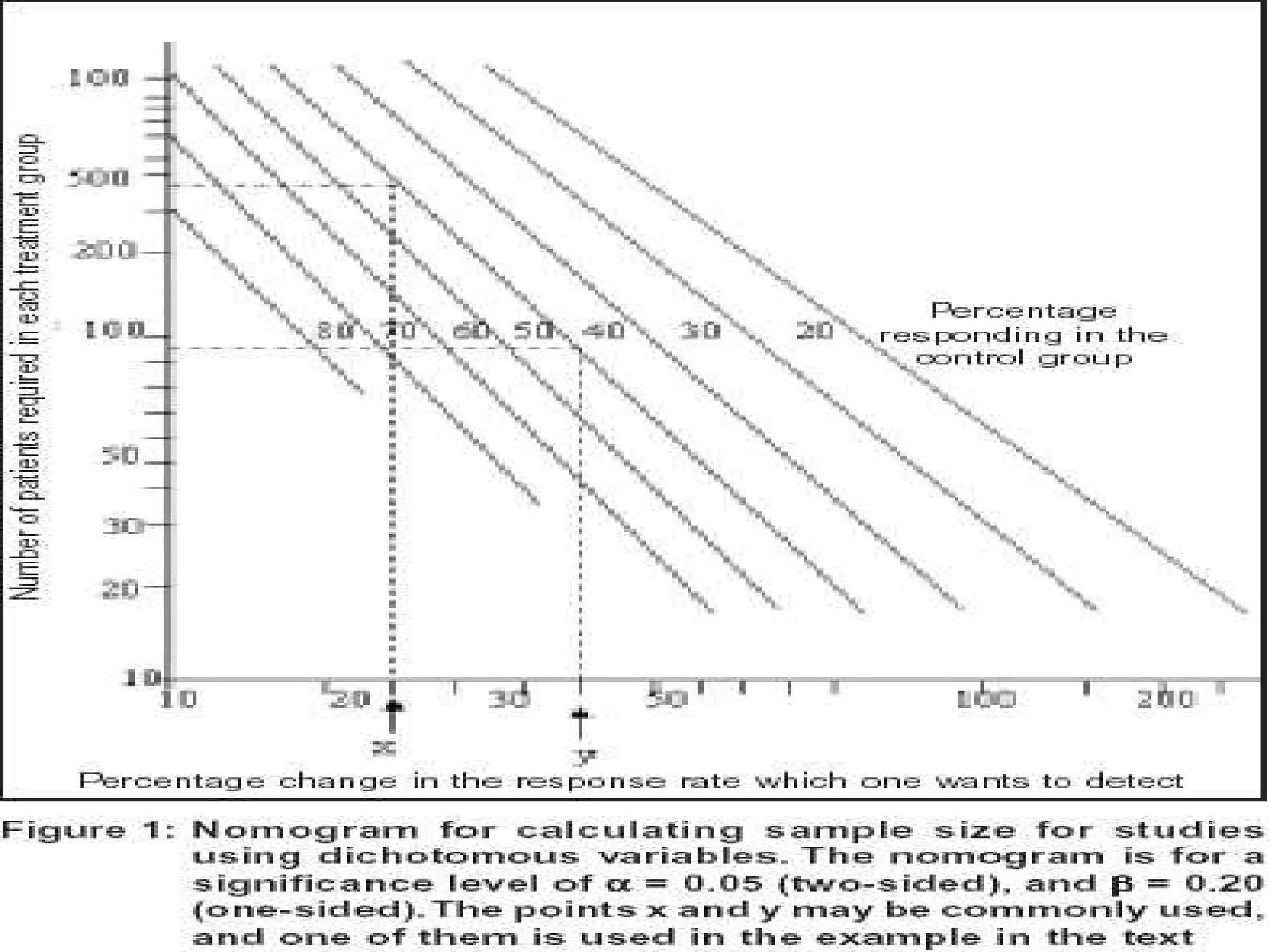
This document provides an outline for a presentation on determining sample size. It discusses key concepts like what sample size is, why determining an appropriate sample size is important, and factors that affect sample size calculations like available resources, required accuracy, and study design. The presentation aims to help audiences understand how to determine sample sizes and how to apply the concept in research and studies.