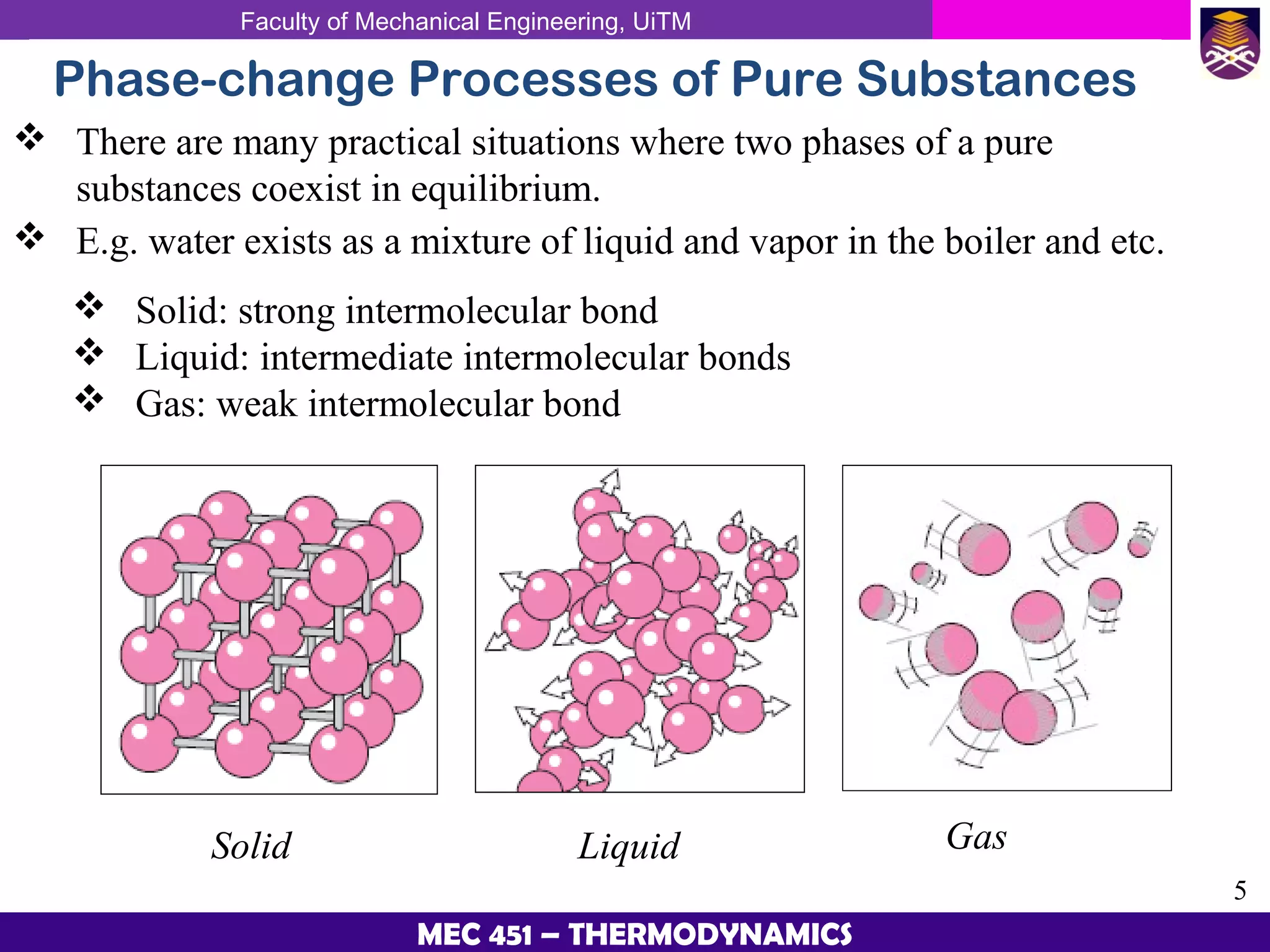
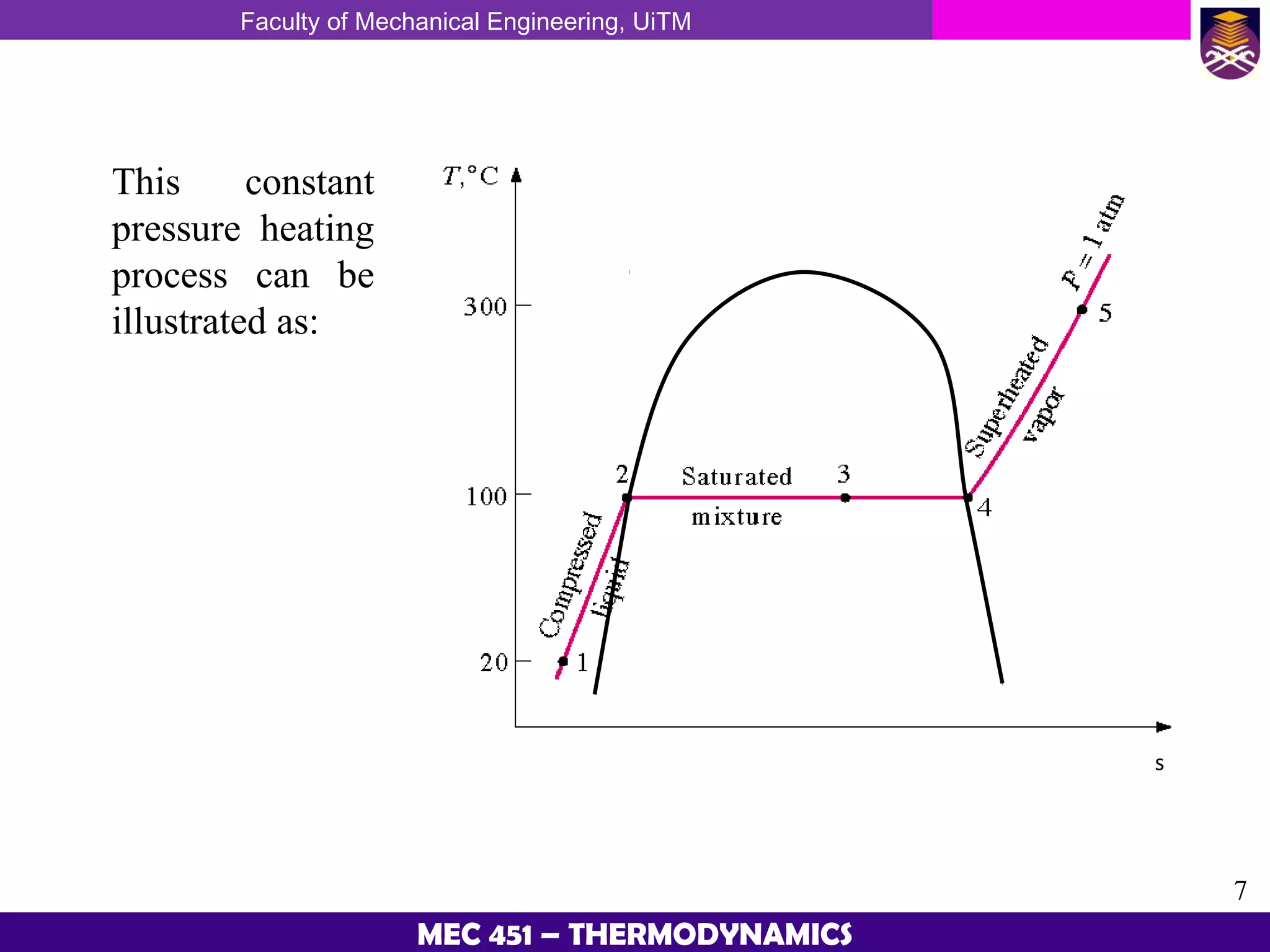
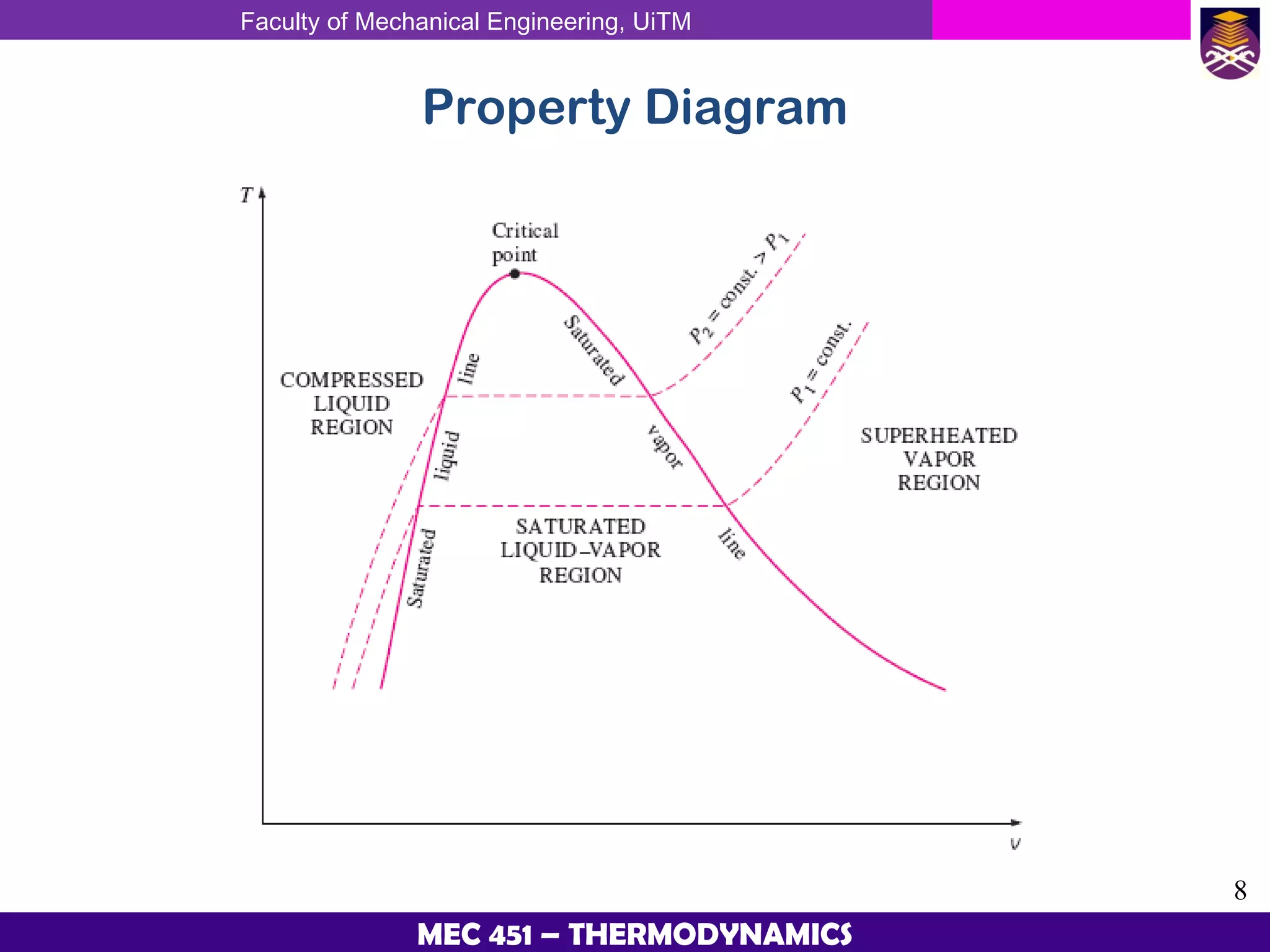
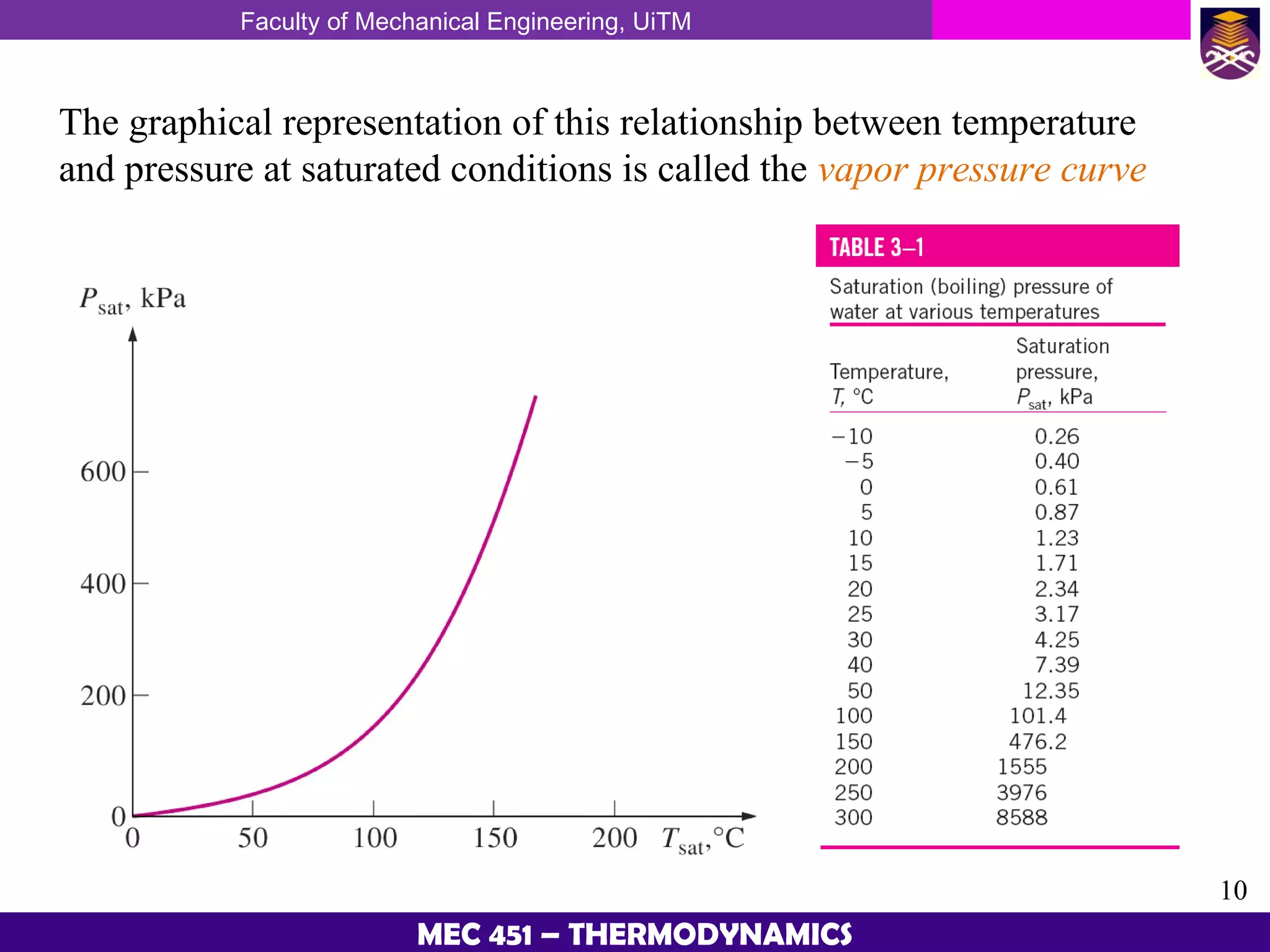
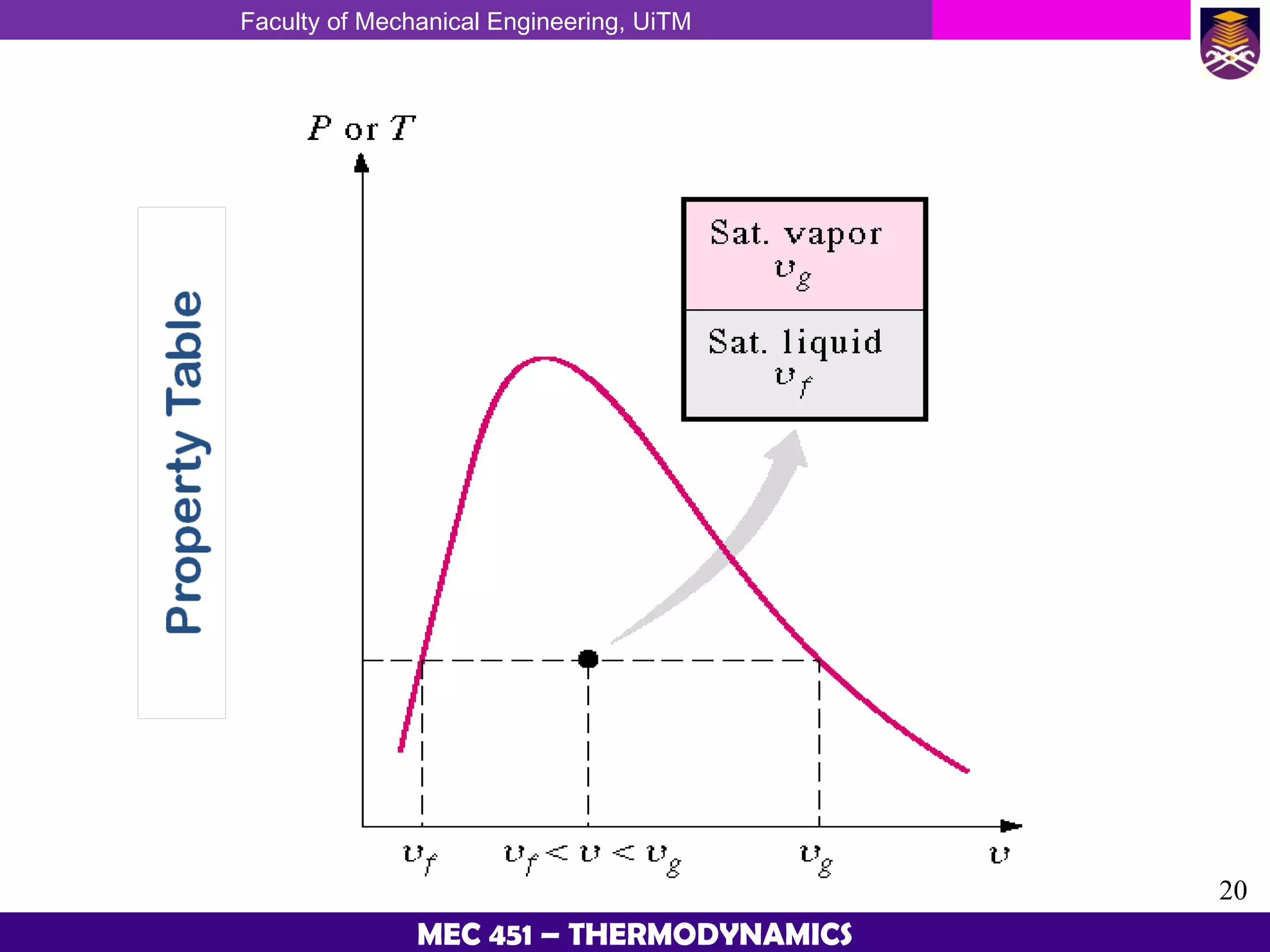
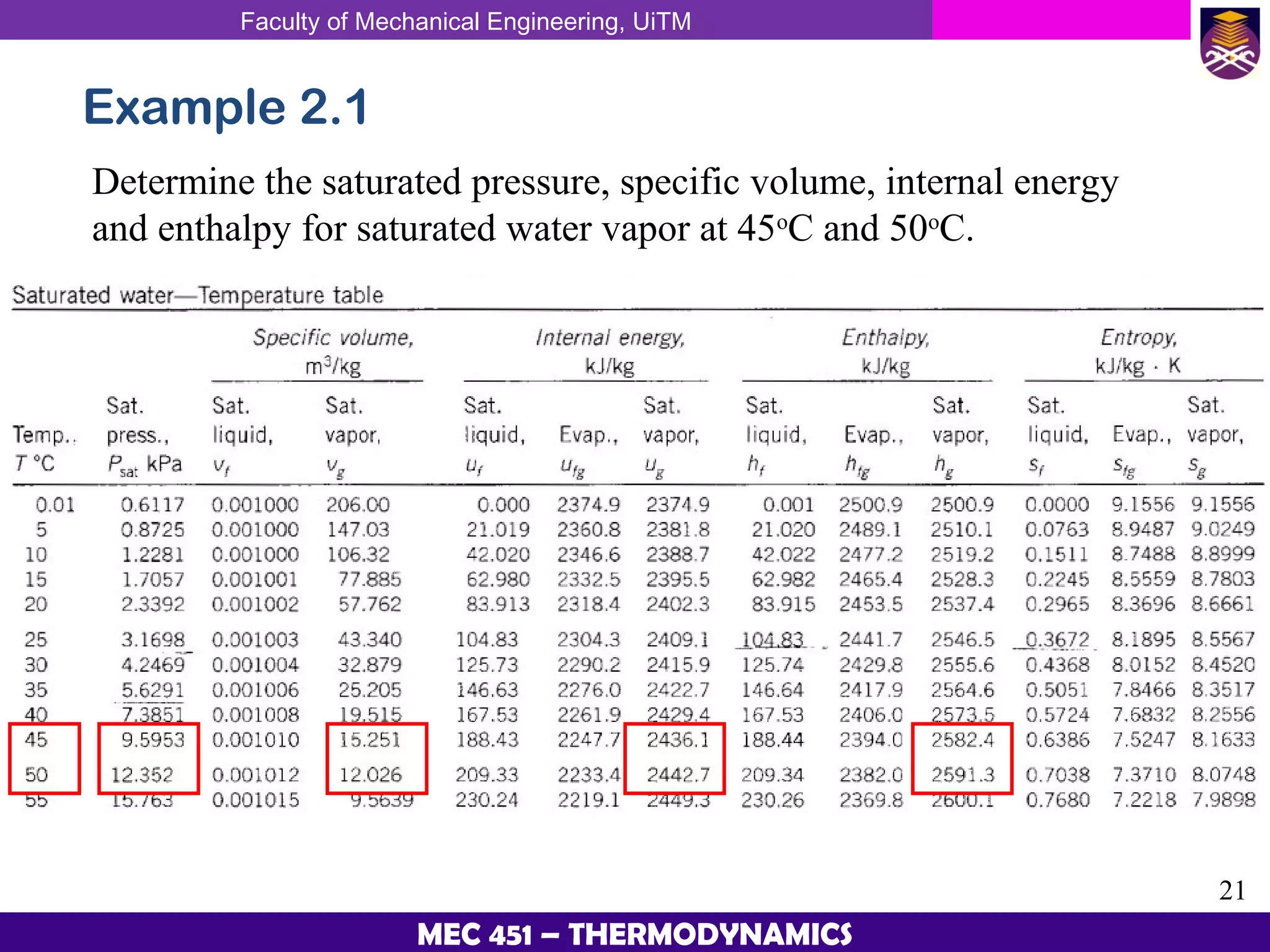
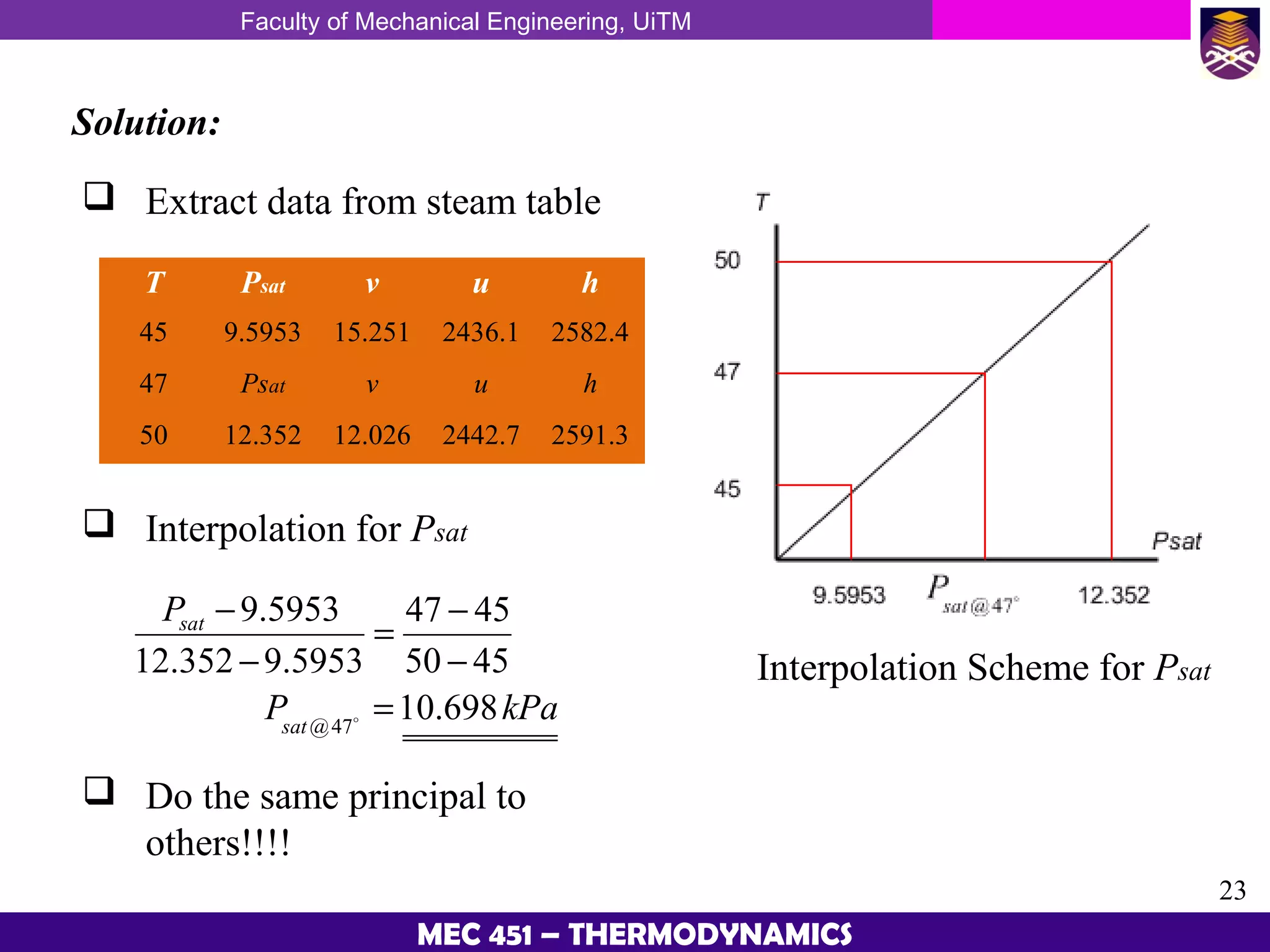
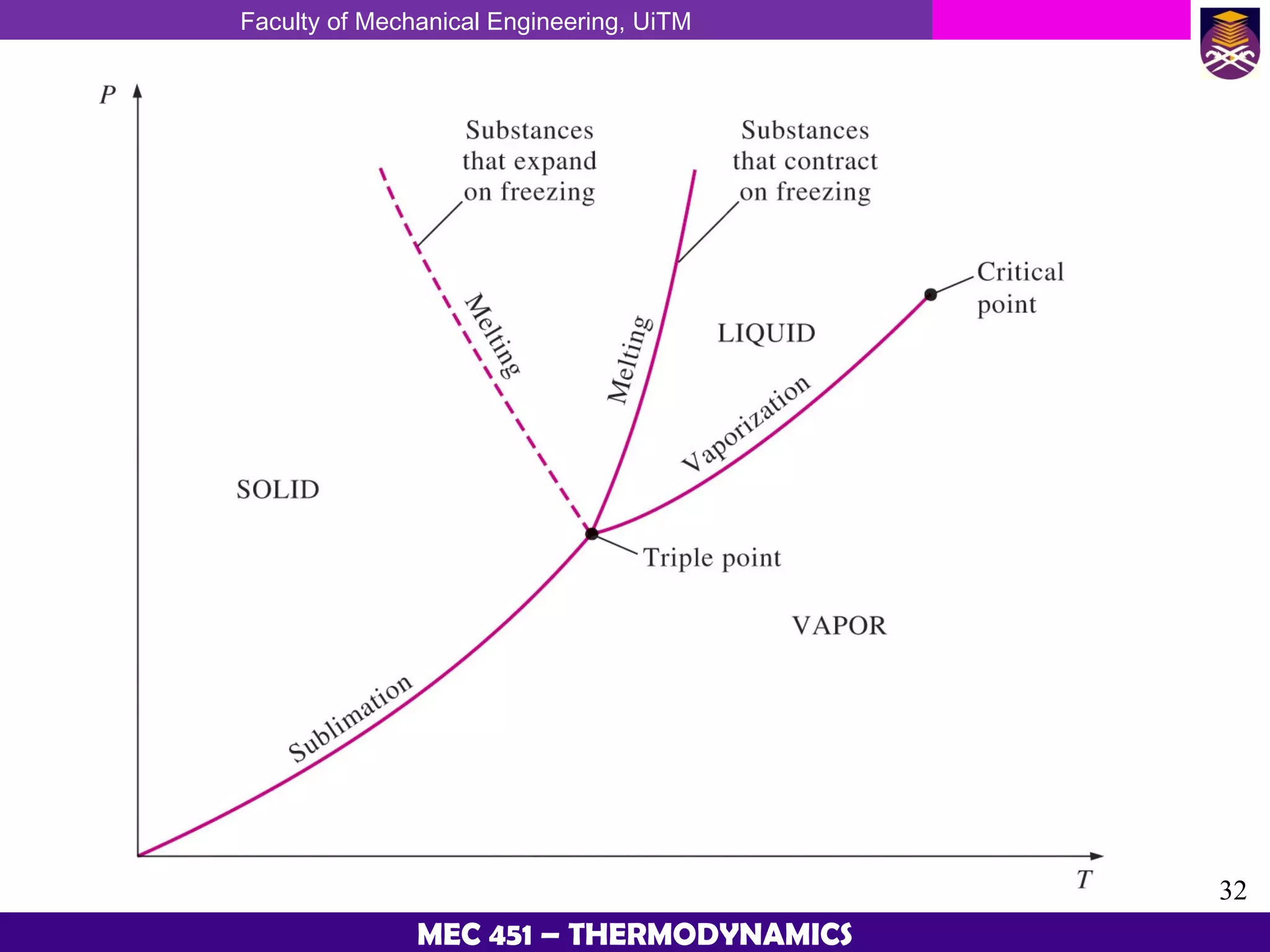
This document provides an overview of properties of pure substances and phase change processes. It defines a pure substance as having a fixed chemical composition throughout. Pure substances can exist in solid, liquid, or gas phases. Phase change processes like melting, boiling, and condensation occur at saturation conditions where two phases coexist in equilibrium. Properties like specific volume, internal energy, and enthalpy vary based on temperature, pressure, and quality (ratio of vapor mass to total mass) of mixtures. Property tables and interpolation are used to determine properties at given conditions for pure substances like water. Examples show how to apply these concepts to calculate properties like pressure, temperature, and enthalpy at different states.