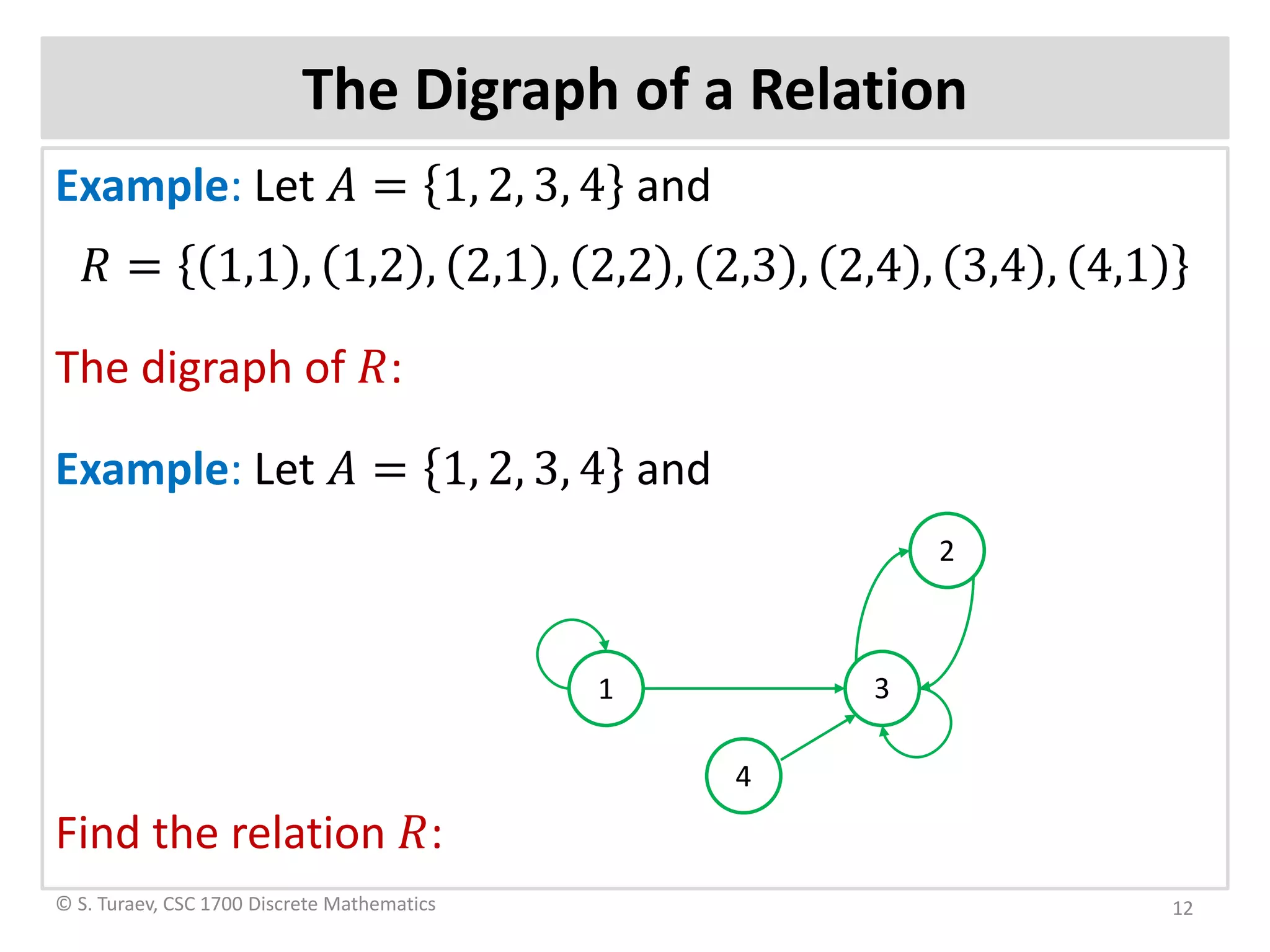
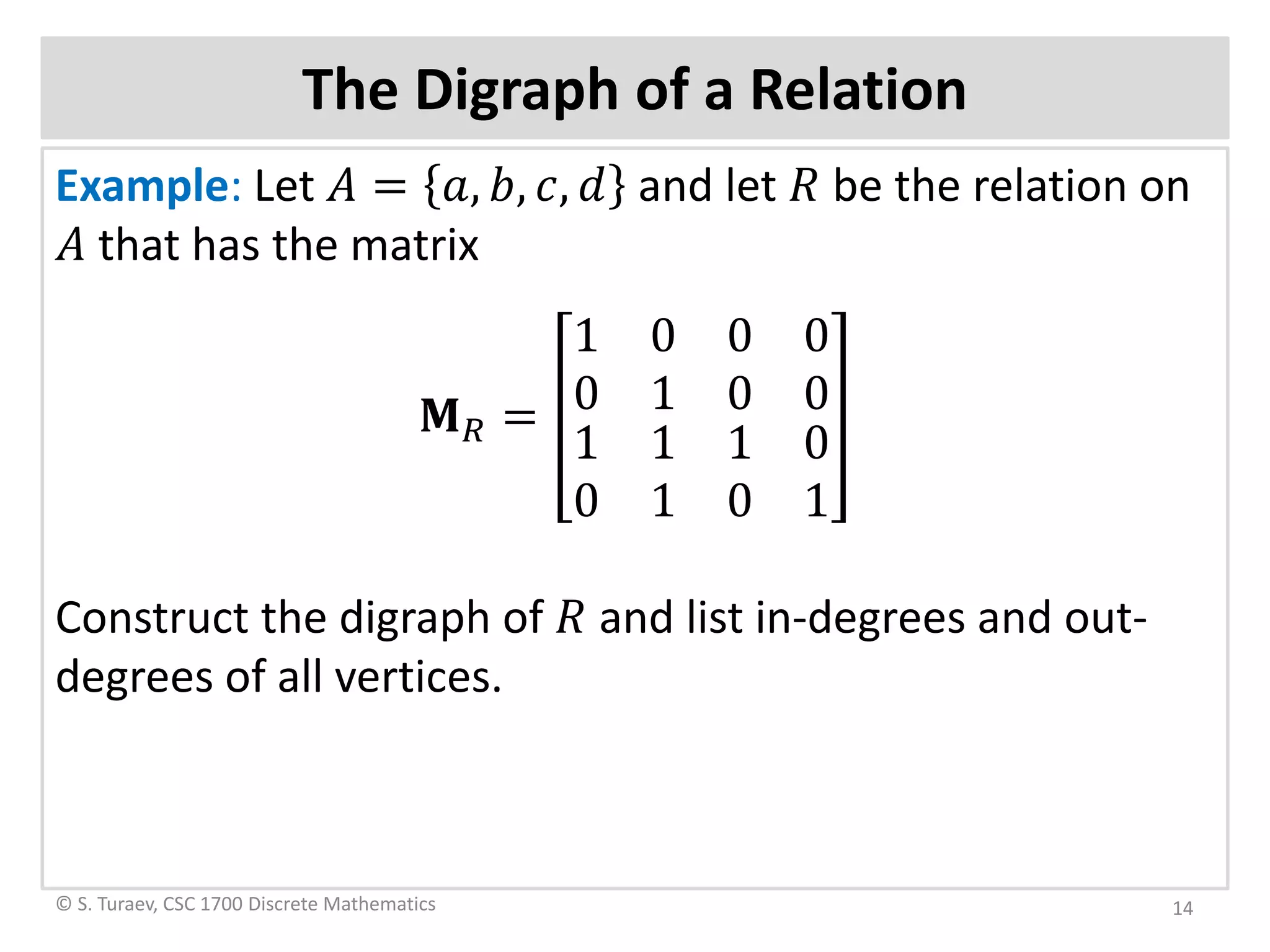
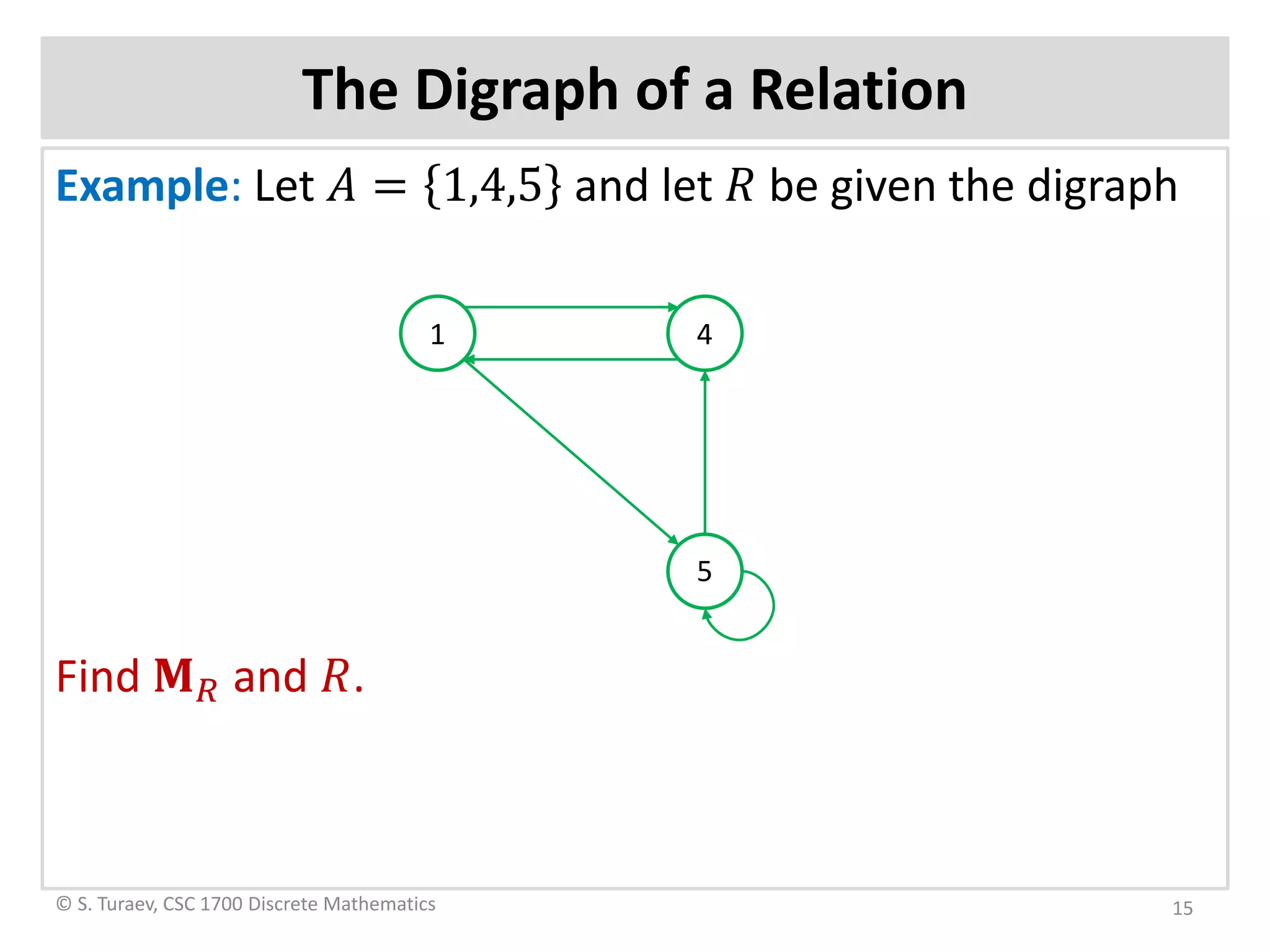
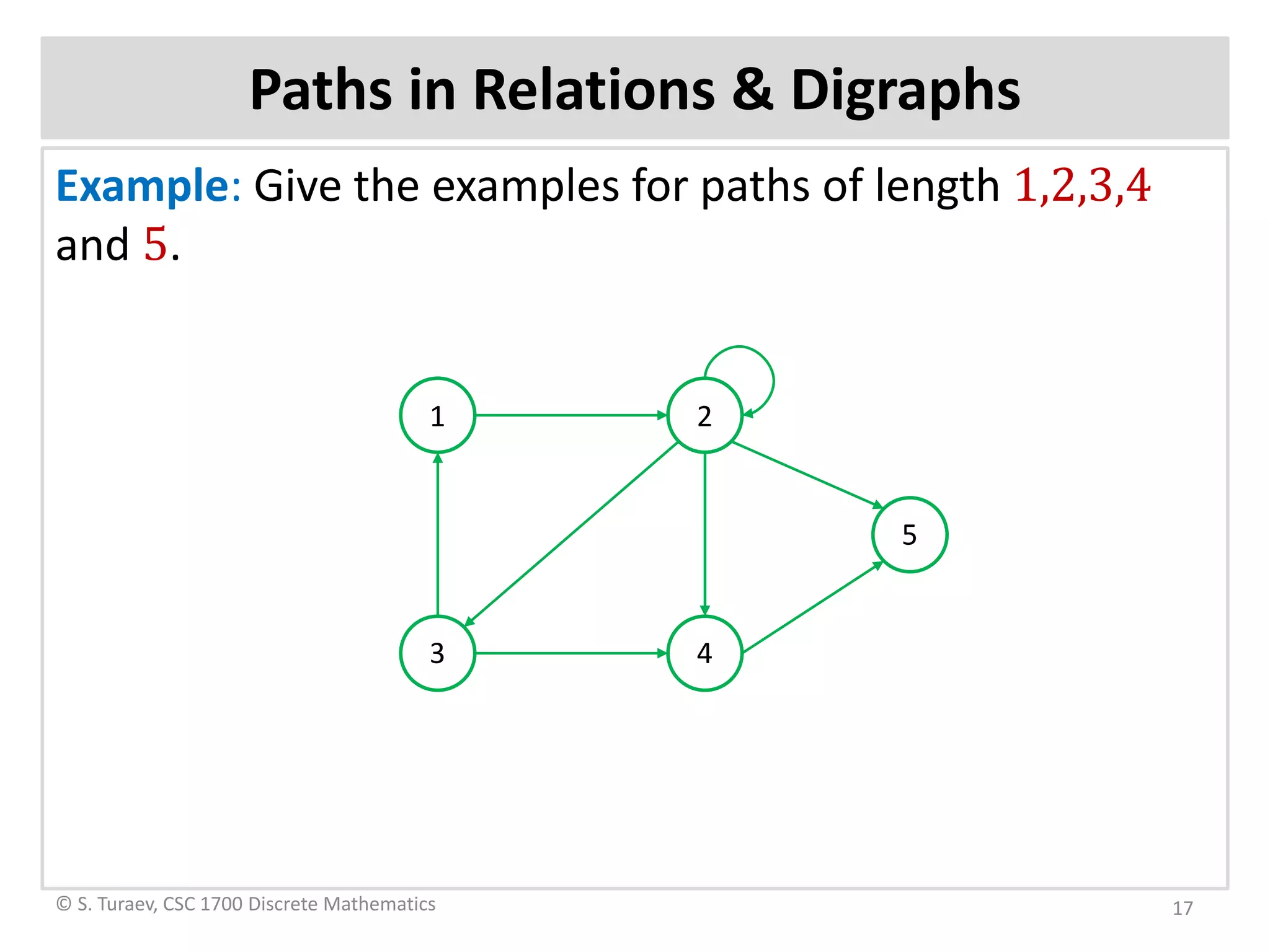
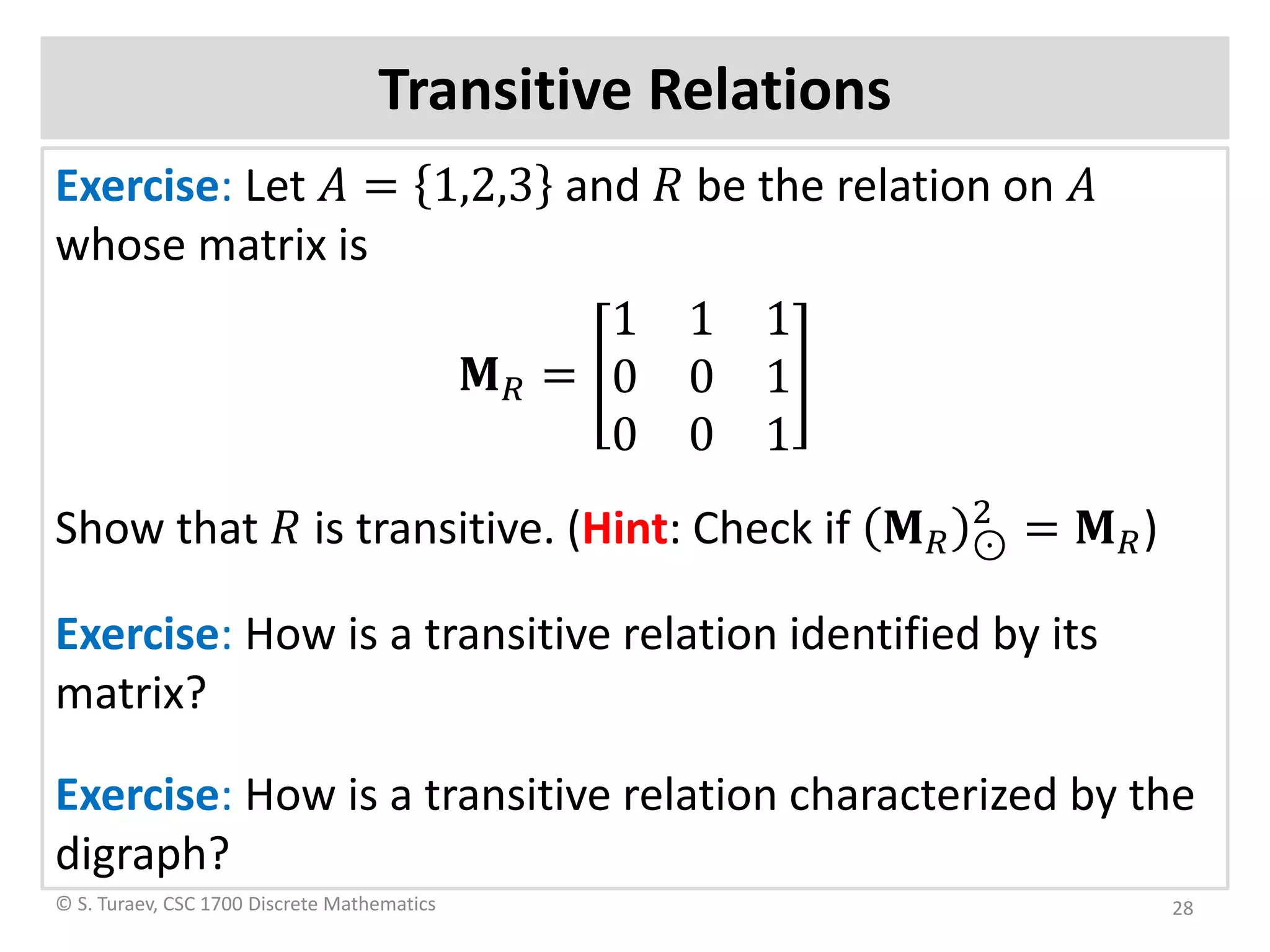
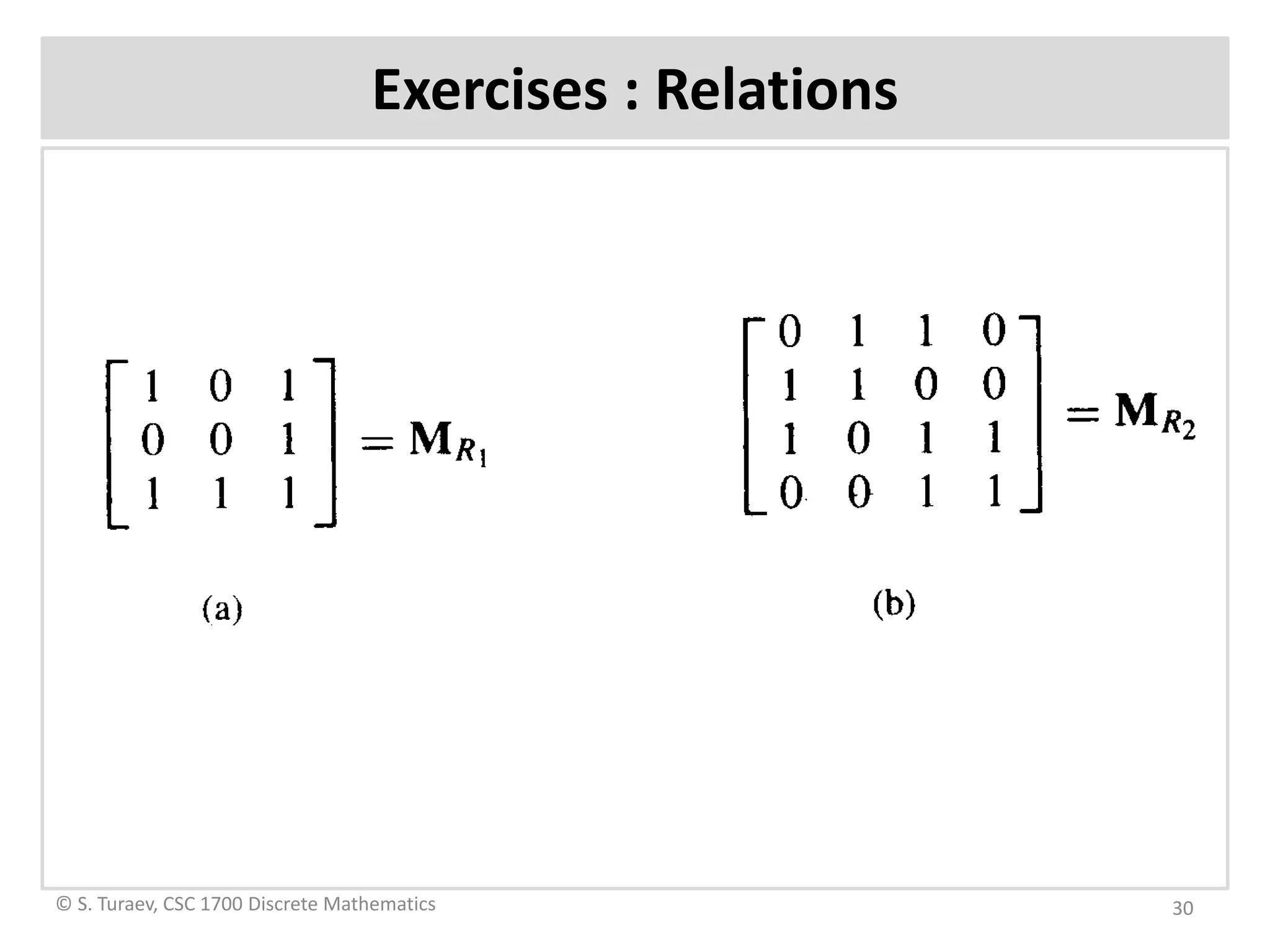
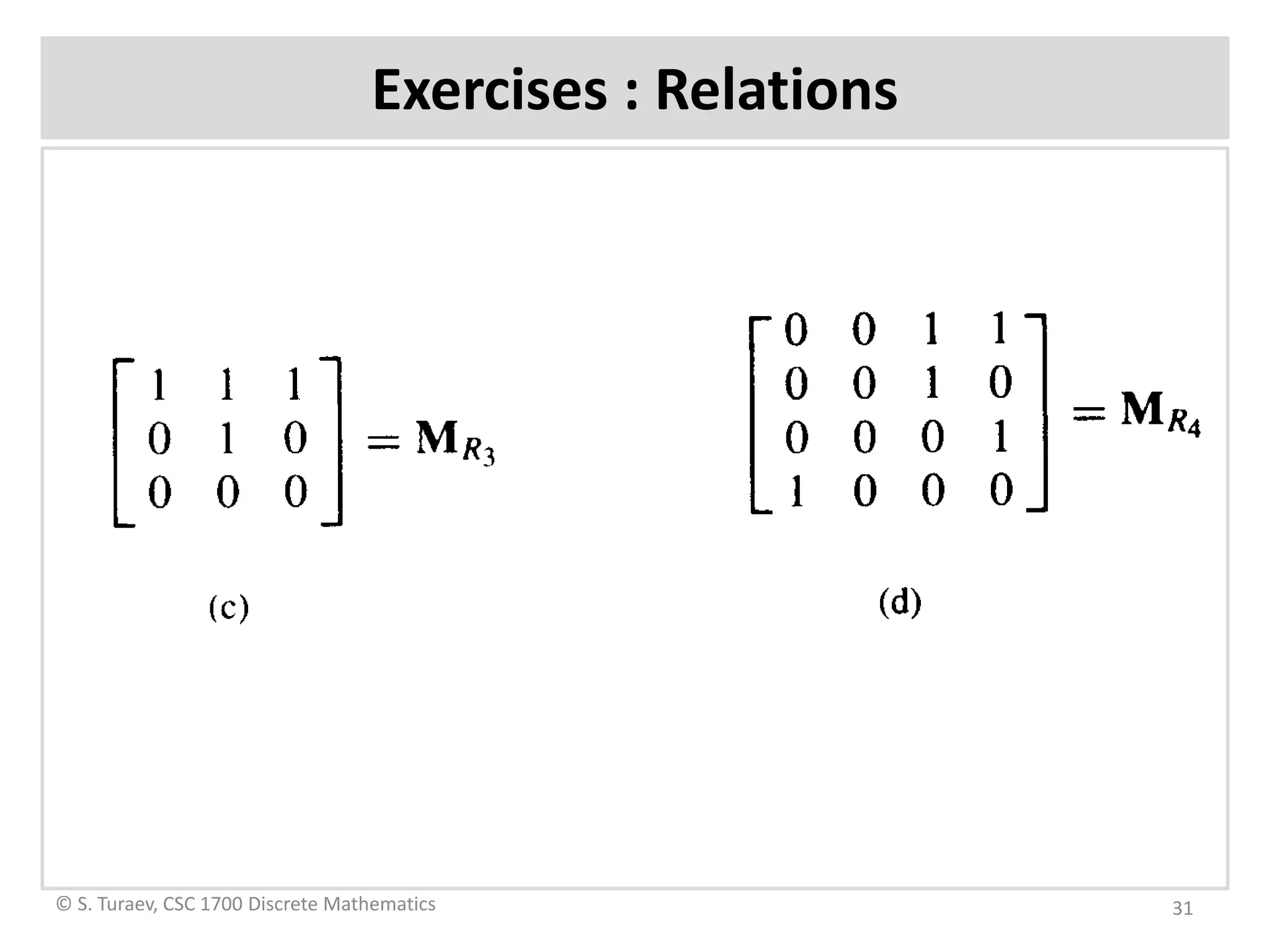
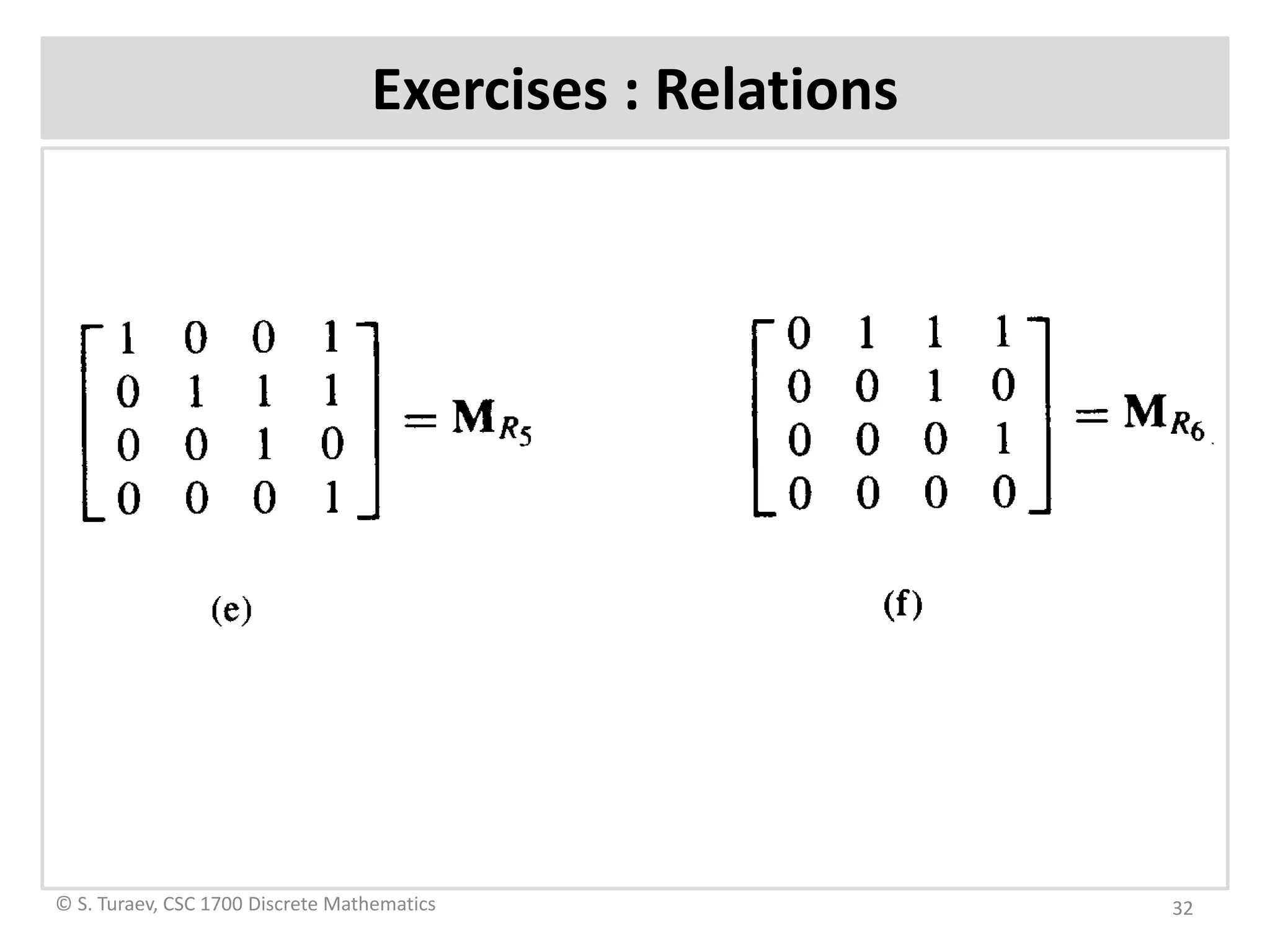
The document defines ordered pairs, product sets, relations, and digraphs. It provides examples of defining relations between sets and representing them using matrices and digraphs. It introduces concepts such as the domain and range of a relation. It also describes paths in relations and digraphs, and how to compute higher powers of the relation matrix to determine connectivity between elements.









![The Matrix of a Relation
Definition: Let 𝐴𝐴 = 𝑎𝑎1, 𝑎𝑎2, … , 𝑎𝑎 𝑚𝑚 , 𝐵𝐵 = 𝑏𝑏1, 𝑏𝑏2, … , 𝑏𝑏𝑛𝑛
and 𝑅𝑅 ⊆ 𝐴𝐴 × 𝐵𝐵 be a relation. We represent 𝑅𝑅 by the 𝑚𝑚 ×
𝑛𝑛 matrix 𝐌𝐌𝑅𝑅 = [𝑚𝑚𝑖𝑖𝑖𝑖], which is defined by
𝑚𝑚𝑖𝑖𝑖𝑖 = �
1, 𝑎𝑎𝑖𝑖, 𝑏𝑏𝑗𝑗 ∈ 𝑅𝑅
0, 𝑎𝑎𝑖𝑖, 𝑏𝑏𝑗𝑗 ∉ 𝑅𝑅
The matrix 𝐌𝐌𝑅𝑅 is called the matrix of 𝑅𝑅.
Example: Let 𝐴𝐴 = 1,2,3 and 𝐵𝐵 = 𝑟𝑟, 𝑠𝑠 .
𝑅𝑅 = 1, 𝑟𝑟 , 2, 𝑠𝑠 , 3, 𝑟𝑟 𝐌𝐌𝑅𝑅 =
© S. Turaev, CSC 1700 Discrete Mathematics 10](https://image.slidesharecdn.com/relationsdigraphs-150305012139-conversion-gate01/75/Relations-digraphs-10-2048.jpg)