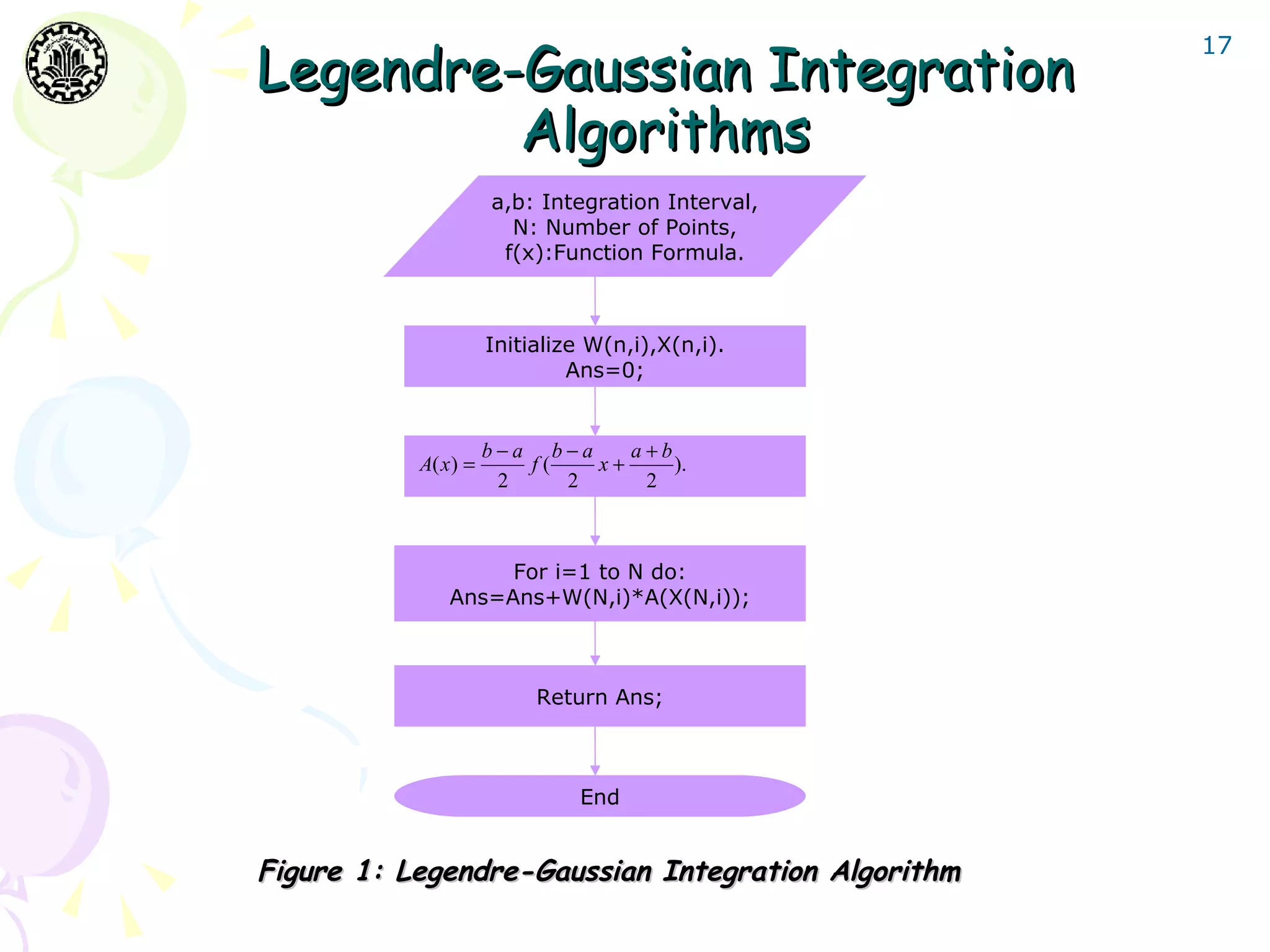
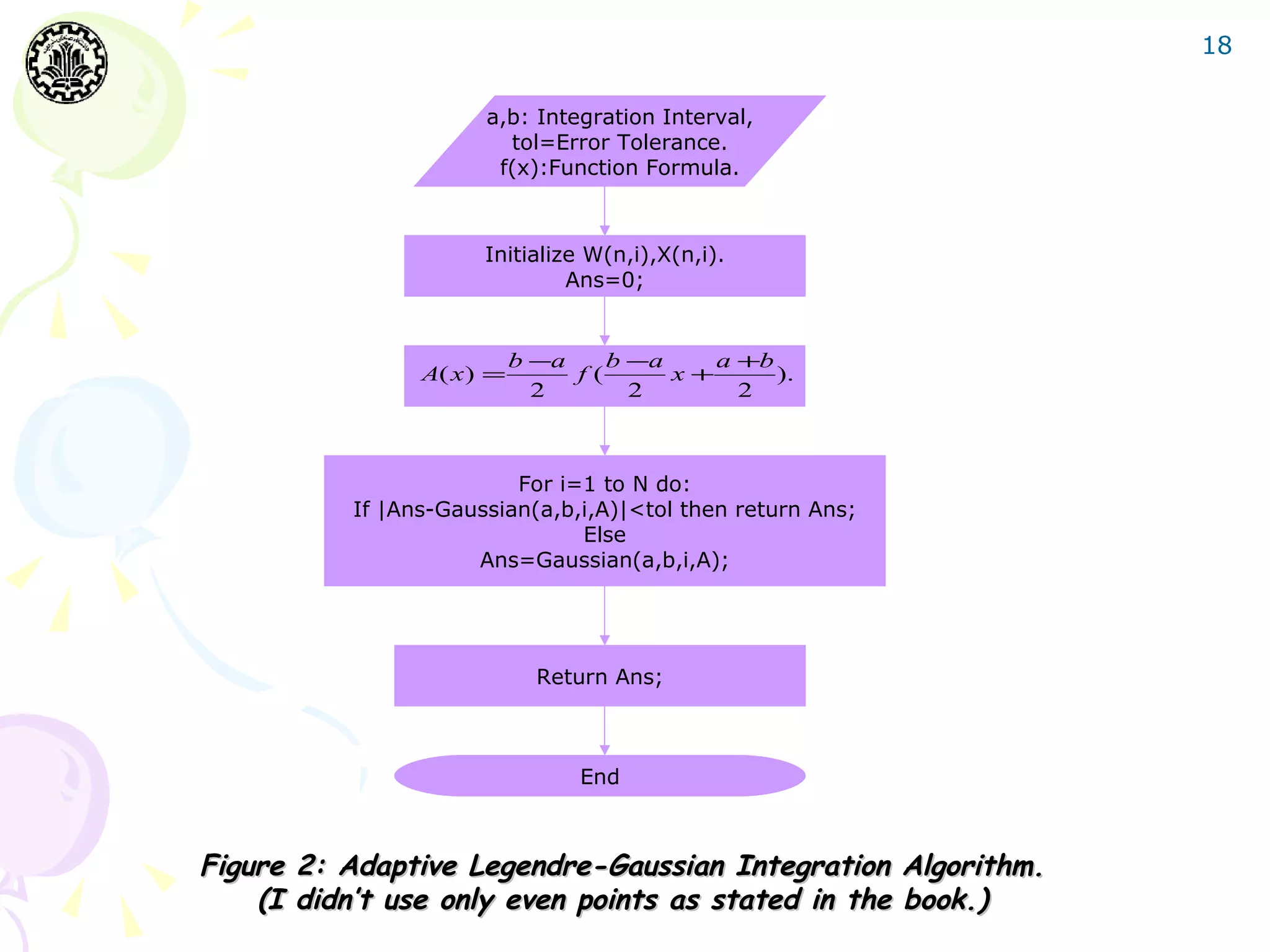
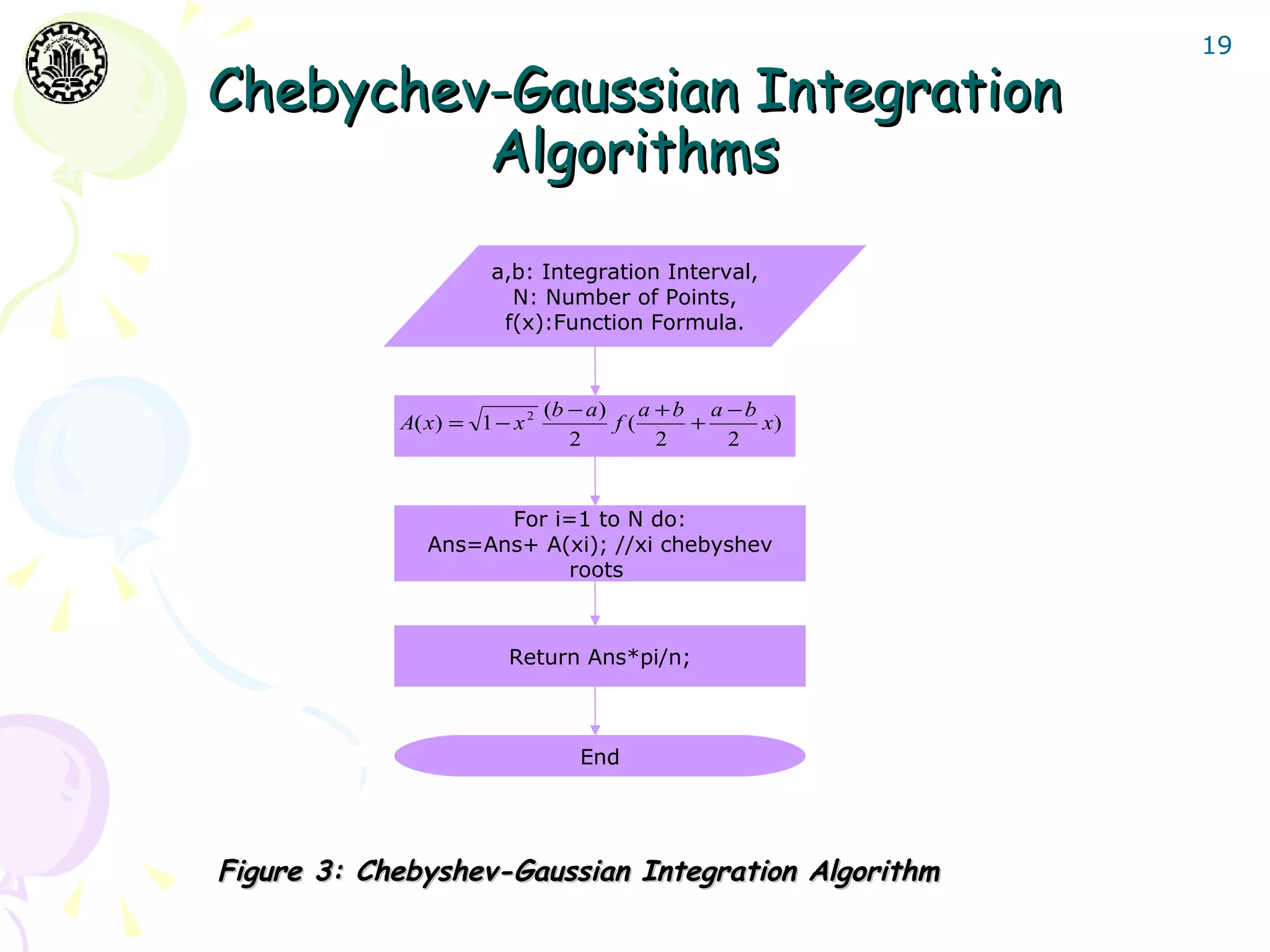
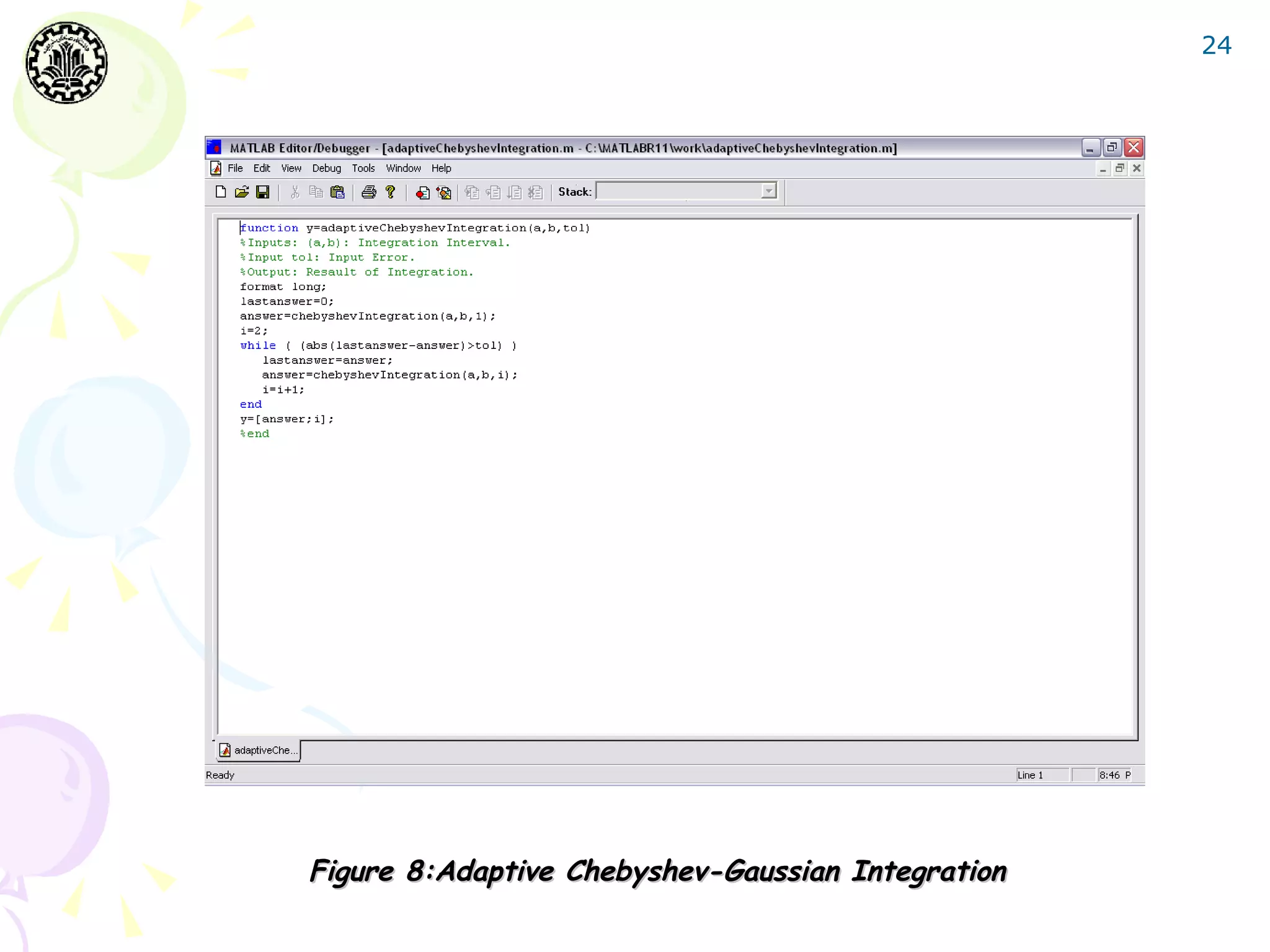
The document discusses Gaussian integration techniques, outlining their advantages over traditional methods like Newton-Cotes and Romberg integration, particularly highlighting the role of Legendre polynomials and Chebyshev polynomials in deriving Gaussian formulas for accurate numerical integration. It covers error analysis, implications for improper integrals, and provides MATLAB implementation examples with results demonstrating the effectiveness of these algorithms. Additionally, various algorithms for Legendre and Chebyshev integration are presented, alongside error tolerance considerations and sample computational results.

1. 1
Gaussian
Integration
M. Reza Rahimi,
Sharif University of Technology,
Tehran, Iran.

2. 2
Outline
• Introduction
• Gaussian Integration
• Legendre Polynomials
• N-Point Gaussian Formula
• Error Analysis for Gaussian Integration
• Gaussian Integration for Improper Integrals
• Legendre-Gaussian Integration Algorithms
• Chebyshev-Gaussian Integration Algorithms
• Examples, MATLAB Implementation and Results
• Conclusion

3. 3
Introduction
• Newton-Cotes and Romberg Integration usually use
table of the values of function.
• These methods are exact for polynomials less than N
degrees.
• General formula of these methods are as bellow:
b n
∫ f ( x)dx ≅ ∑w
a i =1
i f ( xi )
• In Newton-Cotes method the subintervals has the
same length.

4. 4
• But in Gaussian Integration we have the exact
formula of function.
• The points and weights are distinct for specific
number N.

5. 5
Gaussian Integration
• For Newton-Cotes methods we have:
b
b −a
1. ∫ f ( x )dx ≅ [ f (a) + f (b)].
a
2
b
b −a  a +b 
2. ∫
b
f ( x )dx ≅
6 
f (a ) + 4 f (
2
) + f (b) .

• And in general form:
b n
∫ f ( x)dx ≅ ∑ w f ( x )i i xi = a + (i − 1)h i ∈ {1,2,3,..., n}
a i =1
n
b− a n t− j
wi = ∏ dt
n − 1 ∫ j =1, j ≠ i i − j
0

6. 6
• But suppose that the distance among points are not
equal, and for every w and x we want the integration
to be exact for polynomial of degree less than 2n-1.
n 1
1.∑ wi = ∫ dx
i =1 −1
n 1
2.∑ xi wi = ∫ xdx
i =1 −1
.............
n 1
2n.∑ x 2 n −1 wi = ∫ x 2 n −1 dx
i =1 −1

7. 7
• Lets look at an example:
n =2 w1 , w2 , x1 , x 2 .
 .w1 + w2 = 2
1
2.x w + x w = 0
 1 1

2 2
1
2 ⇒2,4 ∴x 1 = x 2 ⇒3 ∴x 1 = .
2 2 2
 2
 .x 1 w1 + x 2 w2 = 3
2
3 3
 3
4.x 1 w1 + x 3 2 w2 = 0

1
x1 = −x 2 = , w1 = w2 =1.
3
• So 2-point Gaussian formula is:
1
1 −1
−
∫
1
f ( x ) dx ≅ f (
3
)+ f(
3
).

8. 8
Legendre Polynomials
• Fortunately each x is the roots of Legendre Polynomial.
1 d 2
PN ( x) = ( x − 1) n . n = 0,1,2,.....
2 n n! dx
• We have the following properties for Legendre
Polynomials.
1.Pn ( x) Has N Zeros in interval(-1,1).
2.( n +1) Pn +1 ( x ) = ( 2n +1) xPn ( x ) − nPn −1 ( x).
1
2
3. ∫ Pn ( x ) Pm ( x) dx = δmn
−1
2mn +1
1
4. ∫ x k Pn ( x) dx = 0 k = 0,1,2......, n - 1
−1
2 n +1 ( n!) 2
1
5.∫ x Pn ( x ) dx =
n
-1
(2n +1)!

9. 9
• Legendre Polynomials make orthogonal bases in (-1,1)
interval.
• So for finding Ws we must solve the following
equations:
n 1
1.∑ wi = ∫ dx = 2
i =1 −1
n 1
2.∑ wi x 2
i = ∫ xdx = 0
i =1 −1
....................
....................
n 1
1
n.∑ wi x n −1i = ∫ x n −1 dx = (1 − (−1) n )
i =1 −1
n

10. 10
• We have the following equation which has unique
answer:
... x1   w1   
n −1 T 2
1 x1  
   
1 x2 ... x 2   w2  
n −1 0 
   . = . 
 ... ... ... ...    
1 
1 ... x n   wn   n (1 − (− 1) ) 
n −1 n
 xn     
• Theorem: if Xs are the roots of legendre polynomials
1
and we got W from above equation then ∫P ( x)dx is −
1
exact for P ∈Π2 n −1 .

11. 11
• Proof:
p ∈ Π 2 n −1 ⇒ p( x) = q ( x) Pn ( x) + r ( x).
n −1 n −1
q( x) = ∑ q j Pj ( x) ; r ( x) = ∑ r j Pj ( x).
j =0 j =0
1 1 1 n −1 n −1
∫ p( x)dx = ∫ (q( x) P ( x) + r ( x))dx = ∫ ( P ( x)∑ q P ( x) + ∑ r P ( x))dx =
-1 −1
n
−1
n
j =0
j j
j =0
j j
n −1 1 n −1 1
∑ q ∫ P ( x) P ( x)dx + ∑ r ∫ P ( x) P (x)dx = 2r .
j =0
j j n
j =0
j 0 j 0
−1 −1
⇒
n n n
∑ w p( x ) = ∑ w (q( x ) P
i =1
i i
i =1
i i N ( x) + r ( xi )) = ∑ wi r ( xi )
i =1
n n −1 n −1 n n −1 1
= ∑ wi ∑ r j Pj ( xi ) = ∑ r j ∑ wi Pj ( x) = ∑ r j ∫ Pj ( x)dx = 2r0 .
i =1 j =0 j =0 i =1 j =0 −1

12. 12
Theorem:
1 n (x − x j )
wi = ∫ [ Li ( x )] dx ∏ (x
2
Li ( x ) =
−1 j = , j ≠i
1 i −xj )
Proof:
1 2
[ Li ( x)] 2 ∈ Π 2 n−2 ⇒ ∫ [ Li ( x)] 2 = ∑ w j [ Li ( x j )]
n
= wi .
−1 j =1

13. 13
Error Analysis for
Gaussian Integration
• Error analysis for Gaussian integrals can be derived
according to Hermite Interpolation.
b
Theorem : The error made by gaussian integration in approximation the integral ∫ f ( x )dx is ::
a
(b − a ) 2 n +1 ( N !) 4
EN ( f ) = f (2n)
(ξ ) ξ ∈ [ a, b].
(2n + 1)((2n)!) 3

14. 14
Gaussian Integration for Improper
Integrals
• Suppose we want to compute the following integral:
1
f ( x)
∫
−1 1−x2
dx
• Using Newton-Cotes methods are not useful in here
because they need the end points results.
• We must use the following:
1 1−ε
f ( x) f ( x)
∫
−1 1− x 2
dx ≅ ∫ε
−1+ 1− x 2
dx

15. 15
• But we can use the Gaussian formula because it does
not need the value at the endpoints.
• But according to the error of Gaussian integration,
Gaussian integration is also not proper in this case.
• We need better approach.
Definition : The Polynomial set { Pi } is orthogonal in (a, b) with respect to w(x) if :
b
∫ w( x) P ( x)P
a
i j ( x) dx = 0 for i ≠ j
then we have the following approximation :
b n
∫ w( x) f ( x)dx ≅ ∑ wi f ( xi )
a i =1
where xi are the roots for Pn and
b
wi = ∫ w( x)[ Li ( x)] dx
2
a
will compute the integral exactly when f ∈ Π 2 n −1

16. 16
Definition : Chebyshev Polynomials Tn ( x ) is defined as :
n 
2 
 
n 
Tn ( x ) = ∑ x n −2 k ( x 2 −1) k
 
k =0  2 k 
Tn ( x ) = 2 xTn ( x) − Tn −1 ( x), n ≥ 1, T0 ( x) = 1, T1 ( x ) = x.
If - 1 ≤ x ≤ 1 then :
( 2i −1)π 
Tn ( x ) = cos( n arccos x). roots xi = cos  .
 2n 
1
1
∫
−1 1−x 2
Ti ( x )T j ( x ) dx = 0 if i ≠ j.
• So we have following approximation:
1
1 π n  (2i − 1)π 
∫ f ( x)dx ≅ ∑ f ( xi ), xi = cos 
n i =1  2n   i ∈ {1,2,3,..., n}.
−1 1− x2

17. Legendre-Gaussian Integration
17
Algorithms
a,b: Integration Interval,
N: Number of Points,
f(x):Function Formula.
Initialize W(n,i),X(n,i).
Ans=0;
b−a b−a a+b
A( x ) = f( x+ ).
2 2 2
For i=1 to N do:
Ans=Ans+W(N,i)*A(X(N,i));
Return Ans;
End
Figure 1: Legendre-Gaussian Integration Algorithm

18. 18
a,b: Integration Interval,
tol=Error Tolerance.
f(x):Function Formula.
Initialize W(n,i),X(n,i).
Ans=0;
b −a b −a a +b
A( x ) = f( x+ ).
2 2 2
For i=1 to N do:
If |Ans-Gaussian(a,b,i,A)|<tol then return Ans;
Else
Ans=Gaussian(a,b,i,A);
Return Ans;
End
Figure 2: Adaptive Legendre-Gaussian Integration Algorithm.
(I didn’t use only even points as stated in the book.)

19. 19
Chebychev-Gaussian Integration
Algorithms
a,b: Integration Interval,
N: Number of Points,
f(x):Function Formula.
(b − a ) a +b a −b
A( x) = 1 − x 2 f( + x)
2 2 2
For i=1 to N do:
Ans=Ans+ A(xi); //xi chebyshev
roots
Return Ans*pi/n;
End
Figure 3: Chebyshev-Gaussian Integration Algorithm

20. 20
a,b: Integration Interval,
tol=Error Tolerance.
f(x):Function Formula.
(b − a ) a + b a − b
A( x ) = 1 − x 2 f( + x)
2 2 2
For i=1 to N do:
If |Ans-Chebyshev(a,b,I,A)|<tol then return Ans;
Else
Ans=Chebyshev(a,b,I,A);
Return Ans;
End
Figure 4: Adaptive Chebyshev-Gaussian Integration Algorithm

21. 21
Example and MATLAB
Implementation and Results
Figure 5:Legendre-Gaussian Integration

22. 22
Figure 6: Adaptive Legendre-Gaussian Integration

23. 23
Figure 7:Chebyshev-Gaussian Integration

24. 24
Figure 8:Adaptive Chebyshev-Gaussian Integration

25. 25
Testing Strategies:
• The software has been tested for
polynomials less or equal than 2N-1
degrees.
• It has been tested for some random inputs.
• Its Result has been compared with MATLAB
Trapz function.

26. 26
Examples:
Example 1:Gaussian-Legendre
1
1 π
∫ 2
−1 1 + x
dx exact → Arc tan(1) − Arc tan(−1) = ≅ 1.5707.

2
1 − (−1) 1 1
Trapezoid →(
  )( + ) = 1.0000.
2 1 + (−1) 2
1 + (1) 2
1 − (−1) 1 1 1
Simpson →(
 )( +4 + ) ≅ 1.6667.
6 1 + (−1) 2 1 + (0) 2 1 + (1) 2
2− Po int Gaussian → According To Software Resualt = 1.5000.
 
3−Po int Gaussian → According To Software Resualt = 1.5833.
 

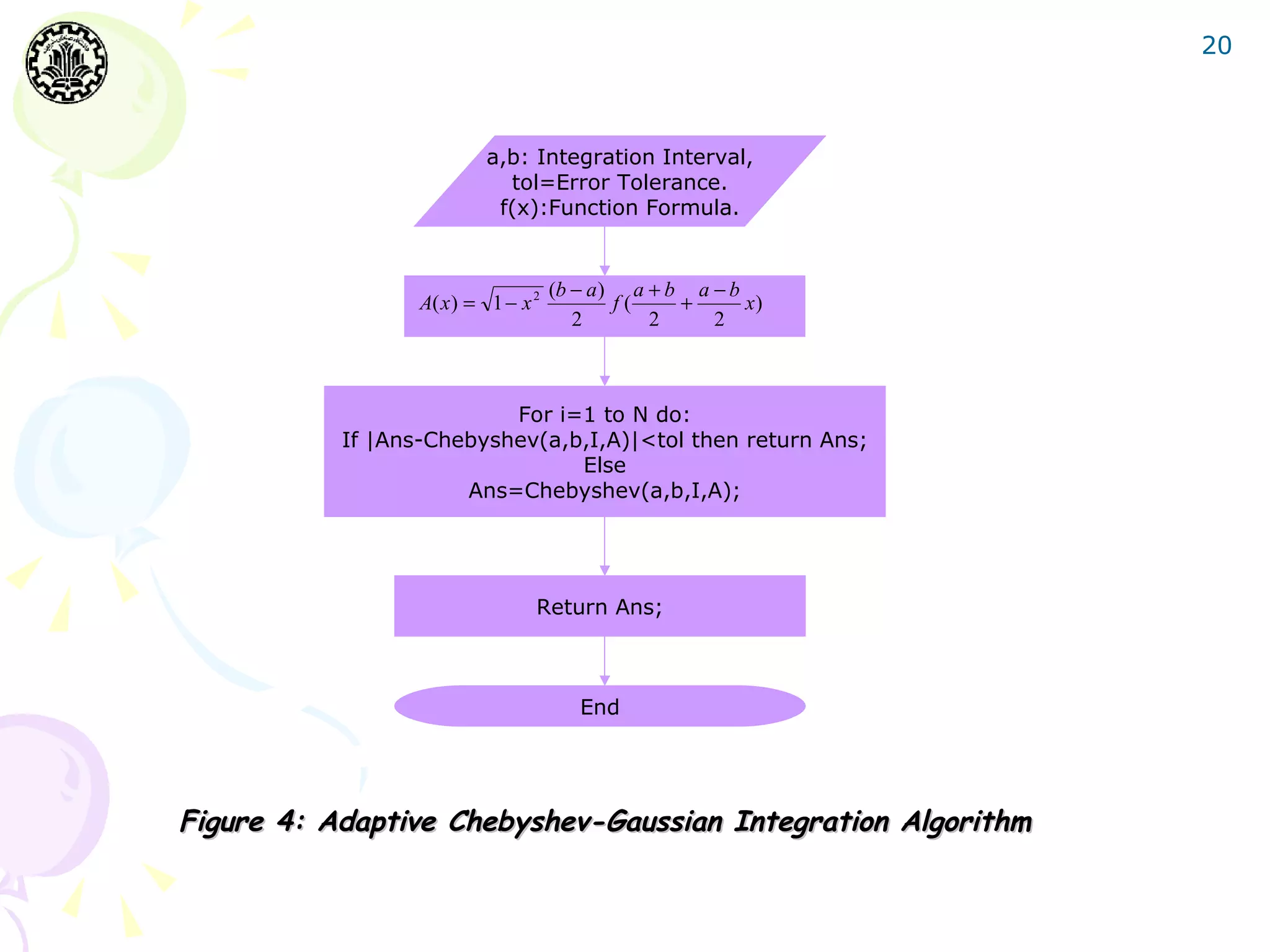
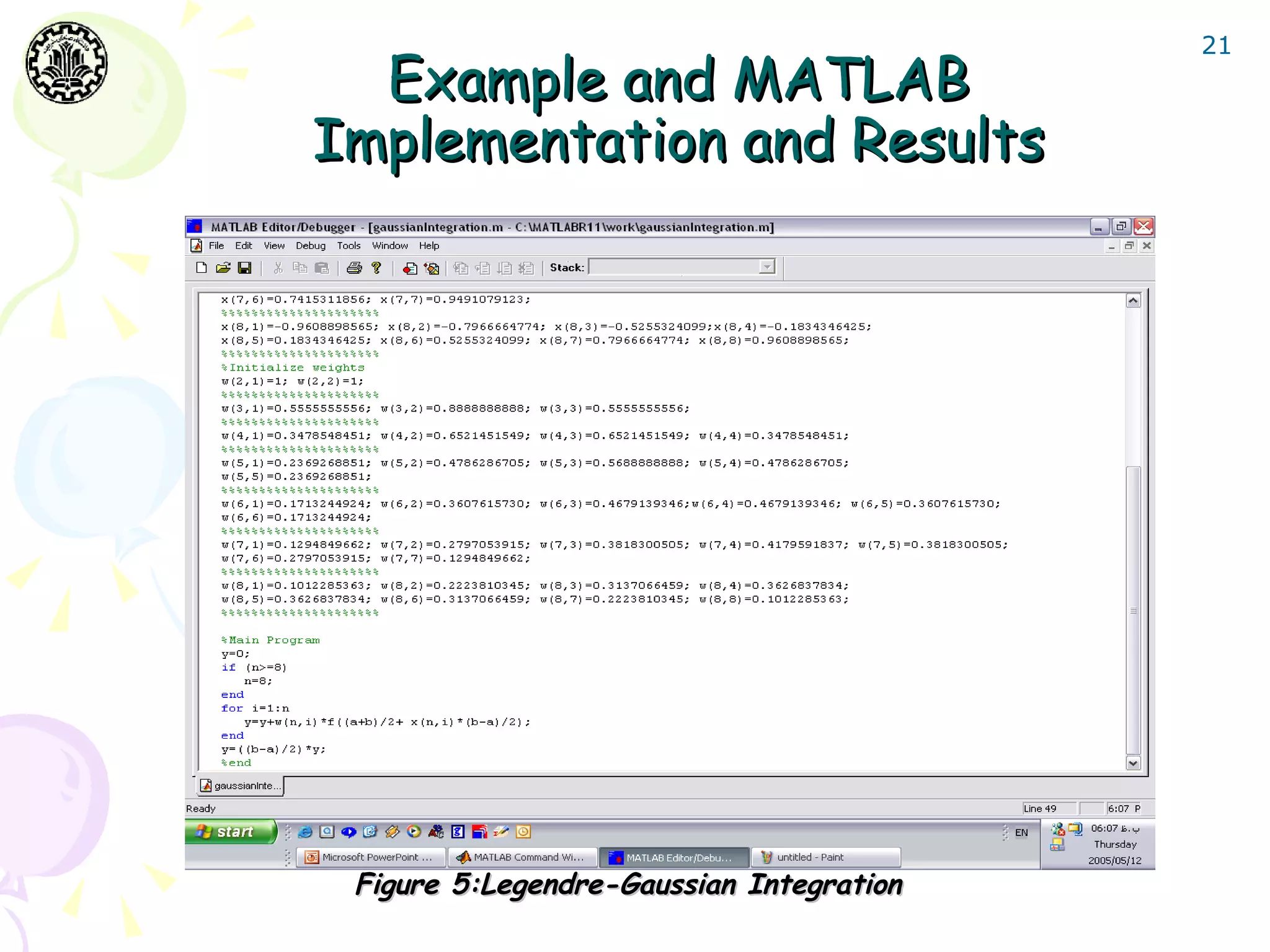
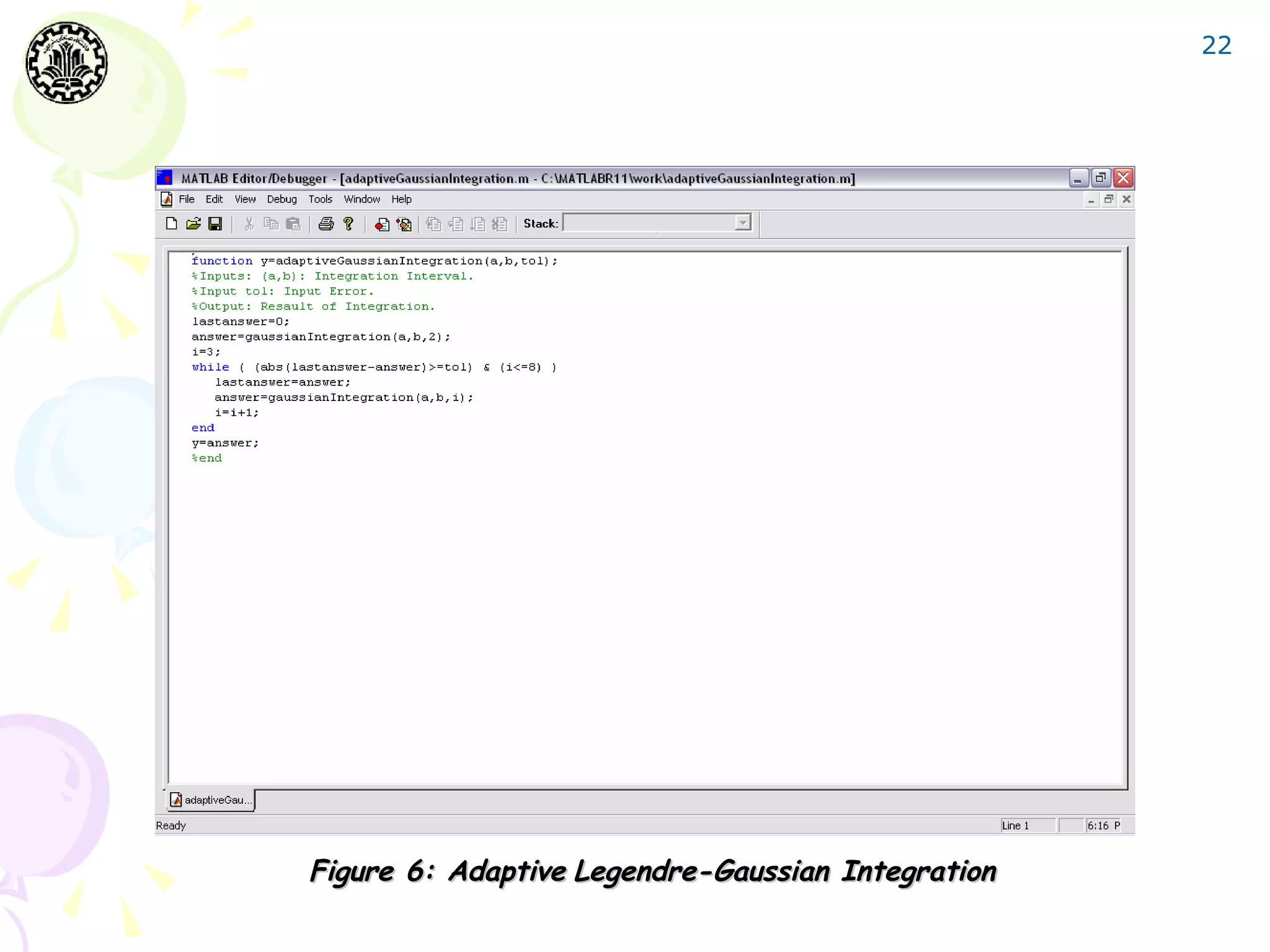
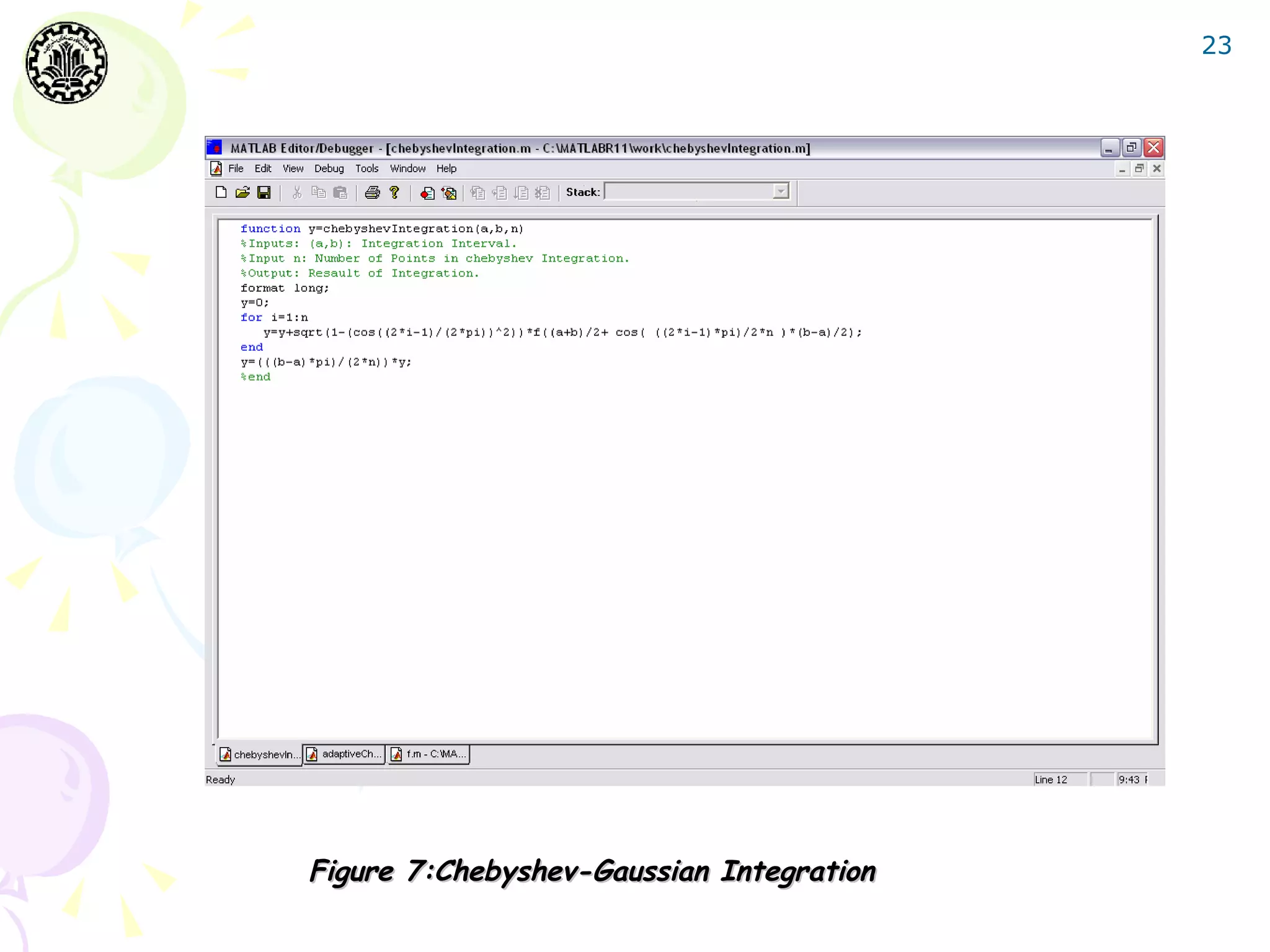
27. 27
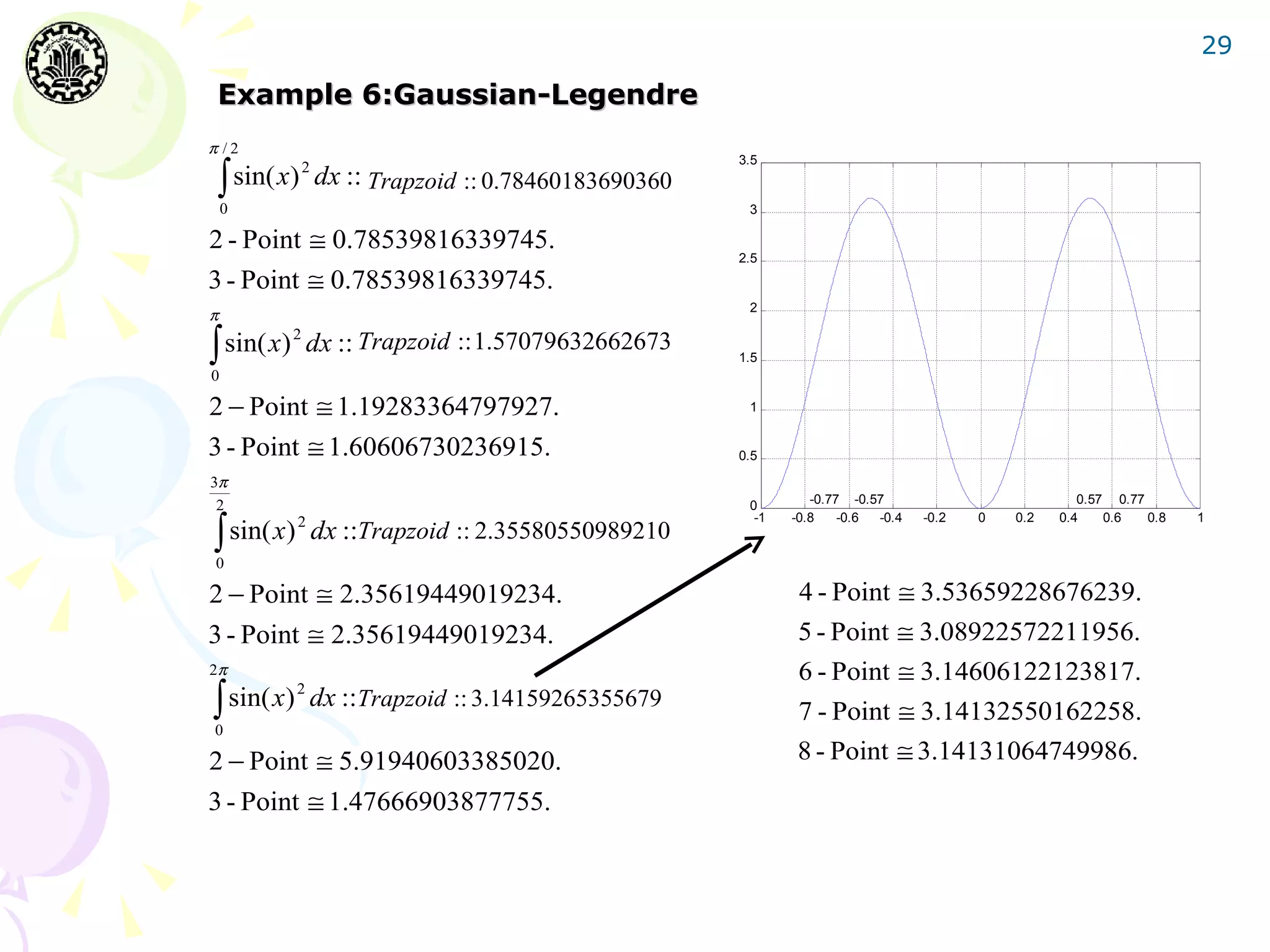
Example 2:Gaussian-Legendre
2
− e−x 3 − e −9 1
3
∫ xe
2
−x
dx  →(

exact
)0 = ( + ) ≅ 0.4999.
0
2 2 2
3− 0
Trapezoid →(
  )(0 + 3e −9 ) ≅ 0.0005.
2
3−0 2
Simpson → (
 )(0 + 1.5e −1.5 + 3e −9 ) ≅ 0.0792.
6
2− Po int Gaussian → ≅ 0.6494.
 
3− Po int Gaussian → ≅ 0.4640.
 
Example 3:Gaussian-Legendre
(b − a ) 2 n +1 ( n!) 4
En ( f ) = f 2n
(ξ ) ξ ∈[a, b].
( 2n +1)((2n)!) 3
π
(π − 0) 2 n +1 ( n!) 4
∫ sin( x)dx  → | (2n +1)((2n)!) 3 sin (ξ ) |≤ 5 ×10 ⇒ n ≥ 4.
−4
 2n
0
( 2 − 0) 2 n +1 (n!) 4 −ξ
2
∫ e dx  →| (2n +1)((2n)!) 3 e |≤ 5 ×10 ⇒ n ≥ 3.
−x −4

0

28. 28
Example 4:Gaussian-Legendre
3
x 1
∫0 1 + x 2 dx = ln(1 + x 2 ) ≅ 1.15129.
2
2 ⇒ ≅ 1.21622 ⇒ errora ≅ 0.06493.
3 ⇒≅ 1.14258 ⇒ errora ≅ 0.00871.
4 ⇒≅ 1.14902 ⇒ errora ≅ 0.36227.
5 ⇒≅ 1.15156 ⇒ errora ≅ 0.00027.
6 ⇒≅ 1.15137 ⇒ errora ≅ 0.00008.
Example 5:Gaussian-Legendre
3 2 3
e−x
∫ xe
2
−x
dx = ≅ 0.49994.
0
−2 0
2 ⇒≅ 0.64937 ⇒ errora ≅ 0.14943.
3 ⇒≅ 0.46397 ⇒ errora ≅ 0.03597.
4 ⇒≅ 0.50269 ⇒ errora ≅ 0.00275.
5 ⇒≅ 0.50007 ⇒ errora ≅ 0.00013.
6 ⇒≅ 0.49989 ⇒ errora ≅ 0.00005.

29. 29
Example 6:Gaussian-Legendre
π /2
∫ sin( x) dx :: Trapzoid :: 0.78460183690360
3.5
2
0 3
2 - Point ≅ 0.78539816339745.
2.5
3 - Point ≅ 0.78539816339745.
2
π
∫ sin( x)
2
dx :: Trapzoid :: 1.57079632662673 1.5
0
2 − Point ≅ 1.19283364797927. 1
3 - Point ≅ 1.60606730236915. 0.5
3π
2 0 -0.77 -0.57 0.57 0.77
∫ sin( x)
2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
dx ::Trapzoid :: 2.35580550989210
0
2 − Point ≅ 2.35619449019234. 4 - Point ≅ 3.53659228676239.
3 - Point ≅ 2.35619449019234. 5 - Point ≅ 3.08922572211956.
2π 6 - Point ≅ 3.14606122123817.
∫ sin( x)
2
dx ::Trapzoid :: 3.14159265355679
7 - Point ≅ 3.14132550162258.
0
2 − Point ≅ 5.91940603385020. 8 - Point ≅ 3.14131064749986.
3 - Point ≅ 1.47666903877755.

30. 30
Example 7:Adaptive Gaussian-Legendre
3
x
∫ 1 + x 2 dx ::
0
1)Adaptive Gaussian Integration :: error ≈ 5 ×10 -5 ⇒ 1.15114335351486.
2)Adaptive Gaussian Integration :: error ≈ 5 ×10 -4 ⇒ 1.15137188448013.
3
∫
2
xe x dx ::
0
1)Adaptive Gaussian Integration :: error ≈ 5 × 10 -5 ⇒ 0.49980229291620.
2)Adaptive Gaussian Integration :: error ≈ 5 × 10 -4 ⇒ 0.49988858784837.

31. 31
Example 8:Gaussian-Chebyshev
2 - Point Chebyshev Integration ≈ 0.48538619428604.
3 - Point Chebyshev Integration ≈ 1.39530571408271
2 - Point Chebyshev :: 0
3 - Point Chebyshev :: 0.33089431565488.

32. 32
Example 9:
1) w1 + w2 + w3 = 2
2) w1 x1 + w2 x 2 + w3 x3 = 0
2 2 2 2
3) w1 x1 + w2 x 2 + w3 x3 =
3
3 3 3
4) w1 x1 + w2 x 2 + w3 x3 =0
4 4 4 2
5) w1 x1 + w2 x 2 + w3 x3 =
5
5 5 5
6) w1 x1 + w2 x 2 + w3 x3 =0
w1 x1 + w2 x 2 1 
2,4 ⇒ 3 3
= 2 
w1 x1 + w2 x 2 x3  2 2 2 2 3 2 2 3 2 2
3 3  ⇒ w1 x1 ( x1 − x3 ) = w2 x 2 ( x3 − x 2 ), w1 x1 ( x3 − x1 ) = w2 x 2 ( x 2 − x3 )
w1 x1 + w2 x 2 1
4,5 ⇒ = 2
x3 
5 5
w1 x1 + w2 x 2 
⇒ x1 = − x 2
2 2 2 2
⇒ w1 x1 ( x1 − x3 ) = w2 (− x1 )( x3 − x1 ) ⇒ w1 = w2
w1 = w2 , x1 = − x 2 ⇒ 2) ⇒ w3 x3 = 0.
 
2 2 4 2
3,5 ⇒ 2w1 x1 = ,2 w1 x1 = . ⇒  x1 =
3
= − x2  ( w1 , w2 , w3 ) =  5 , 5 , 8 
 
3 5  5  9 9 9
2 5 8  3 3 
2
⇒ 2w1 x1 = ⇒ w1 = w2 = ⇒ 1 ⇒ w3 = ⇒ x3 = 0 ( x1 , x 2 , x3 ) = 
 ,− , 0 
3 9 9  5 5  

33. 33
Conclusion
• In this talk I focused on Gaussian Integration.
• It is shown that this method has good error
bound and very useful when we have exact
formula.
• Using Adaptive methods is Recommended Highly.
• General technique for this kind of integration
also presented.
• The MATLAB codes has been also explained.