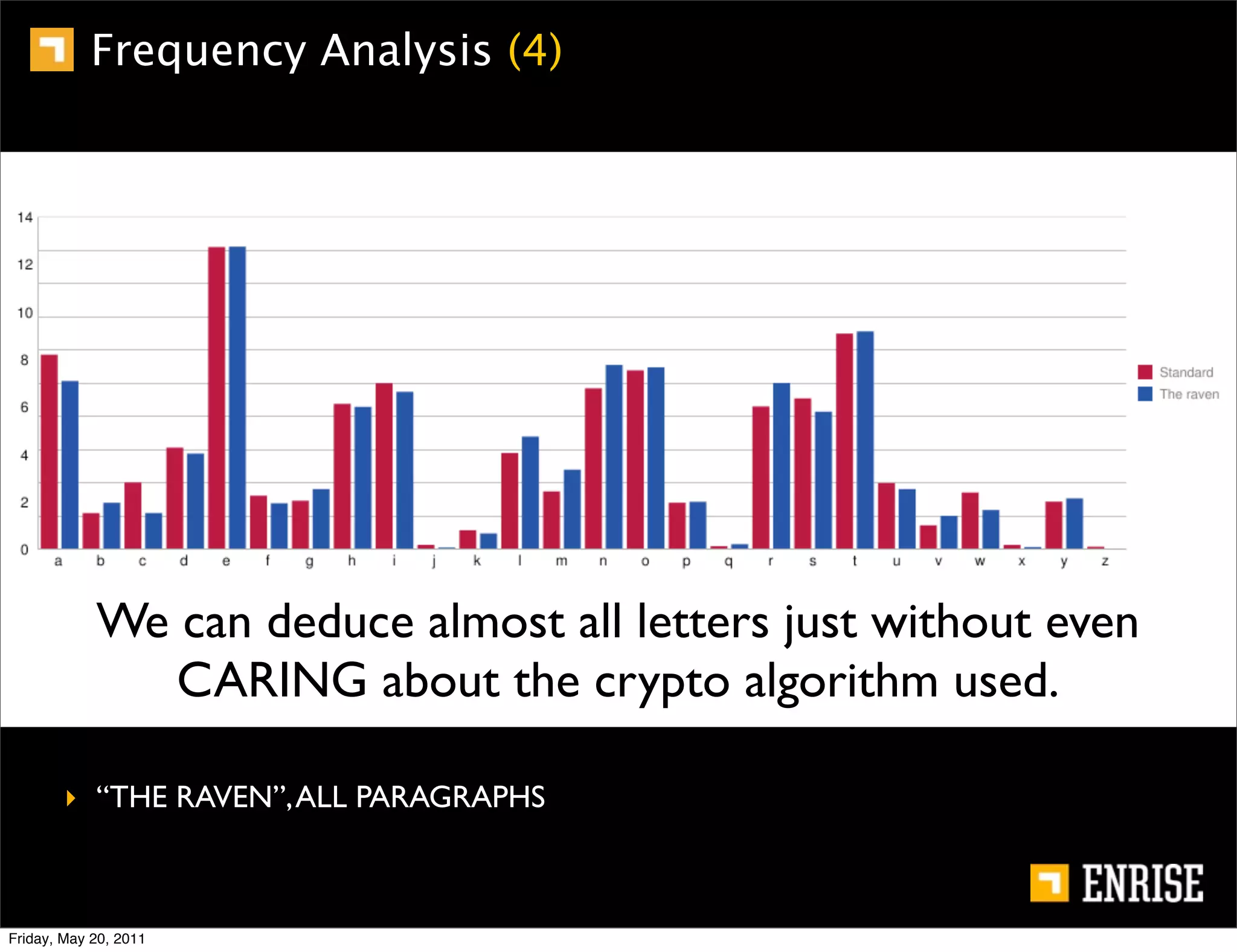
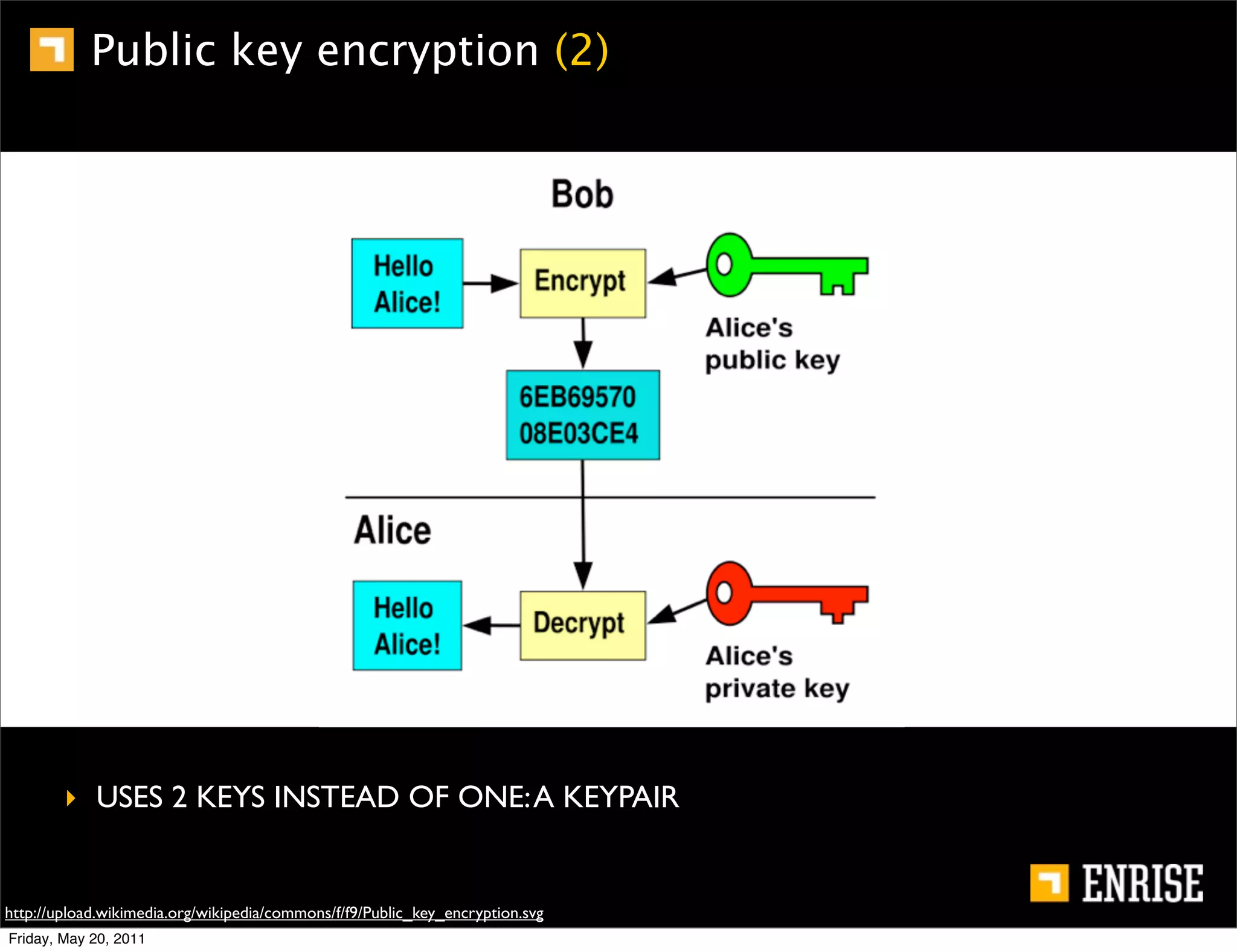
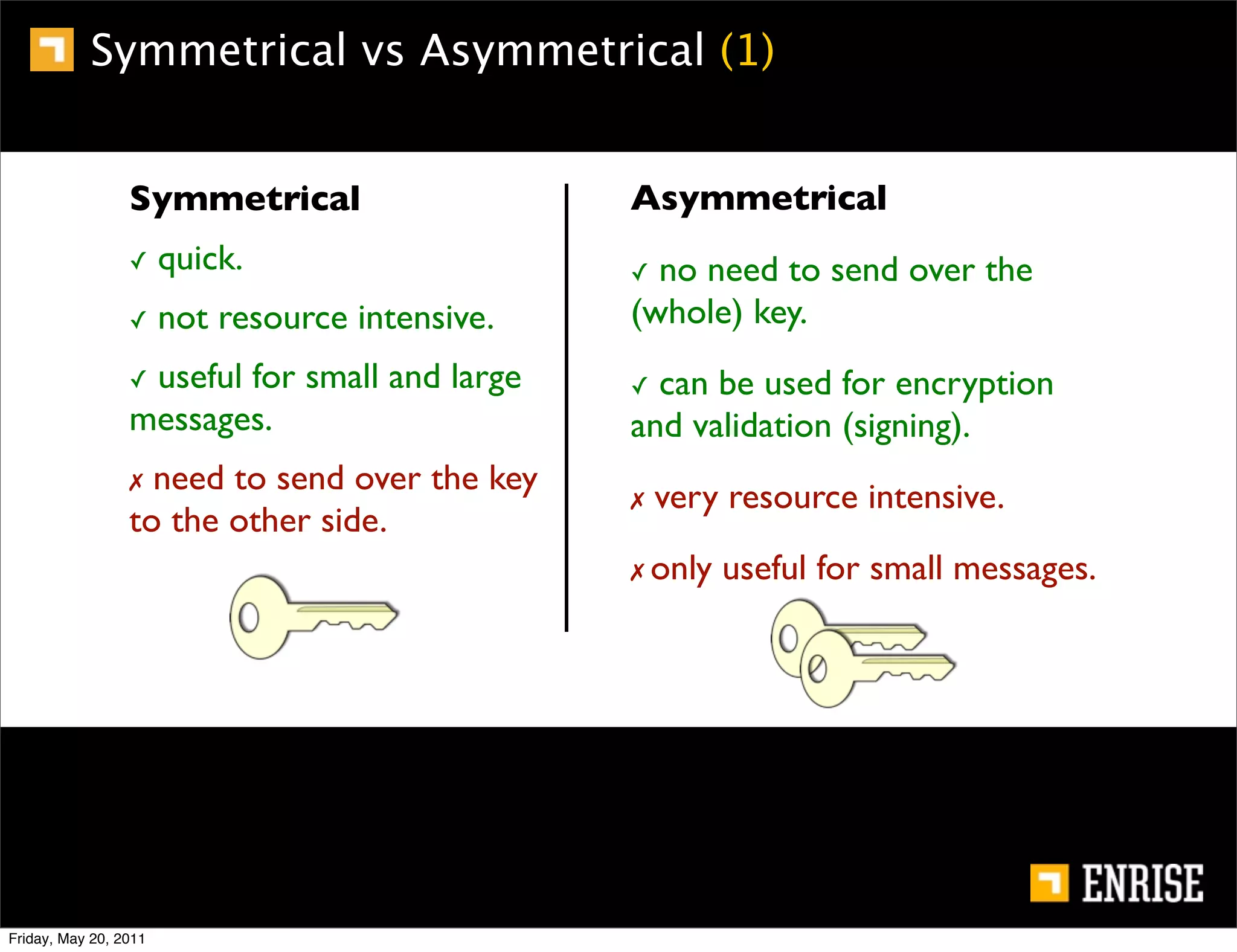
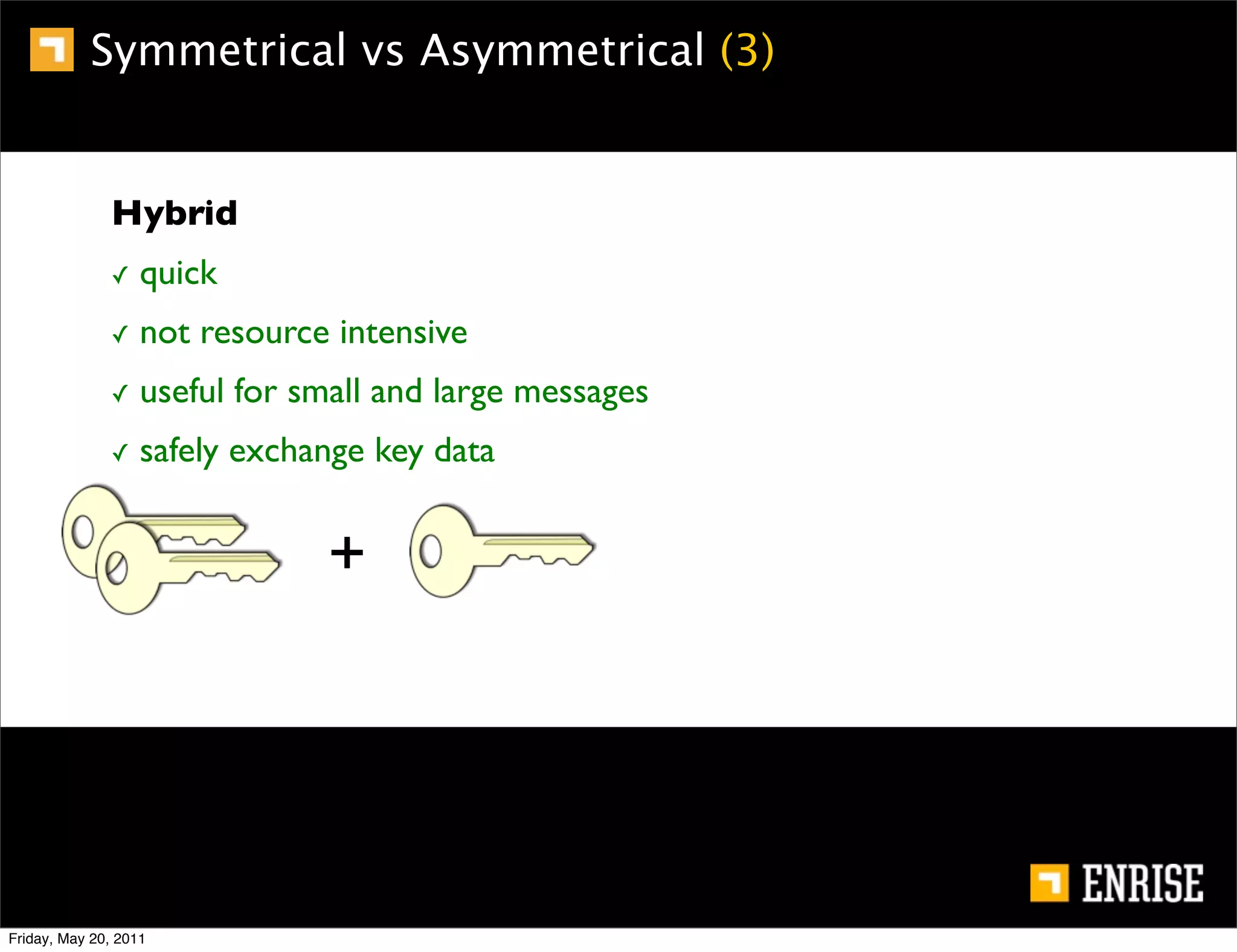
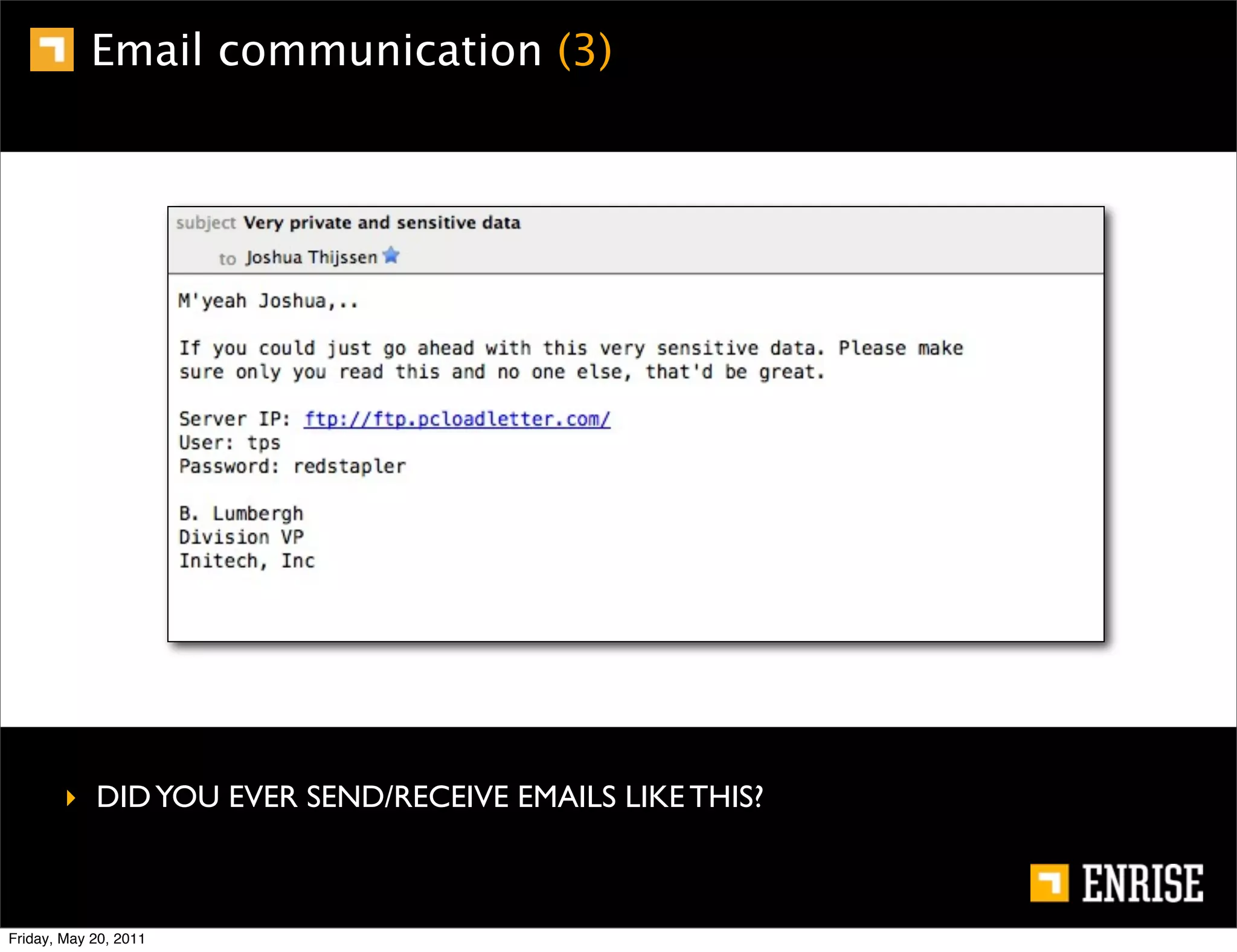
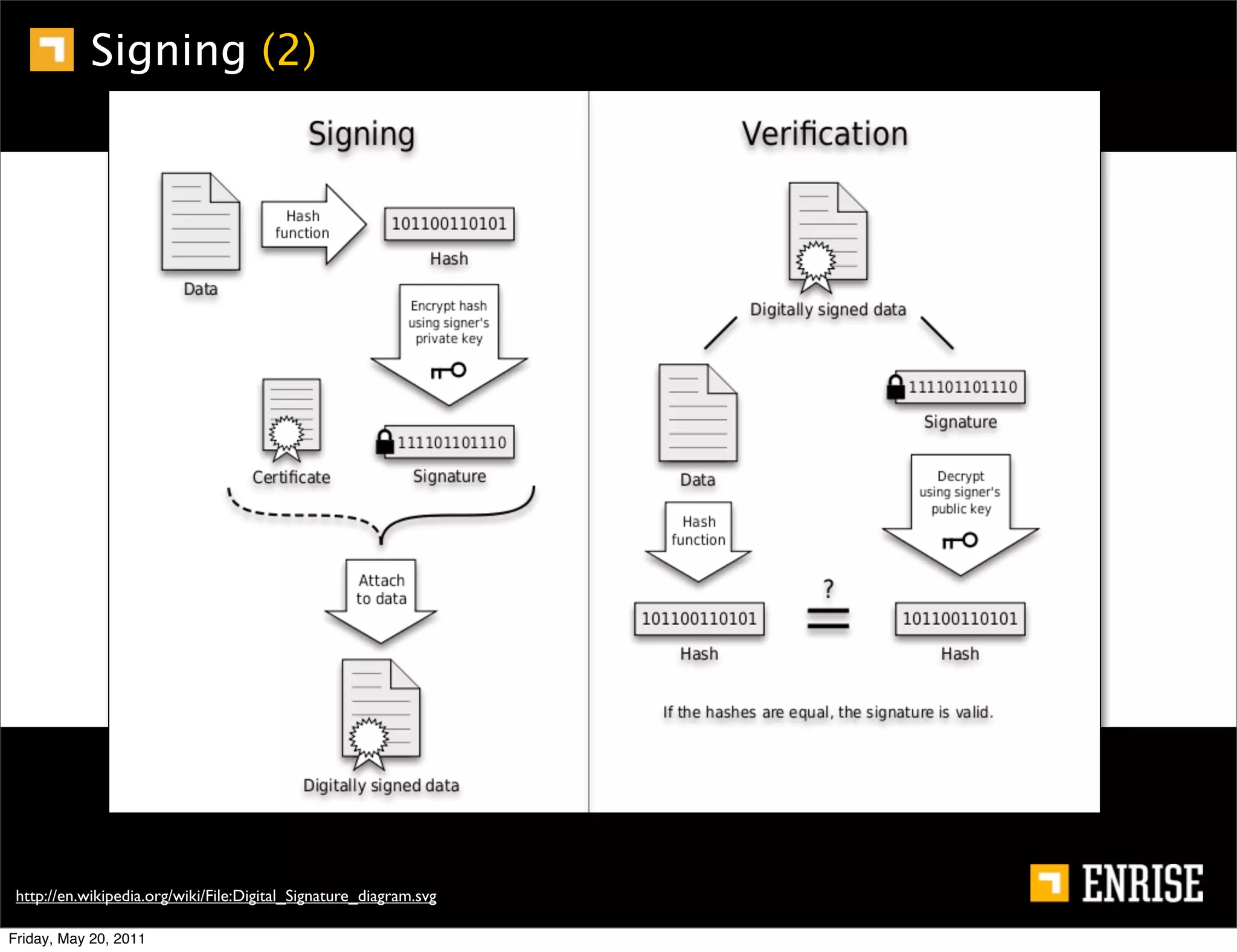
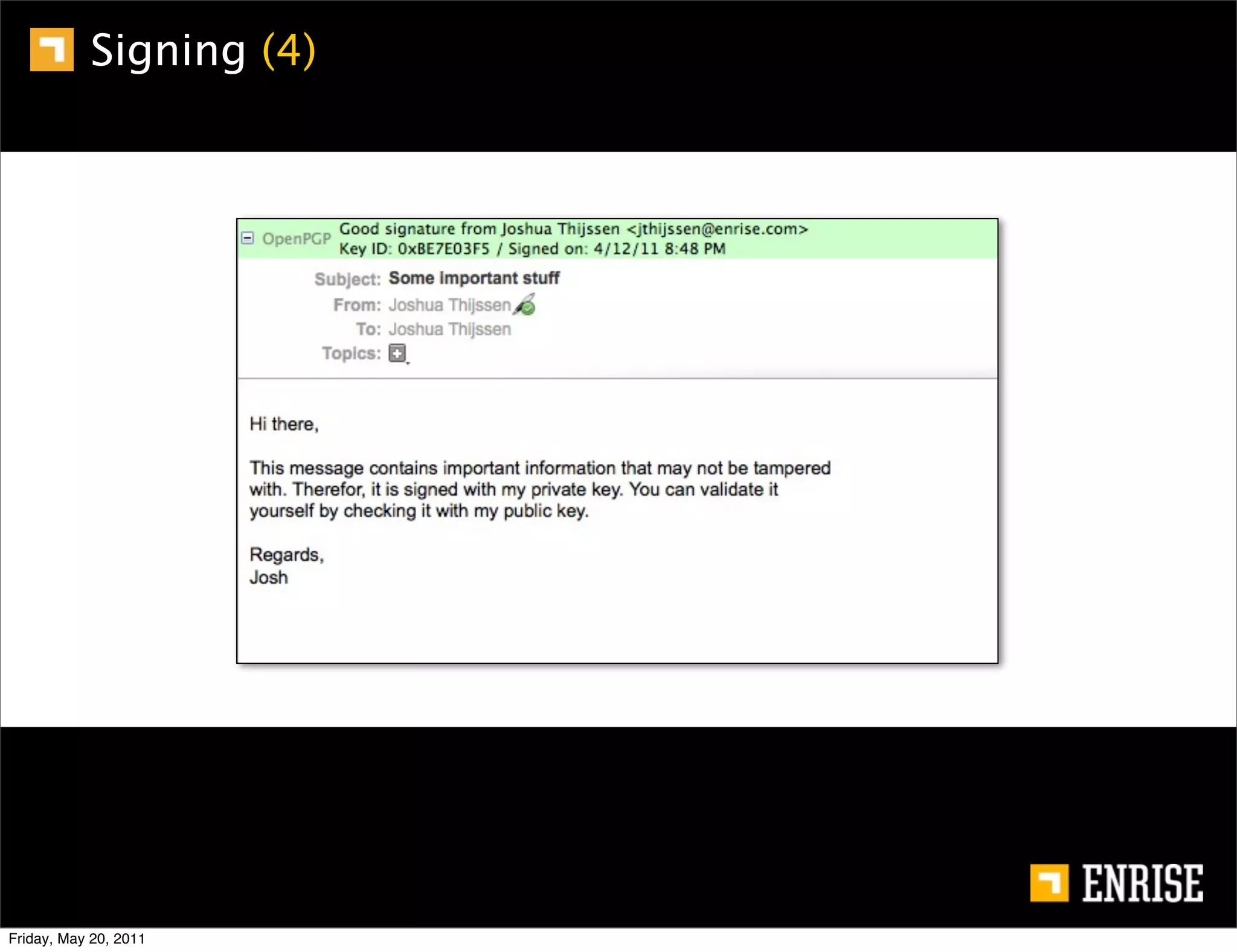
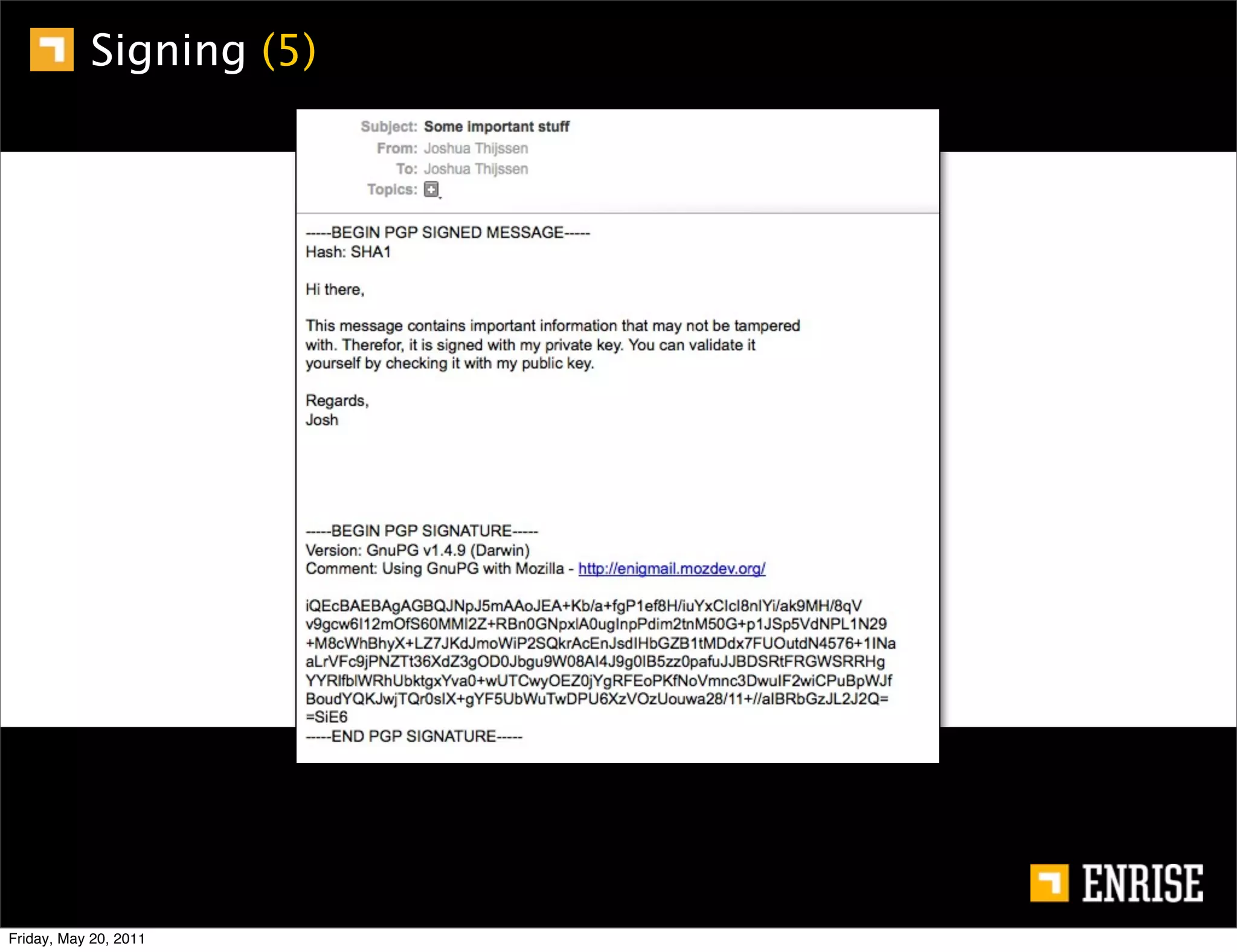
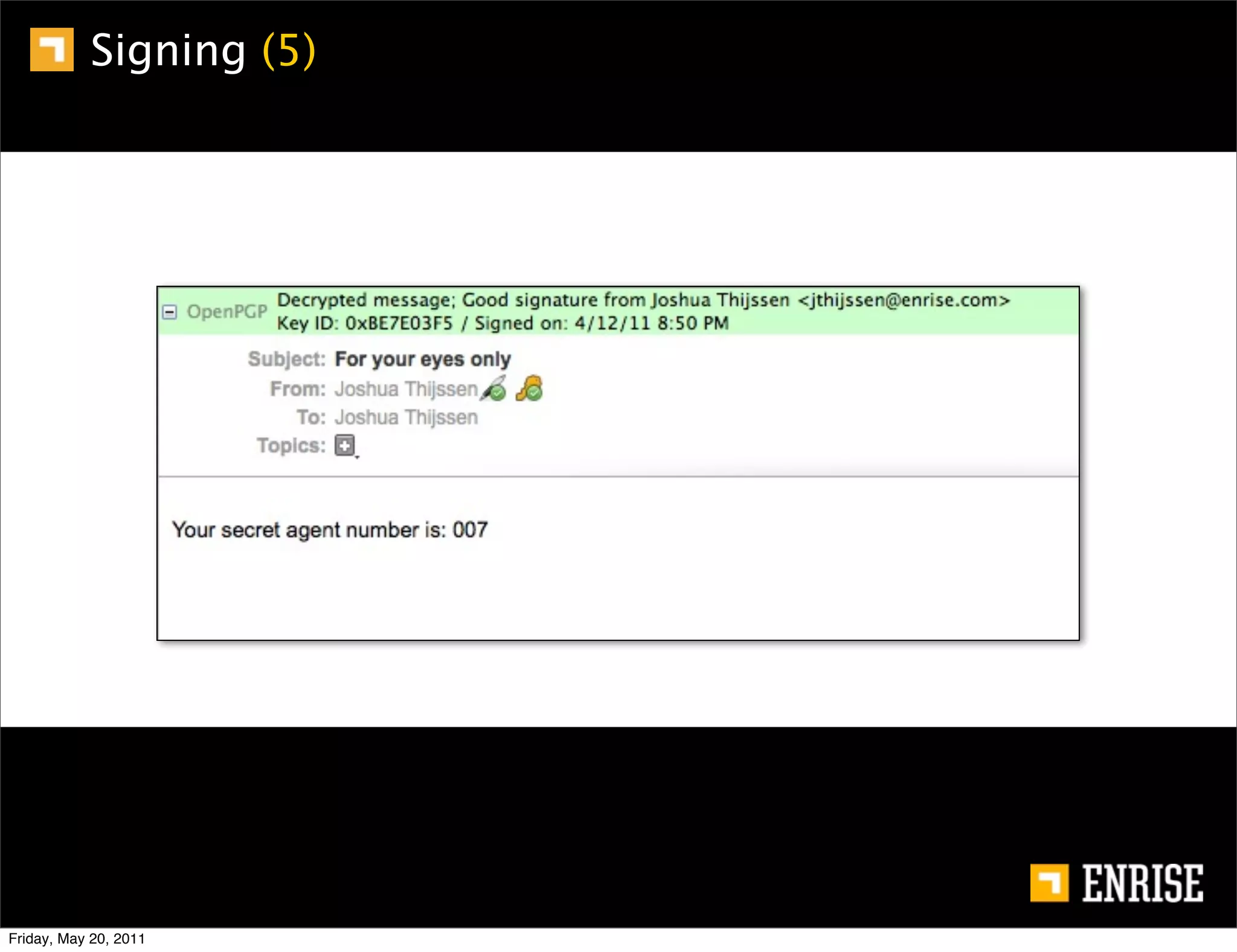
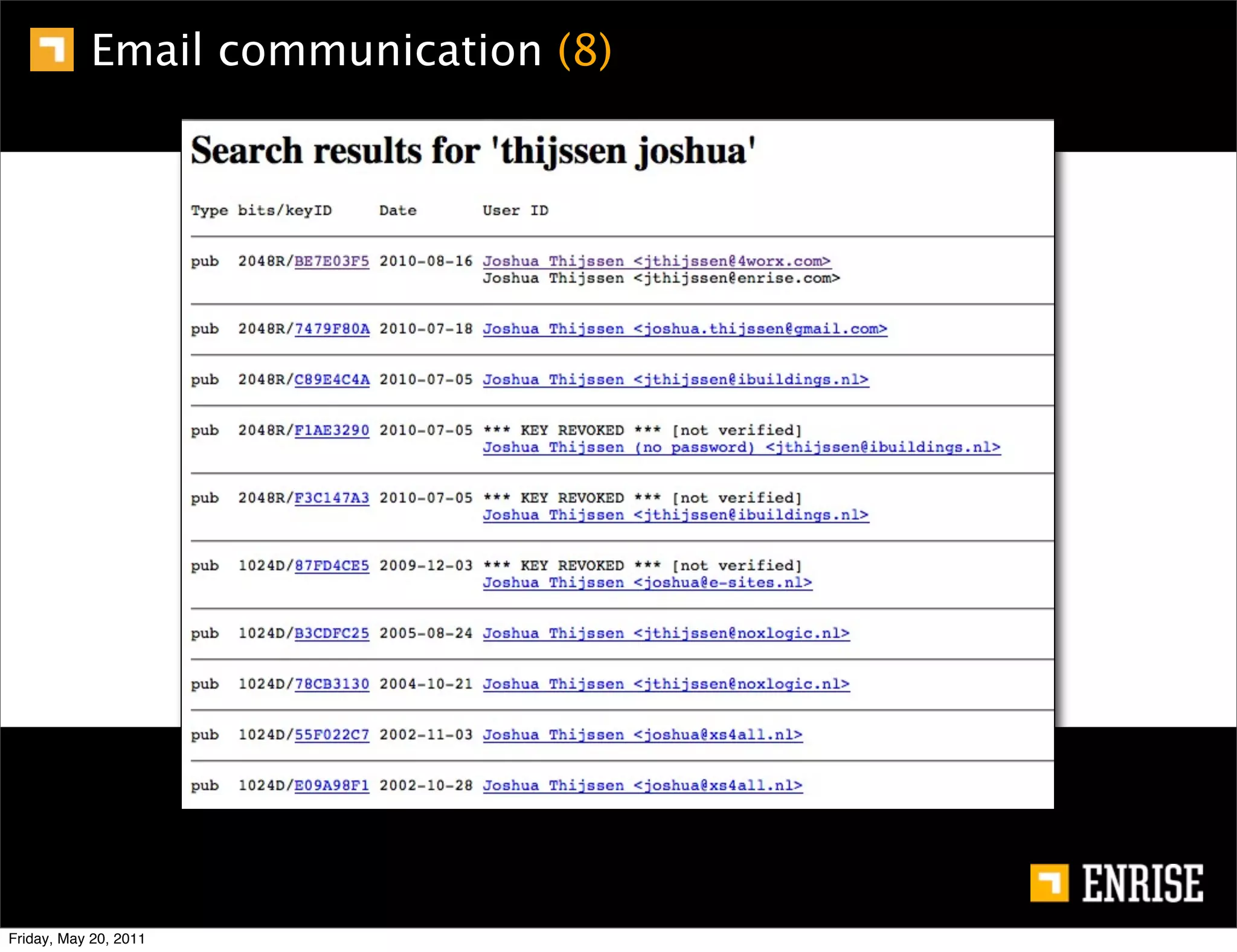
This document provides an introduction to public key cryptography. It begins with an overview of Alice and Bob, who represent the two parties in a communication. It then discusses the history of encryption, including weaknesses in early ciphers like substitution and Caesar ciphers. Frequency analysis is introduced as a way to break these simple ciphers. Symmetric encryption algorithms are discussed along with the key distribution problem they present. The document then introduces public key encryption as an solution, using two keys: a public key that can encrypt and a private key for decrypting. RSA is presented as the most widely used public key algorithm, and its workings are outlined at a high level.