This document provides information about reading and writing numbers in English. It discusses cardinal and ordinal numbers, writing multi-digit numbers, decimals, fractions, and percentages. It also covers operations like addition and subtraction. Cardinal numbers refer to quantity while ordinal numbers refer to distribution or order. Multi-digit numbers are written as words or hyphenated depending on the digits. Decimals are said figure by figure while fractions use "and" or ordinal numbers. Percentages omit the article before the numeral. Addition combines numbers to get a total while subtraction removes numbers.

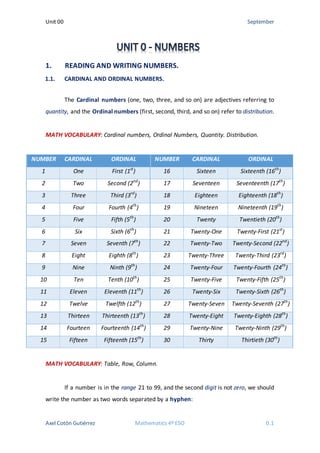
1. Unit 00 September
1. READING AND WRITING NUMBERS.
1.1. CARDINAL AND ORDINAL NUMBERS.
The Cardinal numbers (one, two, three, and so on) are adjectives referring to
quantity, and the Ordinal numbers (first, second, third, and so on) refer to distribution.
MATH VOCABULARY: Cardinal numbers, Ordinal Numbers, Quantity. Distribution.
NUMBER CARDINAL ORDINAL NUMBER CARDINAL ORDINAL
1 One First (1st
) 16 Sixteen Sixteenth (16th
)
2 Two Second (2nd
) 17 Seventeen Seventeenth (17th
)
3 Three Third (3rd
) 18 Eighteen Eighteenth (18th
)
4 Four Fourth (4th
) 19 Nineteen Nineteenth (19th
)
5 Five Fifth (5th
) 20 Twenty Twentieth (20th
)
6 Six Sixth (6th
) 21 Twenty-One Twenty-First (21st
)
7 Seven Seventh (7th
) 22 Twenty-Two Twenty-Second (22nd
)
8 Eight Eighth (8th
) 23 Twenty-Three Twenty-Third (23rd
)
9 Nine Ninth (9th
) 24 Twenty-Four Twenty-Fourth (24th
)
10 Ten Tenth (10th
) 25 Twenty-Five Twenty-Fifth (25th
)
11 Eleven Eleventh (11th
) 26 Twenty-Six Twenty-Sixth (26th
)
12 Twelve Twelfth (12th
) 27 Twenty-Seven Twenty-Seventh (27th
)
13 Thirteen Thirteenth (13th
) 28 Twenty-Eight Twenty-Eighth (28th
)
14 Fourteen Fourteenth (14th
) 29 Twenty-Nine Twenty-Ninth (29th
)
15 Fifteen Fifteenth (15th
) 30 Thirty Thirtieth (30th
)
MATH VOCABULARY: Table, Row, Column.
If a number is in the range 21 to 99, and the second digit is not zero, we should
write the number as two words separated by a hyphen:
Axel Cotón Gutiérrez Mathematics 4º ESO 0.1

2. Unit 00 September
25 twenty-five
57 fifty-seven
89 eighty-nine
MATH VOCABULARY: Range, Digit, Zero, Hyphen.
NUMBER CARDINAL ORDINAL NUMBER CARDINAL ORDINAL
40 Forty Fortieth (40th
) 80 Eighty Eightieth (80th
)
50 Fifty Fiftieth (50th
) 90 Ninety Ninetieth (90th
)
60 Sixty Sixtieth (60th
) 100 A/One Hundred Hundredth (100th
)
70 Seventy Seventieth (70th
) 1,000 A/One Thousand Thousandth (1,000th
)
Numbers over 100 are generally written in figures. If you want to say them
aloud or want to write them in words rather than figures you put ‘and’ in front of the
number expressed by the last two figures. For example:
203 two hundred and three (AmE: two hundred three)
622 six hundred and twenty-two (AmE: six hundred twenty-two)
MATH VOCABULARY: Figure.
NOTE: The British use ‘and’ before tens and ones but the Americans usually leave the
‘and’ out.
NUMBER CARDINAL ORDINAL
10,000 Ten Thousand Ten Thousandth
100,000 A/One Hundred Thousand Hundred Thousandth
1,000,000 A/One Million Millionth
Numbers between 1000 and 1,000,000 are usually said or written in words as:
Axel Cotón Gutiérrez Mathematics 4º ESO 0.2

3. Unit 00 September
1,803 one thousand, eight hundred and three
1,963 one thousand, nine hundred and sixty-three
2,840 two thousand, eight hundred and forty
NOTE: Notice that hundred, thousand, and so on is NOT followed by an ‘s’: two
hundred (NOT two hundreds ).
Four-figure numbers ending in 00 can also be said or written as a number of
hundreds. For example:
1800 can be said or written as ‘eighteen hundred’
If the number 1963 is being used to identify something, it is said as ‘one nine six
three’. We always say each figure separately like this with telephone numbers. If a
telephone number contains a double number, we used the word ‘double’:
561 6603 five six one (pause) double six ‘oh’ three
(AmE: five six one (pause) six six ‘oh’ three)
MATH VOCABULARY: Double, Ones, Tens.
Beyond a million, the names of the numbers differ depending where you live.
The places are grouped by thousands in America and France, by the millions in Great
Britain, Germany and Spain.
NAME AMERICA UK
Billion 1,000,000,000 1,000,000,000,000
Trillion 1 with 12 zeros 1 with 18 zeros
Quadrillion 1 with 15 zeros 1 with 24 zeros
1,412,605 one million four hundred twelve thousand six hundred and five
2,760,300 two million seven hundred sixty thousand three hundred
Axel Cotón Gutiérrez Mathematics 4º ESO 0.3

4. Unit 00 September
1.2. SAYING YEARS AND DATES.
YEARS
We normally say a year in two parts. In the case of years ending in ‘00’, we say
the second part in ‘hundred’:
1058 ten fifty-eight
1706 seventeen hundred and six (or ‘seventeen oh six’)
1865 eighteen sixty-five
1900 nineteen hundred
There are two ways of saying years ending in ‘01’ to ‘09’ before 2000. For
example:
1901 can be said as ‘nineteen oh one’ or ‘nineteen hundred and one’
The year 2000 is read ‘two thousand’, 2006 ‘two thousand and six’ (AmE: two
thousand six).
Post-2010 dates are often said as normal (2010 would be ‘twenty ten’).
DATES
We can say dates either with the day before the month, or the month before
the day.
The first of January / January the first
NOTE: Be careful! The second of December 2007 is written in British English like this:
2/12/07 and in American English like this: 12/2/07
Axel Cotón Gutiérrez Mathematics 4º ESO 0.4

5. Unit 00 September
1.3. FLIGHT NUMBERS AND TITLES.
FLIGHT NUMBERS
We pronounce a flight number in two parts or digit-by-digit. For example:
110 one ten (or ‘one one oh’)
1248 twelve forty-eight
2503 twenty-five oh three
3050 three oh five oh (or ‘three zero five zero’, ‘thirty fifty)
TITLES
In names for kings and queens, ordinal numbers are written in Roman numbers.
In spoken English, the definite article is used before the ordinal number:
Charles II - Charles the Second
Edward VI - Eduard the Sixth
Henry VIII - Henry the Eighth
1.4. NUMBER 0.
The figure 0 is normally called nought in UK and zero in USA. When numbers
are said figure by figure, 0 is often called like the letter O Examples:
My telephone number is nine six seven double two oh four six oh (967 220460)
My telephone number is nine six seven double two oh treble/triple six (967 220666)
In measurements (for instance, of temperature), 0 is called zero
Water freezes at zero degrees Celsius
Axel Cotón Gutiérrez Mathematics 4º ESO 0.5

6. Unit 00 September
Zero scores in team-games are usually called nil in UK and zero in USA. In
tennis, table-tennis and similar games the word love is used (this is derived from the
French l’oeuf, meaning the egg, presumably because zero can be egg-shaped)
Examples:
Ribera del Fresno three Real Madrid nil (nothing)
Nadal is winning forty-love
MATH VOCABULARY: Measurement, Love, Nought, Nil.
1.5. DECIMALS, FRACTIONS AND PERCENTAGES.
DECIMALS
Decimal Fractions are said with each figure separate. We use a full stop (called
“point”), not a comma, before the fraction. Each place value has a value that is one
tenth the value to the immediate left of it.
3.375 three point three seven five
2.36 two point three six
0.5 nought point five (AmE: zero point five)
0.75 nought point seven five (AmE: zero point seven five)
Axel Cotón Gutiérrez Mathematics 4º ESO 0.6

7. Unit 00 September
MATH VOCABULARY: Decimal, Fraction, Value.
FRACTIONS
Simple fractions are expressed by using “ordinal numbers” (third, fourth,
fifth...) with some exceptions:
1/2 One half / a half
1/3 One third / a third
2/3 Two thirds
3/4 Three quarters
5/8 Five eighths
4/33 Four over thirty-three
MATH VOCABULARY: Over. Quarter, Half.
PERCENTAGES.
We don't use the article in front of the numeral.
10% of the people – Ten per cent of the people
37% thirty-seven per cent
MATH VOCABULARY: Percentage, Per Cent, Numeral.
REMEMBER: Use (,) and (.) in the opposite way –the points for the decimals and the
commas for thousands, millions, and so on.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.7

8. Unit 00 September
2. NATURAL NUMBERS.
The numbers we use for counting are called natural numbers or sometimes just
counting numbers. The possible combination of natural numbers is endless. There is
no largest natural number, so we say the set of all natural numbers is infinite. We use
the letter ℕ to refer to the set of all natural numbers.
ℕ = {1, 2, 3, 4, . . . , 10, 11, . . . }
If we include the number zero or 0, then our set now has a new name, which is
the set of whole numbers.
{0, 1, 2, 3, 4, . . . , 10, 11, . . . }
The Hindu-Arabic system is more useful and more efficient than the systems
used by the Egyptians, Romans, and Mayans.
• It uses only 10 digits to construct all the natural numbers.
• It uses the digit 0 or zero to show an empty place value.
• It has a place value system where digits represent different numbers when
placed in different place value columns.
Each digit in a number has a place value.
This system is called also Decimal system (its base is 10).
Axel Cotón Gutiérrez Mathematics 4º ESO 0.8

9. Unit 00 September
MATH VOCABULARY: Natural Numbers, Whole Numbers, Infinite, Counting Numbers,
Decimal System, Twice, Average.
3. REPRESENTATION AND ORDER NATURAL NUMBERS.
The Natural numbers can be represented by a line like that:
We can use symbols < and > to express which is the order relation between
two numbers: less than and more than.
Example: “Order the following pairs of numbers: 3 and 9; 4 and 5; 9 and 8”.
We can write:
3 < 9 “3 is smaller than 9”
4 < 5 “4 is smaller than 5”
9 > 8 “9 is greater than 8”
If you have any doubts then check the correspondent position in the number line:
To compare and order whole numbers:
• Align the digits by place value.
• Compare the digits in each place, starting with the greatest place.
39,630 19,578 130,434 36,415
There are no hundred thousands in the other numbers. 130,434 is greatest.
39,630 36,415
3 = 3, but the ones of thousands period 9 is bigger than 6, so 39,630 is greatest.
In order from greatest to least, the numbers are:
130,434 > 39,639 > 36,415 > 19,578
Axel Cotón Gutiérrez Mathematics 4º ESO 0.9

10. Unit 00 September
4. OPERATIONS WITH NATURAL NUMBERS.
Many situations in real life involve operations with numbers so it is useful to
practice them. We strongly recommend you practice them mentally.
4.1. ADDITION.
The addition is an operation that combines numbers to get a total. The symbol
is +.
Example: 3 + 5 = 8
We read 3 + 5 = 8 as: “Three plus five is equal to eight” or “Three plus five
equals eight” or “Three plus five is eight”. The terms in the addition are called addends
and the result is called the sum.
Example: The library lent 45 books last Monday, 50 books on Tuesday and 73
books on Wednesday. How many books have they lent?
45 + 50 + 73 = 168 𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏
Answer: They have lent 168 books
We can use the Addition table:
Axel Cotón Gutiérrez Mathematics 4º ESO 0.10

11. Unit 00 September
ADDITION PROPERTIES.
The properties of addition are: closure, commutative, associative, and additive
identity.
• Closure property: Addition of two natural numbers is always another natural
number.
6 + 7 = 13 (13 is another natural number)
• Commutative property: When we add two natural numbers, the sum is the same
no matter what the order of the addends is.
𝒂𝒂 + 𝒃𝒃 = 𝒃𝒃 + 𝒂𝒂
4 + 2 = 2 + 4
• Associative Property: When we add three or more natural numbers, the sum is
the same no matter how we group the addends.
𝒂𝒂 + 𝒃𝒃 + 𝒄𝒄 = (𝒂𝒂 + 𝒃𝒃) + 𝒄𝒄 = 𝒂𝒂 + (𝒃𝒃 + 𝒄𝒄)
(2 + 3) + 4 = 2 + (3 + 4)
• Additive Identity Property: The sum of any natural number and zero is the
original number.
𝒂𝒂 + 𝟎𝟎 = 𝒂𝒂
5 + 0 = 5
MATH VOCABULARY: Operation, Addition, Plus, Equal, Term, Addends, Sum,
Properties, Closure Property, Commutative Property, Associative Property, Additive
Identity Property, To Group.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.11

12. Unit 00 September
4.2. SUBTRACTION.
Subtracting is removing or taking away some objects from a group. The symbol
is −.
Example: 13 – 7 = 6
We read 13 – 7 = 6 as: “Thirteen minus seven equals six” or “Thirteen subtract
seven equals six” (sometimes you can see “thirteen take away seven equals six” but it
is better to use the other expressions). The terms of subtraction are called minuend
(M) and subtrahend (S), the result is called the difference (D).
𝑴𝑴 − 𝑺𝑺 = 𝑫𝑫
The minuend is the first number, it is the number from which you take
something and it must be the larger number. The subtrahend is the number that is
subtracted and it must be the smaller number. The difference is the result of the
subtraction.
To check if the subtraction is correct we add up the subtrahend and the
difference. The result must be the minuend:
𝑺𝑺 + 𝑫𝑫 = 𝑴𝑴
Example: We have saved 3,520 euros but we have spent € 745 on a computer.
How much money do we have left?
3,520 – 745 = 2,775
Answer: We have 2,775 euros left.
SUBTRACTION PROPERTIES.
• The Subtraction is NOT Commutative.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.12

13. Unit 00 September
𝒂𝒂 − 𝒃𝒃 ≠ 𝒃𝒃 − 𝒂𝒂
3 − 2 ≠ 2 − 3
• The Subtraction in Natural Numbers has NOT Closure Property when 𝑺𝑺 > 𝑴𝑴.
2 − 3 = −1 (−1 is not a Natural Number)
• Associative Property: Only when 𝒂𝒂 > 𝒃𝒃 > 𝒄𝒄 𝒂𝒂𝒏𝒏𝒅𝒅 ( 𝒂𝒂 − 𝒃𝒃) > 𝒄𝒄.
𝒂𝒂 − 𝒃𝒃 − 𝒄𝒄 = ( 𝒂𝒂 − 𝒃𝒃) − 𝒄𝒄 = 𝒂𝒂 − (𝒃𝒃 − 𝒄𝒄)
(5 − 4) − 2 = 5 − (4 − 3)
5 > 4 > 3
• Additive Identity Property: To subtract zero to any natural number is the original
number.
𝒂𝒂 − 𝟎𝟎 = 𝒂𝒂
5 − 0 = 5
MATH VOCABULARY: Subtraction, To Remove, To Take Away, Minus, To Subtract,
Minuend, Subtrahend, Difference, Result, To Be Correct, To Spend.
4.3. MULTIPLICATION.
Multiplying is doing an addition of equal addends. . The symbol is 𝑥𝑥 or ∙.
3 + 3 + 3 + 3 + 3 = 3 𝑥𝑥 5 = 15
We read 3 𝑥𝑥 5 = 15 as: “Three times five equals fifteen” or “Three times five is
fifteen”. The factors are the numbers that are multiplied together. The product is the
result of multiplying.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.13

14. Unit 00 September
Example: In my living-room I have a bookcase with three shelves. If there are
five books on each shelf, how many books are there?
5 𝑥𝑥 3 = 15
Answer: There are 15 books in my bookcase.
We use the Multiplication Table:
To multiply a number by a unit followed by zeroes, you add the zeroes to the
right of the number.
28 ∙ 10 = 280
15 ∙ 1,000 = 15,000
PROPERTIES OF MULTIPLICATION.
The properties of multiplication are: closure, commutative, associative, and
additive identity:
Axel Cotón Gutiérrez Mathematics 4º ESO 0.14

15. Unit 00 September
• Closure property: Multiplication of two natural numbers is always another
natural number.
6 ∙ 7 = 42 (42 is another natural number)
• Commutative property: When two numbers are multiplied together, the product
is the same no matter what the order of the factors is.
𝒂𝒂 ∙ 𝒃𝒃 = 𝒃𝒃 ∙ 𝒂𝒂
4 ∙ 2 = 2 ∙ 4
• Associative Property: When three or more numbers are multiplied, the product is the
same no matter how we group the factors.
𝒂𝒂 ∙ 𝒃𝒃 ∙ 𝒄𝒄 = (𝒂𝒂 ∙ 𝒃𝒃) ∙ 𝒄𝒄 = 𝒂𝒂 ∙ (𝒃𝒃 ∙ 𝒄𝒄)
(2 ∙ 3) ∙ 4 = 2 ∙ (3 ∙ 4)
• Additive Identity Property: The product of any number and one is that number.
𝒂𝒂 ∙ 𝟏𝟏 = 𝒂𝒂
5 ∙ 1 = 5
• Zero Property of Multiplication: The product of zero and a number is zero.
𝒂𝒂 ∙ 𝟎𝟎 = 𝟎𝟎
5 ∙ 0 = 0
MATH VOCABULARY: To Multiply, Times, Factor, Product, Identity.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.15

16. Unit 00 September
4.4. DIVISION.
Dividing is to share a quantity into equal groups. It is the inverse of
multiplication. In Spanish we write 6 : 2 , but in English it is always 6 ÷ 2, we never use
the colon (:).
We read 15 ÷ 5 = 3 as: “Fifteen divided by five equals three”. There are four
terms in a division: dividend, divisor, quotient and remainder.
The dividend is the number that is divided. The divisor is the number that
divides the dividend. The quotient is the number of times the divisor goes into the
dividend. The remainder is a number that is too small to be divided by the divisor.
Example: There are 72 sweets in a bag. If we want to distribute them among 12
children, how many sweets are there for each child?
72 ∶ 12 = 6
Answer: There are six sweets for each child.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.16

17. Unit 00 September
The division can be:
• Exact: the remainder is 0.
• Non exact: the remainder isn’t 0.
To check if the division is correct we do the Division Algorithm:
𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫 = 𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫 ∙ 𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸𝑸 + 𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹𝑹
Example: Find out the result of the division 237 ÷ 13 and then check the result
with the division algorithm:
237 ÷ 13 = 18; 𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟 𝑟𝑟𝑟𝑟𝑟𝑟 = 3
Dividend = Divisor x Quotient + Remainder; 13 x 18 + 3 = 237, so it is correct.
NOTE: We can never divide by Zero.
DIVISION PROPERTIES.
• Closure property: The Division in Natural Numbers has NOT Closure Property .
3 ÷ 2 = 1.5 (1.5 is not a Natural Number)
• The Division is NOT Commutative.
𝒂𝒂 ÷ 𝒃𝒃 ≠ 𝒃𝒃 ÷ 𝒂𝒂
𝟑𝟑 ÷ 𝟐𝟐 ≠ 𝟐𝟐 ÷ 𝟑𝟑
• Associative Property: Only when 𝒂𝒂 > 𝒃𝒃 > 𝒄𝒄 𝒂𝒂𝒏𝒏𝒏𝒏 ( 𝒂𝒂 ÷ 𝒃𝒃) > 𝒄𝒄 and with exact
divisions.
𝒂𝒂 ÷ 𝒃𝒃 ÷ 𝒄𝒄 = ( 𝒂𝒂 ÷ 𝒃𝒃) ÷ 𝒄𝒄 = 𝒂𝒂 ÷ (𝒃𝒃 ÷ 𝒄𝒄)
(100 ÷ 4) ÷ 2 = 100 ÷ (4 ÷ 2)
Axel Cotón Gutiérrez Mathematics 4º ESO 0.17

18. Unit 00 September
100 > 4 > 2
• Additive Identity Property: The division of any number by one is that number.
𝒂𝒂 ÷ 𝟏𝟏 = 𝒂𝒂
5 ÷ 1 = 5
MATH VOCABULARY: To Divide, To Share, Inverse, Dividend, Divisor, Quotient,
Remainder, Algorithm.
4.5. COMBINED OPERATIONS.
Look at these expressions: 6 + 2 ∙ 4 and (6 + 2) ∙ 4; although they have the same
numbers and the same operations, their values are different:
6 + 2 ⋅ 4 = 6 + 8 = 14
(6 + 2) ⋅ 4 = 8 ⋅ 4 = 32
When expressions have more than one operation, we have to follow rules for
the order of operations. To remember these rules we will use the BODMAS or
BEDMAS rule:
• B: Brackets. ( ) before [ ].
• O: Orders (Powers). E: Exponents
• D M: Divisions and Multiplications (left to right).
• A S: Additions and Subtractions (left to right).
Example 1:
Solve 3 + 6 𝑥𝑥 (5 + 4) 3 − 7 using the rules for the correct order of operations.
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟏𝟏: 3 + 6 𝑥𝑥 (5 + 4) ÷ 3 − 7 = 3 + 6 𝑥𝑥 9 ÷ 3 − 7 𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵
Axel Cotón Gutiérrez Mathematics 4º ESO 0.18

19. Unit 00 September
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟐𝟐: 3 + 6 𝑥𝑥 9 ÷ 3 − 7 = 3 + 54 ÷ 3 − 7 𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟑𝟑: 3 + 54 ÷ 3 − 7 = 3 + 18 − 7 𝐷𝐷𝐷𝐷𝐷𝐷𝑖𝑖𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟒𝟒: 3 + 18 − 7 = 21 − 7 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟓𝟓: 21 − 7 = 14 𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆
Example 2:
Calculate 9 − 5 ÷ (8 − 3) 𝑥𝑥 2 + 6 using the correct order of operations.
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟏𝟏: 9 − 5 ÷ (8 − 3) 𝑥𝑥 2 + 6 = 9 − 5 ÷ 5 𝑥𝑥 2 + 6 𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟐𝟐: 9 − 5 ÷ 5 𝑥𝑥 2 + 6 = 9 − 1 𝑥𝑥 2 + 6 𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟑𝟑: 9 − 1 𝑥𝑥 2 + 6 = 9 − 2 + 6 𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟒𝟒: 9 − 2 + 6 = 7 + 6 𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆
𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝟓𝟓: 7 + 6 = 13 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴
PROPERTY.
• Distributive Property: says that multiplying a number by a group of numbers
added together is the same as doing each multiplication.
𝒂𝒂 ∙ ( 𝒃𝒃 + 𝒄𝒄) = 𝒂𝒂 ∙ 𝒃𝒃 + 𝒂𝒂 ∙ 𝒄𝒄
𝒂𝒂 ∙ ( 𝒃𝒃 − 𝒄𝒄) = 𝒂𝒂 ∙ 𝒃𝒃 − 𝒂𝒂 ∙ 𝒄𝒄
3 ∙ (2 + 4) = 3 ∙ 2 + 3 ∙ 4
3 ∙ (4 − 2) = 3 ∙ 4 − 3 ∙ 2
MATH VOCABULARY: Combined Operation, Expression, Power, To Solve, To Calculate,
Step, Distributive Property.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.19

20. Unit 00 September
5. WHOLE NUMBER PROBLEMS.
In order to solve problems you must follow the rules below:
• Start with a first reading of the problem to know what it is about.
• Then you do a second reading more slowly, in order to understand the problem
and find out what data it provides.
• Write down the data of the problem clearly. If it is a geometric problem, then
you can make a drawing. You must also check that the units are all the same. If
they are not, then you will have to change them to the appropriate ones.
• Now you can do all the necessary operations to solve the problem.
• Finally, answering: Reread the question of the problem and answer it with a
sentence. Don't forget to mention the correct unit and check that the answer
makes sense.
Example John has 350 euros in his bank account. He has received 37 euros as a
birthday present and then, he has bought 4 DVDs which cost €15 each. How much
money does he have now?
DATA:
Saved: 350 euros
Gift: 37 euros
Spend: 4 x 15 euros
SOLVE:
350 + 37 = 387 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒
4 ∙ 15 = 60 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒
387 − 60 = 327 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒
ANSWER:
John has now 327 euros
MATH VOCABULARY: Geometry, To Draw, Unit, Answer.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.20

21. Unit 00 September
This traditional Japanese game just need two pairs of hands and some strategy
(and simple adding) skills! Good fun for getting kids thinking - and every game ends up
differently! You need at least 2 children, but you can play with more if your adding
skills are up to it!
The object of the game is to be the last player left with a hand in the game. A
hand is "dead" and has to be hidden behind the back when all 5 fingers (or chopsticks)
are extended. Play as follows:
• Players each put one finger out and hold their hands in front of them. One
person starts by using one of his hands to touch any other person's hand. The
person he touches adds up the number of fingers involved (on this first go it
would be two - one on each of the children's hands) and holds that number of
fingers out. Play then passes to the next child (move clockwise around the group,
if there are more than two children).
• When it is your turn, if you have more than 1 finger extended on each hand, you
can choose to touch your own hands together rather than touch someone else's
hand. If you do this, you add together the number of fingers on both hands, then
split that number between your two hands in a different way. So, for example, if
you had 4 fingers extended on your right hand and 2 on your left hand, you
might tap them together then split them so that you have 3 extended on each
hand. Obviously it is a good idea to do this if you have 4 fingers extended on one
hand, because with one more touch that hand could become "dead" and have to
go out of the game. You can't do this if you 4 fingers extended on each hand, or 4
on one hand and 3 on the other, as you would just be swapping your fingers
around indefinitely.
Axel Cotón Gutiérrez Mathematics 4º ESO 0.21