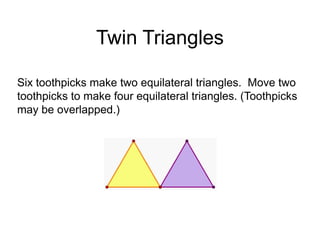
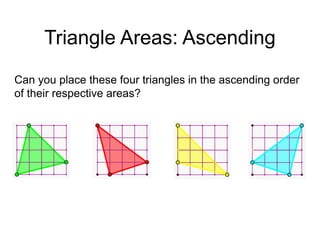
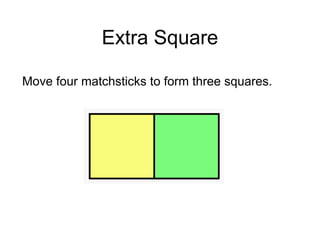
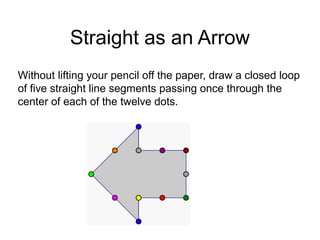
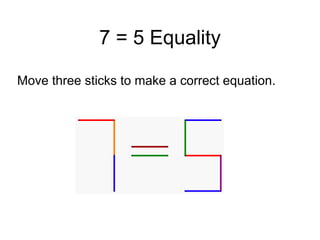
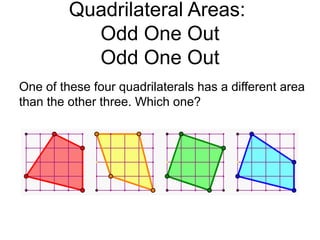
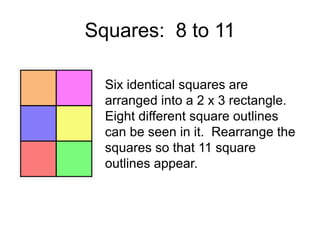
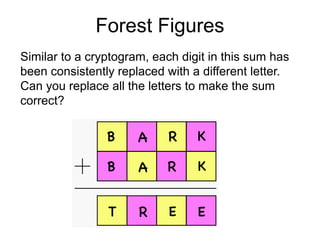
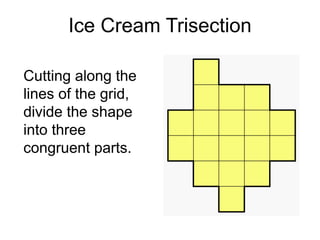
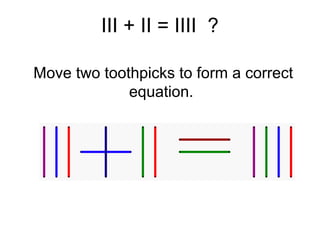
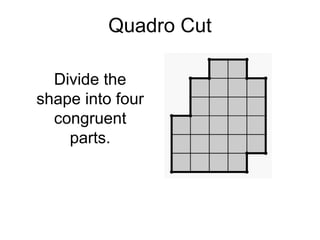
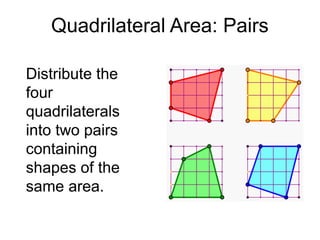
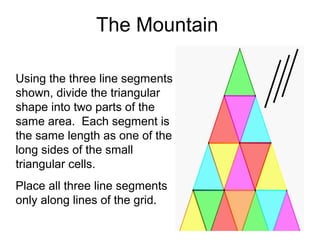
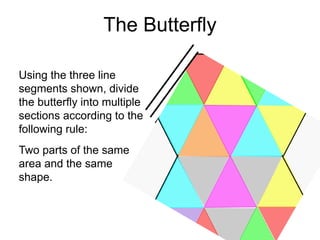
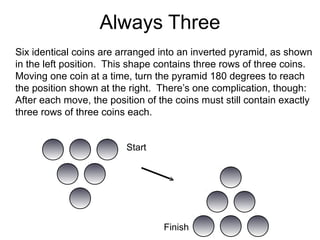
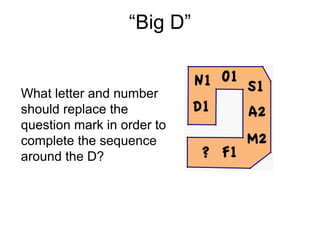
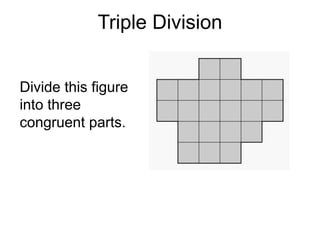
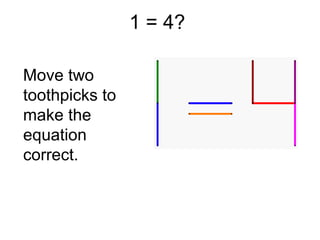
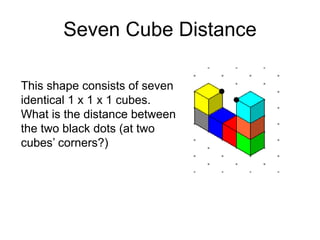
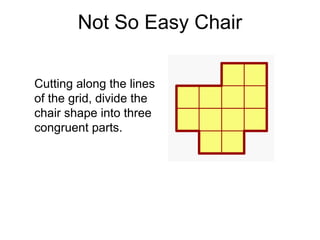
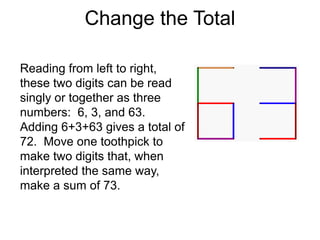
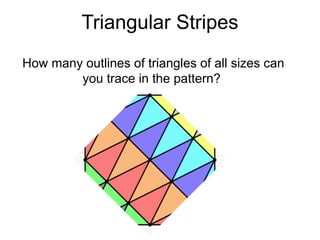
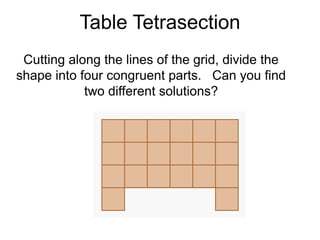
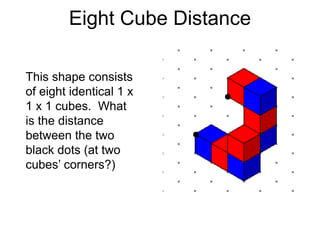
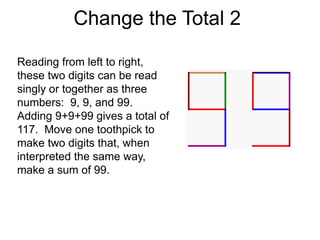
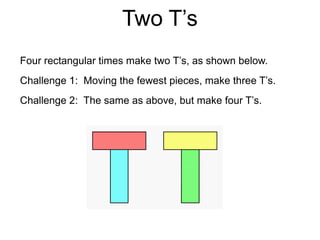
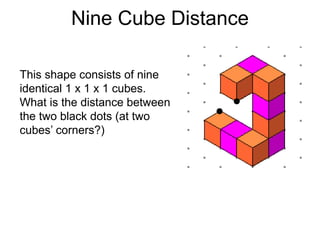
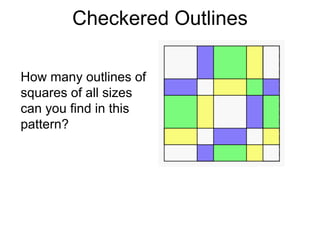
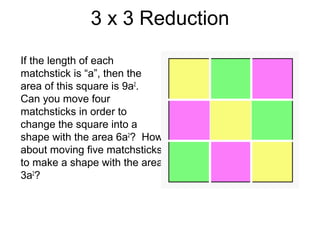
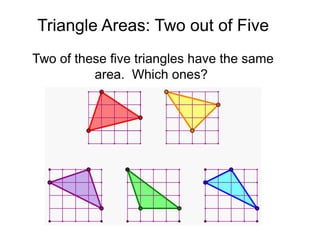
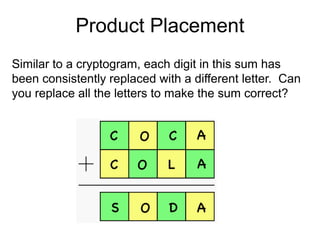
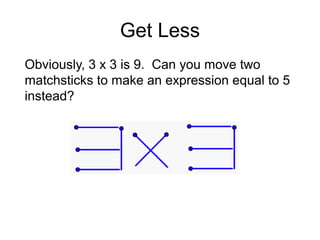
The document presents a series of mathematical puzzles designed to enhance problem-solving skills and encourage perseverance. Each challenge involves finding solutions through various manipulations of shapes, numbers, and patterns, while also fostering creativity and logical thinking. Examples include breaking shapes into congruent parts, rearranging geometrical figures, and solving numerical equations with hints provided.

1. Puzzles and Recreational
Math
Developing Perseverance for
Problem Solving while
Having Fun!

2. Break All Rectangles
Challenge 1: How many rectangles of all possible sizes can
you find in this diagram? Rectangles are found by locating
four dots that lie at the rectangle’s corners.
Challenge 2: What is the least number of stars you must
remove so that no rectangles remain in the diagram?

3. Twin Triangles
Six toothpicks make two equilateral triangles. Move two
toothpicks to make four equilateral triangles. (Toothpicks
may be overlapped.)

4. Triangle Areas: Ascending
Can you place these four triangles in the ascending order
of their respective areas?

5. What’s In The Square?
What should be drawn instead of the question mark in the
empty square to make the pattern complete?

6. Extra Square
Move four matchsticks to form three squares.

7. Straight as an Arrow
Without lifting your pencil off the paper, draw a closed loop
of five straight line segments passing once through the
center of each of the twelve dots.

8. 7 = 5 Equality
Move three sticks to make a correct equation.

9. Flower Petals
Which letters should replace the two question marks
on the flower petals and why?

10. Quadrilateral Areas:
Odd One Out
Odd One Out
One of these four quadrilaterals has a different area
than the other three. Which one?

11. Squares: 8 to 11
Six identical squares are
arranged into a 2 x 3 rectangle.
Eight different square outlines
can be seen in it. Rearrange the
squares so that 11 square
outlines appear.

12. X < X?
Obviously, X cannot be less than itself. Move one
stick to another position to make a correct
statement.

13. Forest Figures
Similar to a cryptogram, each digit in this sum has
been consistently replaced with a different letter.
Can you replace all the letters to make the sum
correct?

14. Ice Cream Trisection
Cutting along the
lines of the grid,
divide the shape
into three
congruent parts.

15. III + II = IIII ?
Move two toothpicks to form a correct
equation.

16. Quadro Cut
Divide the
shape into four
congruent
parts.

17. Quadrilateral Area: Pairs
Distribute the
four
quadrilaterals
into two pairs
containing
shapes of the
same area.

18. The Mountain
Using the three line segments
shown, divide the triangular
shape into two parts of the
same area. Each segment is
the same length as one of the
long sides of the small
triangular cells.
Place all three line segments
only along lines of the grid.

19. Twin Time
You have a 24-hour clock whose display always shows four
digits. That means it displays times from 00:00 (exactly
midnight, or 12:00 AM) to 23:59 (one minute before midnight,
or 11:59 PM).
For the purposes of this puzzle, let’s call a time when the
hours and minutes of the clock display the same time (such
as 12:12) as a “twin time.” How many times during a single
24-hour period will such “twin times” occur?

20. The Butterfly
Using the three line
segments shown, divide
the butterfly into multiple
sections according to the
following rule:
Two parts of the same
area and the same
shape.

21. Always Three
Six identical coins are arranged into an inverted pyramid, as shown
in the left position. This shape contains three rows of three coins.
Moving one coin at a time, turn the pyramid 180 degrees to reach
the position shown at the right. There’s one complication, though:
After each move, the position of the coins must still contain exactly
three rows of three coins each.
Start
Finish

22. “Big D”
What letter and number
should replace the
question mark in order to
complete the sequence
around the D?

23. Triple Division
Divide this figure
into three
congruent parts.

24. 1 = 4?
Move two
toothpicks to
make the
equation
correct.

25. Seven Cube Distance
This shape consists of seven
identical 1 x 1 x 1 cubes.
What is the distance between
the two black dots (at two
cubes’ corners?)

26. Not So Easy Chair
Cutting along the lines
of the grid, divide the
chair shape into three
congruent parts.

27. Change the Total
Reading from left to right,
these two digits can be read
singly or together as three
numbers: 6, 3, and 63.
Adding 6+3+63 gives a total of
72. Move one toothpick to
make two digits that, when
interpreted the same way,
make a sum of 73.

28. Triangular Stripes
How many outlines of triangles of all sizes can
you trace in the pattern?

29. Choco-break
Break the chocolate bar into
four congruent pieces. Each
break must be made along a
single straight line running
from edge to edge of the bar or
an already separated
fragment.

30. Ad Algebra
One day an webmaster logged in to look at
4
5
the ad revenues from his site. His account
showed, “Today’s Earnings” as $0.01,
“Yesterday’s Earnings” as $1.33, and “This
2
Month’s Earnings” as X. 8
The very next day the webmaster logged on
1
0
once again. This time, “Today’s Earnings”
was $0.04, while “Yesterday’s Earnings” was
$1.51, and “This Month’s Earnings” was now 3
9
$9.69. Given that both days were in the
same month, can you determine the value of
X?
6

31. Table Tetrasection
Cutting along the lines of the grid, divide the
shape into four congruent parts. Can you find
two different solutions?

32. Increasing Time
You have a 24-hour clock whose display always shows four
digits. That means it displays times from 00:00 (exactly
midnight, or 12:00 AM) to 23:59 (one minute before midnight,
or 11:59 PM).
For the purposes of this puzzle, let’s call a time when the
clock displays four digits that make an increasing arithmetic
progression (such as 12:34) with an increasing constant of 1
an “increasing time.” How many times during a single 24-
hour period will such “increasing times” occur?

33. Eight Cube Distance
This shape consists
of eight identical 1 x
1 x 1 cubes. What
is the distance
between the two
black dots (at two
cubes’ corners?)

34. Change the Total 2
Reading from left to right,
these two digits can be read
singly or together as three
numbers: 9, 9, and 99.
Adding 9+9+99 gives a total of
117. Move one toothpick to
make two digits that, when
interpreted the same way,
make a sum of 99.

35. Letter Relations
What letter should replace the question mark
in order to logically complete the complex
equation?
E D N ?
R S U W

36. Two T’s
Four rectangular times make two T’s, as shown below.
Challenge 1: Moving the fewest pieces, make three T’s.
Challenge 2: The same as above, but make four T’s.

37. Nine Cube Distance
This shape consists of nine
identical 1 x 1 x 1 cubes.
What is the distance between
the two black dots (at two
cubes’ corners?)

38. Checkered Outlines
How many outlines of
squares of all sizes
can you find in this
pattern?

39. 3 x 3 Reduction
If the length of each
matchstick is “a”, then the
area of this square is 9a2.
Can you move four
matchsticks in order to
change the square into a
shape with the area 6a2? How
about moving five matchsticks
to make a shape with the area
3a2?

40. Triangle Areas: Two out of Five
Two of these five triangles have the same
area. Which ones?

41. 23 versus 32
The two missing digits in this sequence are 2 and 3. (For
now, their places are being held by question marks). But
don’t write them in just yet! We haven’t told you in what
order they should go. Should the first question mark be
replaced with 2 and the second one with 3, or vice versa?
8, 5, 4, 9, 1, 7, 6, ?, ?

42. Product Placement
Similar to a cryptogram, each digit in this sum has
been consistently replaced with a different letter. Can
you replace all the letters to make the sum correct?

43. Get Less
Obviously, 3 x 3 is 9. Can you move two
matchsticks to make an expression equal to 5
instead?

44. Coin Cup
Eight coins are arranged in the shape of a
cup. Move two coins to new positions to turn
the cup upside down.