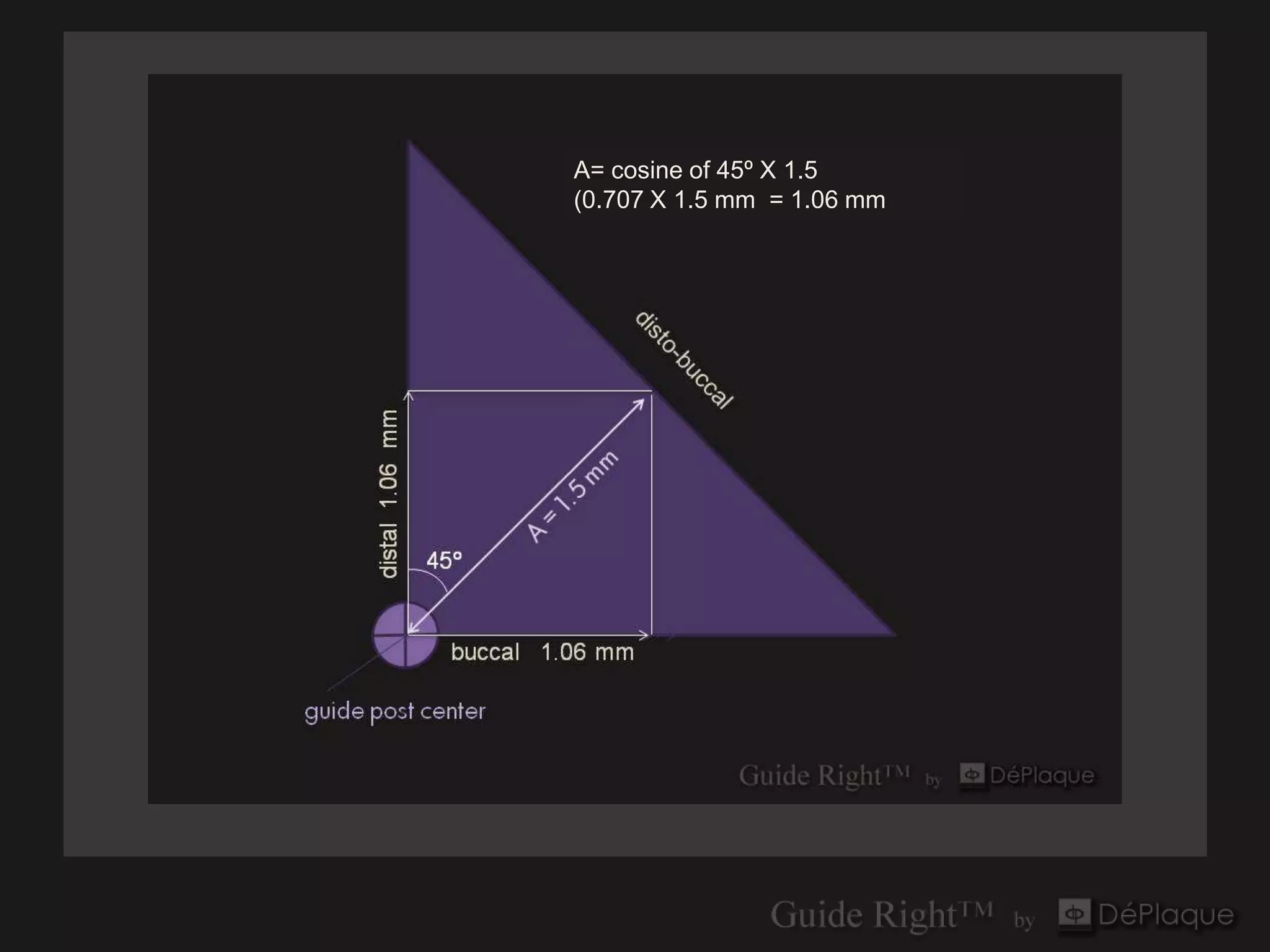
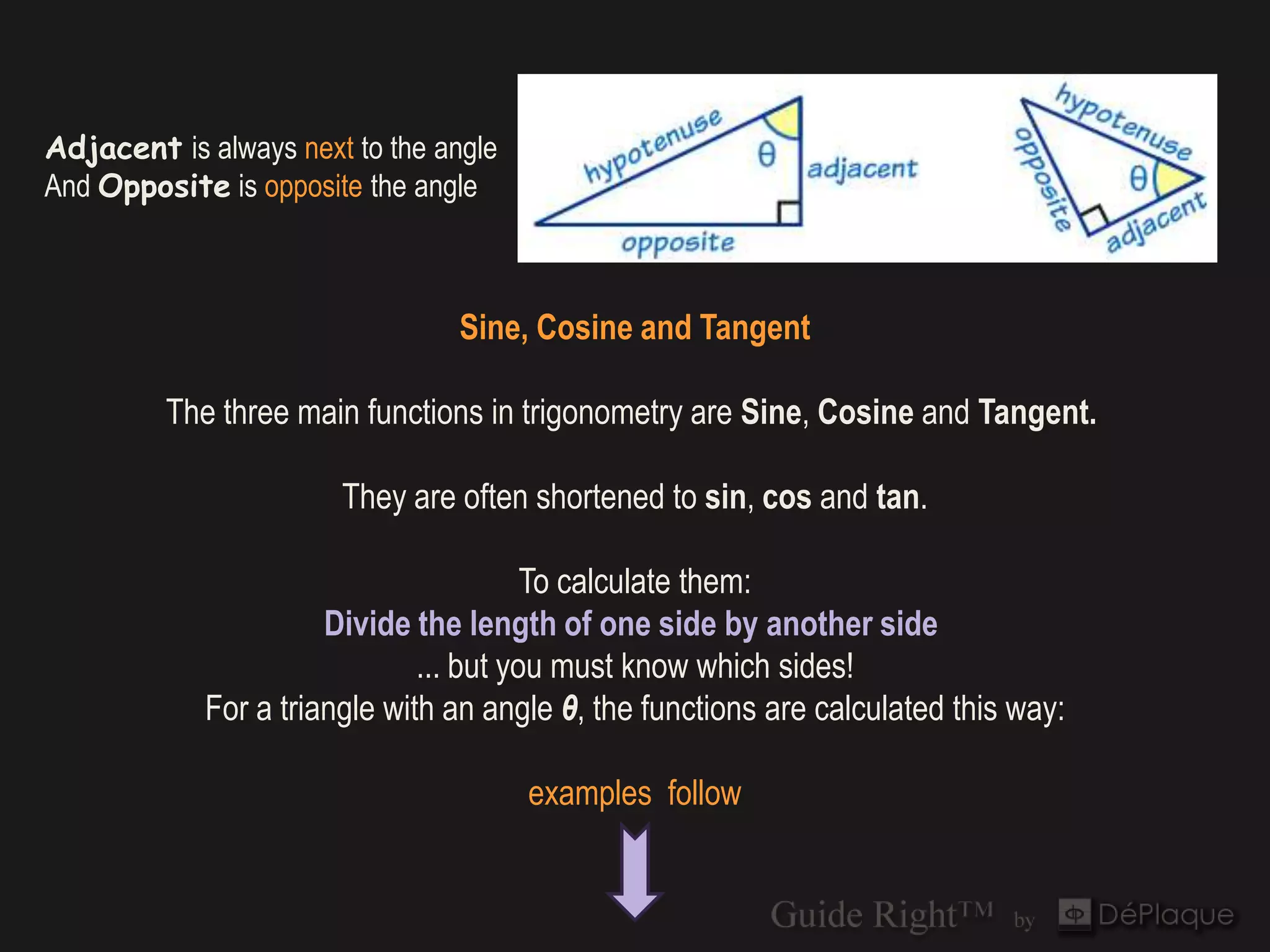
The document discusses the application of the Pythagorean theorem and cosine calculations in surgical guide design, particularly for guide right corrections at a 45° angle. It provides formulas for calculating sine, cosine, and tangent functions in relation to right triangles, using various examples to illustrate these concepts. Additionally, it emphasizes the importance of correctly identifying triangle sides when performing these calculations.

1. DéPlaque
Pythagorean Theorem
COSINE Calculations for Guide Right™ Guides
The cosine of 45°
is recommended for Guide Right corrections
BECAUSE
rotating the offset guide post half way
between 2 adjacent planes (90° apart) is 45°.
2.2013

2. Correction based on the calculations
from the Pythagorean Theorem
To move the position of the guide sleeve 1.4 mm both mesially & buccally:
► use a 3 mm X 1.5 mm offset guide post
► and direct the offset 45º facially and buccally.
Cosine: 1.5 mm X 0.71 = 1.06 mm
see Powerpoint > Use of Pythagorean Theorem
in # 9 Single Implant Case

3. A= cosine of 45º X 1.5
(0.707 X 1.5 mm = 1.06 mm

4. SOHCAHTOA
A way of remembering how to compute the sine, cosine, and tangent of an angle.
SOH stands for Sine equals Opposite over Hypotenuse.
CAH stands for Cosine equals Adjacent over Hypotenuse.
TOA stands for Tangent equals Opposite over Adjacent.
SOH sin θ = _opposite_
hypotenuse
hypotenuse
CAH cos θ = _adjacent_ opposite side
hypotenuse
θ
TOA tan θ = _opposite_
adjacent adjacent side

5. 3
EXAMPLE
Find the values of sin θ, cos θ, and tan θ
in the right triangle shown. 4
5
θ
3 opposite side
ANSWER
sin θ = 3/5 = 0.6
adjacent side
cosθ = 4/5 = 0.8
tanθ = 3/4 = 0.75 4
5
This triangle is oriented differently than the θ
one shown in the SOHCAHTOA diagram,
so make sure you know which sides are
the opposite, adjacent, and hypotenuse.

6. How is basic COSINE calculated?
Sine, Cosine and Tangent
Three Functions, but same idea.
Right Triangle
Sine, Cosine and Tangent are all based on a Right-Angled Triangle
opposite side
θ
adjacent side

7. Adjacent is always next to the angle
And Opposite is opposite the angle
Sine, Cosine and Tangent
The three main functions in trigonometry are Sine, Cosine and Tangent.
They are often shortened to sin, cos and tan.
To calculate them:
Divide the length of one side by another side
... but you must know which sides!
For a triangle with an angle θ, the functions are calculated this way:
examples follow

8. Example:
What is the sine of 35°?
Sine Function: sin(θ) = Opposite / Hypotenuse
Cosine Function: cos(θ) = Adjacent / Hypotenuse
Tangent Function: tan(θ) = Opposite / Adjacent
Using this triangle (lengths are only to one decimal place):
sin(35°) = Opposite / Hypotenuse =
2.8 / 4.9 = 0.57...
Good calculators have sin, cos and tan on them,
to make it easy for you.
Just put in the angle and press the button.
But you still need to remember what they mean!

9. Example:
What are the sine, cosine and tangent of 45° ?
Used in Guide Right™ Surgical guide calculations
The classic 45° triangle has two sides of 1 and a hypotenuse of √(2
Sine sin(45°) = 1 / 1.414 = 0.707
Cosine cos(45°) = 1 / 1.414 = 0.707
Tangent tan(45°) = 1 / 1 = 1
http://www.mathsisfun.com/sine-cosine-tangent.html