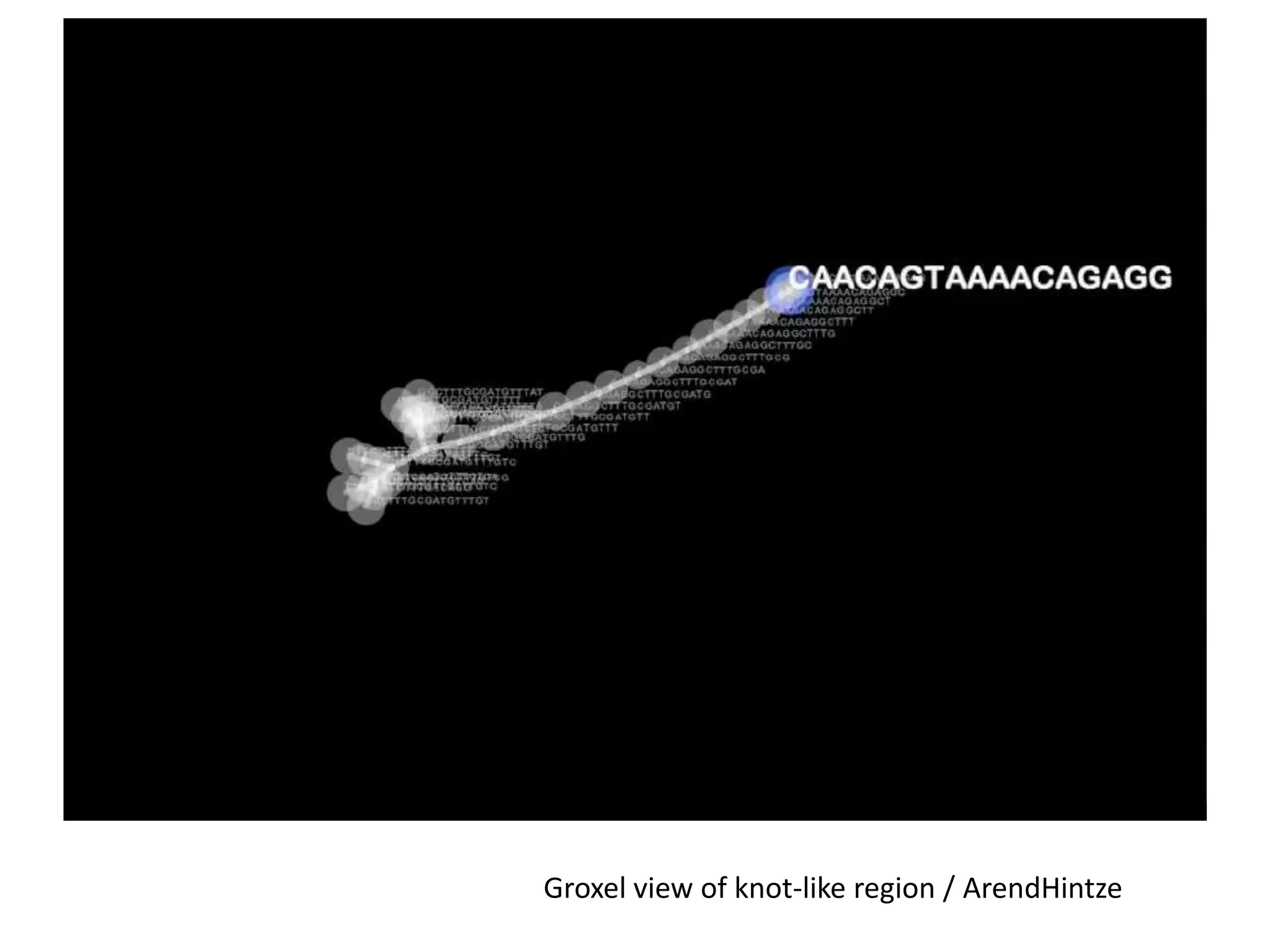
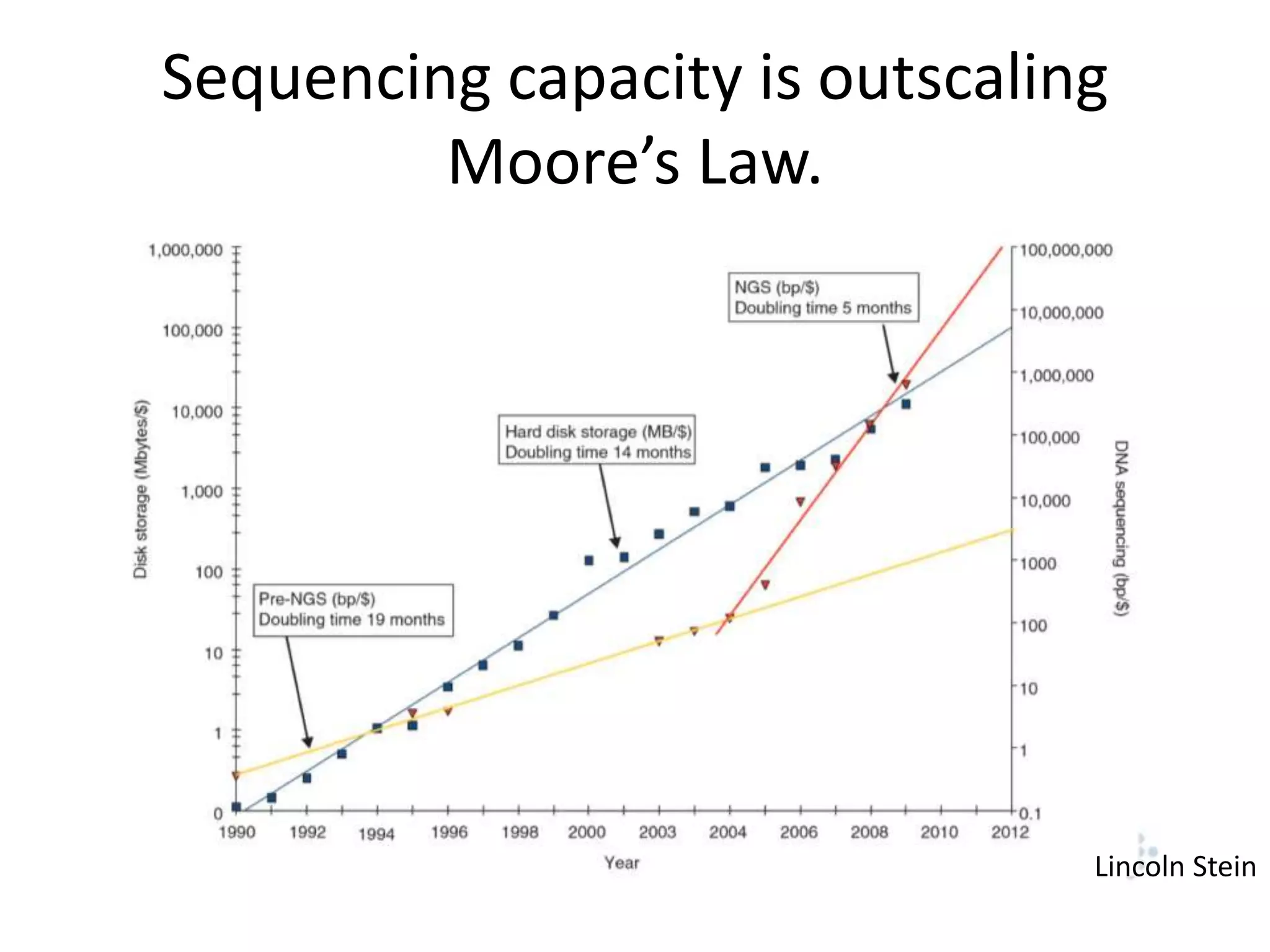
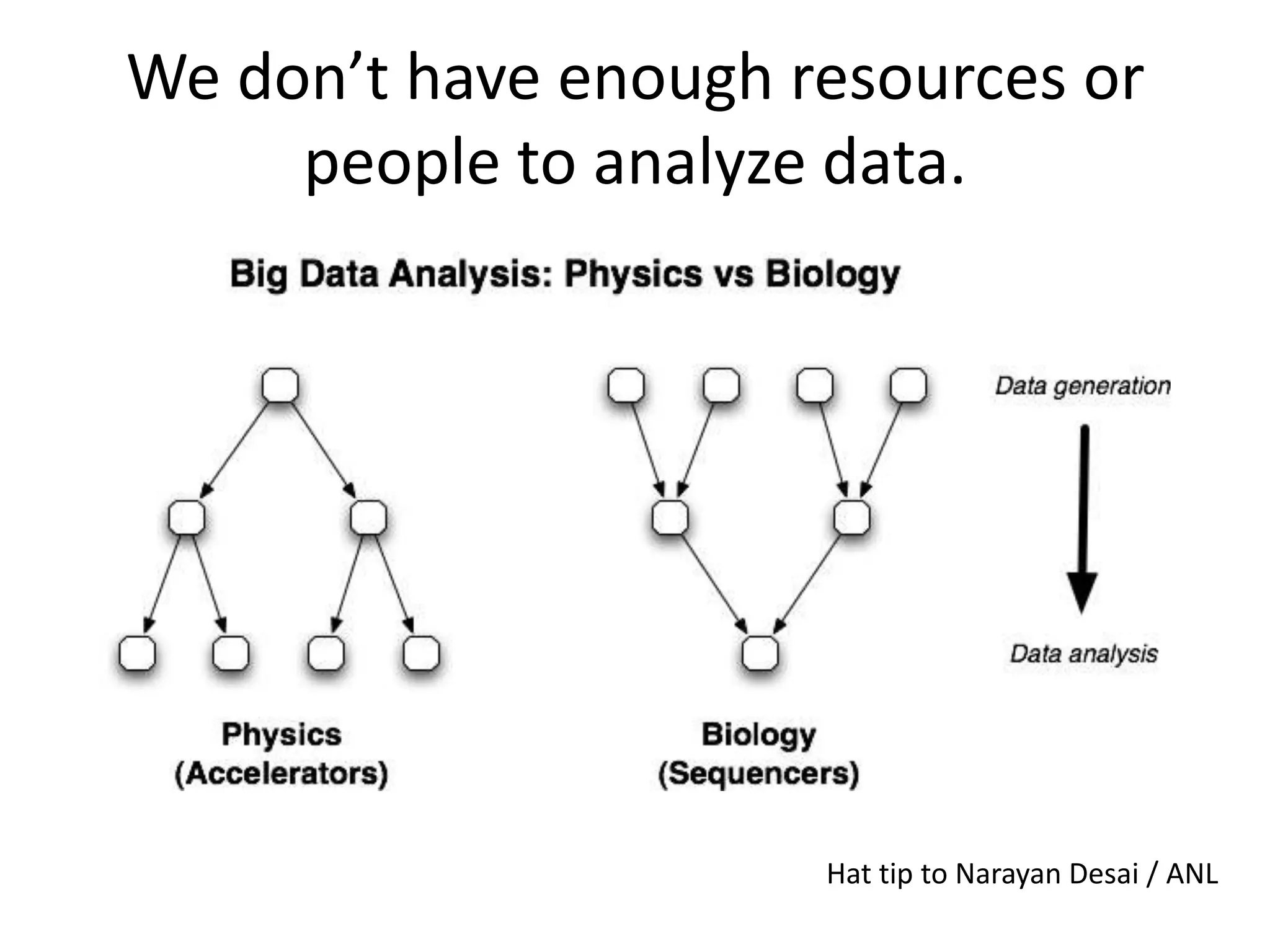
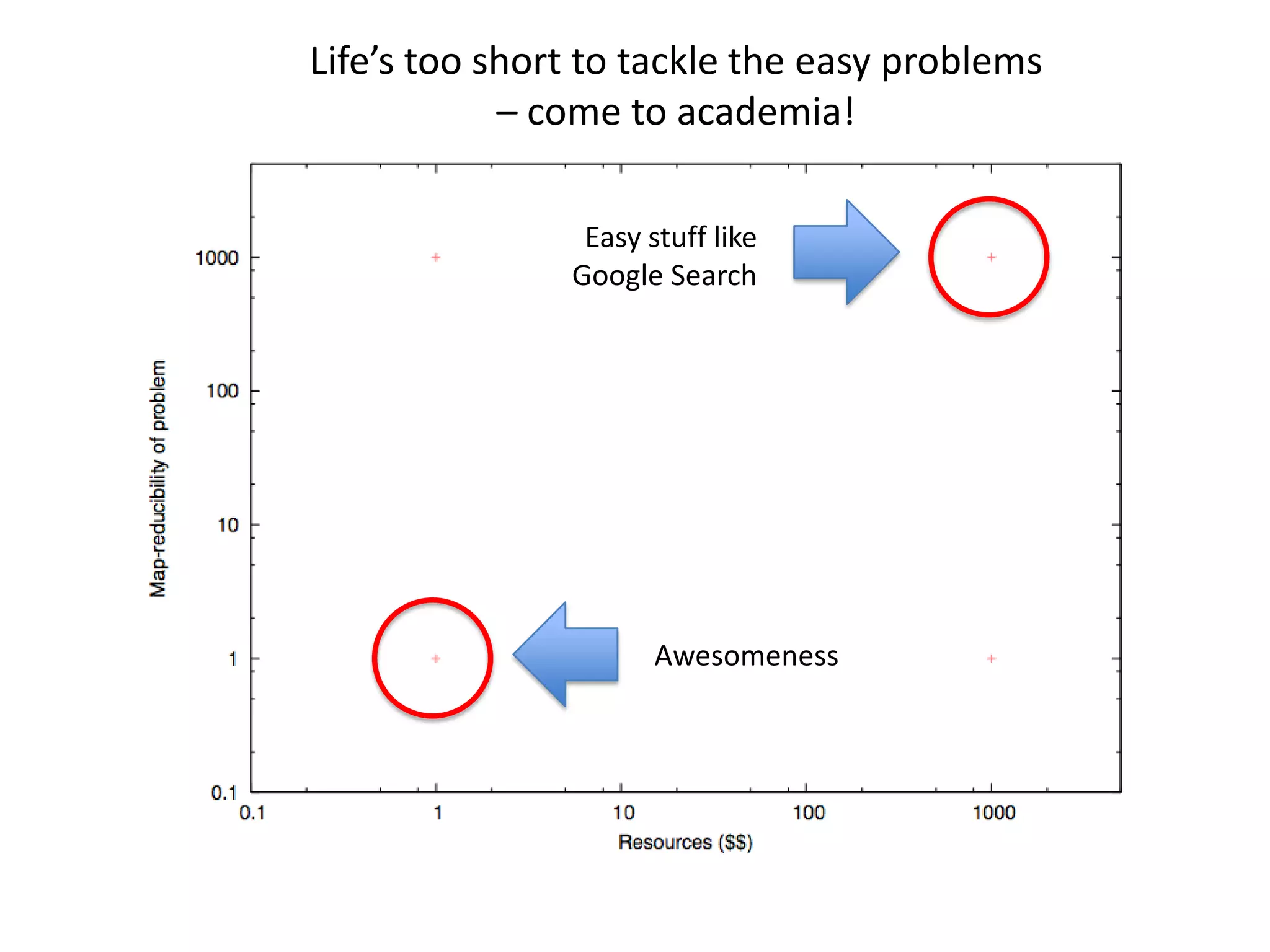
This document summarizes a talk about using probabilistic data structures like Bloom filters to handle large genomic and sequencing datasets. Bloom filters allow storing and querying enormous numbers of DNA fragments and sequences in a way that is memory efficient and scales to very large datasets. The talk describes how Bloom filters can be used to assemble genomes and reduce complexity in assembly graphs. While not perfect representations, Bloom filters enable genomic assembly and analysis that would otherwise not be possible given the volume of data.

2. Handling ridiculous amounts of data with probabilistic data structuresC. Titus BrownMichigan State UniversityComputer Science / Microbiology

3. Resourceshttp://www.slideshare.net/c.titus.brown/Webinar: http://oreillynet.com/pub/e/1784Source: github.com/ctb/N-grams (this talk): khmer-ngramDNA (the real cheese): khmerkhmer is implemented in C++ with a Python wrapper, which has been awesome for scripting, testing, and general development. (But man, does C++ suck…)

4. Lincoln SteinSequencing capacity is outscaling Moore’s Law.

5. Hat tip to Narayan Desai / ANLWe don’t have enough resources or people to analyze data.

6. Data generation vs data analysisIt now costs about $10,000 to generate a 200 GB sequencing data set (DNA) in about a week. (Think: resequencing human; sequencing expressed genes; sequencing metagenomes, etc.) …x1000 sequencersMany useful analyses do not scale linearly in RAM or CPU with the amount of data.

7. The challenge?Massive (and increasing) data generation capacity, operating at a boutique level, with algorithms that are wholly incapable of scaling to the data volume.Note: cloud computing isn’t a solution to a sustained scaling problem!! (See: Moore’s Law slide)

8. Life’s too short to tackle the easy problems – come to academia!Easy stuff like Google SearchAwesomeness

9. A brief intro to shotgun assemblyIt was the best of times, it was the wor, it was the worst of times, it was the isdom, it was the age of foolishnessmes, it was the age of wisdom, it was thIt was the best of times, it was the worst of times, it was the age of wisdom, it was the age of foolishness…but for 2 bn+ fragments.Not subdivisible; not easy to distribute; memory intensive.

10. Define a hash function (word => num)def hash(word): assert len(word) <= MAX_K value = 0 for n, ch in enumerate(word): value += ord(ch) * 128**n return value

11. class BloomFilter(object): def __init__(self, tablesizes, k=DEFAULT_K):self.tables = [ (size, [0] * size) \ for size in tablesizes ]self.k = k def add(self, word): # insert; ignore collisionsval = hash(word) for size, ht in self.tables:ht[val % size] = 1 def __contains__(self, word):val = hash(word) return all( ht[val % size] \ for (size, ht) in self.tables )

12. class BloomFilter(object): def __init__(self, tablesizes, k=DEFAULT_K):self.tables = [ (size, [0] * size) \ for size in tablesizes ]self.k = k def add(self, word): # insert; ignore collisionsval = hash(word) for size, ht in self.tables:ht[val % size] = 1 def __contains__(self, word):val = hash(word) return all( ht[val % size] \ for (size, ht) in self.tables )

13. class BloomFilter(object): def __init__(self, tablesizes, k=DEFAULT_K):self.tables = [ (size, [0] * size) \ for size in tablesizes ]self.k = k def add(self, word): # insert; ignore collisionsval = hash(word) for size, ht in self.tables:ht[val % size] = 1 def __contains__(self, word):val = hash(word) return all( ht[val % size] \ for (size, ht) in self.tables )

14. Storing words in a Bloom filter>>> x = BloomFilter([1001, 1003, 1005])>>> 'oogaboog' in xFalse>>> x.add('oogaboog')>>> 'oogaboog' in xTrue>>> x = BloomFilter([2]) >>> x.add('a')>>> 'a' in x # no false negativesTrue>>> 'b' in xFalse>>> 'c' in x # …but false positivesTrue

15. Storing words in a Bloom filter>>> x = BloomFilter([1001, 1003, 1005])>>> 'oogaboog' in xFalse>>> x.add('oogaboog')>>> 'oogaboog' in xTrue>>> x = BloomFilter([2]) # …false positives>>> x.add('a')>>> 'a' in xTrue>>> 'b' in xFalse>>> 'c' in xTrue

16. Storing text in a Bloom filterclass BloomFilter(object): … def insert_text(self, text): for i in range(len(text)-self.k+1):self.add(text[i:i+self.k])

17. def next_words(bf, word): # try all 1-ch extensions prefix = word[1:] for ch in bf.allchars: word = prefix + ch if word in bf: yield ch# descend into all successive 1-ch extensionsdef retrieve_all_sentences(bf, start): word = start[-bf.k:]n = -1 for n, ch in enumerate(next_words(bf, word)):ss = retrieve_all_sentences(bf,start + ch) for sentence in ss: yield sentence if n < 0: yield start

18. def next_words(bf, word): # try all 1-ch extensions prefix = word[1:] for ch in bf.allchars: word = prefix + ch if word in bf: yield ch# descend into all successive 1-ch extensionsdef retrieve_all_sentences(bf, start): word = start[-bf.k:]n = -1 for n, ch in enumerate(next_words(bf, word)):ss = retrieve_all_sentences(bf,start + ch) for sentence in ss: yield sentence if n < 0: yield start

19. Storing and retrieving text>>> x = BloomFilter([1001, 1003, 1005, 1007])>>> x.insert_text('foo bar bazbif zap!')>>> x.insert_text('the quick brown fox jumped over the lazy dog')>>> print retrieve_first_sentence(x, 'foo bar ')foo bar bazbif zap!>>> print retrieve_first_sentence(x, 'the quic')the quick brown fox jumped over the lazy dog

20. Sequence assembly>>> x = BloomFilter([1001, 1003, 1005, 1007])>>> x.insert_text('the quick brown fox jumped ')>>> x.insert_text('jumped over the lazy dog')>>> retrieve_first_sentence(x, 'the quic')the quick brown fox jumpedover the lazy dog(This is known as the de Bruin graph approach to assembly; c.f. Velvet, ABySS, SOAPdenovo)

21. Repetitive strings are the devil>>> x = BloomFilter([1001, 1003, 1005, 1007])>>> x.insert_text('nanana, batman!')>>> x.insert_text('my chemical romance: nanana')>>> retrieve_first_sentence(x, "my chemical")'my chemical romance: nanana, batman!'

22. Note, it’s a probabilistic data structureRetrieval errors:>>> x = BloomFilter([1001, 1003]) # small Bloom filter…>>> x.insert_text('the quick brown fox jumped over the lazy dog’)>>> retrieve_first_sentence(x, 'the quic'),('the quick brY',)

23. Assembling DNA sequenceCan’t directly assemble with Bloom filter approach (false connections, and also lacking many convenient graph properties)But we can use the data structure to grok graph properties and eliminate/break up data:Eliminate small graphs (no false negatives!)Disconnected partitions (parts -> map reduce)Local graph complexity reduction & error/artifact trimming…and then feed into other programs.This is a data reducing prefilter

24. Right, but does it work??Can assemble ~200 GB of metagenome DNA on a single 4xlarge EC2 node (68 GB of RAM) in 1 week ($500).…compare with not at allon a 512 GB RAM machine.Error/repeat trimming on a tricky worm genome: reduction from170 GB resident / 60 hrs54 GB resident / 13 hrs

25. How good is this graph representation?V. low false positive rates at ~2 bytes/k-mer;Nearly exact human genome graph in ~5 GB.Estimate we eventually need to store/traverse 50 billion k-mers (soil metagenome)Good failure mode: it’s all connected, Jim! (No loss of connections => good prefilter)Did I mention it’s constant memory? And independent of word size?…only works for de Bruijn graphs 

26. Thoughts for the futureUnless your algorithm scales sub-linearly as you distribute it across multiple nodes (hah!), oryour problem size has an upper bound, cloud computing isn’t a long-term solution in bioinformaticsSynopsis data structures & algorithms (which incl. probabilistic data structures) are a neat approach to parsing problem structure.Scalable in-memory local graph exploration enables many other tricks, including near-optimal multinode graph distribution.

27. Groxel view of knot-like region / ArendHintze

28. Acknowledgements:The k-mer gang:Adina HoweJason PellRosangelaCanino-KoningQingpeng ZhangArendHintzeCollaborators:Jim Tiedje (Il padrino)Janet Jansson, Rachel Mackelprang, Regina Lamendella, Susannah Tringe, and many others (JGI)Charles Ofria (MSU)Funding: USDA NIFA; MSU, startup and iCER; DOE; BEACON/NSF STC; Amazon Education.